2. 鲁东大学港口海岸防灾减灾研究院,山东烟台 264025
2. Institute of Port and Coastal Disaster Prevention and Mitigation, Ludong University, Yantai, Shandong, 264025, China
铁山港作为广西北部湾经济区中转运输枢纽港区,是我国西南地区便捷的出海通道,也是我国与东盟国家海上贸易的重要口岸,具有优越的区位优势。为满足铁山港湾内船舶通行和临港工业快速发展的需求,北海市在铁山港区3.5万吨级进港航道基础上拓宽浚深,总长约23.6 km,分10万吨级、5万吨级、1万吨级和5 000吨级4段进行设计。由于施工情况复杂等因素,目前仅完成Ⅰ、Ⅱ标段。Ⅲ标段东侧多生长有红树林,红树林生态系统具有丰富的生物多样性和极高的生产力,同时发挥着诸多其他生态系统所不能替代的重要功能,研究Ⅲ标段疏浚工程引起的水动力改变对周围红树林的影响具有重要意义。水动力环境变化通常通过模型来模拟。辛文杰[1]、陈波等[2]通过数值模拟建立铁山港的潮流模型;施华斌等[3]利用二维浅水模型建立广西沿海的水动力模型,分析河流对近岸水动力的影响;王丽娜等[4]利用三维浅海水动力模型建立潮流场模型;李小维等[5]、Yang等[6]通过历史数据和数值模型研究铁山港的水动力特征;谢洁[7]利用数值模型研究铁山港的潮流和泥沙输运,计算得到规划港区和航道的泥沙回淤强度及回淤总量。随着铁山港航道工程的建设发展,其Ⅲ标段疏浚工程会对周边海域的水动力产生一定影响,而水动力环境是泥沙输运、海洋生态环境变化的动力学基础[8],确定水动力环境变化对铁山港海域环境保护、制定发展规划具有一定参考意义。因此,本研究基于MIKE数值模型,同时为使模型计算更加稳定、输出结果更加精确,在光滩和红树林区域采用不同的曼宁系数[9, 10],详细分析铁山港航道Ⅲ标段疏浚工程引起的航道及红树林区域水动力改变情况,为相关建设和规划制定提供参考。
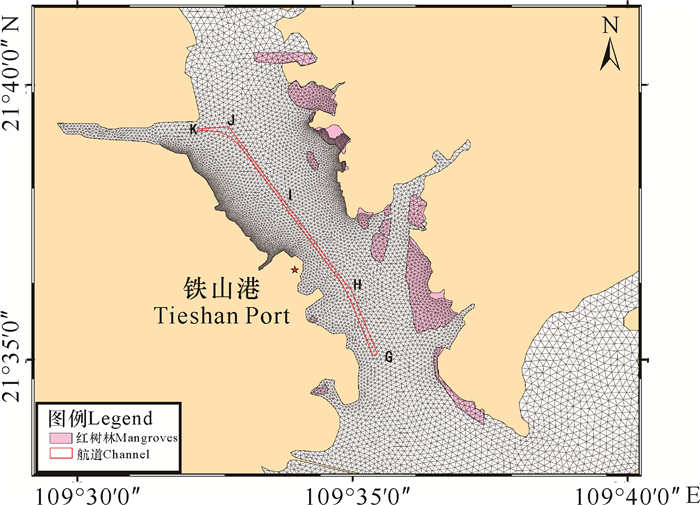
1 材料与方法 1.1 铁山港航道Ⅲ标段疏浚工程北海铁山港航道三期工程Ⅲ标段位于北海铁山港区石头埠作业区至雷田作业区以东海域,起点为三期航道工程设计G点,终点为雷田作业区口门处K点,各标段详细信息见图 1和表 1。北海港铁山港区航道Ⅲ标段疏浚工程施工总工期约12个月,拟疏浚航道总长约9.78 km。全航段采用8 m3(北段)和13 m3(南段)抓斗挖泥船配泥驳开挖,由抓斗船和泥驳清礁,总疏浚量约为3.869 3×106 m3,炸礁量约为3.657×105 m3。
|
| 图 1 工程区域位置及精细化计算网格 Fig. 1 Project area location and fine calculation grid |
| 航段 Channel section |
长度(km) Length(km) |
宽度(m) Width(m) |
通航深度(m) Navigable depth (m) |
底标高(m) Bottom elevation (m) |
| GH | 2.19 | 150 | 11.8 | -12.2 |
| HI | 3.21 | 95 | 7.1 | -7.5 |
| IJ | 3.43 | 75 | 6.1 | -6.5 |
| JK | 0.95 | 75 | 6.1 | -6.5 |
| 合计Total | 9.78 |
工程区附近植物主要为红树植物。在低潮潮位附近分布的红树植物有白骨壤Avicennia marina,高潮潮位附近分布有桐花树Aegiceras corniculatum、卤蕨Acrostichum aureum、老鼠簕Acanthus ilicifolius和半红树植物如黄槿Hibiscus tiliaceus、苦郎树Clerodendrum inerme,岸边一带生长有厚藤Ipomoea pes-caprae、海马齿Sesuvium portulacastrum、南方碱蓬Suaeda australis等。根据周边其他近岸工程调查可知,铁山港附近海域外源性高岭土在红树林区域的堆积和黏附会妨害白骨壤的呼吸及光合作用,导致白骨壤死亡[11, 12]。高岭土的悬沙浓度除了与泥沙源强相关外,海洋水动力环境也对泥沙浓度有着重要影响,因此研究疏浚工程造成的水动力环境改变,对红树林保护具有间接参考价值[13]。
1.2 模型的建立 1.2.1 模型介绍采用平面二维数值模型MIKE21研究目标海域的潮流场。MIKE21采用标准Galerkin有限元法进行水平空间离散,采用显式迎风差分格式离散动量方程与输运方程[14]研究工程造成的泥沙冲淤状况。
连续方程:
| $ \frac{\partial \zeta}{\partial t}+\frac{\partial h u}{\partial x}+\frac{\partial h v}{\partial y}=0, $ | (1) |
向动量方程:
| $ \begin{array}{r} \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}-f v=-g \frac{\partial \zeta}{\partial x}- \\ \frac{g u \sqrt{u^{2}+v^{2}}}{c^{2} h}+\frac{\partial}{\partial x}\left(N_{x} \frac{\partial u}{\partial x}\right)+\frac{\partial}{\partial y}\left(N_{y} \frac{\partial u}{\partial y}\right), \end{array} $ | (2) |
向动量方程:
| $ \begin{gathered} \frac{\partial v}{\partial t}+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}+f u=-g \frac{\partial \zeta}{\partial x}- \\ \frac{g v \sqrt{u^{2}+v^{2}}}{c^{2} h}+\frac{\partial}{\partial x}\left(N_{x} \frac{\partial v}{\partial x}\right)+\frac{\partial}{\partial y}\left(N_{y} \frac{\partial v}{\partial y}\right), \end{gathered} $ | (3) |
式中:t为时间(s);x, y为原点0置于某一水平基面的直角坐标系坐标;u、v分别为流速矢量V沿x、y方向的分量(m/s);ζ为相对于xy坐标平面的水位(m);h=d+ζ,为总水深(m);d为相对于xy坐标平面的水深(m);Nx、Ny分别为x、y向水流紊动黏性系数(m2/s);f为科氏参量(deg);g为重力加速度(m/s2);c=Mh1/6,为谢才系数;M为曼宁糙率系数。
1.2.2 初始条件| $ \begin{aligned} &\left.\zeta(x, y, t)\right|_{t=0}=\zeta_{0}(x, y), \\ &\left.u(x, y, t)\right|_{t=0}=u_{0}(x, y), \\ &\left.v(x, y, t)\right|_{t=0}=v_{0}(x, y), \end{aligned} $ | (4) |
式中:ζ0、u0、v0分别为ζ、u、v的初始值。
1.2.3 边界条件流速法向量为0:
| $ \mathit{\boldsymbol{V}} \cdot \mathit{\boldsymbol{n}} = 0, $ | (5) |
式中: n为固边界法向单位矢量。
开边界水位ζ和流速V可采用已知水位ζ*(x, y, t)或流速V* (x, y, t)控制:
| $ \left.\zeta(x, y, t)\right|_{\Gamma}=\zeta^{*}(x, y, t) \text { (水位) }, $ | (6) |
| $ \left.\boldsymbol{V}(x, y, t)\right|_{\Gamma}=\boldsymbol{V}^{*}(x, y, t)(\text { 流速 })。$ | (7) |
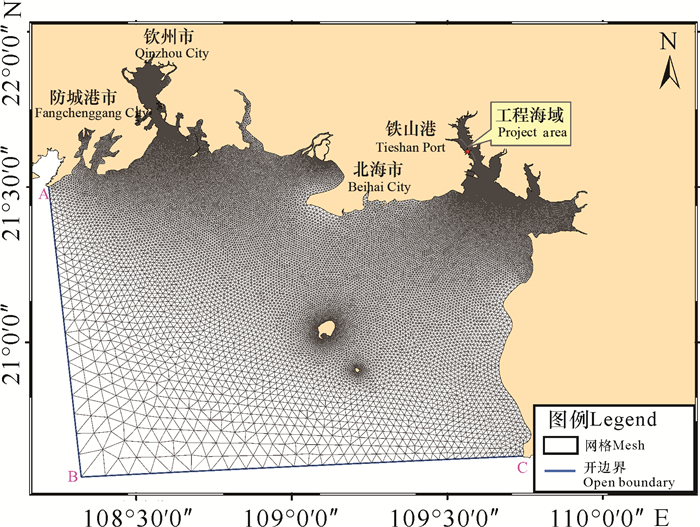
本研究计算区域如图 2所示。铁山港附近海域岛屿众多,岸线曲折,两岸有较多红树林分布。因此采用非结构三角形网格可以较好地贴合自然岸线,提高计算精度和计算效率,并便于各种工程情况的准确布置。用动边界的方法对干、湿网格进行处理,在疏浚工程区附近进行网格加密。计算空间步长在工程海域精确到10 m,网格单元74 004个,网格节点39 307个。
|
| A、B和C分别代表计算区域的起点、拐点和终点 A, B and C represent the starting point, inflection point and end point of the calculation area, respectively 图 2 大区域计算网格分布 Fig. 2 Grid distribution of large area calculation |
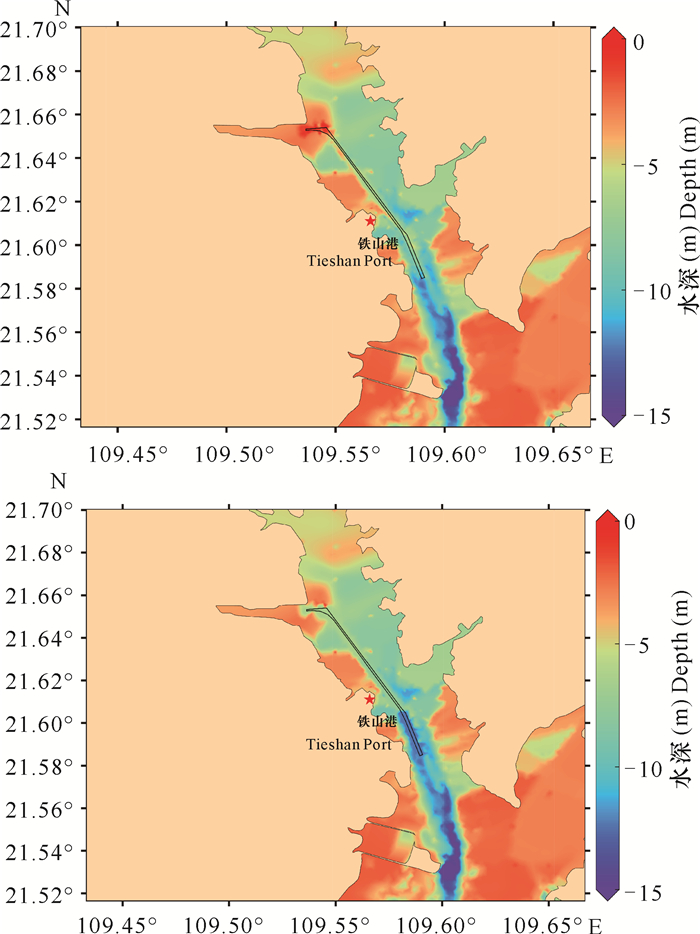
工程附近的海域水深数据来自于中国人民解放军海军司令部航海保证部制作的海图数据(C1416710铁山港及附近)以及航道附近测量的水深数据。对于外海水深,本项目采用美国国家地学测量中心提供的DBDB5 (Digital Bathymetric Database Version 5.2)(https://shoreline.noaa.gov/data/datasheets/wvs.html)原始数据集,通过双线性插值方法插值到网格点上,工程前后水深见图 3。
|
| 图 3 航道及附近海域疏浚工程前(上)后(下)水深分布 Fig. 3 Water depth distribution before (up) and after (down) dredging of the channel and adjacent waters |
潮汐在开边界的振幅、迟角和潮流流速等要素利用MATLAB中的T_tide工具包[15]获得,采用M2、S2、N2、K2、K1、O1、P1、Q1 8个主要分潮。模型计算时间为2021年4月1-23日,合计23 d,计算步长根据Courant-Friedrich Levy (CFL) number笛卡尔坐标下的浅水方程式进行动态调整,确保模型计算稳定。最大时间步长为120 s,最小时间步长0.1 s。底床糙率通过曼宁系数进行控制。因为红树林的高度和分布密度等因素显著改变底床糙率,为准确刻画红树林区域的流场时空分布,底床糙率通过空间变化的曼宁系数所形成的曼宁系数场进行控制。根据倪海祥等[16]的研究及MIKE21中曼宁数定义,光滩曼宁系数设置为林地的10倍,因此本次计算曼宁系数n取4-40。
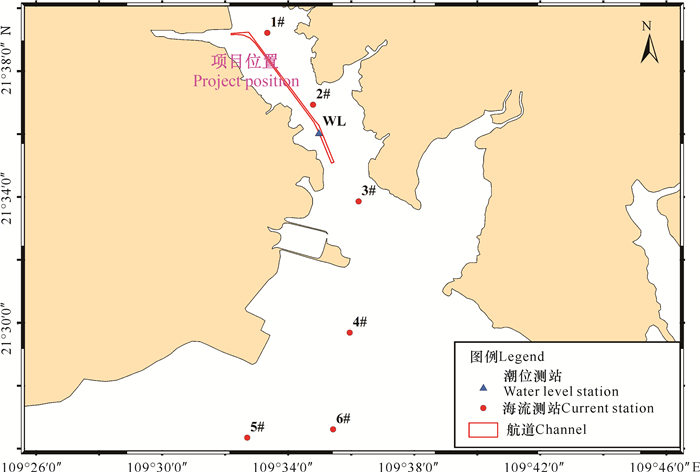
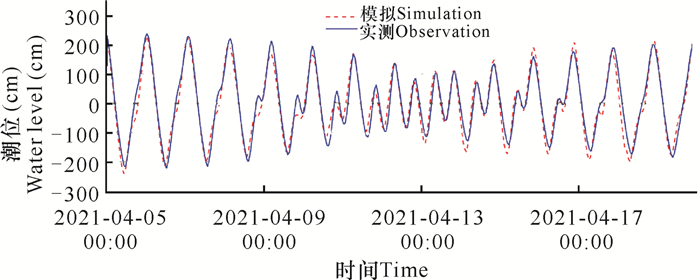
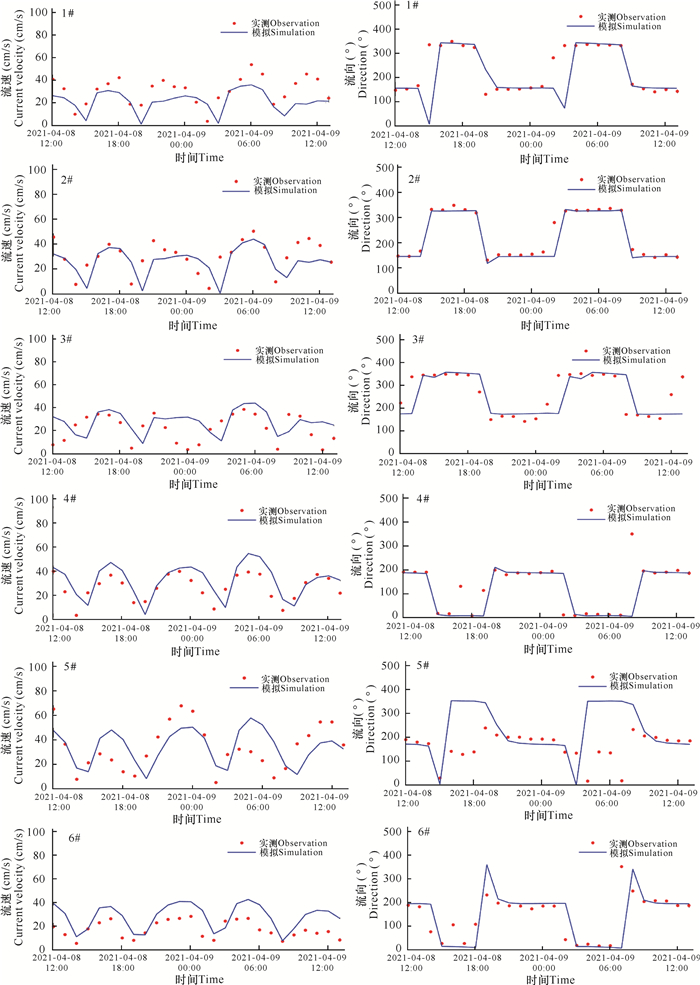
1.3 模型验证为验证模型的准确性,利用水动力模型模拟工程海域的潮位和潮流状况。将模拟结果与1个临时潮位站(WL)、6个潮流观测站(1#-6#)测量结果进行对比。观测站位置见图 4,水位模拟对比曲线见图 5,潮流模拟对比曲线见图 6。
|
| 图 4 实测站位分布图 Fig. 4 Distribution of observation stations |
|
| 图 5 潮位模拟实测对比曲线(2021年4月5日0时—2021年4月20日23时) Fig. 5 Comparison curve between simulation and measured data (0:00, April 5 - 23:00, April 20, 2021) |
|
| 图 6 流速流向验证图(2021年4月12日、13日) Fig. 6 Validation of current velocity and direction (April 12 to April 13, 2021) |
对比验证结果表明:潮位、潮流模拟结果与实测潮位、潮流资料基本吻合,能够较好地反映项目周边海域水位和潮流状况。
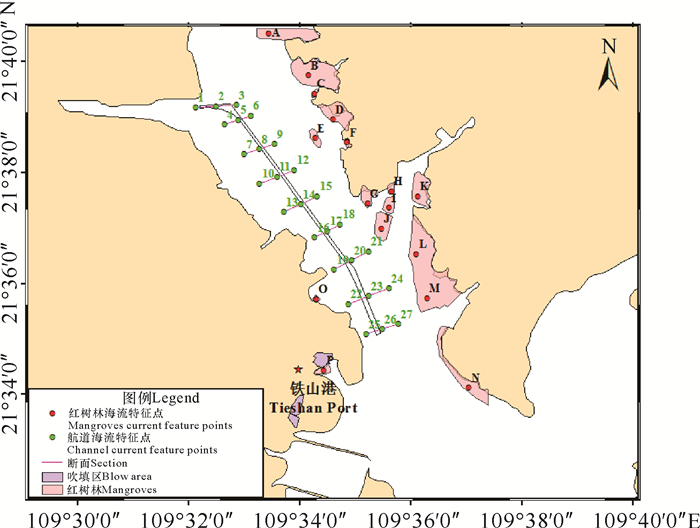
1.4 研究内容前述验证结果表明文章叙述的模型可以用于工程前后水动力改变情况的研究,为其提供数值模拟技术。为更直观地比较疏浚工程前后的变化情况,选取航道9个断面27个特征点的大潮期流速(图 7)进行对比分析。同时,为研究红树林区域水动力改变情况,选取铁山港东岸和西岸红树林内共16个特征点的流速进行对比分析(图 7)。
|
| 图 7 航道和红树林特征点分布 Fig. 7 Distribution of feature points in channel and mangrove |
2 结果与分析 2.1 疏浚工程前后潮流场分析
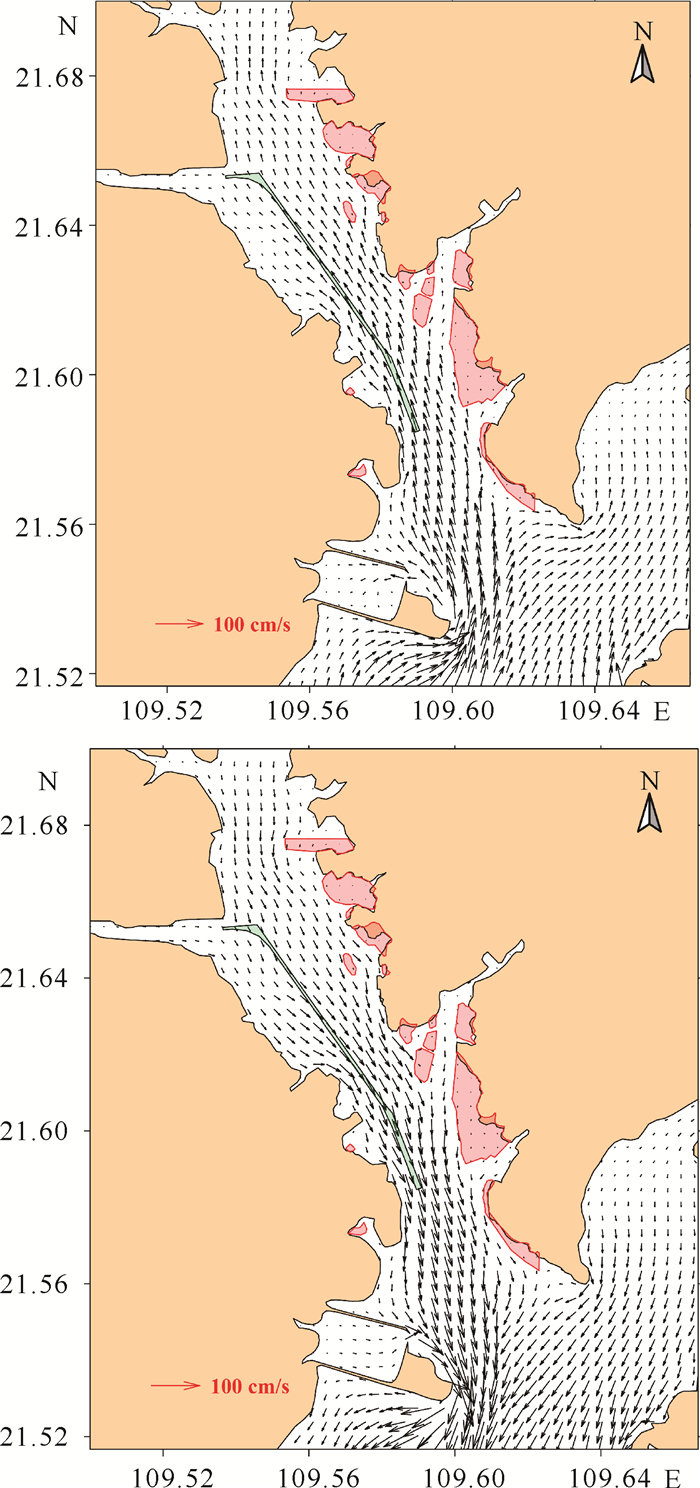
根据大潮期涨落急时刻流场图(图 8, 9)分析可知,由北部湾而来的潮流沿着西南向上溯。涨潮流以偏北向流为主,落潮流以偏南向流为主,涨潮流在英罗港西侧分成两股,一股向东进入英罗港,另一股折向西北上溯进入铁山港内湾;落潮时潮流则相反。铁山港深槽区域流速较大,岸边流速较小,岸边有浅滩出露。
|
| 图 8 大潮期涨急(上)和落急(下)时刻疏浚工程前航道附近海域流场图 Fig. 8 Flow field of sea area near the channel before dredging at the time of sharp rise (up) and sharp fall (down) |
|
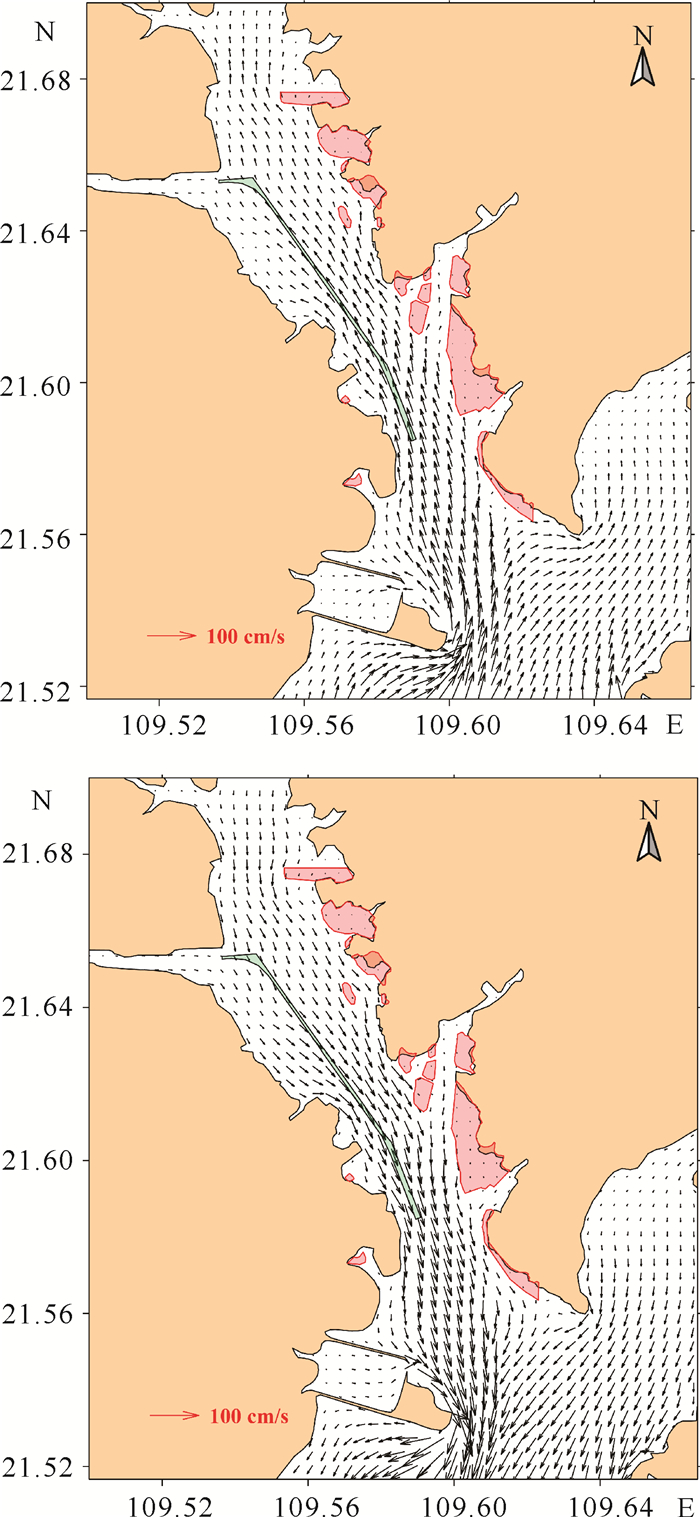
| 图 9 大潮期涨急(上)和落急(下)时刻疏浚工程后航道附近海域流场图 Fig. 9 Flow field of sea area near the channel after dredging at the time of sharp rise (up) and sharp fall (down) |
工程前,工程附近海域涨急时刻流速为9.2-50.4 cm/s,大致呈南高北低分布,最大流速出现在Ⅲ段南端附近;落急时刻,工程海域整体流速相比涨急时刻增大,同涨急类似,流速呈现南高北低分布,最大流速出现在工程南部海域,为68.2 cm/s(图 10)。
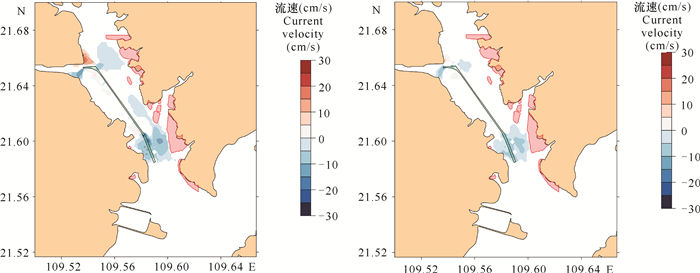
|
| 图 10 涨急(左)和落急(右)时刻疏浚工程前后航道附近海域流速变化 Fig. 10 Current velocity change of sea area near the channel after dredging at the time of sharp rise (left) and sharp fall (right) |
工程后,因疏浚造成水深增加,因此航道内流速呈现降低趋势。涨急时刻,航道内流速降低幅度为0-12 cm/s,航道南部周边区域降低值较大,超过10 cm/s,最大为11.7 cm/s。落急时刻,航道内流速降低幅度为0-5 cm/s,周边流速降低相对涨急时刻幅度减少,不足5 cm/s (图 10)。
航道大潮期流速变化如表 2所示。涨急时刻,各特征点工程后流速较工程前变化无规律,其中以4号特征点流速增加最多,最多增加6.3 cm/s;23号特征点流速降低最多,最多降低11.7 cm/s。落急时刻,4号特征点流速增加最多,最多增加3.7 cm/s;24号特征点流速降低最多,最多降低9.8 cm/s。
| 特征点编号 Feature point number |
涨急时刻Sharp rise | 落急时刻Sharp fall | |||||||
| 工程前流速(cm/s) Pre-engin-eering flowvelocity (cm/s) |
工程后流速(cm/s) Post engin-eering flowvelocity (cm/s) |
差值 Difference |
相对变化率(%) Relative rate of change (%) |
工程前流速(cm/s) Pre-engin-eering flowvelocity (cm/s) |
工程后流速(cm/s) Post engin-eering flow velocity (cm/s) |
差值 Difference |
相对变化率(%) Relative rate of change (%) |
||
| 1 | 11.3 | 2.6 | -8.7 | -77.0 | 10.8 | 7.4 | -3.4 | -31.5 | |
| 2 | 18.1 | 9.2 | -8.9 | -49.2 | 20.5 | 15.1 | -5.4 | -26.3 | |
| 3 | 13.5 | 12.1 | -1.4 | -10.4 | 23.7 | 17.9 | -5.8 | -24.5 | |
| 4 | 9.4 | 15.7 | 6.3 | 67.0 | 14.8 | 18.5 | 3.7 | 25.0 | |
| 5 | 9.2 | 14.8 | 5.6 | 60.9 | 16.6 | 18.2 | 1.6 | 9.6 | |
| 6 | 17.3 | 14.6 | -2.7 | -15.6 | 23.0 | 20.8 | -2.2 | -9.6 | |
| 7 | 9.8 | 11.9 | 2.1 | 21.4 | 14.2 | 15.6 | 1.4 | 9.9 | |
| 8 | 13.8 | 15.1 | 1.3 | 9.4 | 22.9 | 23.3 | 0.4 | 1.7 | |
| 9 | 17.4 | 17.2 | -0.2 | -1.1 | 26.4 | 26.1 | -0.3 | -1.1 | |
| 10 | 19.9 | 20.0 | 0.1 | 0.5 | 18.5 | 18.3 | -0.2 | -1.1 | |
| 11 | 25.0 | 24.1 | -0.9 | -3.6 | 32.2 | 32.3 | 0.1 | 0.3 | |
| 12 | 29.1 | 27.9 | -1.2 | -4.1 | 42.6 | 41.2 | -1.4 | -3.3 | |
| 13 | 20.9 | 20.5 | -0.4 | -1.9 | 26.8 | 27.9 | 1.1 | 4.1 | |
| 14 | 26.8 | 27.1 | 0.3 | 1.1 | 38.3 | 37.4 | -0.9 | -2.3 | |
| 15 | 31.4 | 30.3 | -1.1 | -3.5 | 46.9 | 44.9 | -2.0 | -4.3 | |
| 16 | 33.5 | 33.0 | -0.5 | -1.5 | 43.9 | 43.6 | -0.3 | -0.7 | |
| 17 | 34.3 | 35.9 | 1.6 | 4.7 | 47.3 | 46.7 | -0.6 | -1.3 | |
| 18 | 36.0 | 34.6 | -1.4 | -3.9 | 47.7 | 45.5 | -2.2 | -4.6 | |
| 19 | 30.0 | 30.1 | 0.1 | 0.3 | 46.0 | 47.6 | 1.6 | 3.5 | |
| 20 | 36.4 | 41.3 | 4.9 | 13.5 | 55.6 | 53.5 | -2.1 | -3.8 | |
| 21 | 35.5 | 32.5 | -3.0 | -8.5 | 44.4 | 42.0 | -2.4 | -5.4 | |
| 22 | 36.2 | 29.5 | -6.7 | -18.5 | 54.0 | 46.1 | -7.9 | -14.6 | |
| 23 | 48.7 | 37.0 | -11.7 | -24.0 | 68.2 | 59.0 | -9.2 | -13.5 | |
| 24 | 48.3 | 38.4 | -9.9 | -20.5 | 66.8 | 57.0 | -9.8 | -14.7 | |
| 25 | 39.2 | 38.0 | -1.2 | -3.1 | 53.7 | 50.4 | -3.3 | -6.1 | |
| 26 | 50.4 | 41.3 | -9.1 | -18.1 | 64.5 | 59.1 | -5.4 | -8.4 | |
| 27 | 41.4 | 35.8 | -5.6 | -13.5 | 54.0 | 50.3 | -3.7 | -6.9 | |
2.2 疏浚工程对红树林区域的影响
红树林区域大潮期流速变化如表 3所示。涨急时刻,各特征点工程后流速较工程前大部分呈现降低现象,其中以H号特征点流速降低最多,最多降低4.3 cm/s;N号特征点流速增加最多,最多增加值为0.7 cm/s。落急时刻,L号特征点流速增加最多,最多增加0.1 cm/s;M号特征点流速降低最多,最多降低0.7 cm/s。工程完成后,因疏浚造成海域水深增加,进而影响红树林区域的流速情况,致使区域流速较工程前降低,对红树林区域起到间接保护作用。
| 特征点编号 Feature point number |
涨急时刻Sharp rise | 落急时刻Sharp fall | |||||||
| 工程前流速(cm/s) Pre-engin-eering flowvelocity (cm/s) |
工程后流速(cm/s) Post engin-eering flowvelocity (cm/s) |
差值 Difference |
相对变化率(%) Relative rate of change(%) |
工程前流速(cm/s) Pre-engin-eering flowvelocity (cm/s) |
工程后流速(cm/s) Post engin-eering flowvelocity (cm/s) |
差值 Difference |
相对变化率(%) Relative rate of change(%) |
||
| A | 8.1 | 6.1 | -2.0 | -24.7 | 8.4 | 8.1 | -0.3 | -3.6 | |
| B | 2.3 | 1.8 | -0.5 | -21.7 | 2.5 | 2.3 | -0.2 | -8.0 | |
| C | 3.1 | 2.8 | -0.3 | -9.7 | 3.3 | 3.1 | -0.2 | -6.1 | |
| D | 6.1 | 2.0 | -4.1 | -67.2 | 6.4 | 6.1 | -0.3 | -4.7 | |
| E | 5.4 | 5.1 | -0.3 | -5.6 | 5.7 | 5.4 | -0.3 | -5.3 | |
| F | 2.3 | 1.0 | -1.3 | -56.5 | 2.4 | 2.3 | -0.1 | -4.2 | |
| G | 6.3 | 2.1 | -4.2 | -66.7 | 6.8 | 6.3 | -0.5 | -7.4 | |
| H | 6.2 | 1.9 | -4.3 | -69.4 | 6.7 | 6.2 | -0.5 | -7.5 | |
| I | 4.5 | 2.5 | -2.0 | -44.4 | 5.0 | 4.5 | -0.5 | -10.0 | |
| J | 4.0 | 3.5 | -0.5 | -12.5 | 4.4 | 4.0 | -0.4 | -9.1 | |
| K | 0.9 | 1.1 | 0.2 | 22.2 | 0.9 | 0.9 | 0.0 | 0.0 | |
| L | 1.7 | 1.7 | 0.0 | 0.0 | 1.6 | 1.7 | 0.1 | 6.2 | |
| M | 4.7 | 2.7 | -2.0 | -42.6 | 5.4 | 4.7 | -0.7 | -13.0 | |
| N | 2.2 | 2.9 | 0.7 | 31.8 | 2.3 | 2.2 | -0.1 | -4.3 | |
| O | 2.5 | 0.4 | -2.1 | -84.0 | 2.6 | 2.5 | -0.1 | -3.8 | |
| P | 0.6 | 0.5 | -0.1 | -16.7 | 0.6 | 0.6 | 0.0 | 0.0 | |
3 结论
因铁山港区Ⅲ航道疏浚工程的开展,该区域水动力环境发生改变。数值模拟结果显示, 涨急和落急时刻,各特征点工程后流速较工程前变化无规律;北部浅水区域因水深增加,造成流速增大;而南部深水区域,出现流速降低的现象,这主要和截面过流通量有关。
对红树林区域而言,涨急和落急时刻,各特征点工程后流速较工程前大部分呈现降低现象,其中以H号特征点流速降低最多,最多不超过5.0 cm/s;个别点出现流速增大的现象,但是增加量不足1 cm/s。由此可知,水动力的改变对红树林产生的影响较小。
跟前人研究结果[17, 18]相比,本研究在数值模型中,考虑光滩和红树林曼宁系数的差别,使模拟结果和实测结果更加接近,但是因缺乏红树林区域实测流速资料,因此模型的效果无法定量评价。同时,本研究在航道附近设置多条断面,分别在航道左侧、中间和右侧设置特征点,研究航道疏浚对航道内部及附近流场的改变,对比结果更加全面,可以明显看出因航道疏浚造成的水深增加,进而影响流速分布的情况。
| [1] |
辛文杰. 北海铁山港航道工程潮流数值计算分析[R]. 南京: 南京水利科学研究院, 1994.
|
| [2] |
陈波, 邱绍芳, 葛文标, 等. 广西沿岸主要海湾潮流的数值计算[J]. 广西科学, 2001, 8(4): 295-300. DOI:10.3969/j.issn.1005-9164.2001.04.015 |
| [3] |
施华斌, 牛小静, 余锡平. 北部湾及广西近海潮流数值模拟[J]. 清华大学学报(自然科学版), 2012, 52(6): 791-797. |
| [4] |
王丽娜, 潘伟然, 骆智斌, 等. 基于随机游动模型的铁山港水交换的数值模拟[J]. 厦门大学学报(自然科学版), 2014, 53(6): 840-847. |
| [5] |
李小维, 裴木凤. 铁山港湾港口总体规划用海对海水动力环境的影响预测[J]. 广西科学, 2015, 22(3): 274-280. |
| [6] |
YANG W K, YIN B S, FENG X R, et al. The effect of nonlinear factors on tide-surge interaction: A case study of Typhoon Rammasun in Tieshan Bay, China[J]. Estuarine, Coastal and Shelf Science, 2019, 219(5): 420-428. |
| [7] |
谢洁. 广西铁山港区潮流泥沙数值模拟[J]. 水运工程, 2011, 4(3): 1-9. |
| [8] |
刘文龙, 毛晨浩, 陈维, 等. 安海湾疏浚工程潮流响应特征研究[J]. 浙江海洋大学学报(自然科学版), 2021, 40(5): 439-448. DOI:10.3969/j.issn.1008-830X.2021.05.009 |
| [9] |
唐崇熙. 基于MIKE 21的白洋淀水动力与水质数值模拟研究[D]. 天津: 天津工业大学, 2021.
|
| [10] |
黄学智. 基于FVCOM的黄渤海潮汐潮流的数值模拟[D]. 大连: 大连海洋大学, 2016.
|
| [11] |
薛云红, 刘文爱. 铁山港红树林高岭土沉积区虫害及互花米草调查与分析[J]. 广西科学院学报, 2021, 37(3): 314-323. |
| [12] |
潘良浩, 史小芳, 范航清, 等. 广西铁山港围填海导致的高岭土快速沉积致红树林死亡原因分析[J]. 广西科学院学报, 2021, 37(3): 270-278. |
| [13] |
高霆炜, 杨明柳, 宋超. 海岸工程对北海铁山港红树林大型底栖动物群落的影响[J]. 广西科学院学报, 2021, 37(3): 299-306. |
| [14] |
王阳, 杨红, 张午. 基于MIKE21的江苏如东海上风电场泥沙冲淤数值模拟[J]. 海洋湖沼通报, 2021, 43(2): 48-57. |
| [15] |
PAWLOWICZ R, BEARDSLEY B, LENTZ S, 等. 用MATLAB的T_Tide程序进行包含误差估计的经典潮汐调和分析[J]. 地壳构造与地壳应力, 2012(2): 17-25. |
| [16] |
倪海祥, 张乔民, 赵焕庭. 海南东寨港红树林港湾潮汐动力研究[J]. 热带海洋, 1996(4): 17-25. |
| [17] |
张卓, 叶荣辉, 卜春春, 等. 北海铁山港建港方案对铁山湾潮流泥沙的影响研究[J]. 水道港口, 2009, 30(6): 402-407. |
| [18] |
官志鑫. 铁山湾海域潮流及风浪数值模拟研究[D]. 长沙: 长沙理工大学, 2012.
|



