The Moment Stability and Stabilization of Hybrid Stochastic Retarded Systems under Asynchronous Markovian Switching
0 Introduction Switched systems are a class of hybrid systems which are widely applied in many fields such as failure-prone manufacturing, traffic management, power systems, and networked control systems.Stability properties and control synthesis are the crucial and fundamental problems of these successful applications, which have been extensively studied (see, for instance and the references therein[1-5]).It has been shown that mode-dependent controller is more general, flexible and less conservative in solving control synthesis problems.Unfortunately, most of the work done on the mode-dependent controller is built upon the assumption that the switching signal of controller and the system modes are strictly synchronized.The so-called "asynchronous switching" which takes into account the detected delay of switching signal when implementing the controller may be reasonable in reality[6-7].However, asynchronous switching may lead to instability or performance degradation of the switched system due to the mismatched controller act on each subsystem.Therefore, asynchronous switching control is more realistic and challenging.Some salient results have been done on switched systems under asynchronous switching control, such as [6-12].The stabilization problem of switched linear systems with detected delay of switching signal was studied in [8].By using a novel Lyapunov-like function approach, the authors of [6] solved the stability and l2-gain problems for discrete-time switched systems with average dwell time and asynchronous switching.Some further result on asynchronous switching control for continuous-time and discrete-time switched systems were obtained in [10].Based on a new integral inequality and the piecewise Lyapunov-Krasovskii functional technique, the stabilization problem for a class of switched linear neutral systems under asynchronous switching was addressed in [12].
It should be pointed out that the above-mentioned results are only suitable for deterministic systems.As we all know, in real-world evolutionary processes, noise is unavoidable.The presence of noise can degrade the performance of the corresponding deterministic dynamics and even may drastically alter the system dynamics behaviors[13].Consequently, stochastic modeling has played an important role in areas of automatic control.Recent years, hybrid stochastic systems which driven by continuous-time Markov chains and Wiener process have been studied by many works, see [13-22].However, there is few work which has been done on hybrid stochastic systems with asynchronous switching control.For dwell-time-based asynchronous switching control, there is a general requirement (R):The detected delay of switching signal is less than the corresponding switching interval, see [23-25].However, this requirement seems to be difficult to meet for randomly switched systems due to the switching signal is a stochastic process.For example, in Markovian switching control, it is well known that almost every sample path of Markov chain is a right-continuous step function, i.e., for every sample path, the switching intervals is almost sure greater than zeros, but it is not easily to obtain the lower bound of the switching interval for all sample paths.Although the asynchronous Markovian switching issues have been studied[26-28], there is further room for investigation.For example, in [26-27], the authors only investigated the stability and stabilization of discrete-time Markovian jump systems via a time-delayed controller.Under the assumption R, Razumikhin-type stability criteria for hybrid stochastic retarded systems were established in [28], but the stability conditions depend on a sequence of stopping time caused by Markov chain, and thus resulting in inconvenient application and verification.
This paper revisits asynchronous Markovian switching control problem of hybrid stochastic retarded systems through considering the relationship among the sizes of detected delay of switching signal and the transition probabilities of Markov chain.In contrast to Halanay's inequality or Razumikhin-type analysis technique, an integral-inequality-estimation technique is proposed to establish pth moment exponential stability criteria irrespective of the sizes of the state delay for hybrid stochastic retarded systems with an asynchronous Markovian switching controller.For its application, the obtained results are applied to a class of stochastic delayed systems with asynchronous Markovian switching that include linear stochastic systems, recurrent neural networks.Moreover, the stabilizing mode-dependent controller is designed by solving a set of linear matrix inequalities (LMIs).Compared with the case of synchronous switching results[16-18], our results do not impose any restriction on the derivative of state delay.
1 System description and preliminaries Notation For a real symmetric matrix A, the notation A>(< , ≤, ≥)0 means that the matrix A is positive (negative, semi-negative, semi-positive) definite, and λmax(A), λmin(A), respectively, denote the largest and least eigenvalue of A. The symmetric elements of a symmetric matrix are denoted by *.‖·‖ denotes the Euclidean vector norm.For τ>0, let C([-τ, 0]; Rn) denote the space of continuous functions ϕ from [-τ, 0] to Rn with norm ‖ϕ‖τ=sup-τ≤s≤0‖ϕ(t+s)‖.For a given function ϕ(t)∈C([-τ, b]; Rn) with b>0 and t∈[0, b], the associated function ϕt∈C([-τ, 0]; Rn) is defined as ϕt (s)=ϕ(t+s), s∈[-τ, 0].C2, 1(Rn× R+; R+)denotes the family of all nonnegative functions V(x, t) on Rn× R+ that are twice continuously differentiable in x and once in t.Given a complete probability space (Ω, $\mathscr{F}$, P) with a natural filtration {$\mathscr{F}$t}t≥0 satisfying the usual conditions, let w(t)=(w1(t), …, wm(t))T∈ Rm be an m-dimensional Wiener process defined on the probability space.
Consider the following time-delay hybrid stochastic system
|
$
\left\{ \begin{array}{l}
{\rm{d}}x\left( t \right) = \left[ {{f_{\sigma \left( t \right)}}\left( {x\left( t \right),x\left( {t - \tau \left( t \right)} \right),t} \right) + } \right.\\
\;\;\;\;\;\;\left. {{h_{\sigma \left( t \right)}}\left( {x\left( t \right),t} \right){u_{\sigma \left( t \right)}}\left( {x\left( t \right)} \right)} \right]{\rm{d}}t + \\
\;\;\;\;\;\;{g_{\sigma \left( t \right)}}\left( {x\left( t \right),x\left( {t - \tau \left( t \right)} \right),t} \right){\rm{d}}w\left( t \right),t > {t_0},\\
{x_{{t_0}}}\left( s \right) = \varphi \left( s \right), - \bar \tau \le s \le 0,\sigma \left( {{t_0}} \right) = {\sigma _0},
\end{array} \right.
$
|
(1) |
where x(t)∈ Rn is the state variable.{σ(t), t≥t0} is a right-continuous Markov process defined on the probability space which takes values in the finite set $\mathscr{M}$ ={1, 2, …, N} with generator Π=(πij), i, j∈ $\mathscr{M}$, given by
|
$
\begin{array}{l}
{\rm{P}}\left\{ {\sigma \left( {t + \Delta t} \right) = j\left| {\sigma \left( t \right) = i} \right.} \right\} = \\
\left\{ \begin{array}{l}
{\pi _{ij}}\Delta t + o\left( {\Delta t} \right),i \ne j,\\
1 + {\pi _{ii}}\Delta t + o\left( {\Delta t} \right),i = j,
\end{array} \right.
\end{array}
$
|
where Δt>0, $\mathop {\lim }\limits_{\Delta t \to 0} \frac{{o\left( {\Delta t} \right)}}{{\left( {\Delta t} \right)}} = 0$, and πij≥0 for i≠j, πii≤0 with $\sum\nolimits_{j = 1, j \ne i}^N {{\pi _{ij}} =-{\pi _{ii}}} $.τ(t) are state delay satisfies 0≤τ(t)≤τ.For each i∈$\mathscr{M}$, fi: Rn× Rn× R+→ Rn, gi: Rn× Rn× R+→ Rn×m, hi: Rn× R+→ Rn×n0, and ui: Rn→ Rn0×n is mode-dependent control input which is used to achieve system stability or certain performances.
It is noted that in the controlled system (1), the control input is coincident with the switching rule.However, just as [6-7] point out that this requirement is hard to be satisfied in the physical systems, the control input may exist a time delay which is induced by the identification of the system modes or the implementation of the matched controller.That is, the control input uσ(t)(x(t)) should be modified by uσ(t-δ)(x(t)), where δ>0 and σ(t-δ)=σ0 if t≤δ.Hence, the resulting closed-loop system is given by
|
$
\left\{ \begin{array}{l}
{\rm{d}}x\left( t \right) = \left[ {{f_{\sigma \left( t \right)}}\left( {x\left( t \right),x\left( {t - \tau \left( t \right)} \right),t} \right)} \right. + \\
\;\;\;\;\;\;\left. {{h_{\sigma \left( t \right)}}\left( {x\left( t \right),t} \right){u_{\sigma \left( {t - \delta } \right)}}\left( {x\left( t \right)} \right)} \right]{\rm{d}}t + \\
\;\;\;\;\;\;{g_{\sigma \left( t \right)}}\left( {x\left( t \right),x\left( {t - \tau \left( t \right)} \right),t} \right){\rm{d}}w\left( t \right),t > {t_0},\\
{x_{{t_0}}}\left( s \right) = \varphi \left( s \right), - \bar \tau \le s \le 0,\sigma \left( {{t_0}} \right) = {\sigma _0},
\end{array} \right.
$
|
(2) |
Obviously, because of the existence of the mismatched control input, it may degrade the performances and even cause instability if applying the matched control input and the switching signal designed for system (1) to system (2).Therefore, this paper attempts to establish general stability criteria for the hybrid stochastic system under asynchronous Markovian switching, and quantitatively analyze the effect of the detected delay of switching signal on the stability performance.For this purpose, we always assume that for each i, j∈$\mathscr{M}$, ${{\tilde f}_{ij}}$(0, 0, t)≡0, gi(0, 0, t)≡0, for all t≥t0, and both ${{\tilde f}_{ij}}$(x, y, t) and gi(x, y, t) satisfy the local Lipschitz condition and linear growth condition, where ${{\tilde f}_{ij}}$(x, y, t)=fi(x, y, t)+hi(x, t)uj(x).Hence, it follows from Theorem 8.3 of [13] that system (2) has a unique global solution, and x(t; t0, 0)=0 is the trivial solution.
For each i∈$\mathscr{M}$, if Vi∈C2, 1(Rn× R+; R+), define an operator associated with (2) by
|
$
\begin{array}{l}
\mathscr{L}V\left( {{x_t},t,i,j} \right) = {G_i}\left( {x\left( t \right),x\left( {t - \tau \left( t \right)} \right),t} \right) + \\
\Delta {G_{i,j}}\left( {x\left( t \right),t} \right),
\end{array}
$
|
where
|
$
\begin{array}{l}
{G_i}\left( {x,y,t} \right) = \frac{{\partial {V_i}\left( {x,t} \right)}}{{\partial t}} + \frac{{\partial {V_i}\left( {x,t} \right)}}{{\partial x}} \cdot \\
\left[ {{f_i}\left( {x,y,t} \right) + {h_i}\left( {x,t} \right){u_i}\left( x \right)} \right] + \\
\frac{1}{2}{\rm{trace}}\left[ {g_i^{\rm{T}}\left( {x,y,t} \right)\frac{{{\partial ^2}{V_i}\left( {x,t} \right)}}{{\partial {x^2}}}{g_i}\left( {x,y,t} \right)} \right] + \\
\sum\limits_{j = 1}^N {{\pi _{ij}}{V_j}\left( {x,t} \right)} ,
\end{array}
$
|
|
$
\Delta {G_{i,j}}\left( {x,t} \right) = \frac{{\partial {V_i}\left( {x,t} \right)}}{{\partial x}}{h_i}\left( {x,t} \right)\left( {{u_j}\left( x \right) - {u_i}\left( x \right)} \right).
$
|
Then the generalized Itô formula[13] can be given as follows
|
$
\begin{array}{l}
{\rm{E}}{V_{\sigma \left( {{t_2}} \right)}}\left( {x\left( {{t_2}} \right),{t_2}} \right) = {\rm{E}}{V_{\sigma \left( {{t_1}} \right)}}\left( {x\left( {{t_1}} \right),{t_1}} \right) + \\
{\rm{E}}\int_{{t_1}}^{{t_2}} {\mathscr{L}V\left( {{x_s},s,\sigma \left( s \right),\sigma \left( {s - \delta } \right)} \right){\rm{d}}s} ,{t_2} \ge {t_1} \ge {t_0}.
\end{array}
$
|
(3) |
To make this paper more readable, we give the definition of pth moment exponential stability.
Definition 1 The zero solution of system (2) is pth-moment exponentially stable, if there exist two positive scalars M and γ such that
|
$
{\rm{E}}{\left\| {x\left( t \right)} \right\|^p} \le M{\rm{E}}{\left\| \varphi \right\|^{\frac{p}{\tau }}}{{\rm{e}}^{ - \gamma \left( {t - {t_0}} \right)}},t \ge {t_0}.
$
|
2 Stability analysis Theorem 1 Consider hybrid stochastic system (2), if there exist nonnegative functions Vi∈C2, 1(Rn× R+; R+), positive constants c, c, ξ1, ξ2, ci, j, j≠i, such that for any x, y∈ Rn, i, j∈$\mathscr{M}$, the following conditions hold:
|
$
\underline c {\left\| x \right\|^p} \le {V_i}\left( {x,t} \right) \le \bar c{\left\| x \right\|^p},
$
|
(4) |
|
$
{G_i}\left( {x,y,t} \right) \le - {\xi _1}{\left\| x \right\|^p} + {\xi _2}{\left\| y \right\|^p},
$
|
(5) |
|
$
\Delta {G_{i,j}}\left( {x,t} \right) \le {c_{i,j}}{\left\| x \right\|^p},j \ne i,
$
|
(6) |
|
$
\bar c{\xi _2} + \underline c \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{c_{i,j}}{{\rm{P}}_{ji}}\left( \delta \right)} } < \underline c {\xi _1},
$
|
(7) |
where eΠδ=(Pij(δ))N×N, then system (2) is pth-moment exponentially stable.
Proof Set W(t)=eγ(t-t0)Vσ(t)(x(t), t), where γ= $\frac{{{\xi _1}\sum\nolimits_{j = 1}^N {\sum\nolimits_{j = 1, j \ne i}^N {{c_{i, j}}{{\rm{P}}_{ji}}\left( \delta \right)} } }}{c}$.Applying the generalized Itô formula to W(t) and utilizing conditions (5) and (6), we have
|
$
\begin{array}{l}
{\rm{E}}W\left( t \right) = {\rm{E}}W\left( {{t_0}} \right) + {\rm{E}}\int_{{t_0}}^t {{{\rm{e}}^{\gamma \left( {s - {t_0}} \right)}}\left[ {\gamma {V_{\sigma \left( s \right)}}\left( {x\left( s \right),s} \right) + } \right.} \\
\left. {\mathscr{L}V\left( {{x_s},s,\sigma \left( s \right),\sigma \left( {s - \delta } \right)} \right)} \right]{\rm{d}}s \le {\rm{E}}W\left( {{t_0}} \right) + \\
{\rm{E}}\int_{{t_0}}^t {{e^{\gamma \left( {s - {t_0}} \right)}}\left[ {\left( {\gamma \bar c - {\xi _1} + {c_{\sigma \left( s \right),\sigma \left( {s - \delta } \right)}}} \right){{\left\| {x\left( s \right)} \right\|}^p} + } \right.} \\
\left. {{\xi _2}{{\left\| {x\left( {s - \tau \left( s \right)} \right)} \right\|}^p}} \right]{\rm{d}}s.
\end{array}
$
|
Let ci, i=0, i∈$\mathscr{M}$, then for any t≥t0,
|
$
\begin{array}{l}
{c_{\sigma \left( t \right),\sigma \left( {t - \delta } \right)}} = \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{c_{i,j}}{I_{\left\{ {\sigma \left( t \right) = i} \right\}}}{I_{\left\{ {\sigma \left( {t - \delta } \right) = j} \right\}}}} } = \\
\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{c_{i,j}}{\rm{E}}\left\{ {{I_{\left\{ {\sigma \left( t \right) = i} \right\}}}{I_{\left\{ {\sigma \left( {t - \delta } \right) = j} \right\}}}\left| {{\mathscr{F}_{t - \delta }}} \right.} \right\}} } = \\
\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{c_{i,j}}{I_{\left\{ {\sigma \left( {t - \delta } \right) = j} \right\}}}{\rm{E}}\left\{ {{I_{\left\{ {\sigma \left( t \right) = i} \right\}}}\left| {{\mathscr{F}_{t - \delta }}} \right.} \right\}} } = \\
\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{c_{i,j}}{I_{\left\{ {\sigma \left( {t - \delta } \right) = j} \right\}}}{\rm{P}}\left\{ {\sigma \left( t \right) = i\left| {\sigma \left( {t - \delta } \right) = j} \right.} \right\}} } = \\
\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{c_{i,j}}{I_{\left\{ {\sigma \left( {t - \delta } \right) = j} \right\}}}{{\rm{P}}_{ji}}\left( \delta \right)} } \le \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{c_{i,j}}{{\rm{P}}_{ji}}\left( \delta \right)} } .
\end{array}
$
|
Based on this fact, we have
|
$
\begin{array}{l}
{\rm{E}}W\left( t \right) \approx {\rm{E}}W\left( {{t_0}} \right) + {\xi _2}\int_{{t_0}}^t {{{\rm{e}}^{\gamma \left( {s - {t_0}} \right)}}{\rm{E}}\left\| {x\left( {s - } \right.} \right.} \\
{\left. {\left. {\tau \left( s \right)} \right)} \right\|^p}{\rm{d}}s.
\end{array}
$
|
Applying (4) again, the above inequality can be transferred to
|
$
\begin{array}{l}
{{\rm{e}}^{\gamma \left( {t - {t_0}} \right)}}{\rm{E}}{\left\| {x\left( t \right)} \right\|^p} \le \frac{{\bar c}}{{\underline c }}{\rm{E}}{\left\| \varphi \right\|^{\frac{p}{\tau }}} + \\
\frac{{{\xi _2}}}{{\underline c }}\int_{{t_0}}^t {{{\rm{e}}^{\gamma \left( {s - {t_0}} \right)}}{\rm{E}}{{\left\| {x\left( {s - \tau \left( s \right)} \right)} \right\|}^p}{\rm{d}}s} .
\end{array}
$
|
(8) |
Define a strictly monotonically increasing function $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho }\left( t \right)=\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c}\bar{c}t+\bar{c}{{\xi }_{2}}{{\rm{e}}^{t\bar{\tau }}}+\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c}\sum\nolimits_{j=1}^{N}{\sum\nolimits_{j=1, j\ne i}^{N}{{{c}_{i, j}}{{\rm{P}}_{ji}}\left( \delta \right)}}-\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c}{{\xi }_{1}}$, then it follows from (7) that ρ (0) < 0 and ρ (γ)=c ξ2eγτ>0.According to the intermediate value theorem, there exist a constant η∈(0, γ) such that ρ(η)=0, whence $\frac{{{\xi }_{2}}{{\rm{e}}^{\eta \bar{\tau }}}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c}\left( \gamma-\eta \right)}=1$.In the sequel, we will show that for any $\epsilon $>1,
|
$
\begin{align}
&{\rm{E}}{{\left\| x\left( t \right) \right\|}^{p}}\le \frac{{\bar{c}}}{\underline{c}}{\rm{E}}{{\left\| \varphi \right\|}^{\frac{p}{\tau }}}{{\rm{e}}^{-\eta \left( t-{{t}_{0}} \right)}}< \\
&\epsilon M{{\rm{e}}^{-\eta \left( t-{{t}_{0}} \right)}},\forall t\ge {{t}_{0}}-\bar{\tau }, \\
\end{align}
$
|
(9) |
where $M=\frac{{\bar{c}}}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c}}}{\rm{E}}{{\left\| \varphi \right\|}^{\frac{p}{\tau }}}$.If (9) is not true, then by the continuity of E‖x(t)‖p on (t0, +∞), there exists t1>t0 such that E‖x(t1)‖p≥$\epsilon $ Me-η (t1-t0).Let t*=inf{t∈(t0, t1], E‖x(t)‖p≥ $\epsilon $ Me-η (t-t0)}, we have
|
$
\begin{align}
&{\rm{E}}{{\left\| x\left( {{t}^{*}} \right) \right\|}^{p}}=\epsilon M{{\rm{e}}^{-\eta \left( {{t}^{*}}-{{t}_{0}} \right)}},{\rm{E}}{{\left\| x\left( s \right) \right\|}^{p}}< \\
&\epsilon M{{\rm{e}}^{-\eta \left( t-{{t}_{0}} \right)}},{\rm{for}} \ {\rm{all}} \ s\in \left[ {{t}_{0}}-\bar{\tau },{{t}^{*}} \right). \\
\end{align}
$
|
Then inequality (8) has the estimation at t*
|
$
\begin{align}
&{{\rm{e}}^{\gamma \left( {{t}^{*}}-{{t}_{0}} \right)}}{\rm{E}}{{\left\| x\left( {{t}^{*}} \right) \right\|}^{p}}\le M+ \\
&\frac{{{\xi }_{2}}}{\underline{c}}\int_{{{t}_{0}}}^{{{t}^{*}}}{{{\rm{e}}^{\gamma \left( s-{{t}_{0}} \right)}}\epsilon M{{\rm{e}}^{-\eta \left( s-\tau \left( s \right)-{{t}_{0}} \right)}}{\rm{d}}s}\le M+ \\
&\frac{{{\xi }_{2}}}{\underline{c}}{{\rm{e}}^{\eta \bar{\tau }}}\epsilon M\int_{{{t}_{0}}}^{{{t}^{*}}}{{{\rm{e}}^{\left( \gamma -\eta \right)\left( s-{{t}_{0}} \right)}}{\rm{d}}s}<\epsilon M\left( 1-\frac{{{\xi }_{2}}{{\rm{e}}^{\eta \bar{\tau }}}}{\underline{c}\left( \gamma -\eta \right)} \right)+ \\
&\frac{{{\xi }_{2}}{{\rm{e}}^{\eta \bar{\tau }}}}{\underline{c}\left( \gamma -\eta \right)}\epsilon M{{\rm{e}}^{\left( \gamma -\eta \right)\left( {{t}^{*}}-{{t}_{0}} \right)}}={\rm{E}}{{\left\| x\left( {{t}^{*}} \right) \right\|}^{p}}{{\rm{e}}^{\gamma \left( {{t}^{*}}-{{t}_{0}} \right)}}, \\
\end{align}
$
|
which leads to a contradiction.Therefore, (9) holds.Letting $\epsilon $→1+ in (9), it follows that
|
$
{\rm{E}}{\left\| {x\left( t \right)} \right\|^p} \le \frac{{\bar c}}{{\underline c }}{\rm{E}}{\left\| \varphi \right\|^{\frac{p}{\tau }}}{{\rm{e}}^{ - \eta \left( {t - {t_0}} \right)}}.
$
|
Therefore, system (2) is pth-moment exponentially stable.
Remark 1 Theorem 1 reveals that if the synchronous switched controlled system (1) is pth-moment exponentially stable (i.e.the conditions (4), (5) and (7) with δ=0 hold), then there exists a small enough δ such that the asynchronous switched controlled system (2) is also pth-moment exponentially stable.Actually, it follows from (7) that the admissible time delay of mismatched switching can be easily calculated for the synchronous switched controlled systems with the pre-designed controller and the generator of Markov chain.On the other hand, it is interesting to compare our result with existing results for the case of synchronous switched systems.Compared with results [16-18], the conditions of Theorem 1 is not only irrespective of the sizes of the state delay but also does not impose any restriction on the derivative of the delay.Different from the Razumikhin-type results[13, 19, 22], Theorem 1 is established by utilizing proofs by contradiction to estimate an integral inequality, and thus leading to simpler stability conditions.
For the constant delay case, condition (7) of Theorem 1 can be relaxed.That is, if we set τ(t)≡τ, then we have the following result.
Corollary 1 Consider hybrid stochastic system (2), if there exist nonnegative functions Vi∈C2, 1(Rn× R+; R+), positive constants c, c, ξ1, ξ2, ci, j, j≠ i, such that for any x, y∈ Rn, i, j∈$\mathscr{M}$, the following conditions hold:
|
$
\underline c {\left\| x \right\|^p} \le {V_i}\left( {x,t} \right) \le \bar c{\left\| x \right\|^p},
$
|
(10) |
|
$
{G_i}\left( {x,y,t} \right) \le - {\xi _1}{\left\| x \right\|^p} + {\xi _2}{\left\| y \right\|^p},
$
|
(11) |
|
$
\Delta {G_{i,j}}\left( {x,t} \right) \le {c_{i,j}}{\left\| x \right\|^p},j \ne i,
$
|
(12) |
|
$
{\xi _2} + \sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{c_{i,j}}{{\rm{P}}_{ji}}\left( \delta \right)} } < {\xi _1},
$
|
(13) |
where eΠδ=(Pij(δ))N×N, then system (2) is pth-moment exponentially stable.
Proof Choose a Lyapunov function for system (2):W(t)=eγ(t-t0)Vσ(t)(x(t), t), where γ is a unique positive solution of $\bar{c}\bar{\gamma }+{{\xi }_{2}}{{\rm{e}}^{\bar{\gamma }\tau }}+\sum\nolimits_{j=1}^{N}{\sum\nolimits_{j=1, j\ne i}^{N}{{{c}_{i, j}}{{\rm{P}}_{ji}}\left( \delta \right)}}-{{\xi }_{1}}=0$.Applying the same technique used above, we have
|
$
\begin{array}{l}
{\rm{E}}\bar W\left( t \right) \le {\rm{E}}\bar W\left( {{t_0}} \right) + {\rm{E}}\int_{{t_0}}^t {{{\rm{e}}^{\bar \gamma \left( {s - {t_0}} \right)}}\left[ {\left( {\bar c\bar \gamma - {\xi _1} + } \right.} \right.} \\
\left. {\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{c_{i,j}}{{\rm{P}}_{ji}}\left( \delta \right)} } } \right){\left\| {x\left( s \right)} \right\|^p} + {\xi _2}\left\| {x\left( {t - } \right.} \right.\\
\left. {{{\left. {\left. \tau \right)} \right\|}^p}} \right]{\rm{d}}s \le {\rm{E}}\bar W\left( {{t_0}} \right) + \left( {\bar c\bar \gamma - {\xi _1} + } \right.\\
\left. {\sum\limits_{i = 1}^N {\sum\limits_{j = 1,j \ne i}^N {{c_{i,j}}{{\rm{P}}_{ji}}\left( \delta \right)} } } \right){\rm{E}}\int_{{t_0}}^t {{{\rm{e}}^{\bar \gamma \left( {s - {t_0}} \right)}}{{\left\| {x\left( s \right)} \right\|}^p}{\rm{d}}s + } \\
{\xi _2}{{\rm{e}}^{\bar \gamma \tau }}{\rm{E}}\left[ {\int_{{t_0} - \tau }^{{t_0}} {{{\rm{e}}^{\bar \gamma \left( {s - {t_0}} \right)}}{{\left\| {x\left( s \right)} \right\|}^p}{\rm{d}}s + } } \right.\\
\left. {\int_{{t_0}}^{t - \tau } {{{\rm{e}}^{\bar \gamma \left( {s - {t_0}} \right)}}{{\left\| {x\left( s \right)} \right\|}^p}{\rm{d}}s} } \right] \le \left[ {\bar c + \left( {1 - } \right.} \right.\\
\left. {\left. {{e^{ - \bar \gamma \tau }}} \right){\xi _2}{{\rm{e}}^{\bar \gamma \tau }}/\bar \gamma } \right]{\rm{E}}\left\| \varphi \right\|_\tau ^p.
\end{array}
$
|
This implies that E‖x(t)‖p≤$\frac{\bar{c}+\left( 1-{{\rm{e}}^{\bar{\gamma }\tau }} \right){{\xi }_{2}}{{\rm{e}}^{\bar{\gamma }\tau }}/\bar{\gamma }}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c}}}\rm{E}\left\| \varphi \right\|_{\tau }^{p}{{\rm{e}}^{-\bar{\gamma }\left( t-{{t}_{0}} \right)}}$.The proof is complete.
3 Application Some theoretical results of asynchronous Markovian switching control for a nonlinear hybrid stochastic system are established in the previous section.We now apply these results to establish an LMI-based stability condition and solve the controller design problem for a class of nonlinear stochastic systems under asynchronous Markovian switching.The considered nonlinear stochastic systems include linear systems, recurrent neural networks, some chaotic systems and so forth, which is given by the following stochastic differential equations
|
$
\left\{ \begin{array}{l}
{\rm{d}}x\left( t \right) = \left[ {{C_{\sigma \left( t \right)}}x\left( t \right) + {A_{0,\sigma \left( t \right)}}{f_{\sigma \left( t \right)}}\left( {x\left( t \right),t} \right) + } \right.\\
\;\;\;\;\;\;\;{A_{1,\sigma \left( t \right)}}{f_{\sigma \left( t \right)}}\left( {x\left( {t - \tau } \right),t} \right) + \\
\;\;\;\;\;\;\;\left. {{B_{\sigma \left( t \right)}}u\left( t \right)} \right]{\rm{d}}t + {g_{\sigma \left( t \right)}}\left( {x\left( t \right),} \right.\\
\;\;\;\;\;\;\;\left. {x\left( {t - \tau } \right),t} \right){\rm{d}}w\left( t \right),t > {t_0},\\
{x_{{t_0}}}\left( s \right) = \varphi \left( s \right),s \in \left[ { - \tau ,0} \right],\sigma \left( {{t_0}} \right) = {\sigma _0},
\end{array} \right.
$
|
(14) |
where Ci, A0, i, A1, i∈ Rn×n, and Bi∈ Rn×n0 are known constant matrices.The control input is constructed by a mode-dependent state-feedback controller with delayed switching signal:
|
$
u\left( t \right) = {K_{\sigma \left( {t - \delta } \right)}}x\left( t \right),
$
|
(15) |
where Ki∈ Rn0×n and δ>0.
In the following, we will assume that the nonlinear functions fi (x, t)and gi(x, y, t), i∈ $\mathscr{M}$, satisfy the following assumptions.
(A1) For each i∈ $\mathscr{M}$, there exists a matrix Li with appropriate dimension such that
|
$
\left\| {{f_i}\left( {x,t} \right)} \right\| \le \left\| {{L_i}x} \right\|,\forall x \in {{\bf{R}}^n},\forall t \in {\bf{R}}.
$
|
(A2) For each i∈$\mathscr{M}$, there exist real matrices G1i≥0 and G2i≥0 such that
|
$
\begin{array}{l}
{\rm{trace}}\left[ {g_i^{\rm{T}}\left( {x,y,t} \right){g_i}\left( {x,y,t} \right)} \right] \le {x^{\rm{T}}}{G_{1i}}x + \\
{y^{\rm{T}}}{G_{2i}}y,\forall x,y \in {{\bf{R}}^n},\forall t \in {\bf{R}}.
\end{array}
$
|
3.1 Mean-square stability criterion Theorem 2 Consider the Markovian jump system (14) with (15) satisfying (A1) and (A2). For given Ki∈ Rn0×n and detected delay of switching signal δ, if there exist positive matrices Pi∈ Rn×n, and positive scalars βi, ξl, αli, and ci, j, i, j∈ $\mathscr{M}$, j≠i, l=1, 2, such that (13) and the following LMIs hold:
|
$
{P_i} \le {\beta _i}I,
$
|
(16) |
|
$
{\mathit{\Xi }_i} \buildrel \Delta \over = \left[ {\begin{array}{*{20}{c}}
{{\mathit{\Phi }_i}}&0&{{P_i}{A_{0,i}}}&{{P_i}{A_{1,i}}}\\
* &{{\mathit{\Psi }_i}}&0&0\\
*&* &{ - {\alpha _{1i}}I}&0\\
*&*&* &{ - {\alpha _{2i}}I}
\end{array}} \right] < 0,i \in \mathscr{M},
$
|
(17) |
|
$
\begin{array}{l}
{P_i}{B_i}\left( {{K_j} - {K_i}} \right) + {\left( {{K_j} - {K_i}} \right)^{\rm{T}}}B_i^{\rm{T}}{P_i} - {c_{i,j}}I \le 0,\\
i,j \in \mathscr{M},j \ne i,
\end{array}
$
|
(18) |
where
|
$
\begin{array}{l}
{\mathit{\Phi }_i} = {P_i}\left( {{C_i} + {B_i}{K_i}} \right) + {\left( {{C_i} + {B_i}{K_i}} \right)^{\rm{T}}}{P_i} + {\beta _i}{G_{1i}} + \\
{\alpha _{1i}}L_i^{\rm{T}}{L_i} + {\xi _1}I + \sum\limits_{j = 1}^N {{{\rm{ \mathsf{ π} }}_{ij}}{P_j}} ,
\end{array}
$
|
|
$
{\mathit{\Psi }_i} = - {\xi _2}I + {\beta _i}{G_{2i}} + {\alpha _{2i}}L_i^{\rm{T}}{L_i},
$
|
then system (14) with (15) is mean-square exponentially stable.
Proof Define a stochastic Lyapunov function candidate Vσ(t)(x(t))=xT(t)Pσ(t)x(t) for system (14).Firstly, we compute Gi(x, y, t) along the trajectories of system (15).
|
$
\begin{array}{l}
{G_i}\left( {x,y,t} \right) = {x^{\rm{T}}}\left( t \right)\left[ {{P_i}\left( {{C_i} + {B_i}{K_i}} \right) + \left( {{C_i} + } \right.} \right.\\
\left. {{{\left. {{B_i}{K_i}} \right)}^{\rm{T}}}{P_i} + \sum\limits_{j = 1}^N {{{\rm{ \mathsf{ π} }}_{ij}}{P_j}} } \right]x\left( t \right) + 2{x^{\rm{T}}}\left( t \right){P_i}{A_{0,i}}{f_i}\left( {x,t} \right) + \\
2{x^{\rm{T}}}\left( t \right){P_i}{A_{1,i}}f\left( {x\left( {t - \tau } \right),t} \right) + {\rm{trace}}\left[ {g_i^{\rm{T}}\left( {x\left( t \right),x\left( {t - } \right.} \right.} \right.\\
\left. {\left. {\left. \tau \right),t} \right){P_i}{g_i}\left( {x\left( t \right),x\left( {t - \tau } \right),t} \right)} \right].
\end{array}
$
|
(19) |
Using condition (16) and (A2), we have
|
$
\begin{array}{l}
{\rm{trace}}\left[ {g_i^{\rm{T}}\left( {x\left( t \right),x\left( {t - \tau } \right),t} \right){P_i}{g_i}\left( {x\left( t \right),x\left( {t - \tau } \right),} \right.} \right.\\
\left. {\left. t \right)} \right] \le {\beta _i}{x^{\rm{T}}}\left( t \right){G_{1i}}x\left( t \right) + {\beta _i}{x^{\rm{T}}}\left( {t - \tau } \right){G_{2i}}x\left( {t - \tau } \right).
\end{array}
$
|
(20) |
On the other hand, it can be deduced from (A1) that
|
$
\begin{array}{l}
0 \le \sum\limits_{l = 1}^2 {{\alpha _{li}}\left[ {{x^{\rm{T}}}\left( {t - {\tau _l}} \right)L_i^{\rm{T}}{L_i}\left( {t - {\tau _l}} \right) - f_i^{\rm{T}}\left( {x\left( {t - } \right.} \right.} \right.} \\
\left. {\left. {\left. {{\tau _l}} \right),t} \right){f_i}\left( {x\left( {t - {\tau _i}} \right),t} \right)} \right].
\end{array}
$
|
(21) |
where τ1=0 and τ2=τ.
Applying the inequalities (20)-(21) to (19) yields
|
$
\begin{array}{l}
{G_i}\left( {x,x\left( {t - \tau } \right),t} \right) \le \zeta _i^{\rm{T}}\left( t \right){\mathit{\Xi }_i}{\zeta _i}\left( t \right) - \\
{\xi _1}{\left\| {x\left( t \right)} \right\|^2} + {\xi _2}{\left\| {x\left( {t - \tau } \right)} \right\|^2}.
\end{array}
$
|
where ζi(t)=col(x(t), x(t-τ), fi(x(t), t), fi(x(t-τ), t)).Then, by (17), we obtain
|
$
{G_i}\left( {x,x\left( {t - \tau } \right),t} \right) \le - {\xi _1}{\left\| {x\left( t \right)} \right\|^2} + {\xi _2}{\left\| {x\left( {t - \tau } \right)} \right\|^2}.
$
|
Next, we calculate ΔGij(x(t), t).
|
$
\begin{array}{l}
\Delta {G_{ij}}\left( {x\left( t \right),t} \right) = {x^{\rm{T}}}\left( t \right)\left[ {{P_i}{B_i}\left( {{K_j} - {K_i}} \right) + \left( {{K_j} - } \right.} \right.\\
\left. {{{\left. {{K_i}} \right)}^{\rm{T}}}B_i^{\rm{T}}{P_i} - {c_{ij}}I} \right]x\left( t \right) + {c_{ij}}{\left\| {x\left( t \right)} \right\|^2}.
\end{array}
$
|
Inequality (18) implies that ΔGij(x(t), t)≤cij‖x(t)‖2.Therefore, by Theorem 1, we conclude that the zero solution of system (14) is mean-square exponentially stable.
3.2 Controller design Based on the mean-square stability criterion, this subsection will solve controller synthesis problem.For this purpose, assume ${{G}_{li}}=\bar{G}_{li}^{\rm{T}}{{{\bar{G}}}_{li}}$, i∈$\mathscr{M}$, l=1, 2, and then we introduce two lemmas.
Lemma 1 [29] For matrices $\mathscr{A}$∈ Rn×N, $\mathscr{B}$∈ RN×n, ${{{\mathit{\tilde{\Xi }}}}_{i}}$∈ RN×N, ${{{\mathit{\tilde{\Xi }}}}_{i}}=\mathit{\tilde{\Xi }}_{i}^{\rm{T}}$, X0, Xi, Hi∈ Rn×n, i=1, 2, …, p, if they satisfy the following inequalities for all i∈{1, …, p}:
|
$
\left[ {\begin{array}{*{20}{c}}
{{{\mathit{\tilde \Xi }}_i} + \mathscr{B}{X_0}\mathscr{A} + {{\left( {\mathscr{B}{X_0}\mathscr{A}} \right)}^{\rm{T}}}}&{{{\left( {\left( {{X_i} - {X_0}} \right)\mathscr{A}} \right)}^{\rm{T}}} + \mathscr{B}{H_i}}\\
* &{ - {{\rm{H}}_{\rm{i}}} - {\rm{H}}_{\rm{i}}^T}
\end{array}} \right] < 0,
$
|
(22) |
then it holds that
|
$
{{\mathit{\tilde \Xi }}_i} + \mathscr{B}{X_0}\mathscr{A} + {\left( {\mathscr{B}{X_0}\mathscr{A}} \right)^{\rm{T}}} < 0,i = 1, \cdots ,p.
$
|
(23) |
Lemma 2 [30] For any n×n matrices X>0, U, scalar ε>0, the following matrix inequality holds:
|
$
U{X^{ - 1}}{U^{\rm{T}}} \ge \varepsilon \left( {U + {U^{\rm{T}}}} \right) - {\varepsilon ^2}X.
$
|
Theorem 3 Given the detected delay of switching signal δ, consider the Markovian jump system (14).If for some prescribed positive scalars κi and εli, there exist matrices 0 < Xi∈ Rn×n, Ki∈ Rn×n0, X0∈ Rn×n, and positive scalars βi, ξl, αli, and ci, j, i, j∈$\mathscr{M}$, j≠ i, l=1, 2 such that (13) and the following LMIs hold:
|
$
{{\bar \beta }_i}I \le {X_i},
$
|
(24) |
|
$
\begin{array}{l}
{\mathit{\Xi }_i} \buildrel \Delta \over = \\
\left[ {\begin{array}{*{20}{c}}
{{{\mathit{\bar \Phi }}_i}}&0&{{\Gamma _i}}&{{A_{0,i}}{{\bar \alpha }_{1i}}}&{{A_{1,i}}{{\bar \alpha }_{2i}}}&{{X_i}{\mathscr{G}_i}}&{{X_i}{\mathscr{R}_i}}\\
* &{{{\mathit{\bar \Psi }}_i}}&0&0&0&0&0\\
*&* &{ - {\varepsilon _{1i}}\left( {{X_0} + X_0^{\rm{T}}} \right)}&0&0&0&0\\
*&*&* &{ - {{\bar \alpha }_{1i}}I}&0&0&0\\
*&*&*&* &{ - {{\bar \alpha }_{2i}}I}&0&0\\
*&*&*&*&* &{ - {\Lambda _i}}&0\\
*&*&*&*&*&* &{ - \chi }
\end{array}} \right] < 0,
\end{array}
$
|
(25) |
|
$
\left[ {\begin{array}{*{20}{c}}
{{\mathit{\Omega }_{ij}}}&{{X_i} - X_0^{\rm{T}} + {\varepsilon _{2i}}{B_i}\left( {{{\bar K}_j} - {{\bar K}_i}} \right)}\\
* &{ - {\varepsilon _{2i}}\left( {{X_0} + X_0^{\rm{T}}} \right)}
\end{array}} \right] < 0,j \ne i,
$
|
(26) |
|
$
\left[ {\begin{array}{*{20}{c}}
{ - {{\bar \xi }_1}}&{{{\bar \xi }_1}}&{{{\bar \xi }_1}\Upsilon }\\
* &{ - {{\bar \xi }_2}}&0\\
*&* &{ - \mathscr{Y}}
\end{array}} \right] < 0,
$
|
(27) |
where
|
$
\begin{array}{l}
{{\mathit{\bar \Phi }}_i} = {C_i}{X_i} + {X_i}C_i^{\rm{T}} + {B_i}{{\bar K}_i} + \bar K_i^{\rm{T}}B_i^{\rm{T}} + {\pi _{ii}}{X_i},{\Gamma _i} = \\
{X_i} - X_0^{\rm{T}} + {\varepsilon _{1i}}{B_i}{{\bar K}_i},
\end{array}
$
|
|
$
{{\mathit{\bar \Psi }}_i} = \left[ {\begin{array}{*{20}{c}}
{ - {{\bar \xi }_2}I}&{{{\bar \xi }_2}L_i^{\rm{T}}}&{{{\bar \xi }_2}\bar G_{2i}^{\rm{T}}}\\
* &{ - {{\bar \alpha }_{2i}}I}&0\\
*&* &{ - {{\bar \beta }_i}I}
\end{array}} \right],
$
|
|
$
{\mathscr{G}_i} = \left[ {\begin{array}{*{20}{c}}
{\bar G_{1i}^{\rm{T}}}&{L_i^{\rm{T}}}&I
\end{array}} \right],{\Lambda _i} = {\rm{diag}}\left( {{{\bar \beta }_i}I,{{\bar \alpha }_{1i}}I,{{\bar \xi }_1}} \right),
$
|
|
$
\chi = {\rm{diag}}\left( {{X_1}, \cdots ,{X_{i - 1}},{X_{i + 1}}, \cdots ,{X_N}} \right),
$
|
|
$
\gamma = \left[ {\begin{array}{*{20}{c}}
{{\mathscr{P}_1}}& \cdots &{{\mathscr{P}_i}}& \cdots &{{\mathscr{P}_N}}
\end{array}} \right],
$
|
|
$
\begin{array}{l}
{\Upsilon _i} = \left[ {\begin{array}{*{20}{c}}
{\sqrt {{\pi _{i1}}} }& \cdots &{\sqrt {{\pi _{i,i - 1}}} }&{\sqrt {{\pi _{i,i + 1}}} }& \cdots
\end{array}} \right.\\
\sqrt {{\pi _{iN}}} ,
\end{array}
$
|
|
$
\begin{array}{l}
{\mathscr{P}_i} = \left[ {\begin{array}{*{20}{c}}
{\sqrt {{P_{1,i}}\left( \delta \right)} }& \cdots &{\sqrt {{P_{i - 1,i}}\left( \delta \right)} }&{\sqrt {{P_{i + 1,i}}\left( \delta \right)} }& \cdots
\end{array}} \right.\\
\left. {\sqrt {{{\rm{P}}_{N,i}}\left( \delta \right)} } \right],
\end{array}
$
|
|
$
\begin{array}{l}
\mathscr{Y} = {\rm{diag}}\left( {{y_1},{y_2}, \cdots ,{y_N}} \right),{y_i} = {\rm{diag}}\left( {{{\bar c}_{i,1}}, \cdots ,{{\bar c}_{i,i - 1}},} \right.\\
\left. {{{\bar c}_{i,i + 1}}, \cdots ,{{\bar c}_{i,N}}} \right),
\end{array}
$
|
|
$
{\mathit{\Omega }_{ij}} = - 2{\kappa _i}{X_i} + \kappa _i^2{{\bar c}_{ij}}I + B\left( {{{\bar K}_j} - {{\bar K}_i}} \right) + \left( {\bar K_j^{\rm{T}} - \bar K_i^{\rm{T}}} \right)B_i^{\rm{T}},
$
|
then the admissible controller (15) with Ki=KiX0-1 is mean-square exponentially stabilized system (14).
Proof Define Pi=Xi-1, Ki=KiX0, βi= βi-1, αli= αli-1, ξl= ξl-1, i∈ $\mathscr{M}$, l=1, 2.It is easy to verify that (24) and (27) are equivalent to (16) and (13), respectively.Applying Schur complement and Lemma 1, the matrix inequality (25) implies
|
$
{{\mathit{\hat \Xi }}_i} \buildrel \Delta \over = \left[ {\begin{array}{*{20}{c}}
{{{\mathit{\hat \Phi }}_i}}&0&{{A_{0,i}}{{\bar \alpha }_{1i}}}&{{A_{1,i}}{{\bar \alpha }_{2i}}}\\
* &{{{\mathit{\hat \Psi }}_i}}&0&0\\
*&* &{ - {{\bar \alpha }_{1i}}I}&0\\
*&*&* &{ - {{\bar \alpha }_{2i}}I}
\end{array}} \right] < 0,i \in \mathscr{M},
$
|
(28) |
where ${{{\mathit{\hat{\Phi }}}}_{i}}$=(Ci+BiKi)Xi+Xi(Ci+BiKi)T+XiβiG1iXi+Xiα1iLiTLiXi+Xiξ1Xi+ $\sum\nolimits_{j=1}^{N}{{{\pi }_{ij}}}$XiPjXi, ${{{\mathit{\hat{\Psi }}}}_{i}}$=-ξ2I+ξ2βi G2iξ2+ξ2α1iLiTLiξ2.Then pre-and post-multiplying the both sides of (28) by diag {Pi, ξ2I, α1iI, α2iI}, (28) is changed equivalently to (17).
Furthermore, applying Lemma 1 again, and the inequalities -ci, jXiXi≤-2κiXi+κi2ci, jI which is derived from Lemma 2 to (26), we obtain
|
$
\begin{array}{l}
{B_i}\left( {{K_j} - {K_i}} \right){X_i} + {X_i}\left( {K_j^{\rm{T}} - K_i^{\rm{T}}} \right)B_i^{\rm{T}} - \\
{c_{i,j}}{X_i}{X_i} < 0.
\end{array}
$
|
Multiplying the above inequality to the left and the right by Pi yields (18).
4 Numerical examples Example 1 Consider the dynamic reliability problem of multiplexed control system[31]:
|
$
{\rm{Controller}}\;1:{{\dot x}_1} = {u_1},
$
|
|
$
\;\;\;\;\;\;\;{\rm{Plant}}:{{\dot x}_2} = 1.5{x_1} + {a_{22}}{x_2} + 1.5{x_3},
$
|
|
$
{\rm{Controller}}\;2:{{\dot x}_3} = {u_2},
$
|
where a22=0, and u1=-k1x1-k2x2, u2=-k2x2-k1x3.In practice, the controllers may be failure which need to maintenance.Therefore, it is assumed that the failure rate is λ and the repair rate is μ(>λ), and the failure process and the repair process are both exponentially distributed.Then the system can be modeled as (14) with following parameters (see [31-32]):
|
$
{C_1} = \left[ {\begin{array}{*{20}{c}}
0&0&0\\
{1.5}&0&{1.5}\\
0&0&0
\end{array}} \right],{K_1} = - \left[ {\begin{array}{*{20}{c}}
{{k_1}}&{{k_2}}&0\\
0&{{k_2}}&{{k_1}}
\end{array}} \right],
$
|
|
$
{C_2} = \left[ {\begin{array}{*{20}{c}}
0&0&0\\
0&0&{1.5}\\
0&0&0
\end{array}} \right],{K_2} = - \left[ {\begin{array}{*{20}{c}}
{{k_1}}&0&0\\
0&{{k_2}}&{{k_1}}
\end{array}} \right],
$
|
|
$
{C_3} = \left[ {\begin{array}{*{20}{c}}
0&0&0\\
{1.5}&0&0\\
0&0&0
\end{array}} \right],{K_3} = - \left[ {\begin{array}{*{20}{c}}
{{k_1}}&{{k_2}}&0\\
0&0&{{k_1}}
\end{array}} \right],
$
|
|
$
{C_4} = \left[ {\begin{array}{*{20}{c}}
0&0&0\\
0&0&0\\
0&0&0
\end{array}} \right],{K_4} = - \left[ {\begin{array}{*{20}{c}}
{{k_1}}&0&0\\
0&0&{{k_1}}
\end{array}} \right],{B_i} = \left[ {\begin{array}{*{20}{c}}
1&0\\
0&0\\
0&1
\end{array}} \right],
$
|
|
$
{f_i} = 0,{g_i} = 0,i = 1,2,3,4,
$
|
where the first mode corresponds to the case where both controllers are good, and the second and third modes correspond to the case where one of the controllers fails, and the fourth mode corresponds to the case where both controllers are failure.The failure process and the repair process form a Markov chain with generator
|
$
\Pi = \left[ {\begin{array}{*{20}{c}}
{ - 2\lambda }&\lambda &\lambda &0\\
\mu &{ - \left( {\lambda + \mu } \right)}&0&\lambda \\
\mu &0&{ - \left( {\lambda + \mu } \right)}&\lambda \\
0&\mu &\mu &{ - 2\mu }
\end{array}} \right].
$
|
The authors of [17] showed that when λ=0.4, μ=0.55, k1=2.85 and k2=0.33, the synchronous state feedback controller u(t)=Kσ(t)x(t) stabilized the system in mean square.Here, we are interested in that how large detected delay of the controller can be tolerate to preserve the stability of the system.
Applying Theorem 2 with the same gain matrices and Markov generator, it has been found that maximum mode delay δ is 0.61.By using the Euler-Maruyama method[33] with step size 0.001 and setting initial value σ0=3, φ(s)=[-1, -0.3, 0.5]T, the time response of the system is depicted in Fig. 1.Observe that the asynchronous switching controller with δ=0.61 can guarantee the stability of the system.
Furthermore, in order to show the effect of the maximum delay of asynchronous Markovian switching on the stability clearly, assigning that λ=0.4π0, μ=0.55π0, k1=2.85 and k2=0.33, then for different values of π0, we calculate the maximum values of the delay δ.The results are listed in Table 1.It can be seen from the table that when the Markov switching is slowly switching, the admissible delay of asynchronous switching is large, otherwise, the allowable delay is relatively small.This is consistent with our intuition.Next, assume that k1=k2=k, we compute the minimum control intensity k for various δ.From Table 2, the calculation results show that the control intensity increases with the increase of the delay of asynchronous switching.
表 1(Table 1)
Table 1 The maximum values of δ for different π0
| π0 | δ |
| 0.1 | 5.72 |
| 0.3 | 1.95 |
| 0.7 | 0.86 |
| 1.0 | 0.61 |
| 1.6 | 0.39 |
| 2.0 | 0.31 |
| 3.0 | 0.21 |
| 5.0 | 0.13 |
|
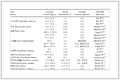 |
Table 1 The maximum values of δ for different π0
|
表 2(Table 2)
Table 2 The minimum values of k(k1=k2) for different δ
| δ | k |
| 0.05 | 0.09 |
| 0.10 | 0.21 |
| 0.15 | 0.36 |
| 0.20 | 0.57 |
| 0.25 | 0.93 |
| 0.30 | 1.70 |
| 0.35 | 5.48 |
| 0.40 | - |
|
 |
Table 2 The minimum values of k(k1=k2) for different δ
|
Example 2 Consider a two dimensional switched system (14) with following parameters
|
$
{C_1} = \left[ {\begin{array}{*{20}{c}}
{2.33}&{ - 1}\\
3&{ - 4.92}
\end{array}} \right],{A_{01}} = 0,
$
|
|
$
{A_{11}} = \left[ {\begin{array}{*{20}{c}}
{0.25}&{0.16}\\
{ - 0.2}&{0.51}
\end{array}} \right],{B_1} = \left[ {\begin{array}{*{20}{c}}
1\\
0
\end{array}} \right].
$
|
|
$
{{\bar G}_{11}} = \left[ {\begin{array}{*{20}{c}}
{0.51}&{1.23}\\
{0.46}&{ - 0.4}
\end{array}} \right],{C_2} = \left[ {\begin{array}{*{20}{c}}
{ - 1}&1\\
{ - 2}&5
\end{array}} \right],{A_{02}} = 0,
$
|
|
$
{A_{12}} = \left[ {\begin{array}{*{20}{c}}
{0.1}&{ - 0.3}\\
{0.27}&{0.18}
\end{array}} \right],
$
|
|
$
{B_2} = \left[ {\begin{array}{*{20}{c}}
0\\
1
\end{array}} \right],{{\bar G}_{12}} = \left[ {\begin{array}{*{20}{c}}
{0.21}&{0.43}\\
{0.40}&{ - 0.22}
\end{array}} \right],
$
|
|
$
\Pi = \left[ {\begin{array}{*{20}{c}}
{ - 1}&1\\
1&{ - 1}
\end{array}} \right],
$
|
fi(x, t)=x, gi(x, y, t)=G1ix, i=1, 2, and the time delay of asynchronous switching δ=0.1.This hybrid stochastic system is not mean-square exponentially stable without control input.Our purpose is to design a mode-dependent state-feedback controller (14) to stabilize the system with any constant state delay.Therefore, applying Theorem 3 with the choices of κ1=18, κ2=12, ε11=0.06, ε21=0.05, ε12=ε22=0.01, it has been found that LMIs (24)-(27) are feasible, and the corresponding control gain matrices are
|
$
{K_1} = \left[ {\begin{array}{*{20}{c}}
{ - 7.67}&{ - 3.39}
\end{array}} \right],{K_2} = \left[ {\begin{array}{*{20}{c}}
{0.75}&{ - 7.56}
\end{array}} \right].
$
|
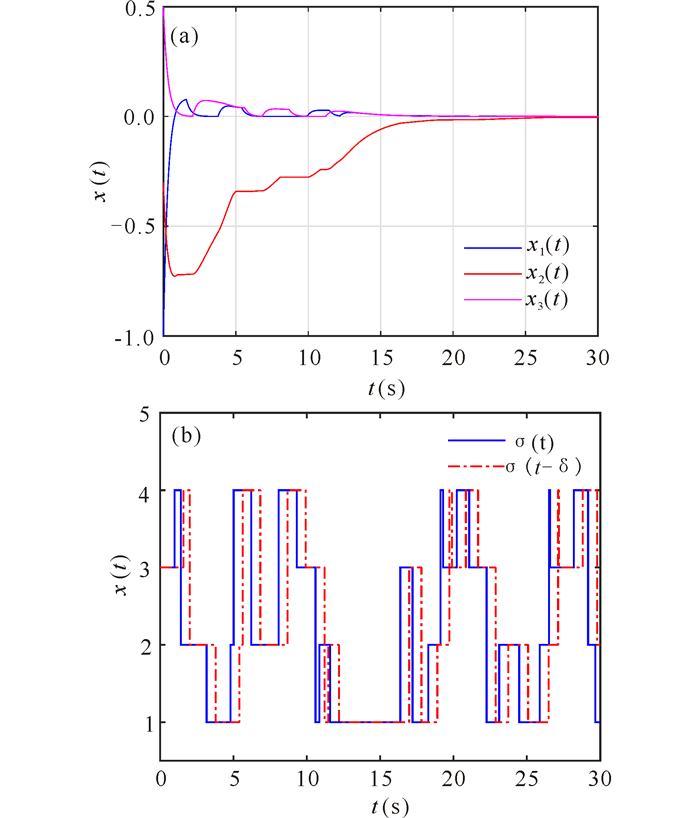
For simulation studies, we use the Euler-Maruyama method[33] with step size 0.001 and initial values σ0=1, φ(s)=[4, -3]T, s∈[-τ, 0].Then, the sample path of the solution is plotted in Fig. 2a-b for τ=1 and τ=10, respectively.The corresponding switching signal is also given in Fig. 2c. It is seen that the asynchronous switching controller (14) with gain matrices (29) indeed asymptotically stabilizes the system with different delays.
5 Conclusion By exploring the relationship between the sizes of detected delay of switching signal and the generator of the Markov chain, a novel integral-inequality-estimation technique is developed to deal with time-varying delay, and some state-delay-independent stability criteria have been established for hybrid stochastic retarded systems with asynchronous Markovian switching.It has shown that if the synchronous switched controlled system is pth-moment exponentially stable, then sufficiently small delays of asynchronous switching will not destroy the stability of the system.Compared with some existing results on the synchronous switching, our Theorem 1 does not impose any restriction on the derivative of state delay.As its application, the obtained results have been applied to design stabilizing mode-dependent controller for a class of time-delay stochastic systems under asynchronous Markovian switching.Simulation results have verified the effectiveness of the theoretical results.

 2017, Vol. 24
2017, Vol. 24 


