Swarm intelligence optimization algorithm originates from the simulation of various types of biological behavior in nature and has characteristics of simple operation, good optimization performance and strong robustness.Inspired by this idea, there are many bio-inspired swarm intelligent optimization algorithms are proposed, such as, ant colony optimization (ACO)[1], differential evolution (DE)[2], particle swarm optimization (PSO)[3], firefly algorithm (FA)[4], glowworm swarm optimization (GSO)[5], monkey search (MS)[6], harmony search (HS)[7], cuckoo search (CS)[8], bat algorithm (BA)[9], et al.Swarm intelligence optimization algorithm can solve problems which traditional methods cannot handle effectively and it has shown excellent performance in many respects, and its application scope has been greatly expanded.
The social-spider optimization algorithm is proposed by Erik Cuevas in 2013[10], it is a novel metaheuristic optimization algorithm by simulating social-spider behavior.Social-spiders are a representative example of social insects[11].A social-spider is a spider species whose members maintain a set of complex cooperative behaviors[12].Whereas most spiders are solitary and even aggressive toward other members of their own species, social-spiders show a tendency to live in groups, forming long-lasting aggregations often referred to as colonies[13].In a social-spider colony, each member, depending on its gender, executes a variety of tasks such as predation, mating, web design, and social interaction[13-14].The web is an important part of the colony because it is not only used as a common environment for all members, but also as a communication channel[15] among them.Therefore, important information (such as trapped prays or mating possibilities) is transmitted by small vibrations through the web.Such information, considered as a local knowledge, is employed by each member to conduct its own cooperative behavior, influencing simultaneously the social regulation of the colony[16].The SSO algorithm is based on the simulation of the cooperative behavior of social-spiders.In SSO algorithm, individuals emulate a group of spiders which interact to each other based on the biological laws of the cooperative colony.The algorithm is divided into two different search agents (spiders):Males and females.Depending on gender, each individual is conducted by a set of different evolutionary operators which mimic different cooperative behaviors which are typical in a colony.Different to most of existent swarm algorithms, most of swarm algorithms model individuals as unisex entities that perform virtually the same behavior.Under such circumstances, algorithms waste the possibility of adding new and selective operators as a result of considering individuals with different characteristics such as sex, task-responsibility, etc.These operators could incorporate computational mechanisms to improve several important algorithm characteristics including population diversity and searching capacities.
In this paper, a social-spider optimization algorithm with differential mutation operator (SSO-DM) has been applied to functions optimization.The improvement involves differential mutation operator.Differential mutation operator enhances the convergence speed and computational accuracy of the algorithm.A social-spider optimization algorithm with differential mutation operator is validated by 5 benchmark functions.The results show that the proposed algorithm is able to obtained accurate solution, and it also has a fast convergence speed and a high degree of stability.
1 The SSO algorithmThe SSO assumes that entire search space is a communal web, where all the social-spiders interact to each other.In this approach, each solution within the search space represents a spider position in the communal web.Every spider receives a weight according to the fitness value of the solution that is symbolized by the social-spider.The algorithm is divided into two different search agents (spiders):Males and females.Depending on gender, each individual is conducted by a set of different evolutionary operators which mimic different cooperative behaviors that are commonly assumed within the colony.
An interesting characteristic of social-spiders is the highly female-biased populations.In order to emulate this fact, the algorithm starts by defining the number of female and male spiders that will be characterized as individuals in the search space.The number of females (Nf) is randomly selected within the range of 65%-90% of the entire population (N).So, Nf is calculated by the following equation:
| ${{N}_{f}}=floor[\left( 0.9-rand*0.25 \right)*N]$ | (1) |
Where rand is a random number between [0, 1], whereas floor(.) maps a real number to an integer number.The number of male spiders (Nm) is computed as the complement between N and Nf.It is calculated as follows:
| ${{N}_{m}}=N-{{N}_{f}}.$ | (2) |
The group F stands for female population (F={f1, f2, …, fNf}), the group M stands for male population (M={m1, m2, …, mNm}) and the group S stands for entire population, such that S=F∪M.
1.1 Fitness assignationIn the biological metaphor, the spider size is the characteristic that evaluates the individual capacity to perform better over its assigned tasks.In this approach, every individual (spider) receives a weight (wi) which represents the solution quality that corresponds to the spider (i) of the population (S).In order to calculate the weight of every spider the next equation is used:
| ${{w}_{i}}=\frac{J\left( {{s}_{i}} \right)-wors{{t}_{s}}}{~bes{{t}_{s}}-wors{{t}_{s}}},$ | (3) |
Where J(si) is the objective function value of the social-spider individual (si).The values of worsts and bests are defined as:
| $bes{{t}_{s}}=\underset{k\in \left\{ 1,\text{ }2,\cdots ,\text{ }N \right\}}{\mathop{\text{max}~\left( J\left( {{s}_{k}} \right) \right)}}\,\text{and}\ wors{{t}_{s}}=\underset{k\in \left\{ 1,\text{ }2,\cdots ,N \right\}}{\mathop{\text{min}~\left( J\left( {{s}_{k}} \right) \right)}}\,.$ | (4) |
The communal web is used as a mechanism to transmit information among the colony members.This information is encoded as small vibrations that are critical for the collective coordination of all individuals in the population.The vibrations depend on the weight and distance of the spider which has generated them.Since the distance is relative to the individual that provokes the vibrations and the member who detects them, members located near to the individual that provokes the vibrations, perceive stronger vibrations in comparison with members located in distant positions.In order to reproduce this process, the vibrations perceived by the individual i as a result of the information transmitted by the member j are modeled according to the following equation:
| $Vi{{b}_{i,\text{ }j}}={{w}_{j}}*{{e}^{-d_{i,\text{ }j}^{2}}},$ | (5) |
Where di, j is the Euclidian distance between the spiders i and j, such that di, j=‖si-sj‖. Although it is virtually possible to compute perceived vibrations by considering any pair of individuals, three special relationships are considered within the SSO approach:
① Vibrations (Vibci) are perceived by the individual i(si) as a result of the information transmitted by the member c(sc) who is an individual that has two characteristics:It is the nearest member to i and possesses a higher weight in comparison to i (wc > wi).
| $Vib{{c}_{i}}={{w}_{c}}*{{e}^{-d_{i,\text{ }c}^{2}}}.$ | (6) |
② Vibrations (Vibbi) perceived by the individual i as a result of the information transmitted by the member b (sb), with b being the individual holding the best weight (best fitness value) of the entire population S, such that
| $Vib{{b}_{i}}={{w}_{b}}*{{e}^{-d_{i,\text{ }b}^{2}}}.$ | (7) |
③ Vibrations (Vibfi) perceived by the individual i(si) as a result of the information transmitted by the member f(sf), with f being the nearest female individual to i.
| $Vib{{f}_{i}}={{w}_{f}}*{{e}^{-d_{i,\text{ }f}^{2}}}.$ | (8) |
The SSO is an iterative process whose first step is to randomly initialize the entire population (female and male).The algorithm begins by initializing the set S of N spider positions.Each spider position, fi or mi, is an n-dimensional vector containing the parameter values to be optimized.Such values are randomly and uniformly distributed between the pre-specified lower initial parameter bound (pjlow) and the upper initial parameter bound (pjhigh), just as it is described by the following expressions:
| $f_{i,\text{ }j}^{0}=p_{j}^{low}+\underset{k=1,\text{ }2,\cdots ,{{N}_{m}};j=1,\text{ }2,\cdots ,n}{\mathop{rand\left( 0,\text{ }1 \right)*\left( p_{j}^{high}-p_{j}^{low} \right)}}\,,m_{k,\text{ }j}^{0}=p_{j}^{low}+\underset{k=1,2,\cdots ,\text{ }{{N}_{m}};j=1,2,\cdots ,n}{\mathop{rand\left( 0,\text{ }1 \right)*\left( p_{j}^{high}-p_{j}^{low} \right)}}\,.$ | (9) |
Where i, j and k are the parameter and individual indexes respectively whereas zero signals the initial population.The function rand(0, 1) generates a random number between 0 and 1.
1.4 Cooperative operators 1.4.1 Female cooperative operatorIn order to emulate the cooperative behavior of the female spider, a new operator is defined.The operator considers the position change of the female spider i at each iteration process.Such position change, which can be of attraction or repulsion, is computed as a combination of three different elements.The first one involves the change in regard to the nearest member to i that holds a higher weight and produces the vibration (Vibci).The second one considers the change regarding the best individual of the entire population (S) who produces the vibration (Vibbi).Finally, the third one incorporates a random movement.
Since the final movement of attraction or repulsion depends on several random phenomena, the selection is modeled as a stochastic decision.For this operation, a uniform random number (rm) is generated within the range [0, 1].If rm is smaller than a threshold (PF), an attraction movement is generated; otherwise, a repulsion movement is produced.Therefore, such operator can be modeled as follows:
| $f_{i}^{k+1}=\left\{ \begin{array}{*{35}{l}} f_{i}^{k}+\alpha *Vib{{c}_{i}}*\left( {{s}_{c}}-f_{i}^{k} \right)+\beta *Vib{{b}_{i}}*\left( {{s}_{b}}-f_{i}^{k} \right)+ \\ \quad \quad \delta *\left( rand-\frac{1}{2} \right);{{r}_{m}}<PF \\ f_{i}^{k}-\alpha *Vib{{c}_{i}}*\left( {{s}_{c}}-f_{i}^{k} \right)-\beta *Vib{{b}_{i}}*({{s}_{b}}- \\ \quad \quad f_{i}^{k})+\delta *\left( rand-\frac{1}{2} \right);{{r}_{m}}>PF \\ \end{array} \right..$ | (10) |
Where α, β, δ and rand are random numbers between [0, 1], whereas k represents the iteration number.The individual sc and ss represent the nearest member to i that holds a higher weight and the entire population (S), respectively.
Under this operation, each particle presents a movement which combines the past position that holds the attraction or repulsion vector over the local best element (sc) and the global best individual (sb) seen so-far.This particular type of interaction avoids the quick concentration of particles at only one point and encourages each particle to search around the local candidate region within its neighborhood (sc), rather than interacting to a particle (sb) in a distant region of the domain.The use of this scheme has two advantages.First, it prevents the particles from moving towards the global best position, making the algorithm less susceptible to premature convergence.Second, it encourages particles to explore their own neighborhood thoroughly before converging towards the global best position.
1.4.2 Male cooperative operatorAccording to the biological behavior of the social-spider, male population is divided into two classes:Dominant and non-dominant male spiders.Dominant male spiders have better fitness characteristics (usually regarding the size) in comparison to non-dominant.Dominant males are attracted to the closest female spider in the communal web.In contrast, non-dominant male spiders tend to concentrate on the center of the male population as a strategy to take advantage of resources that are wasted by dominant males.
For emulating such cooperative behavior, the male members are divided into two different groups (dominant members D and non-dominant members ND) according to their position with regard to the median member.Male members, with a weight value above the median value within the male population, are considered the dominant individuals (D).On the other hand, those under the median value are labeled as non-dominant males (ND).In order to implement such computation, the male population (M={m1, m2, …, mNm}) is arranged according to their weight value in decreasing order.Thus, the individual whose weight (wNf+m) is located in the middle is considered the median male member.Since indexes of the male population in regard to the entire population are increased by the number of female members (Nf), the median weight is indexed by (Nf+m).According to this, change of positions for the male spider can be modeled as follows:
| $m_{i}^{k+1}=\left\{ \begin{array}{*{35}{l}} m_{i}^{k}+\alpha *Vib{{f}_{i}}*\left( {{s}_{f}}-m_{i}^{k} \right)+\delta *\left( rand-\frac{1}{2} \right) \\ \quad \quad {{w}_{{{N}_{f+i}}}}>{{w}_{{{N}_{f+m}}}}; \\ mw_{i}^{k}+\alpha *(\frac{\sum\nolimits_{h=1}^{{{N}_{m}}}{m_{h}^{k}}*{{w}_{{{N}_{f+h}}}}}{\sum\nolimits_{h=1}^{{{N}_{m}}}{{{w}_{{{N}_{f+h}}}}}}~-m_{i}^{k}) \\ \quad \quad {{w}_{{{N}_{f+i}}}}\le {{w}_{{{N}_{f+m}}}}. \\ \end{array} \right.$ | (11) |
Where the individual (sf) represents the nearest female individual to the male member i, whereas (
In SSO algorithm, Dominant members (D) and female spiders perform the mating operation.Each male spider has a specific mating radius (r), which is defined as:
| $r=\frac{\sum\limits_{j=1}^{n}{p_{j}^{high}-p_{j}^{low}}~}{2n}.$ | (12) |
During mating, the weight of spiders involved in mating that can affact the quality of the next generation of spiders.The influence probability (Psi) of each spider is assigned by the roulette method, which is defined as follows:
| $P{{s}_{i}}=\frac{{{w}_{i}}}{\sum\limits_{j\in {{T}^{g}}}{{{w}_{j}}}}.$ | (13) |
If the weight of the newly formed spider is greater than the lightest spider of the previous spider population, the new spider will replace the lightest spider in the spider population.Instead, the new spider will be abandoned and the spider population will not change.
1.6 Computational procedureThe computational procedure for the algorithm can be summarized as follow:
The Social-spider optimization algorithm (SSO)
Step 1:Think N as the total number of n-dimensional colony members, define the number of male spiders (Nm) and female spiders (Nf) in the entire population (S).
Nf=floor[(0.9-rand*0.25)*N], Nm=N-Nf,
Where rand is a random number between [0, 1], whereas floor(.) maps a real number to an integer number.
Step 2:Initialize randomly the female (F={f1, f2, …, fNf}), male (M={m1, m2, …, mNm}) members (where S={s1=f1, s2=f2, …, sNf=fNf, sNf+1= m1, sNf+2=m2, …, SN=mNm}) and calculate the radius of mating.
| $r=\frac{\sum\limits_{j=1}^{n}{p_{j}^{high}-p_{j}^{low}}}{2n}.$ |
Step 3:Calculate the weight of every spider of S.
For (i=1;i < N+1;i++)
End for
Step 4:Female spider's movement according to the female cooperative operator.
For (i=1;i < Nf+1;i++)
Calculate Vibci and Vibbi
If (rm < PF); where rm∈rand(0, 1)
| $\begin{align} & \quad \ \quad \ f_{i}^{k+1}=f_{i}^{k}+\alpha *Vib{{c}_{i}}*\left( {{s}_{c}}-f_{i}^{k} \right)+ \\ & \beta *Vib{{b}_{i}}*\left( {{s}_{b}}-f_{i}^{k} \right)+\delta *\left( rand-\frac{1}{2} \right), \\ \end{align}$ |
Else if
| $\begin{align} & \quad \quad \quad \quad f_{i}^{k+1}=f_{i}^{k}\alpha *Vib{{c}_{i}}*\left( {{s}_{c}}-f_{i}^{k} \right)- \\ & \beta *Vib{{b}_{i}}*\left( {{s}_{b}}-f_{i}^{k} \right)+\delta *\left( rand-\frac{1}{2} \right), \\ \end{align}$ |
End if
End for
Step 5:Move the male spiders according to the male cooperative operator.
Find the median male individual (wNf+m) from M.
For (i=1;i < Nm+1;i++)
Calculate Vibfi
If (wNf+i > wNf+m)
mik+1=mik+α*Vibfi*(sf-mik)+δ*
(rand-
Else if
| $m_{i}^{k+1}=m_{i}^{k}+\alpha *(\frac{\sum _{h=1}^{{{N}_{m}}}m_{h}^{k}*{{w}_{{{N}_{f}}+h}}~}{\sum _{h=1}^{{{N}_{m}}}{{w}_{{{N}_{f}}+h}}}~-m_{i}^{k}),$ |
End If
End for
Step 6:Perform the mating operation
For (i =1;i < Nm+1;i++)
If (mi∈D)
Find Ei
If (Ei is not empty)
From snew using the roulette
method
If (wnew > wwo)
swo=snew
End If
End if
End if
End for
Step 7:if the stop criteria is met, the process is finished; otherwise, go to Step 3.
2 Differential mutation operator-based social spider optimization algorithm (SSO-DM) 2.1 Differential Mutation operator (DM)The differential evolution (DE) developed by Storn and Price, is a stochastic search algorithm based on population cooperation and competition of individuals and has been successfully applied to solve optimization problems particularly involving non-smooth objective functions[17-22].The optimization process in DE is carried out by combing the simple arithmetic operators with the classical evolution operators of mutation, crossover and selection to evolve from a randomly generated population to a final solution.The differential mutation operation is defined by [23].
| $x_{i}^{k+1}=x_{i}^{k}+\left( 1-Y \right)\times \left( x_{l}^{k}-x_{m}^{k} \right)+Y\times \left( x_{g}^{k}-x_{j}^{k} \right),$ | (14) |
Where j, l, g and m are random integers uniformly selected from the set X={x1, x2, ..., xn} and i≠j≠l≠m≠g, in other word the indices are mutually different.Y is defined by
| $Y=\text{ }\frac{{{k}_{cur}}}{{{k}_{\text{max }\!\!~\!\!\text{ }}}},$ | (15) |
where kcur is the current iteration and kmax is the number of maximum iterations.
2.2 The flight characteristics of social spidersThe flight (ballooning) is properties of many social spiders.Social spiders can achieve rapid diffusion by means of flight behavior at a certain stage.The flight is an important way to realize long distance diffusion of spiders, the flight distance sometimes can reach hundreds of kilometers.This is also the main reason for the rapid spread of social spiders.Inspired by this feature, assume that social spiders sometimes change their position according to this characteristic.
2.3 The necessary properties and theoretical analysis of the SSO-DM algorithm(A)The necessary properties (The flight characteristics of social spiders)
The article uses differential mutation operator to simulate the flight characteristics of social spiders.Suppose that each female social spider has flight characteristic, the calculation formula of the position change of the flying characteristic of the female social spider is as follows:
| $f_{i}^{k+1}=f_{i}^{k}+\left( 1-Y \right)\times \left( f_{l}^{k}-f_{m}^{k} \right)+Y\times \left( f_{g}^{k}-f_{j}^{k} \right),$ | (16) |
Where j, l, g and m are random integers uniformly selected from the set F={f1, f2, …, fNf} and i≠j≠l≠m≠g, in other word, the indices are mutually different.Y is described in Eq.(15).
Because the flight characteristics of social spiders are shown in a stage, defining a random number-Z and a threshold value-R.Where, Z is a random number between[0, 1], R is a constant with a value of 0.5.When R < Z, female social spiders perform the operation of the flight characteristics, otherwise, female social spiders perform the operation of the original algorithm.
(B)Theoretical analysis of the SSO-DM algorithm
In SSO-DM algorithm, the parameter (Z) that controls variables for the flight characteristics of female social spiders, it always obliges the female social spiders to take random executes the operation of the flight characteristics, which greatly enhances population diversity in the algorithm and promotes exploration of the search space that leads to find diverse solutions during optimization.This mechanism is very helpful for resolving local optima stagnation even when the SSO-DM algorithm is in the exploitation phase.
The proposed SSO-DM consists essentially in a strong co-operation of the two evolutionary algorithms.The main difference with SSO is in the mutation operation.This efficient combination strategy of DM and SSO improves the global search capability, avoiding convergence to local minima and accelerates the convergence.The SSO-DM can be summarized as follow (Fig. 1):
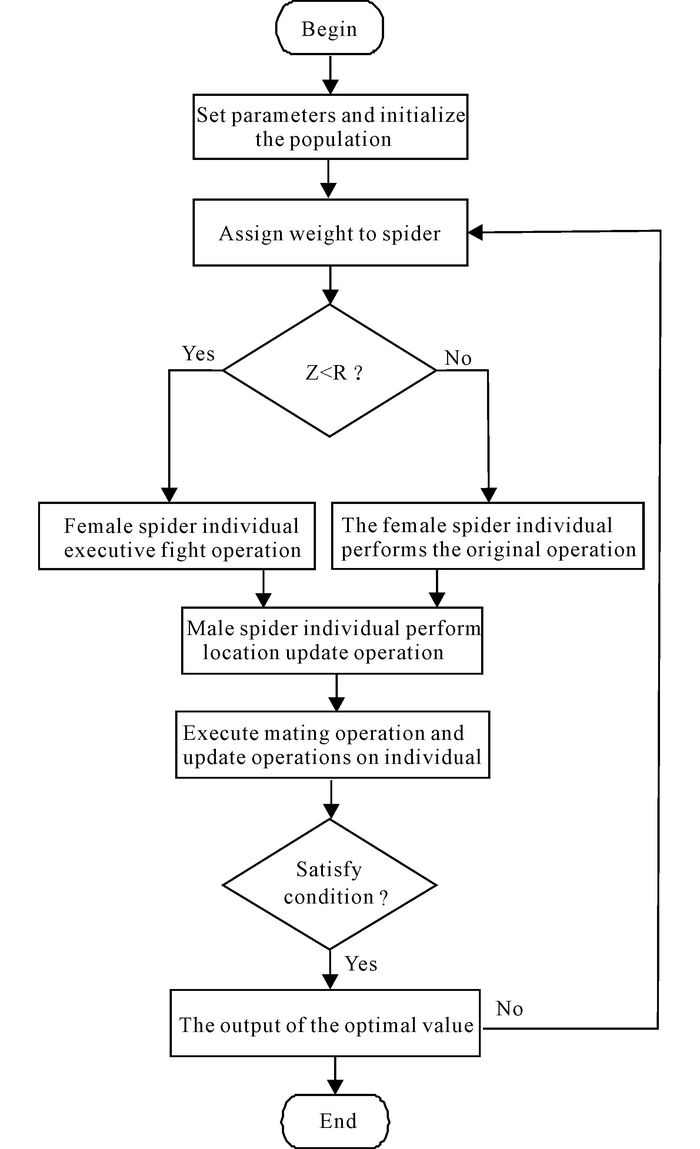
|
Fig.1 The flow chart of SSO-DM algorithm |
Social-spider optimization algorithm with differential mutation operator (SSO-DM)
Step 1-Step 3:The same as the original algorithm.
Step 4:Female spider's movement according to the female cooperative operator.
For (i=1;i < Nf+1;i++)
Calculate Vibci and Vibbi
Create Z as a random number in range (0, 1)
If Z < 0.5
fik+1=fik+(1-Y)×(flk-fmk)+Y×(fgk-fjk),
Else
If (rm < PF); where rm∈rand(0, 1)
fik+1=fik+α*Vibci*(sc-fik)+β*Vibbi*(sb-fik)+δ*(rand-
Else If
fik+1=fik-α*Vibci*(sc-fik)-β*Vibbi*(sb-fik)+δ*(rand-
End If
End If
End For
Step 5-Step 7:The same as the original algorithm.
3 Simulation experiments and result analysisIn this section, five standard test functions[24] are applied to evaluate the optimal performance of SSO-DM.The space dimension, scope and optimal value of five functions are shown in Table 1.The selected benchmark functions can be divided into two categories (i.e., unimodal benchmark functions and multimodal benchmark functions).They are f1~f3 for unimodal benchmark functions, f4 and f5 for multimodal benchmark functions.
| Table 1 Unimodal and multimodal benchmark functions |
All of algorithms were programmed in MATLAB R2012a, numerical experiment was set up on Inter (R) Core(TM) i5-4590 CPU and 4 GB memory.
3.2 Comparison of each algorithm performanceThe proposed SSO-DM algorithm is compared with some swarm intelligence optimization algorithms, such as, SSO, ABC, BA, GGSA and DE, which use the mean and standard deviation to compare their optimal performance.The parameters settings of algorithms are as follows.For all the optimization algorithms, Population size N=50, and the iteration number is 1 000.30 independent runs were made for the six algorithms, the results obtained by six algorithms are presented in Table 2, and the evolution curves and the variance diagram of f1, f2, f3, f4, f5 obtained by six algorithms are presented in Fig. 2—6and Fig. 7—11, respectively.
| Table 2 Simulation results for test unimodal benchmark functions |
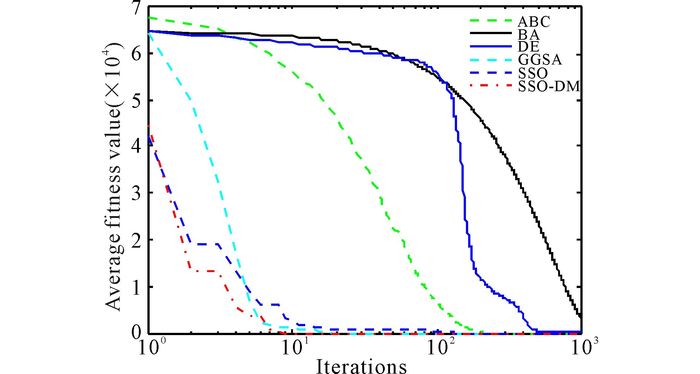
|
Fig.2 Dim=30, evolution curves of fitness value for f1 |
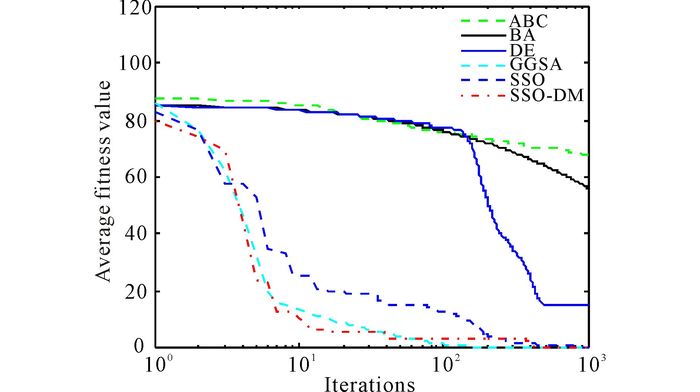
|
Fig.3 Dim=30, evolution curves of fitness value for f2 |
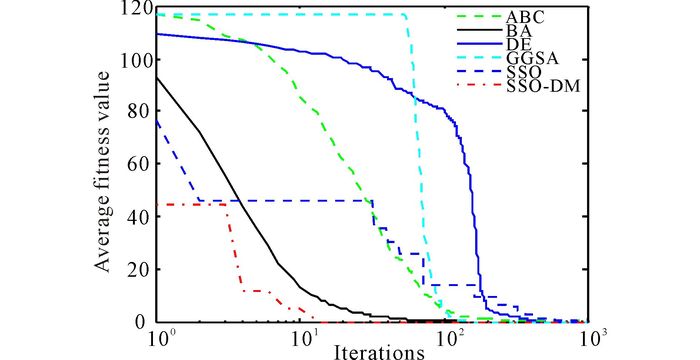
|
Fig.4 Dim=30, evolution curves of fitness value for f3 |
|
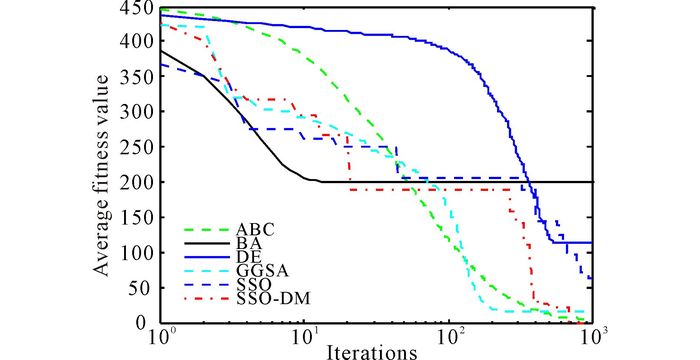
Fig.5 Dim=30, evolution curves of fitness value for f4 |
|
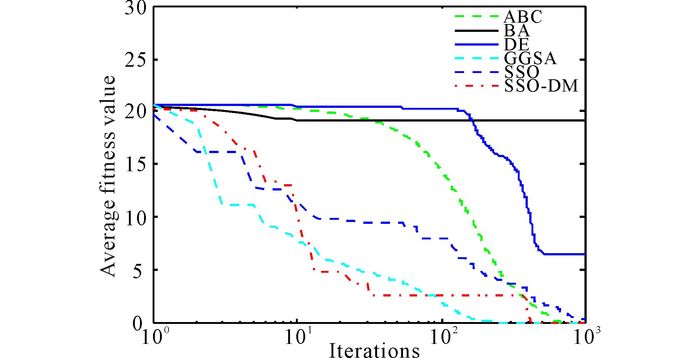
Fig.6 Dim=30, evolution curves of fitness value for f5 |
|
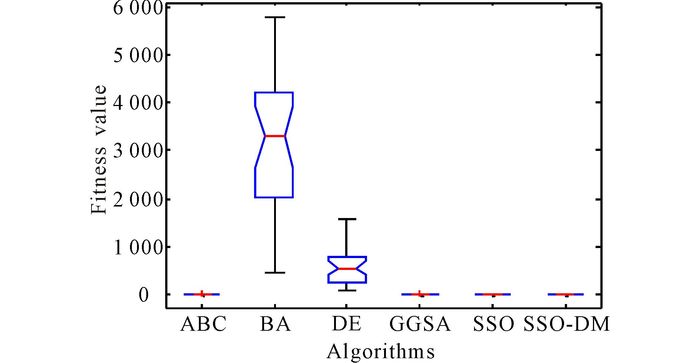
Fig.7 Dim=30, variance diagram of fitness value for f1 |
|
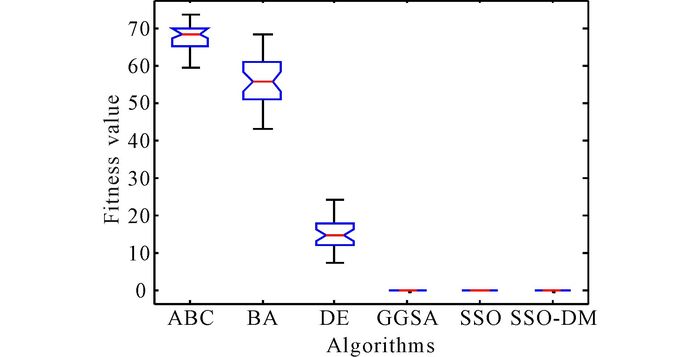
Fig.8 Dim=30, variance diagram of fitness value for f2 |

|
Fig.9 Dim=30, variance diagram of fitness value for f3 |
|
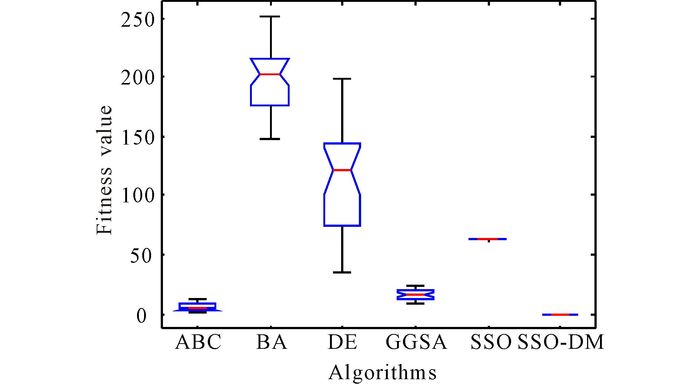
Fig.10 Dim=30, variance diagram of fitness value for f4 |
|
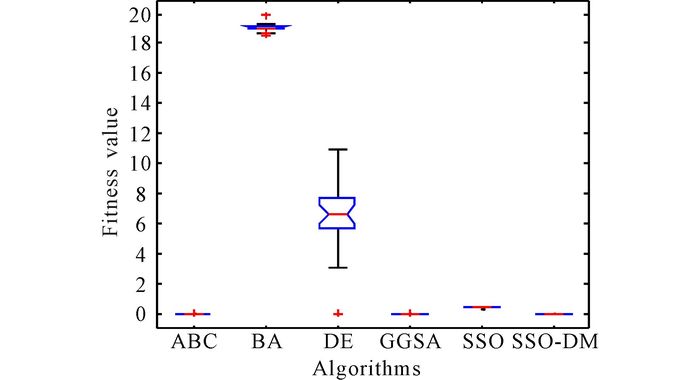
Fig.11 Dim=30, variance diagram of fitness value for f5 |
Seen from Table 2, in unimodal benchmark functions, SSO-DM can get a better optimal solution for f1, f2 and f3 and has a very strong robustness.For the test benchmark functions, standard deviation of SSO-DM is less than that of other algorithm.And this means that in the optimization of unimodal function, SSO-DM has better stability.Similarly, seen from Table 2, SSO-DM can find the optimal solution for f4, and the standard deviations are zeros.For f4, f5, the precision of mean fitness value, best fitness value, worst fitness value and standard deviation of SSO-DM are better than other algorithms.These results mean that SSO-DM has a strong searching ability and a great stability for solving multimodal function optimization.Fig. 2-6 show the evolution curves of fitness value for f1, f2, f3, f4, f5.From these Figs, we can easily find that SSO-DM converges faster than other population based algorithms mentioned above, and the values obtained by SSO-DM are closer to the optimal value of benchmark functions.These show that SSO-DM has a faster convergence speed and a better precision than SSO and other population based algorithms.In sum, proposed SSO-DM is an algorithm with fast convergence speed, high level of precision and a great performance of stability.
Another finding in the results is the poor performance of ABC and BA.These two algorithms belong to the class of swarm-based algorithms.In contrary to SSO-DM algorithm, there is no mechanism for significant abrupt movements in the search space and this is likely to be the reason for the poor performance of ABC and BA.It is also worth discussing the poor performance of the DE algorithm in this subsection.Generally speaking, the DE algorithm has been designed based on mutation mechanism, mutation in evolutionary algorithms maintains the diversity of population and promotes exploitation, but due to the influence of the choice operation, the individual differences will gradually decrease with the increase of the number of iterations, at the same time, the decrease of individual difference also affects the diversity of the variation, which leads to the premature convergence of the algorithm, which is one of the main reasons for the poor performance of DE.
The reason for getting better fitness value provided by the SSO-DM algorithm is that this algorithm is equipped with the parameter (Z) that controls variables for the flight characteristics of female social spiders, it always obliges the female social spiders to take random executes the operation of the flight characteristics.This promotes exploration of the search space that leads to find diverse solutions during optimization.In addition, two thirds of the individuals in the SSO-DM algorithm are devoted to exploration of the search space and the rest to exploitation.This design guarantees the balance between exploration and exploitation.This is also a reason why the proposed algorithm always guides search agents to exploit the most promising regions of the search space, which also assist this algorithm to provide remarkable results.
4 ConclusionsIn order to overcome the disadvantage of standard social-spider optimization algorithm, differential mutation operator has been incorporated into the SSO to generate a social-spider optimization algorithm with differential mutation operator for function optimization.Differential mutation operator enhances the diversity of the population, which helps to improve its exploration ability.From the results of the five benchmark functions, the performance of SSO-DM is better than, or at least comparable with other population-based algorithm mentioned in this paper.SSO-DM has a fast convergence speed, a relatively high degree of stability and it is also much more accurate in precision.
| [1] | SOCHA K, DORIGO M. Ant colony optimization for continuous domains[J]. European Journal of Operational Research, 2008, 185(3):1155–1173. DOI:10.1016/j.ejor.2006.06.046 |
| [2] | STORN R, PRICE K. Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4):341–359. DOI:10.1023/A:1008202821328 |
| [3] | KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Piscataway: IEEE, 1995: 1942-1948. |
| [4] | YANG X S. Multiobjective firefly algorithm for continuous optimization[J]. Engineering with Computers, 2013, 29(2):175–184. DOI:10.1007/s00366-012-0254-1 |
| [5] | ZHOU Y Q, LIU J K, ZHAO G W. Leader glowworm swarm optimization algorithm for solving nonlinear equations systems[J]. Przeglad Elektrotechniczny, 2012, 88(1b):101–106. |
| [6] | MUCHERINO A, SEREF O. Monkey search: A novel metaheuristic search for global optimization[C]//Proceedings of the American Institute of Physics Conference Gainesville. USA: American Institute of Physics, 2007: 162-173. |
| [7] | ALATAS B. Chaotic harmony search algorithms[J]. Applied Mathematics and Computation, 2010, 216(9):2687–2699. DOI:10.1016/j.amc.2010.03.114 |
| [8] | YANG X S, DEB S. Cuckoo search via Levy flights[C]//Proceedings of the World Congress on Nature and Biologically Inspired Computing. Coimbatore, India: IEEE, 2009: 210-214. |
| [9] | YANG X S. A new metaheuristic bat-Inspired algorithm[M]//GONZÁLEZ J R, PELTA D A, CRUZ C (eds. ). Nature Inspired Cooperative Strategies for Optimization. Berlin, Germany: Springer-Verlag, 2010: 65-74. |
| [10] | CUEVAS E, CIENFUEGOS M, ZALDÍVAR D, et al. A swarm optimization algorithm inspired in the behavior of the social-spider[J]. Expert Systems with Applications, 2013, 40(16):6374–6384. DOI:10.1016/j.eswa.2013.05.041 |
| [11] | LUBIN T, BILDE T. The evolution of sociality in spiders[J]. Advances in the Study of Behavior, 2007, 37:83–145. DOI:10.1016/S0065-3454(07)37003-4 |
| [12] | UETZ G W, HIEBER C S. Colonial web-building spiders: Balancing the costs and benefits of group living[M]//CHOU J C, CRESPI B J (eds. ). The Evolution of Social Behavior in Insects and Arachnids. Cambridge, England: Cambridge University Press, 1997. |
| [13] | AVILES L. Sex-ratio bias and possible group selection in the social spider Anelosimus eximius[J]. The American Naturalist, 1986, 128(1):1–12. DOI:10.1086/284535 |
| [14] | BURGESS J W, UETZ W G. Social spacing strategies in spiders[M]//WITT P N, ROVNER J S (eds. ). Spider Communication: Mechanisms and Ecological Significance. Princeton, New Jersey: Princeton University Press, 1982. |
| [15] | SALOMON M, SPONARSK C, LAROCQUE A, et al. Social organization of the colonial spider Leucauge sp.in the Neotropics:Vertical stratification within colonies[J]. Journal of Arachnology, 2010, 34(3):46–451. |
| [16] | YIP E C, POWERS K S, AVILS L. Cooperative capture of large prey solves scaling challenge faced by spider societies[J]. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(33):11818–11822. DOI:10.1073/pnas.0710603105 |
| [17] | BOLTE J, DANIILIDIS J A, LEWIS A. The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems[J]. SIAM Journal on Optimization, 2006, 17(4):1205–1223. |
| [18] | RAVIKUMAR K, ANAND S, SYDULU M. A novel multi-agent based PSO approaches for security constrained optimal power flows using smooth and non-smooth cost functions[J]. International Journal of Computer Applications, 2012, 41(3):14–21. DOI:10.5120/5521-7552 |
| [19] | VAISAKH K, SRINIVAS L R. Adaptive PSODV algorithm for OPF with non-smooth cost functions and statistical analysis[J]. Simulation Modelling Practice and Theory, 2011, 19(9):1824–1846. DOI:10.1016/j.simpat.2011.04.013 |
| [20] | SAYAH S, ZEHAR K. Modified differential evolution algorithm for optimal power flow with non-smooth cost functions[J]. Energy Conversion and Management, 2008, 49(11):3036–3042. DOI:10.1016/j.enconman.2008.06.014 |
| [21] | BURGES C J C, RAGNO R, LE Q V. Learning to rank with non-smooth cost functions[C]//Proceedings of the 19th International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2006. |
| [22] | NEYESTANI M, FARSANGI M M, NEZAMABADI-POUR H. A modified particle swarm optimization for economic dispatch with non-smooth cost functions[J]. Engineering Applications of Artificial Intelligence, 2010, 23(7):1121–1126. DOI:10.1016/j.engappai.2010.06.006 |
| [23] | LU S F, SUN C F, LU Z D. An improved quantum-behaved particle swarm optimization method for short-term combined economic emission hydrothermal scheduling[J]. Energy Conversion and Management, 2009, 51(3):561–571. |
| [24] | MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69:46–61. DOI:10.1016/j.advengsoft.2013.12.007 |
 2017, Vol. 24
2017, Vol. 24 


