【研究意义】考虑具有如下形式的非线性方程组:
| $g\left( x \right) = 0,$ | (1) |
其中,$g\left( x \right):{\Re ^n} \to {\Re ^n}$为连续可微函数.问题(1)在工程中有广泛应用,例如函数逼近,非线性拟合等.到目前为止,有多种算法可以用来解决问题(1),例如:Gauss-Newton方法[1-4],信赖域方法[5],拟牛顿法[6]等.其中Gauss-Newton方法要求在算法迭代过程中Jacobian矩阵列满秩,这无疑限制了算法的应用范围.为解决此类问题,Levenberg[4]和Marquardt[1]提出Levenberg-Marquardt方法(L-M方法).令$f\left( x \right) = \frac{1}{2}g\left( x \right){^2}$,假设g(x)有零点,那么非线性方程(1)等价于如下优化问题:
| $\min f\left( x \right),x \in {\Re ^n}.$ |
传统L-M方法通过求解下述模型获取搜索方向
| ${s_k} = \mathop {{\rm{rag }}\min }\limits_{s \in {\Re ^n}} {J_k}s + {g_k}{^2} + {\mu _k}s{^2}.$ | (2) |
搜索方向为
| ${s_k} = (J_k^T{J_k} + {\mu _k}I)1J_k^T{g_k},$ | (3) |
式中,gk∶=g(xk),sk是g(x)在xk处的下降方向,Jk∶=J(xk)是g(x)在xk处的Jacobian矩阵,μk>0为迭代参数.不难看出,传统L-M方法的每一次迭代都需要计算Jacobian矩阵,这对于大规模问题,会增加算法的计算存储量和时间.【前人研究进展】绝对值方程(AVE)是由Rohn[7]首次提出,是一类不可微的NP-hard问题[8].文献[9]证明该方程解的存在性和唯一性.文献[10]也给出一类绝对值方程与线性互补问题的等价关系.在AVE求解方面,Caccetta 等[11]提出用光滑牛顿方法求解绝对值方程,并且证明其具有全局收敛性质.Mangasarian[12]提出用广义牛顿方法求解此类问题.Ketabchi等[13]提出一种范数方法求解绝对值方程.更多绝对值方程的求解方法见参考文献[14-15].【本研究切入点】为有效求解大规模问题,本文在适当的条件下提出一种在不需要非退化假设[16]即可具备全局收敛性,并且在一定条件下具有二次收敛性的算法.最重要的是,可以不必在每次迭代时都计算Jacobian矩阵,而且对于Jacobian矩阵Jk,通过BFGS推广得到.令yk=g(xk+1)-g(xk),Bk为广义BFGS,有近似关系:
| ${y_k} = g({x_{k + 1}}) - g({x_k}) \approx \nabla g({x_{k + 1}}){s_k}.$ | (4) |
此时,Bk+1满足正割方程Bk+1sk=yk,又有逼近关系:
| ${B_{k + 1}}{s_k} \approx \nabla g({x_{k + 1}}){s_k}.$ |
这意味着Bk+1沿方向sk逼近▽g(xk+1),即
| ${B_{k + 1}} = {B_k} - \frac{{{B_k}{s_k}s_k^T{B_k}}}{{s_k^T{B_k}{s_k}}} + \frac{{{y_k}y_k^T}}{{y_k^T{s_k}}},$ | (5) |
其中,${s_k} = {x_{k + 1}} - {x_k},{y_k} = g({x_{k + 1}}) - g({x_k}),{x_{k + 1}}$为下一次迭代.【拟解决的关键问题】提出一种基于BFGS更新的L-M算法,并分析算法在如下形式的绝对值方程中的应用:
| $g\left( x \right): = Ax - \left| x \right| - b = 0,$ | (6) |
其中,A,b为给定的已知常量矩阵或向量,$x,b \in {\Re ^n},A \in {\Re ^{n \times n}},x = {({x_1},{x_2}, \ldots ,{x_n})^T}$.文中,‖‖表示欧几里得范数.
1 绝对值方程的基本结论Mangasarian[8]证明求解AVE是一个不可微的NP-hard的优化问题.又由文献[17-18]可知基于|x|的次梯度的广义Jacobian矩阵$\partial \left| x \right|$为一对角矩阵,即
| $h\left( x \right) = {\rm{duag}}({\rm{sign}}\left( x \right)),$ | (7) |
其中,
| ${\rm{sign}}\left( x \right) = \left\{ \begin{array}{l} 1,{\rm{when}}x > 0,\\ 0,{\rm{when}}x = 0,\\ - 1,{\rm{when}}x < 0. \end{array} \right.$ |
diag(·) 表示一对角阵,即有$\partial $g(x)∶=J(x)=A-h(x).
根据文献[10]中的性质3和4,给出绝对值方程解的存在性和唯一性基本结论.
引理1 i) 若$A \in {\Re ^n} \times {\Re ^n}$,且A的所有奇异值都大于1,则对任意的$b \in {\Re ^n}$,绝对值方程存在唯一解;
ii) 若$A \in {\Re ^n} \times {\Re ^n}$,且‖A-1‖<1,则对任意的b$b \in {\Re ^n}$,绝对值方程存在唯一解.
2 算法及其收敛性分析基于BFGS更新,提出一种BFGS Levenberg-Marquardt算法.
算法1
Step 0 选取参数β,σ∈(0,1),μ0>0,初始迭代点x0∈${\Re ^n}$,0≤ε≤1.令k∶=0.
Step 1 若f(x)≤ε,算法终止;否则,进入Step 2.
Step 2 求解方程组$(J_k^T{J_k} + {\mu _k}I)s = - J_k^T{g_k}$,得到sk.
Step 3 Armijo线搜索.令λk是满足下面不等式的最小非负整数λ:
| $f({x_k} + {\beta ^\lambda }{s_k}) \le {f_k} + \sigma {\beta ^\lambda }\nabla f_k^T{s_k},$ | (8) |
令${\alpha _k}: = {\beta ^{{\lambda _k}}},{x_{k + 1}}: = {x_k} + {\alpha _k}{s_k}.$
Step 4 μk=‖g(xk)‖1+τ,τ∈[0,1],令yk=gk+1-gk,如果yksk>0,按照(5)式更新Jk+1;否则,令Jk+1=Jk.
Step 5 令k:=k+1,转Step 1.
引理 2 式(2)中,sk是f(x)在xk处的下降方向.
证明 由最优性条件,知sk满足
| $\begin{array}{l} \nabla \left( {{J_k}s + {g_k}{^2} + {\mu _k}s{^2}} \right) = 2[(J_k^T{J_k} + \\ {\mu _k}I)s + J_k^T{g_k}] = 0, \end{array}$ |
求得${s_k} = - {(J_k^T{J_k} + {\mu _k}I)^{1}}J_k^T{g_k}$.若$J_k^T{g_k} \ne 0$,则对$\forall \mu k > 0$,有
| $\begin{array}{l} {\left( {J_k^T{g_k}} \right)^T}{s_k} = - {\left( {J_k^T{g_k}} \right)^T}(J_k^T{J_k} + \\ {\mu _k}I{)^{1}}(J_k^T{g_k}) < 0. \end{array}$ |
所以,sk是f(x)在xk处的下降方向,则引理2得证.
定理 1(全局收敛性) 假设{xk}由算法1迭代产生得到,且步长满足Armijo线搜索准则,如果存在一个子序列xkj→x*,而且满足相应的子序列{J(xki)TJ(xki)+μkiI}收敛于正定矩阵J(x*)TJ(x*)+μ*I,那么,▽f(x*)=0.
证明 若▽f(xk)≠0,则sk≠0.由引理2,μk>0及xkj→x*得到
| $J_{{k_j}}^T{J_{{k_j}}} \to J{({x^*})^T}J({x^*}),{u_{{k_j}}} \to {u^*}.$ |
由于skj=-[J(xkj)TJ(xkj)+μkjI]-1J(xkj)Tg(xkj),则skj→s*=-[J(x*)TJ(x*)+μ*I]-1J(x*)Tg(x*).
因此对于β∈(0,1),存在非负整数λ*使得
| $f({x^*} + {\beta ^{{\lambda ^*}}}{s^*}) < f\left( {{x^*}} \right) + \sigma {\rm{ }}{\beta ^{{\lambda ^*}}}\nabla f{({x^*})^T}{s^*}.$ |
对于子列xkj→x*,当j充分大时,有
| $f({x_{{k_j}}} + {\beta ^{{\lambda ^*}}}{s_{{k_j}}}) < f\left( {{x_{{k_j}}}} \right) + \sigma {\rm{ }}{\beta ^{{\lambda ^*}}}\nabla f{\left( {{x_{{k_j}}}} \right)^T}{s_{{k_j}}}.$ |
由Armijo步长准则知λ*≥λkj,所以
| $\begin{array}{l} f\left( {{x_{{k_j} + 1}}} \right) = f\left( {{x_{{k_j}}} + {\beta ^{{\lambda _{{k_j}}}}}{s_{{k_j}}}} \right) \le f\left( {{x_{{k_j}}}} \right) + \\ \sigma {\beta ^{{\lambda _{{k_j}}}}}\nabla f{(_{{k_j}}^x)^T}{s_{{k_j}}} \le f({x_{{k_j}}}) + \sigma {\rm{ }}{\beta ^{{m^*}}}\nabla f{\left( {_{{k_j}}^x} \right)^T}{s_{{k_j}}}, \end{array}$ |
即对充分大的j,有
| $f({x_{{k_{j + 1}}}}) \le f({x_{{k_j}}}) + \sigma {\beta ^{{\lambda ^*}}}\nabla f{\left( {{x_{{k_j}}}} \right)^T}{s_{{k_j}}}$ | (9) |
又
| $\mathop {\lim }\limits_{j \to \infty } f({x_{{k_{j + 1}}}}) = \mathop {\lim }\limits_{j \to \infty } f({x_{{k_j}}}) = f({x^*}),$ |
从而对(9)式两边求极限,得
| $f({x^*}) \le f({x^*}) + \sigma {\beta ^{{\lambda ^*}}}\nabla f{({x^*})^T}{s^*}.$ |
这与引理2矛盾,所以▽f(x*)=0.由反证法知定理1得证.
又根据文[19]中定理7.4和注7.2,可以得到算法的收敛速度是二次的.这里省去二次收敛性质的证明过程,详细证明见文献[19].文献[20]也给出了类似的证明.
定理 2(二次收敛性质) 假设{xk}是由算法迭代得到的,且收敛到f(x)的一个局部最小值点x*,μk=‖g(xk)‖1+τ,τ∈[0,1],那么,算法的收敛速度是二次收敛的.
3 数值实验以求解绝对值方程问题为例,验证算法1对于求解大规模优化问题的有效性.实验的所有代码都在Matlab R2010b中运行,其中,电脑的配置:CPU为Intel Pentium(R) Dual-Core E5800 3.20 GHz,SDRAM为2.00 GB的Windows7操作系统.
在引理1的条件下,对随机生成不同维数的绝对值方程进行计算,维数Dim分别设置为500,1000,1500,2000,2500,3000.对于不同维数的绝对值方程,分别随机生成10次进行计算并记录数据.在每个随机问题的求解中,算法的参数选择为β=0.5,σ=0.3,τ=12,ε=10-8,初始点x0=rand(n,1).
数值实验结果见表 1,其中,Dim表示问题维数;Itertotal表示算法1求解10次问题所需的总迭代次数;Cputimetotal表示算法求解10次问题所需总时间;Optaverage表示算法求解10次问题的平均误差,即
| 表 1 数值结果 Table 1 Numerical results |
| ${\rm{Op}}{{\rm{t}}_{{\rm{average}}}} = \frac{{\sum\limits_{i = 1}^{10} {(f_{{\rm{f}} {\rm{in}} {\rm{al}}}^i - {\rm{ops}})} }}{{10}}.$ |
这里,${f_{{\rm{f}} {\rm{in}} {\rm{al}}}^i}$为算法1求解第i个随机算例的终值,ops为对应问题的最优值,在本文中为0.对于随机生成的不同维数算例中,每种维数选取其中一次做Opt(Iter)值迭代随迭代次数Iter的变化图(图 1).结果显示算法1是有效的.
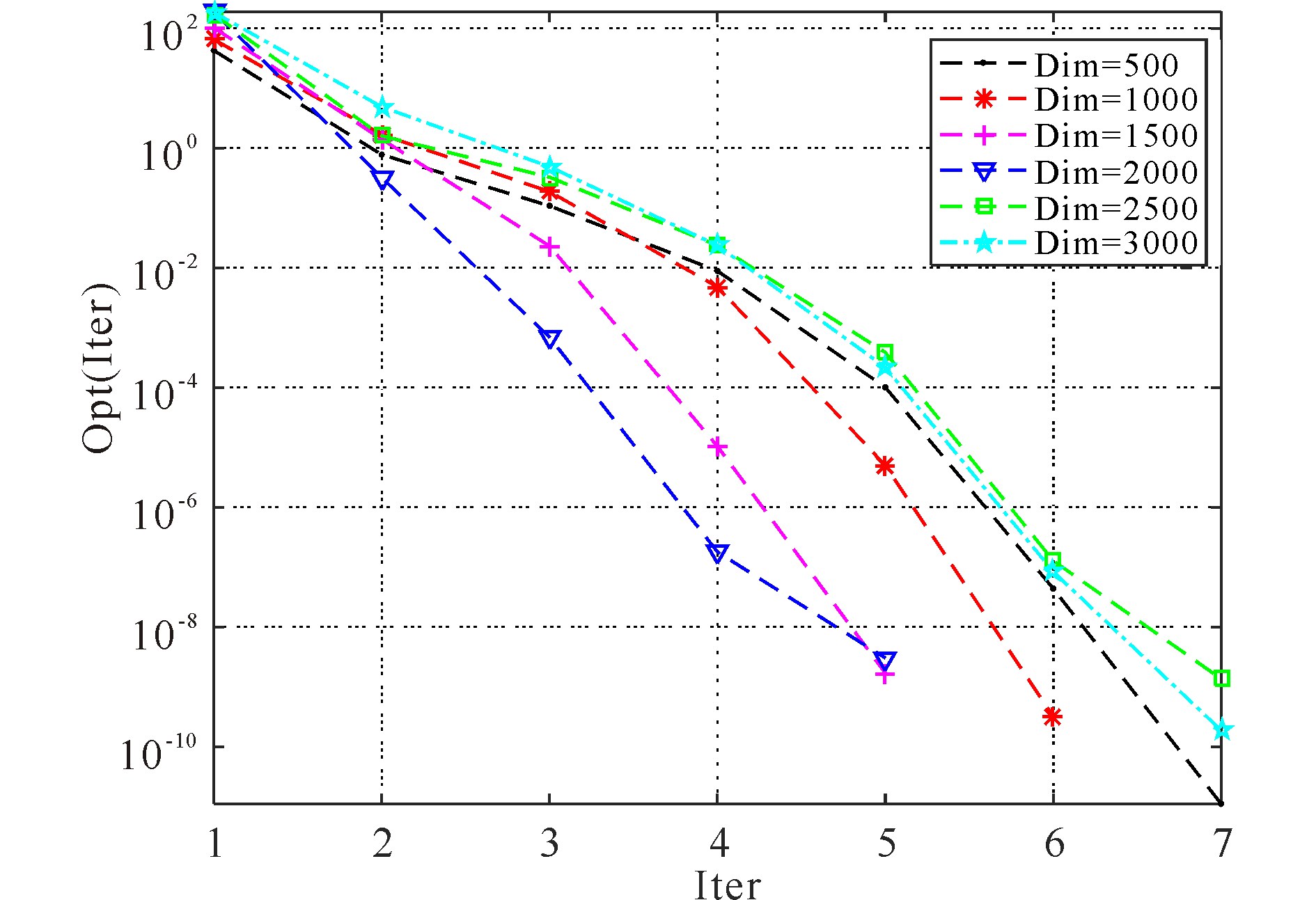
|
图 1 Opt(Iter)的值随迭代次数Iter的变化 Fig.1 The values of Opt(Iter) with the number of iterations Iter |
本文提出一种基于BFGS更新的L-M算法,证明算法具有全局收敛性和二次收敛性质.该算法在每次迭代中,可以避免计算Jacobian矩阵,这在处理大规模问题中可以节约CPU耗费时间.在数值实验中,我们用算法测试了随机生成不同维数绝对值方程问题,结果表明算法是有效的.
| [1] |
MARQUARDT D W. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431. DOI:10.1137/0111030 |
| [2] |
NOCEDAL J, WRIGHT S J. Numerical Optimization[M]. New York: Springer-Verlag, 2006.
|
| [3] |
BERTSEKAS D P. Nonlinear Programming[M]. Belmount,Mass,USA: Athena Scientific, 1999.
|
| [4] |
LEVENBERG K. A method for the solution of certain non-linear problems in least squares[J]. Quarterly of Applied Mathematics, 1944, 2(2): 164. |
| [5] |
YUAN Y X. Trust Region Algorithms for Nonlinear Equations[M]. Hong Kong: Department of Mathematics,Hong Kong Baptist University, 1994.
|
| [6] |
ZHU D T. Nonmonotone backtracking inexact quasi Ne-wton algorithms for solving smooth nonlinear equations[J]. Applied Mathematics and Computation, 2005, 161(3): 875. DOI:10.1016/j.amc.2003.12.074 |
| [7] |
ROHN J. Systems of linear interval equations[J]. Linear Algebra and its Applications, 1989, 126: 39. DOI:10.1016/0024-3795(89)90004-9 |
| [8] |
MANGASARIAN O L. Absolute value programming[J]. Computational Optimization and Applications, 2007, 36(1): 43. DOI:10.1007/s10589-006-0395-5 |
| [9] |
ROHN J. A theorem of the alternatives for the equation[J]. Linear and Multilinear Algebra, 2004, 52(6): 421. DOI:10.1080/0308108042000220686 |
| [10] |
MANGASARIAN O L, MEYER R R. Absolute value equations[J]. Linear Algebra and Its Applications, 2006, 419(2/3): 359. |
| [11] |
CACCETTA L, QU B, ZHOU G L. A globally and qu-adratically convergent method for absolute value equations[J]. Computational Optimization and Applications, 2011, 48(1): 45. DOI:10.1007/s10589-009-9242-9 |
| [12] |
MANGASARIAN O L. A generalized newton method for absolute value equations[J]. Optimization Letters, 2009, 3(1): 101. DOI:10.1007/s11590-008-0094-5 |
| [13] |
KETABCHI S, MOOSAEI H. An efficient method for optimal correcting of absolute value equations by minimal changes in the right hand side[J]. Computers & Mathematics with Applications, 2012, 64(6): 1882. |
| [14] |
YONG Q L. An iterative method for absolute value equations problem[J]. Information, 2013, 16(1): 7. |
| [15] |
HU S L, HUANG Z H. A note on absolute value equations[J]. Optimization Letters, 2010, 4(3): 417. DOI:10.1007/s11590-009-0169-y |
| [16] |
YUAN G L, WEI Z X, LU X W. A BFGS trust-region method for nonlinear equations[J]. Computing, 2011, 92(4): 317. DOI:10.1007/s00607-011-0146-z |
| [17] |
POLYAK B T. Introduction to Optimization[M]. New York: Optimization Software Inc, 1987.
|
| [18] |
ROCKAFELLAR R T.New Applications of Duality in Convex Programming[C]//Proceedings of the Fourth Conference on Probability.Brasov,1971.
|
| [19] |
马昌凤. 最优化方法及其Matlab程序设计[M]. 北京: 科学出版社, 2010. MA C F. Optimization Methods and Matlab Programming[M]. Beijing: Science Press, 2010. |
| [20] |
袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 1997. YUAN Y X, SUN W Y. Optimization Theory and Method[M]. Beijing: Science Press, 1997. |
 2016, Vol. 23
2016, Vol. 23 


