2. 北京理工大学机电学院,北京 100081
2. School of Mechatronical Engineering, Beijing Institute of Technology, Beijing, 100081, China
随着人口老龄化的日益加剧,脑卒中因其高发病率、高死亡率、高致残率、高复发率和多并发症等特点[1],受到社会各界的广泛关注。虽然现代医疗水平已经发展到一个较高的水平,且脑卒中患者的生还率大大提升,但是脑卒中导致的人体机能损伤依旧无法快速治愈,仍需经过一个漫长的步态恢复过程[2],这对患者身心造成巨大伤害,也增加了患者家庭的经济负担[3, 4]。脑卒中患者的脑细胞在病发后两到三周内会出现凋亡和坏死,这是神经细胞的主要死亡方式[5]。因此,脑卒中治疗的关键在于重建神经元之间的联络[6]。通过康复训练帮助患者进行步态训练,可以防止患者肌肉萎缩,有利于神经系统的重建,增强对患肢的控制力[7]。康复过程对医师的体力损耗巨大,且康复医师数量严重不足[8, 9]。有证据表明,康复机器人的应用对于患者的康复可以起到一定的作用[10],同时可以减轻医师的身体负担和患者的经济负担。
体重支持(BWS)系统是下肢康复机器人最重要的部分。BWS系统可为患者提供保护,避免患者跌倒造成二次伤害[11],同时可以减轻患者腿部负担,减小体力消耗,增加训练时长,提高训练效率[12]。目前市面上常见BWS系统的主要结构包括固定框、钢索、滑轮和伺服电机等[13]。BWS系统发展迅速,已经由固定式系统发展为可移动式系统[14],使得康复训练更加便捷。Gordon等[15]提出一种基于力闭环的悬臂减重支撑系统控制方法,主要利用电机带动绳索,根据设定减重值对康复支持力进行调节。这种控制算法响应速度快,误差小,但对于动力学模型较复杂的系统,其控制效果差,局限性较强。Ma等[16]提出一种基于加速度的控制策略,根据患者训练时的加速度对康复支持力进行调节,可以有效降低惯性,稳定性较好。但对于加速度的采集比较困难,控制效果受数据准确性影响很大。上述BWS系统的恒力控制方案存在一定的控制优势,但也存在依赖系统模型、数据采集困难以及无法适用患者的整个康复过程等问题。
针对上述问题,本研究提出一种基于导纳模型的双闭环变参数导纳控制算法,拟解决下肢康复机器人BWS系统康复支持力不够稳定及康复训练适用性不强等问题,从而提高使用下肢康复机器人进行康复训练时的训练效果,满足不同患者在不同康复阶段的训练需求。
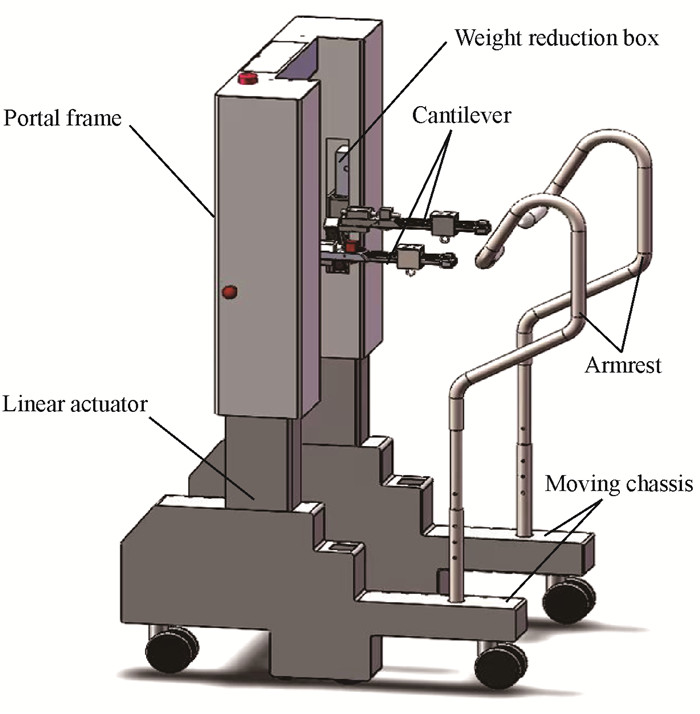
1 体重支持系统分析 1.1 机械结构分析下肢康复机器人的机械结构如图 1所示,主要由移动底盘、龙门架、电动推杆、扶手、减重盒和悬臂组成。移动底盘使用2个轮毂电机作为主动轮,4个万向轮作为从动轮,可以满足下肢康复机器人在行走康复训练中跟随患者移动的康复训练需求;龙门架是下肢康复机器人的主体框架,所有功能模块均安装于其上并实现各自功能;减重盒和电动推杆是BWS系统的主要功能结构,通过减重盒内部的弹簧拉伸提供支持力,并由内部拉力传感器采集弹簧的拉力值,实现对下肢康复机器人所提供支持力的监测;与减重盒配合使用的电动推杆主要有两个功能:一是根据患者需求调节支持力大小,二是将患者从轮椅拉起到站立状态并根据患者身高调节悬臂高度;穿戴减重服的患者悬吊于悬臂之上,患者两肩之间前后距离差由安装在悬臂上的位移传感器进行实时采集,通过对位移传感器的数据进行处理,判断患者的运动意图,从而控制轮毂电机带动整个下肢康复机器人跟随患者移动;前端扶手供患者抓握,用于辅助患者保持身体平衡,限制患者重心在水平方向的移动,防止跌倒,提高患者训练时的安全感。
|
| 图 1 下肢康复机器人机械结构 Fig.1 Mechanical structure of lower limb rehabilitation robot |
1.2 控制方案分析
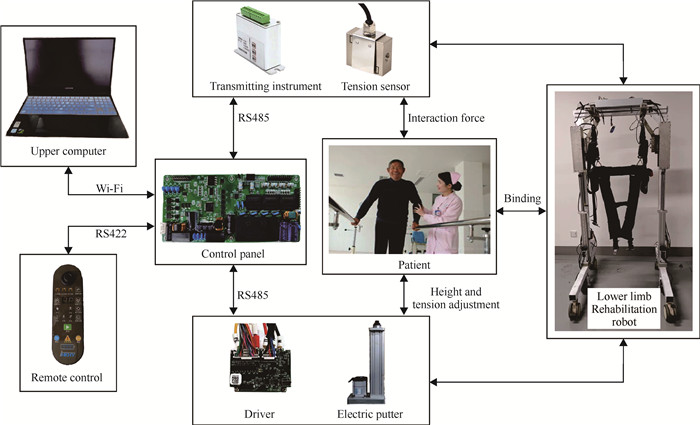
BWS系统硬件框架如图 2所示。下肢康复机器人的控制方式主要有遥控器控制和上位机控制,通过向控制板发送控制指令,再由控制板控制对应驱动器,实现对整个系统的控制。不同身高患者的需求可以通过控制电动推杆上下移动来满足,同时,控制板还可以控制电动推杆的移动进而控制弹簧伸缩量,从而调节到适宜的减重值。BWS系统对患者的支持力通过绑带中间的拉力传感器实时采集,并通过变送器将数据传输至控制板,控制板通过Wi-Fi将数据传输至上位机进行数据处理,并可根据处理结果反向发送指令,实现对BWS系统的调节。下肢康复机器人的功能模式主要有遥控器模式、上位机模式和自由模式3种。在遥控器模式和上位机模式下,需要医护人员控制机器人移动,可以根据制定的训练轨迹进行行走训练。自由模式下患者可以根据自己的想法随意走动,下肢康复机器人跟随患者行走,具有更高的自由度,可以充分调动患者的训练积极性[17]。BWS系统作为下肢康复机器人的主要功能模块,在康复训练中起着重要作用,其中电动推杆电机的控制精度和拉力传感器的测量精度都对支持力的控制起着决定性的作用。此外,系统数据的读取和处理速度也至关重要。
|
| 图 2 BWS系统硬件框架图 Fig.2 Hardware frame diagram of BWS system |
2 系统分析与控制器设计 2.1 导纳控制模型
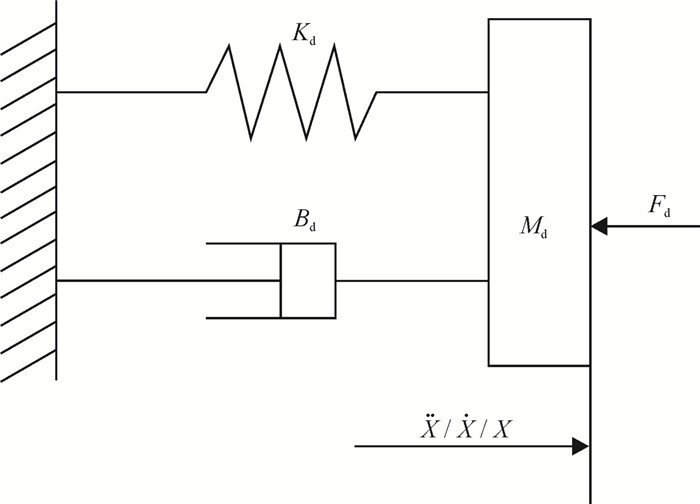
常用的人机交互控制方法主要有刚度控制、阻抗控制和导纳控制等,可以单独使用也可以混合使用[18]。其中导纳控制将被控对象和环境看作统一的整体,将机器人与环境的接触过程等效为“质量-弹簧-阻尼”模型,如图 3所示,其中,Md为质量块的质量;Bd为阻尼器的阻尼;Kd为弹簧的刚度;X、Ẋ、Ẍ分别为质量块的位置、速度和加速度;Fd为外界环境作用力。
|
| 图 3 等效“质量-弹簧-阻尼”模型 Fig.3 Equivalent "mass-spring-damping" model |
通过对模型中的质量块进行受力分析,建立质量-弹簧-阻尼系统的二阶微分方程如下:
| $\;\;\;\; F_{\mathrm{d}}=M_{\mathrm{d}} \ddot{X}+B_{\mathrm{d}} \dot{X}+K_{\mathrm{d}} X \text { 。} $ | (1) |
当系统受到的外界环境作用力增加Fe时,若想保持系统状态不变,则此时:
| $ \begin{aligned} & \quad F_{\mathrm{d}}+F_{\mathrm{e}}=\left(M_{\mathrm{d}}+M_{\mathrm{e}}\right) \ddot{X}+\left(B_{\mathrm{d}}+B_{\mathrm{e}}\right) \dot{X}+ \\ & \left(K_{\mathrm{d}}+K_{\mathrm{e}}\right) X, \end{aligned} $ | (2) |
其中,Me, Be, Ke分别为期望惯性、期望阻尼和期望刚度。
公式(2)与公式(1)两式相减,可得:
| $\;\;\;\; F_{\mathrm{e}}=M_{\mathrm{e}} \ddot{X}+B_{\mathrm{e}} \dot{X}+K_{\mathrm{e}} X \text { 。} $ | (3) |
由此可知,当机器人受到外力作用时,可以通过调节惯性、阻尼、刚度参数来平衡外界扰动力,保持系统所受合力不变。
2.2 支持系统恒力控制设计在整个BWS系统中,存在以下平衡关系:
| $\;\;\;\; \left\{\begin{array}{l} F_{\mathrm{ref}}=F_1+F_2 \\ F_1=k x_1 \\ F_2=k x_2 \end{array}, \right. $ | (4) |
其中,Fref为康复支持力,F1、F2分别为减重盒内左、右两弹簧所提供的拉力,k为弹簧的弹性系数,x1、x2分别为左、右两减重盒内弹簧的伸长量。
康复支持力是为了减轻患者双脚的负担和运动时的惯性力,康复训练时,人体重心的动力学公式如下:
| $\;\;\;\; F_{\mathrm{leg}}=m \ddot{x}_{\mathrm{p}}+m g, $ | (5) |
其中,Fleg为患者腿部的支撑力,m是患者的重量,Ẍp是患者重心在竖直方向上的加速度,g为重力加速度。
下肢康复机器人对患者的支持力可分为两部分:
| $ F_{\mathrm{w}}=m_{\mathrm{w}} g, $ | (6) |
| $ F_{\mathrm{i}}=m_{\mathrm{i}} a, $ | (7) |
其中,Fw为重力补偿, mw为重量补偿, Fi为惯性力补偿, mi为减少的重量,a为惯性力在竖直方向上引起的加速度。
将Fw、Fi作用于人体,则人体受力变化为
| $ F_{\mathrm{leg}}+F_{\mathrm{w}}+F_{\mathrm{i}}=m \ddot{x}_{\mathrm{p}}+m g \text { 。} $ | (8) |
将公式(6)、(7)带入公式(8)并整理后可得:
| $ F_{\mathrm{leg}}=\left(m-m_{\mathrm{i}}\right) \ddot{x}_{\mathrm{p}}+\left(m-m_{\mathrm{w}}\right) g \text { 。} $ | (9) |
对比公式(5)可以看出,公式(9)中患者下肢所需的力有所减小,可减轻患者的腿部负担。
利用导纳控制可以实现康复支持力的动态控制,设计的康复支持力如下:
| $ F_{\mathrm{ref}}=m_{\mathrm{i}} \ddot{x}_{\mathrm{p}}+b \dot{x}_{\mathrm{p}}+k x_{\mathrm{p}}+m_{\mathrm{w}} g, $ | (10) |
其中,Ẋp、xp分别为患者重心在竖直方向上的速度和位移。
2.3 双闭环控制器在整个康复周期中,患者的下肢力量不断增强,行走速度也逐渐变快,对于体重支持系统的响应性能需求不同,因此控制算法参数也应随其改变,以保证康复支持力的准确性和稳定性。患者各康复阶段最明显的区别在于患者的行走速度,可将其作为康复阶段的判别依据。建立系统中力与患者移动速度(v)的关系,则公式可写为
| $ F_{\mathrm{e}}=M_{\mathrm{e}} \dot{v}+B_{\mathrm{e}} v+K_{\mathrm{e}} \int v \mathrm{~d} t, $ | (11) |
其中,
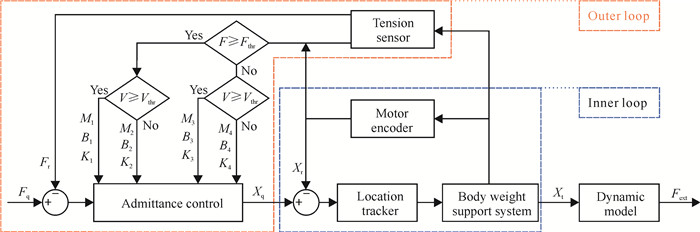
康复前期患者平衡能力较差,行走较慢,所需康复支持力较大,惯性参数、阻尼参数和质量参数均应适当变大,以提高系统稳定性。康复后期行走较快,所需康复支持力相对较小,惯性参数、阻尼参数和质量参数可以适当减小,以提高系统响应速度。为此,设计一种双闭环变参数导纳控制器,外环为力环,根据力误差可以快速做出反应;内环为位移环,通过电机转动提供位移补偿,提高控制精度,控制器框架图如图 4所示,其中,Xt为弹簧长度变化量,Fext为BWS系统的输出力,Fthr为拉力阈值,Vthr为速度阈值,M1、B1、K1,M2、B2、K2,M3、B3、K3,M4、B4、K4分别为不同康复情况下的惯性、阻尼、刚度参数。
|
| 图 4 双闭环变参数导纳控制器框架图 Fig.4 Framework diagram of double closed-loop variable parameter admittance controller |
在控制外环中,实际康复支持力(Fr)与期望康复支持力(Fq)的差值作为导纳控制器的输入量,输出中间指令信号——期望位移量(Xq),并将Xq作为内环的输入值。在控制内环中,Xq与实际位移量(Xr)叠加生成新的运动轨迹,并利用比例-积分-微分(PID)控制算法对此轨迹进行跟踪,使其满足系统运行需求。电动推杆作为位移跟踪的实现元件,通过上下移动来拉伸弹簧,进而实现对康复支持力的精确调整。同时,电机驱动响应速度快,控制精度高,成本低[19]。患者的康复训练情景大致分为以下4种:康复支持力大但行动缓慢;康复支持力小但运动速度快;康复支持力大且运动速度快;康复支持力小且行动缓慢。其中,最常见的是前两种情况,分别出现在康复前期和康复后期的训练过程中。在康复训练过程中,下肢康复机器人与患者间存在相互作用力(即人机交互力),可以被拉力传感器实时监测。此外,电机运行速度也可以利用电机编码器实时采集。通过人机交互力以及电机运行速度来判断患者的康复训练情况,自动调整导纳控制器的控制参数,从而保证下肢康复机器人对患者所提供康复支持力的持续和稳定,即实现体重支持系统的恒力控制。
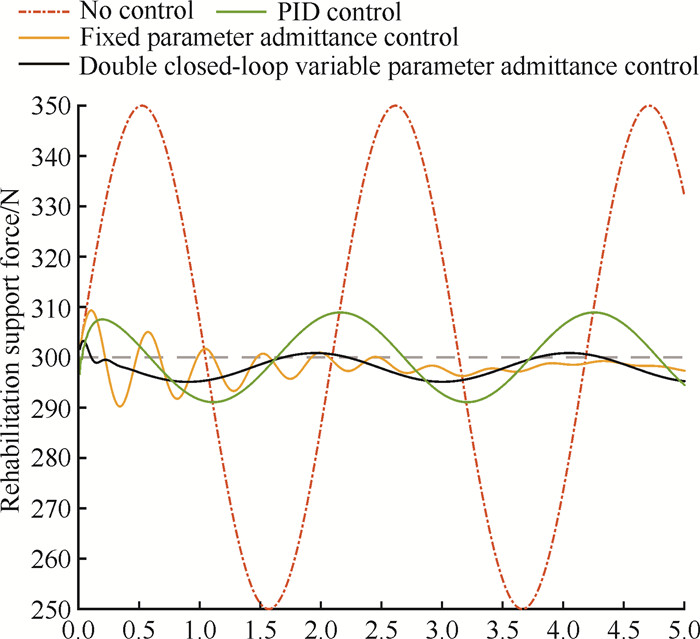
3 仿真分析与实验验证 3.1 MATLAB仿真实验根据患者康复训练时的重心浮动距离值与BWS系统所使用的弹簧弹性系数计算可知,训练过程中康复支持力变化曲线波峰与波谷差值约100 N。康复前期患者下肢力量不足,对患者预设的期望康复支持力为300 N。在患者行走过程中,患者重心呈周期性起伏变化[20],故在无算法控制时,下肢康复机器人与患者间的作用力曲线选取sin函数[F=300+50sin(t)]拟合。相较于无算法控制、固定参数导纳控制和PID控制,双闭环变参数导纳控制精度更高,康复支持力更加稳定,康复支持力误差维持在5 N以内(图 5)。
|
| 图 5 康复前期康复支持力变化仿真 Fig.5 Simulation of changes in rehabilitation support force during the pre-rehabilitation stage |
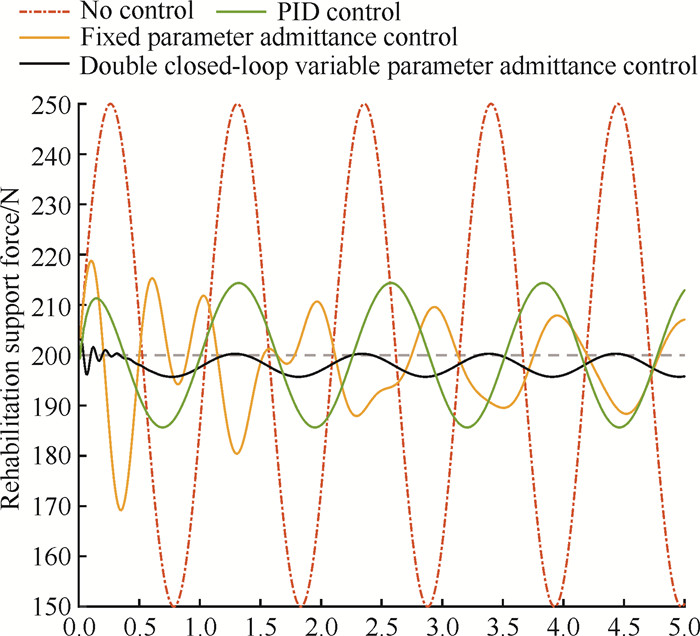
康复后期患者下肢力量有所恢复,行走速度变快,对患者的预设康复支持力为200 N,下肢康复机器人与患者间的作用力曲线取F=200+50sin(2t)。如图 6所示,固定参数导纳控制的康复支持力波动约20 N左右,略优于PID控制效果,但仍不稳定。双闭环变参数导纳控制的康复支持力波动仅5 N左右,波动范围更小,康复支持力稳定性显著提升。
|
| 图 6 康复后期康复支持力仿真 Fig.6 Simulation of changes in rehabilitation support force during the post-rehabilitation stage |
进一步对康复支持力仿真结果进行分析,得到如表 1所示的各控制算法的误差情况。相对于其他两种控制算法,在康复前期、后期中,双闭环变参数导纳控制的最大误差和平均误差都最小,说明其可有效减小患者运动引起的康复支持力波动,保证康复支持力的稳定性及准确性。改变控制器参数可适用于患者的整个康复训练过程,同时也保证了患者的康复训练安全。
| 控制算法 Control algorithm |
康复前期 Pre-rehabilitation stage |
康复后期 Post-rehabilitation stage |
||
| 平均误差 Average errors |
最大误差 Maximum errors |
平均误差 Average errors |
最大误差 Maximum errors |
|
| PID | 9.0 | 14.3 | 5.6 | 8.9 |
| Fixed parameter | 6.9 | 18.8 | 2.4 | 10.2 |
| Variable parameter | 2.0 | 5.7 | 2.4 | 4.9 |
考虑到在对下肢康复机器人不熟悉的情况下,患者康复训练时可能会跌倒,进一步对患者跌倒及康复机器人悬臂位移进行仿真分析(图 7)。患者跌倒时,一方面悬臂跟随患者重心移动,产生缓冲距离并避免与患者对抗;另一方面,悬臂移动到一定位置后,会触发警报并停止移动,防止患者跌落地面造成二次伤害,并向相关人员发出警报信息,以便快速处理患者情况。

|
| 图 7 康复过程跌倒仿真 Fig.7 Fall simulation during the rehabilitation process |
3.2 康复减重行走实验
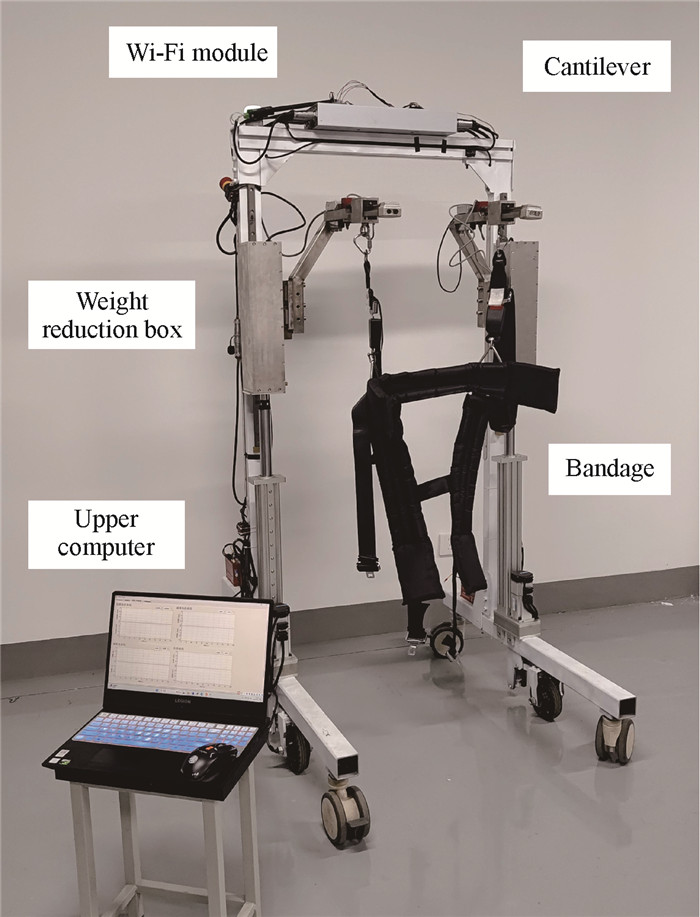
下肢康复机器人可减轻患者腿部负担并辅助患者进行行走训练。康复减重行走实验平台搭建如图 8所示,BWS系统对患者提供的支持力数据经变送器传输到控制板,控制板与上位机之间通过Wi-Fi进行数据传输,每隔一定时间记录1次值。患者穿戴好绑带后,设置合适支持力后发给体重支持系统,切换至自由模式即可进行自主训练。训练过程中,上位机实时接收下肢康复机器人反馈的数据,并自动绘制数据变化曲线。对于所设计的控制算法,为验证其控制效果,采用离线实验的方式进行验证。康复训练结束后,对采集到的数据进行筛选,截取行走过程中的实验数据。由于采集到的数据为一些离散的数据点,因此利用MATLAB软件对离散数据点进行傅里叶函数拟合,从而得到支持力变化曲线。将拟合后的康复支持力变化曲线作为控制器输入并导入算法进行处理得到最终实验结果。
|
| 图 8 下肢康复机器人导纳控制实验平台 Fig.8 Experimental platform for admittance control of lower limb rehabilitation robot |
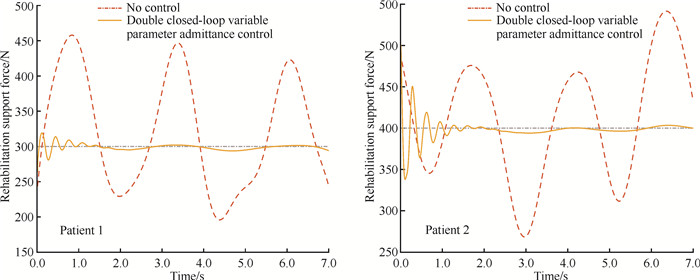
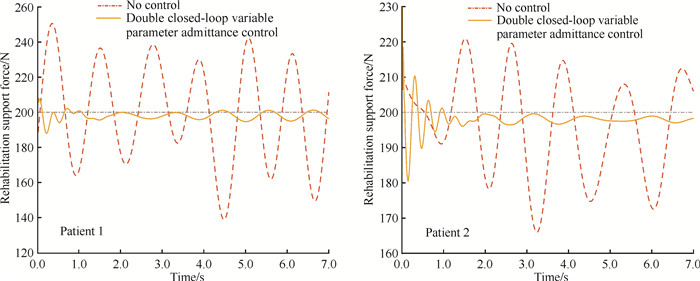
在进行康复训练时,下肢康复机器人所提供的康复支持力应达到患者体重的30%[17]。中国老年人的平均步速为0.54-0.98 m/s[21],步频为40-90步/分钟,患者的步速为正常人的1/3-1/2,步频为15-45步/分钟。实验共两名患者参与,设计实验条件如下:患者1,身高1.8 m,体重75 kg,康复前期和康复后期预设康复支持力分别为300 N和200 N;患者2,身高1.7 m,体重85 kg,康复前期和康复后期预设康复支持力分别为400 N和200 N。两名实验对象康复前期实验结果如图 9所示,康复前期患者行动缓慢,在没有算法控制的情况下,康复支持力波动频率较低,但康复支持力大小变化明显,最大康复支持力误差均超过100 N,平均误差超过50 N。运用双闭环变参数导纳控制算法时,控制器经快速反馈调节后,康复支持力基本保持稳定,平均误差均不超过10 N。在康复后期(图 10),没有算法控制时,康复支持力波动频率较高,康复支持力平均波动约80 N。在双闭环变参数导纳控制算法的加持下,康复支持力波动幅度相较于没有算法控制减小约90%,取得良好控制效果。实验结果表明,所设计的基于双闭环变参数导纳控制的控制器可以有效地改善康复支持力波动大的问题,为患者提供稳定的支持力。
|
| 图 9 康复前期康复支持力实验结果 Fig.9 Experimental results of changes in rehabilitation support force during the pre-rehabilitation stage |
|
| 图 10 康复后期康复支持力实验结果 Fig.10 Experimental results of changes in rehabilitation support force during the post-rehabilitation stage |
4 结论
本文提出了一种双闭环变参数导纳控制算法,根据患者在进行康复训练时行动的快慢自动识别出其所处的康复阶段,并自动调整为合适的参数值,使得下肢康复机器人对患者提供的康复支持力保持相对恒定,康复支持力平均误差保持在10 N以内,相较于无算法控制的情况,康复支持力平均误差减小约90%,控制效果表现较好。此外,该算法还可在患者发生跌倒等突发情况时顺应患者对下肢康复机器人的作用力,避免其对患者产生二次伤害。综上,双闭环变参数导纳控制算法可以提高下肢康复机器人的安全性与舒适性,减轻康复医生的负担,进一步提高患者的康复训练积极性,可为国家医疗设备的发展与进步提供一定的技术参考。
| [1] |
梁妍, 谭寅虎, 邢慧敏, 等. 脑卒中病人过渡期护理研究进展[J]. 循证护理, 2024, 10(5): 845-849. |
| [2] |
MIKOLAJCZYK T, CIOBANU I, BADEA D I, et al. Advanced technology for gait rehabilitation: an overview[J]. Advances in Mechanical Engineering, 2018, 10(7): 168781401878362. |
| [3] |
LIU H, YIN H, YI Y, et al. Effects of different rehabilitation training on balance function in stroke patients: a systematic review and network meta-analysis[J]. Archives of Medical Science: AMS, 2023, 19(6): 1671-1683. |
| [4] |
李林章, 孙妍, 秦华, 等. 脑卒中后患者恐动症的研究进展[J]. 军事护理, 2024, 41(5): 43-46. |
| [5] |
ZHANG Y, KHAN S, LIU Y, et al. Modes of brain cell death following intracerebral hemorrhage[J]. Frontiers in Cellular Neuroscience, 2022, 16: 799753. DOI:10.3389/fncel.2022.799753 |
| [6] |
YAO Z M, SUN X R, HUANG J, et al. Astrocyte-neuronal communication and its role in stroke[J]. Neurochemical Research, 2023, 48(10): 2996-3006. DOI:10.1007/s11064-023-03966-0 |
| [7] |
ZHAO H, YANG J, YANG J, et al. Evaluation of the improvement of walking ability in patients with spinal cord injury using lower limb rehabilitation robots based on data science[J]. Translational Neuroscience, 2023, 14(1): 20220320. DOI:10.1515/tnsci-2022-0320 |
| [8] |
付志鹏. 康复中心脑卒中患者下肢康复产品的人性化设计研究[D]. 长春: 长春工业大学, 2021.
|
| [9] |
VAN DELLEN F, LABRUVÈRE R. Settings matter: a scoping review on parameters in robot-assisted gait therapy identifies the importance of reporting standards[J]. Journal of Neuroengineering and Rehabilitation, 2022, 19(1): 40. DOI:10.1186/s12984-022-01017-3 |
| [10] |
CAMPAGNINI S, LIUZZI P, MANNINI A, et al. Effects of control strategies on gait in robot-assisted post-stroke lower limb rehabilitation: a systematic review[J]. Journal of Neuroengineering and Rehabilitation, 2022, 19(1): 52. DOI:10.1186/s12984-022-01031-5 |
| [11] |
KIM J, OH S, KIM J, et al. A two-wire body weight support system for interactive treadmill [C]//2019 IEEE 16th International Conference on Rehabilitation Robotics (ICORR). Piscataway, NJ, USA: IEEE, 2019: 349-354.
|
| [12] |
LIU B, LI S, LIANG B, et al. Exploring the effects of body weight support systems on lower limb kinematics and muscle characteristics[J]. Biomedical Signal Processing and Control, 2023, 85: 104947. DOI:10.1016/j.bspc.2023.104947 |
| [13] |
FREY M, COLOMBO G, VAGLIO M, et al. A novel mechatronic body weight support system[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2006, 14(3): 311-321. DOI:10.1109/TNSRE.2006.881556 |
| [14] |
PENNYCOTT A, VALLERY H. Body weight support devices for overground gait and balance training [M]//REINKENSMEYER DJ, MARCHAL-CRESPO L, DIETZ V. Neurorehabilitation Technology. Cham: Springer, 2022: 745-756.
|
| [15] |
GORDON K, SVENDESEN B, HARKEMA S J, et al. Closed-loop force controlled body weight support system: US7381163 [P]. 2008-06-03.
|
| [16] |
MA O, DIAO X, MARTINEZ L, et al. Dynamically removing partial body mass using acceleration feedback for neural training [C]//2007 IEEE 10th International Conference on Rehabilitation Robotics. Piscataway, NJ, USA: IEEE, 2007: 1102-1107.
|
| [17] |
ETTEMA S, PENNINK G H, BUURKE T J W, et al. Clinical indications and protocol considerations for selecting initial body weight support levels in gait rehabilitation: a systematic review[J]. Journal of Neuroengineering and Rehabilitation, 2024, 21(1): 97. DOI:10.1186/s12984-024-01389-8 |
| [18] |
赵冬冬, 郭帅, 刘剑翔, 等. 基于变参数导纳控制的康复助行机器人减重支撑系统研究[J]. 工业控制计算机, 2020, 33(12): 83-86. DOI:10.3969/j.issn.1001-182X.2020.12.033 |
| [19] |
周德威. 减重助行机器人结构及控制系统设计[D]. 淮南: 安徽理工大学, 2022.
|
| [20] |
田园. 基于穿戴式IMU的行人定位技术研究[D]. 成都: 电子科技大学, 2021.
|
| [21] |
叶静, 吴紫莺, 王伊伦, 等. 中国老年人步速现状及慢步速的影响因素研究[J]. 中国卫生统计, 2022, 39(4): 494-498. |



