2. 中科星图金能(南京)科技有限公司,江苏南京 211100
2. Zhongke Xingtu Jinneng (Nanjing) Technology Co., Ltd., Nanjing, Jiangsu, 211100, China
随着中国数字经济的持续增长以及《数字中国建设整体布局规划》[1]、《数字农业农村发展规划(2019-2025年)》[2]等相关政策的部署与落地,加快我国水产养殖业的数字化、智慧化进程对我国水产养殖提质增效、产业升级有着重要意义。
在智慧渔场的日常管理中,监控视频作为一种实时性强、场景还原度高的信息媒介,具有极强的使用价值[3]。传统的视频监控需要在屏幕前观看多个镜头画面,零散的监控视频难以与其实际地理位置匹配,并且由于单镜头视域较小,无法满足人们对于宽视域、全场景的要求。在基于数字孪生的智慧渔场中,将视频拼接技术与三维场景进行地理空间化匹配融合[4, 5],可以在成本较低的情况下,得到覆盖范围更广的全景图像,从而减少监控死角,实现监控视频的增点扩面。
目前,国内外针对静态图像拼接技术[6]的研究已经比较成熟。Brown等[7]提出图像拼接算法AutoSitich,其利用SIFT(Scale Invariant Feature Transform)算法进行特征检测、匹配,并使用RANSAC (Random Sample Consensus)算法[8]筛选匹配的特征点对,通过计算全局单应矩阵完成透视变换,再经过图像融合形成全景图,但是AutoSitich算法要求图像的投影中心相同、拍摄图像需要处于同一平面等,这些限制条件在现实中难以被满足;Zaragoza等[9]提出APAP(As-Projective-As-Possible)算法,APAP算法将图像划分为密集网格,每个网格使用一个单应矩阵对齐,减少了图像的畸变程度;Lin等[10]提出AANAP(Adaptive As-Natural-As-Possible)算法,AANAP算法在密集网格的基础上,增加了单应线性优化,提高了拼接结果的观感自然度;江智等[11]在SURF (Speeded Up Robust Features)特征提取算法的基础上,集合图像分块思想,提出IB-SURF图像配准算法,提高了有效特征点占比和特征点质量。
图像拼接是视频拼接中的关键技术,随着图像拼接研究日益成熟,同时对监控画面、无人机拍摄视频的宽视域需求逐渐增加,越来越多研究者开始对视频拼接进行研究。Ling等[12]基于图像拼接的技术,采用加权融合算法进行图像融合,在平台上搭建了几何变换和视频融合的硬件电路,从而实现实时视频融合;Wang等[13]针对机场飞行区视频监控图像中高清图片拼接耗时长和图像拼接重影严重的问题,提出一种改进的超高清全景视频拼接方法,该方法采用改进的Harris角点方法,并使用欧式距离进行特征点匹配,基本满足了视频实时性的需求;张望成等[14]针对局部自适应变形拼接方法中拼接效率低下的问题,引入Deep-DP稠密投影模型估计器来对匹配对进行筛选,同时针对局部形变场建模,提出可适用于GPU计算的平滑形变场计算框架,极大地提高了图像拼接的速度;崔志远[15]在检测匹配点的基础上,增加直线段匹配,通过基于薄板样条估计网格的最终形变位置,提高了图形在拼接形变中直线段的保持能力;武忆涵[16]改进拼接缝算法,在重叠区域保存多条拼接缝,通过背景帧差来判断接缝生成的掩码图,从而实现自适应视频拼接的效果。
为了提高视频图像拼接过程中的特征点提取速度和特征点对匹配精度,同时解决由于视差、光线等环境因素所导致的拼接缝和图像重影问题,本文在基于BRISK(Binary Robust Invariant Scalable Keypoints)+网格运动统计(Grid Motion Statistics, GMS)-RANSAC图像配准算法的基础上,提出结合最佳缝合线和改进渐入渐出融合算法的图像融合算法,优化算法中的能量函数和权值函数。
1 图像拼接算法 1.1 基于BRISK-GMS的图像匹配算法 1.1.1 特征提取算法BRISK在视频图像拼接过程中,确保拼接过程的低延迟和高响应速度至关重要,但是生成高维度的特征描述子所消耗的时长不能满足实时性的需求。为了满足实时性和特征描述的高细节度,本文采取BRISK算法进行特征提取。
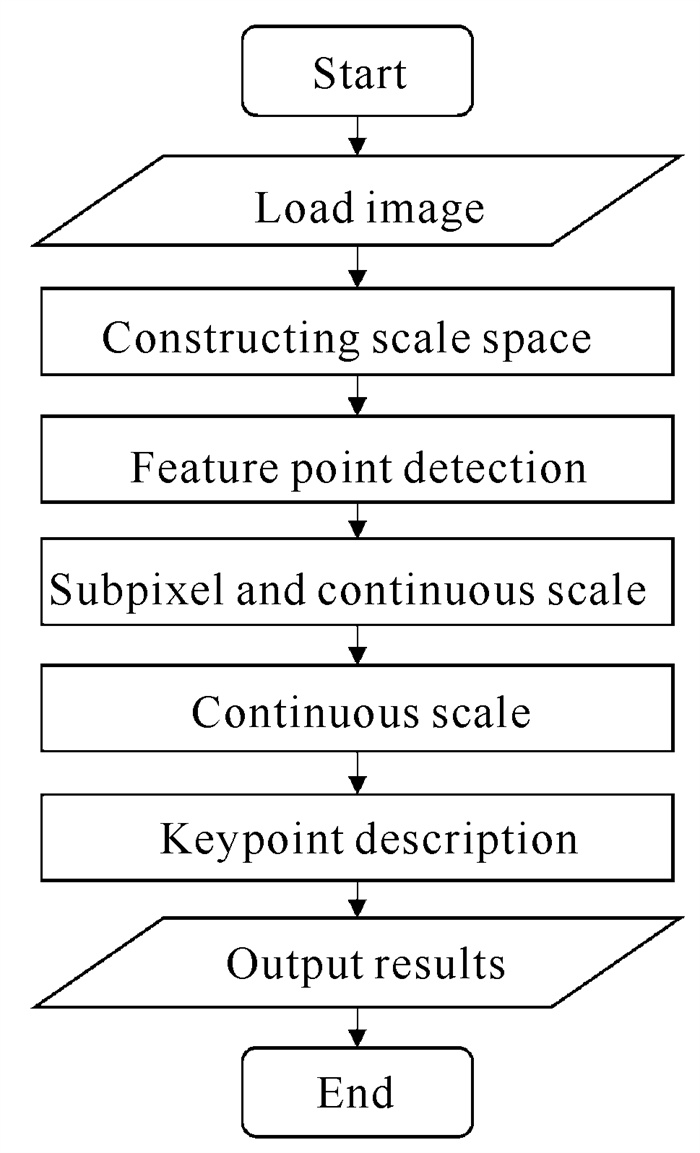
BRISK算法[17]是一种改进的BRIEF (Binary Robust Independent Elementary Features)算法,通过采用FAST(Features from Accelerated Segment Test)算法和二值特征描述子来保证其特征点提取的快速性和所生成描述子的高效性。算法流程如图 1所示。
|
| 图 1 BRISK算法流程 Fig.1 BRISK algorithm process |
BRISK算法的具体流程如下。
① 构造尺度空间并进行关键点检测
BRISK算法构造了n个octave层和n个intra-octave层来组成其尺度空间金字塔(n值一般为4),保证了关键点提取的尺度不变性。octave层和intra-octave层之间的关系为
| $ t\left(c_i\right)=2^i, t\left(d_i\right)=2^i \times 1.5, $ | (1) |
其中ci为第i层octave层,di为第i层intra-octave层。
尺度空间构造完成后,首先对空间中图像使用FAST9-16和FAST5-8[18, 19]算法进行关键点提取,得到粗略的关键点; 然后对关键点的得分值在相邻的两个尺度空间上进行非极大值抑制(其中得分值为角点响应值); 最后,再使用最小二乘法结合得分值拟合得到关键点的亚像素坐标以及对应的尺度。
② 特征点描述
BRISK算法在以尺度空间中每个关键点为中心的多个不同半径的圆环中,均匀选择采样点。每两个采样点为一个采样点对,用Ω表示。短距离采样点对集和长距离采样点对集分别使用S和P表示,其函数表达式为
| $ S=\left\{\left(p_i, p_j\right) \in \varOmega \mid\left\|p_i-p_j\right\|<\delta_{\max }\right\} \subseteq \varOmega, $ | (2) |
| $ P=\left\{\left(p_i, p_j\right) \in \varOmega \mid\left\|p_i-p_j\right\|>\delta_{\min }\right\} \subseteq \varOmega, $ | (3) |
式中,δmax=9.57t,δmin=13.67 t,t为当前特征点所在尺度空间的尺度。同时为了保证所提取的特征点具有旋转不变性,需要通过梯度来计算出特征点的主方向α,梯度表达式和特征点主方向计算表达式如下所示:
| $ g=\left[\begin{array}{l} g_x \\ g_y \end{array}\right]=\frac{1}{L} \sum\limits_{\left(p_i, p_j\right) \in P} g\left(p_i, p_j\right), $ | (4) |
| $ \alpha=\arctan \left(g_x, g_y\right), $ | (5) |
式中,g(pi, pj)为点(pi, pj)的梯度值。在计算特征点描述符之前,需要将采样模板旋转α°,之后计算特征点的描述符,计算表达式为
| $ \begin{aligned} & f(x)= \\ & \left\{\begin{array}{ll} 1, & I\left(p_j^\alpha, \sigma_j\right)>I\left(p_i^\alpha, \sigma_i\right) \\ 0, & \text { other } \end{array} \quad \forall\left(p_i^\alpha, p_j^\alpha\right) \in S, \right. \end{aligned} $ | (6) |
式中,piα为旋转α°后的采样点。
1.1.2 基于GMS-RANSAC算法的特征匹配特征匹配即将两幅图像中提取到的特征点依据其描述子找出相应特征点的对应关系,并在匹配过后删除误匹配点,找到准确的特征匹配对作为计算单应矩阵的基础。GMS算法[20, 21]具有高鲁棒性、运行速度快等优点,可以在保证运算速度的前提下,获得更加精准的优秀特征点对。具体而言,GMS算法将运动平滑约束(来自不同视点的图像的相邻像素共享相似运动)结合到统计框架中以避免错误匹配。所以本文在使用暴力匹配算法计算特征点对后,通过GMS算法进一步得到筛选过后的优秀特征点对,以优秀特征点对作为RANSAC算法的输入,得到计算单应矩阵的内点。
由于使用了网格化对图像进行特征点匹配处理,GMS算法筛选粗匹配产生的特征点对后所产生的优秀特征点对仍然不够准确。针对此问题,在特征点粗匹配时,基于GMS-RANSAC算法采用双向匹配策略提高粗匹配的特征点对匹配准确率。具体来说,首先进行正向匹配,在使用BRISK算法在第一幅图像中提取特征点后,对特征点采用暴力匹配算法找到每个特征点在第二幅图像中的对应特征点,并对图中的特征点构造相应的匹配关系,例如第一张图像中的A点对应第二张图像中的B点。然后进行反向匹配,以第二张图像为参考,重复上述的过程,例如第二张图像中的B点对应第一张图像中的M点。最后,比较正向匹配和反向匹配的匹配结果,如果A点和M点相同,则认为这是一个有效的匹配,否则认为该匹配不成立。
1.2 结合最佳缝合线和改进渐入渐出融合算法的图像融合算法 1.2.1 基于动态规划思想的最佳缝合线算法针对拼接结果出现重影的问题,最佳缝合线算法[22, 23]是解决该问题的一种有效方法。如果在两幅图像的重叠区域中,存在一条色差强度以及梯度差异最小的缝合线,则称该缝合线为最佳缝合线,因为依此缝合线进行图像拼接,所产生的拼接影响最小。最佳缝合线算法的能量函数如下所示:
| $ E(x, y)=E_d(x, y)+E_S(x, y), $ | (7) |
式中,Ed(x, y)表示图像颜色差异强度值,ES(x, y)表示图像结构差异强度值,两者表达式如下:
| $ E_d(x, y)=I_L(x, y)-I_R(x, y), $ | (8) |
| $ E_S(x, y)=\nabla I_L(x, y)+\nabla I_R(x, y), $ | (9) |
其中,IL、IR分别为左图和右图中的重叠部分图像,▽为梯度差。
Ed(x, y)所表示的图像颜色差异强度值通常使用灰度图像来计算。为了找到图像中最小色彩的区域,本文采用HSV(Hue, Saturation, Value)色彩空间中的颜色饱和度差值来代替重叠区域灰度图像的原始色差强度,优化后的颜色差异强度值函数如下所示:
| $ E_d(x, y)=I_{L_S}(x, y)-I_{R_S}(x, y) 。$ | (10) |
研究表明,人眼的视觉特性导致人对图像中的梯度变化比亮度变化更加敏感,即人更容易被差异较大的边缘吸引,并会夸大这一差异,甚至影响自身的判断[24]。因此,本文在计算能量函数时对像素的强度差值和结构差值增加不同的权重,以提高梯度变化在缝合线选择上的权重:
| $ E(x, y)=\mu_1 E_d(x, y)+\mu_2 E_S(x, y), $ | (11) |
其中,μ1、μ2分别为强度差值和结构差值的不同权重,预设μ1=0.4,μ2=0.6。
同时,为了使缝合线尽可能处于图像拼接区域的中间位置,并且为了使在后续的渐入渐出融合算法中选取缝合线过渡区域不靠近图像边界,所以在上式的基础上增加中间项能量函数:
| $ E_C=\left[\cos \left(\frac{j}{R-L}+\frac{1}{2}\right) \pi\right]+1, $ | (12) |
式中,R、L分别为图像重叠部分的左、右边界值。该区域内的能量如图 2所示。

|
| 图 2 中间项能量图 Fig.2 Intermediate term energy diagram |
综上,本文中最佳缝合线算法的能量函数为
| $ E(x, y)=\mu_1 E_d(x, y)+\mu_2 E_S(x, y)+E_C 。$ | (13) |
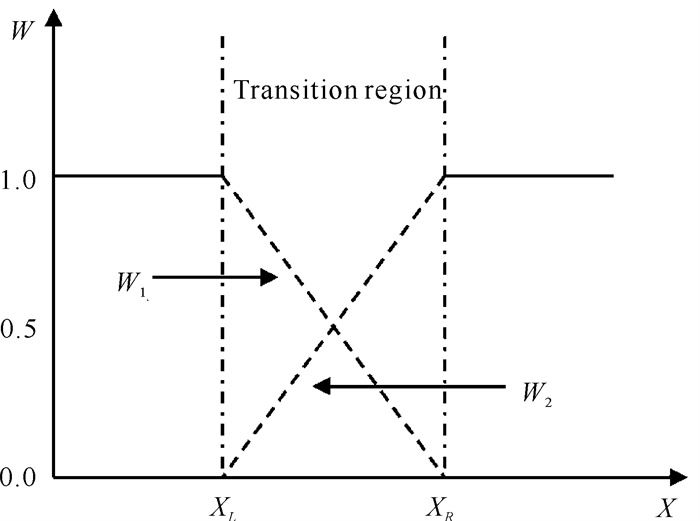
渐入渐出融合算法[25]是在直接平均融合算法的基础上改进的,主要是在图像重叠区域内像素融合部分增加了权值系数。像素点权值根据坐标位置关系计算,随着其靠近中央区域而变大。渐入渐出融合算法示意图(图 3)如下。
|
| 图 3 渐入渐出融合算法示意图 Fig.3 Schematic diagram of gradual-in and gradual-out weighted fusion algorithm |
假定要融合的两幅图像的左图像素点为L(x, y),右图像素点为R(x, y),拼接后的图像像素点为I(x, y),则渐入渐出融合算法的计算公式如下:
| $ \begin{gathered} I(x, y)= \\ \left\{\begin{array}{c} L(x, y), (x, y) \in L \\ W_1 L(x, y)+W_2 R(x, y), (x, y) \in(L \cap R), \\ R(x, y), (x, y) \in R \end{array}\right. \end{gathered} $ | (14) |
式中,W1、W2为两幅图重叠区域像素点(x, y)的加权系数,且W1+W2=1。W1、W2所对应的权重计算方式为
| $ \left\{\begin{array}{l} W_1(x, y)=\frac{X_R-x}{X_R-X_L} \\ W_2(x, y)=\frac{x-X_L}{X_R-X_L} \end{array}\right., $ | (15) |
式中,XR、XL分别为图像重叠区域的左、右边界。
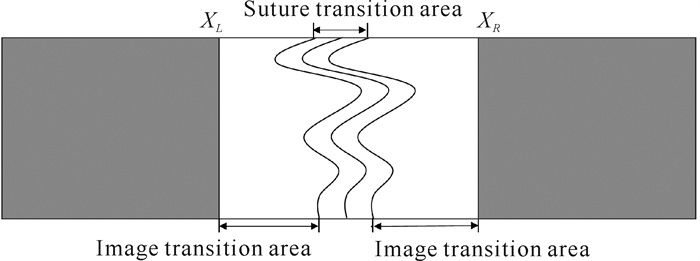
由于渐入渐出融合算法属于线性融合方法,无法实现图像在重叠区域中平滑过渡,容易造成重影以及缝合线处有明显拼接缝的问题。为此,针对渐入渐出融合算法的线性权重系数,本文提出一种权重具有非线性变化特性的改进渐入渐出融合算法进行图像融合,其基本思想:待两幅图像沿着求解所得的最佳拼接缝拼接后,利用改进的渐入渐出融合算法计算重叠区域相应的像素值,从而完成对图像的拼接融合(图 4)。具体来说,将拼接图像分为缝合线过渡区和图像过渡区,其中缝合线过渡区为将缝合线分别向左、右平移d个像素点,形成一个宽度为2d的区域,在区域中使用非线性渐入渐出融合算法进行图像拼接;图像过渡区为图像左右边界到拼接缝过渡区之间的图像区域。
|
| 图 4 融合区域示意图 Fig.4 Schematic diagram of fusion area |
在缝合线过渡区中所使用的非线性渐入渐出融合算法的权值计算公式为
| $ W_1^{\prime}=1-\frac{1}{2} \sqrt{1-\frac{x^2}{w^2}}, $ | (16) |
| $ W_2^{\prime}=1-W_1^{\prime}, $ | (17) |
| $ w=\frac{P_R-P_L}{2}, $ | (18) |
式中, W′1+W′2=1,PR、PL分别为缝合线左、右移动后的端点。在图像融合算法中,权重随着像素位置变化越慢,其融合效果越好,图像过渡越自然。
| $ \left|\frac{\partial W_1}{\partial x}\right|=\left|\frac{\partial W_2}{\partial x}\right|=\frac{1}{w}, $ | (19) |
| $ \left|\frac{\partial W_1^{\prime}}{\partial x}\right|=\left|\frac{\partial W_2^{\prime}}{\partial x}\right|=\frac{1}{2 w} \sqrt{\frac{1}{w^2-x^2}}, $ | (20) |
由式(19)和式(20)可知,当像素点靠近缝合线时,传统方法[式(19)]的瞬间变化率大于改进方法[式(20)]的瞬间变化率。而权重越小其融合效果越好,因此改进方法的融合效果更优越。
综上所述,本文改进的渐入渐出融合算法如下式所示:
| $ \begin{gathered} I(x, y)= \\ \left\{\begin{array}{c} L(x, y), x \leqslant P_L \\ W_1^{\prime} L(x, y)+W_2^{\prime} R(x, y), P_L <x <P_R, \\ R(x, y), x \geqslant P_R \end{array}\right. \end{gathered} $ | (21) |
式中, PL、PR分别为缝合线过渡区域的左、右边界。
2 实验与结果分析本文分别从图像匹配和拼接质量两个方面对提出的BRISK+GMS图像配准算法、最佳缝合线算法和改进的渐入渐出融合算法进行验证。实验运行环境采用CPU为Intel(R) Core(TM) i9-13900HX,内存为16 GB,64位Windows 11操作系统的个人计算机。本文所有算法基于OpenCV 4.8.0实现,编程环境为Visual Studio 2022。
2.1 图像配准算法实验结果分析本文采用BRISK算法进行特征点提取,并使用GMS-RANSAC算法进行特征点对的匹配筛选。为了验证该算法设计的匹配效率及匹配速度,将其与BRISK+RANSAC算法、SURF+GMS-RANSAC算法以及SURF+RANSAC算法进行对比试验。
实验所使用的图像为APAP数据集[9]中图像拼接相关的图像,如图 5所示。图像分辨率分别为2 000×1 329、3 264×2 448、2 000×1 329。实验结果如图 6所示,结果图中每一条线的端点为当前图中的特征点,线段表示两图中已经匹配到的特征点对。BRISK+GMS-RANSAC算法所提取到的特征点匹配对明显高于其余3种,具有良好的特征点匹配对提取效率。

|
| 图 5 实验图像 Fig.5 Experimental images |

|
| 图 6 特征匹配结果 Fig.6 Result of feature matching |
对于实验结果的分析,采用在提取相同基数特征点的情况下,使用图像配准阶段特征点提取所需时间、优秀特征点对匹配准确率(Correct Matching Rate, CMR)以及RANSAC算法筛选的内点数量3个评价指标对算法进行评价。其中优秀特征点对匹配准确率定义为
| $ \mathrm{CMR}=\frac{n_{\text {inliers }}}{n_{\text {sum }}}, $ | (22) |
式中,ninliers为内点的提取数量,nsum为粗匹配后的特征点对数量。
表 1为使用本文算法、BRISK+RANSAC算法、SURF+GMS-RANSAC算法和SURF+RANSAC算法得到的特征点检测数目、粗匹配后的特征点匹配数目以及经过RANSAC算法筛选后的内点数目。在特征点检测数目相似的情况下,本文算法提取到的内点数目最多,其次为SURF+GMS-RANSAC算法。由于内点数越多,所计算得到的单应矩阵越精确,所以在使用RANSAC算法进行内点计算前,使用GMS算法对暴力匹配算法得到的匹配对进行筛选,更有利于图像单应矩阵的计算。
| 组别 Group |
算法 Algorithms |
特征点检测数 Feature point count |
匹配点数 Matching point count |
内点数 Inlier count |
| 1 | BRISK+RANSAC | 24 500 | 29 | 14 |
| SURF+GMS-RANSAC | 29 641 | 12 694 | 4 644 | |
| SURF+RANSAC | 29 641 | 925 | 133 | |
| The algorithm of this article | 24 500 | 10 786 | 5 522 | |
| 2 | BRISK+RANSAC | 4 006 | 450 | 341 |
| SURF+GMS-RANSAC | 2 469 | 1 021 | 691 | |
| SURF+RANSAC | 2 469 | 26 | 16 | |
| The algorithm of this article | 4 006 | 1 011 | 830 | |
| 3 | BRISK+RANSAC | 21 670 | 472 | 226 |
| SURF+GMS-RANSAC | 28 310 | 11 358 | 3 552 | |
| SURF+RANSAC | 28 310 | 1 841 | 502 | |
| The algorithm of this article | 21 670 | 8 825 | 3 510 |
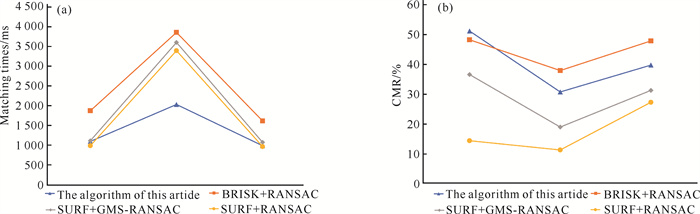
图 7为上述实验数据中本文算法、BRISK+RANSAC算法、SURF+GMS-RANSAC算法和SURF+RANSAC算法的图像配准时间以及特征点匹配效率。由图 7(a)可知,本文算法平均用时最少、速度最快,相较于BRISK+RANSAC、SURF+GMS-RANSAC、SURF+RANSAC 3种算法平均速率分别提升了77.9%、40.4%、29.7%;由于SURF+RANSAC算法所提取的特征点对有限,从而其平均速度略微优于另外两种算法;提取速度最慢的为BRISK+RANSAC算法。由图 7(b)可知,BRISK算法对于RANSAC内点的提取效率远高于SURF算法,同时由于BRISK+RANSAC算法提取的匹配点数目远低于本文算法,所以在匹配正确率方面略高于本文算法。本实验证明在RANSAC算法之前进行GMS算法粗匹配会增加内点的匹配准确率,从而提升图像配准阶段所计算的单应矩阵的精准程度。
|
| 图 7 测试图像运行结果 Fig.7 Test image running results |
2.2 图像融合算法实验结果分析
为了验证本文算法在图像融合中生成图像的质量,选取分辨率分别为1 260×300和1 100×300的两张智能化养殖车间的视差图像[图 8(a)],以及960×500和800×550的两张室外建筑视差图像[图 8(b)],并依次使用最佳缝合线+渐入渐出融合算法、区域化的渐入渐出融合算法以及本文算法进行对比分析,以验证算法对于室内外环境的图像拼接效果。

|
| 图 8 融合输入图像 Fig.8 Fused input images |
由图 9中的方框可以看出,利用最佳缝合线+渐入渐出融合算法会产生一定的重影问题;利用区域化的渐入渐出融合算法不仅没有解决重影问题的,而且还会产生一定的拼接缝。为了得到更高质量的拼接融合图像,本文优化了最佳缝合线算法中的能量函数以及渐入渐出融合算法中的权值函数,使得图像拼接融合时,过渡更加平滑,解决了重影和拼接缝等问题。

|
| 图 9 图像融合效果 Fig.9 Image fusion results |
为了客观评价融合后图像的质量,采用信息熵、平均梯度和标准差等客观评价指标对融合效果进行评价。表 2给出了基于信息熵、平均梯度和标准差的图像质量评价结果。其中,信息熵越大表明融合图像信息越丰富;平均梯度越大表示融合图像越清晰,图像融合部分过渡更加平滑;图像标准差越大表示图像像素离散程度越高,质量越好。
| 组别 Group |
融合算法 Fusion algorithm |
信息熵 Informational entropy |
平均梯度 Average gradient |
标准差 Standard deviation |
| 1 | Optimal seam algorithm with fade-in and fade-out weighted fusion | 6.549 8 | 112.254 0 | 51.053 4 |
| Regionalized fade-in and fade-out weighted fusion algorithm | 6.552 2 | 112.544 0 | 51.093 7 | |
| The algorithm of this article | 7.385 4 | 124.418 0 | 56.908 6 | |
| 2 | Optimal seam algorithm with fade-in and fade-out weighted fusion | 7.524 1 | 48.152 3 | 69.879 0 |
| Regionalized fade-in and fade-out weighted fusion algorithm | 7.617 2 | 49.601 9 | 69.929 7 | |
| The algorithm of this article | 7.625 6 | 49.939 9 | 70.378 2 |
由表 2可知,本文算法处理结果的信息熵、平均梯度和标准差上较其他算法处理结果有所提升。如表 2组别1中,本文算法处理结果的信息熵相较于其他两种算法分别提升0.835 59、0.833 21,平均梯度相较于其他两种算法分别提升12.164、11.874,标准差相较于其他两种算法分别提升5.855 2、5.814 9。综上所述,本文算法在图像融合过程中,所生成的全景具有更清晰、更平滑、像素效果更好的效果,并解决了图像融合过程中出现的拼接缝、重影等问题,保证了图像拼接过程中的图像质量。
3 结论本文针对图像配准阶段特征点提取效率问题以及匹配效率问题设计了一种BRISK+GMS-RANSAC组合式图像配准算法,该方法在通过BRISK算法进行特征点提取后,使用结合双向匹配策略的GMS-RANSAC算法进行优秀特征点对筛选,从而为后续图像融合阶段提供精准的单应矩阵。在图像融合阶段针对该阶段出现的拼接缝、重影等问题,提出一种结合最佳拼接缝算法的改进渐入渐出算法,将HSV色彩空间中的色彩饱和度代替色差强度输入最佳缝合线算法的能量函数中,同时为了使得缝合线过渡区尽量处于图像中央,在能量函数中添加中间项,使其在最佳缝合线算法计算时,找到贴近中央区域的最佳缝合线。此外,将渐入渐出融合算法分区,增加其运算效率,并改进加权函数,使得图像融合阶段图像过渡更加平滑。实验结果表明,本文算法在图像配准阶段能够保证各种图像类型的特征点提取效率及匹配效率,同时在图像融合阶段能够保证图像融合后图像的平滑度和质量。
| [1] |
中共中央, 国务院. 数字中国建设整体布局规划[EB/OL]. (2023-02-27)[2024-03-12]. https://www.gov.cn/zhengce/2023-02/27/content_5743484.htm.
|
| [2] |
农业农村部, 中央网络安全和信息化委员会办公室. 数字农业农村发展规划(2019-2025年)[EB/OL]. (2020-04-14)[2024-03-12]. http://www.moa.gov.cn/nybgb/2020/202002/202004/t20200414_6341532.htm.
|
| [3] |
于喆. 数字化海水养殖主要技术综述[J]. 中国水产, 2023(6): 55-56. |
| [4] |
韩世静, 苗书锋, 郝向阳, 等. 监控视频与地理信息融合技术发展综述[J]. 测绘通报, 2022(5): 1-6. |
| [5] |
杨松, 陈崇成. 面向实景三维模型和实时视频图像融合的纹理映射[J]. 测绘通报, 2023(10): 61-66. |
| [6] |
MA W, WANG K, LI J, et al. Infrared and visible image fusion technology and application: a review[J]. Sensors, 2023, 23(2): 599. DOI:10.3390/s23020599 |
| [7] |
BROWN M, LOWE D G. Automatic panoramic image stitching using invariant features[J]. International Journal of Computer Vision, 2007, 74(1): 59-73. DOI:10.1007/s11263-006-0002-3 |
| [8] |
MANDA S C, MUTTINENI S, VENKATACHALAM G, et al. Image stitching using RANSAC and bayesian refinement[C]//2023 3rd International Conference on Intelligent Technologies (CONIT). Piscataway, NJ: IEEE, 2023: 1-5.
|
| [9] |
ZARAGOZA J, CHIN T J, BROWN M S, et al. As-projective-as-possible image stitching with moving DLT[C]//2013 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2013: 2339-2346.
|
| [10] |
LIN C C, PANKANTI S U, RAMAMURTHY K N, et al. Adaptive as-natural-as-possible image stitching[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway, NJ: IEEE, 2015: 1155-1163.
|
| [11] |
江智, 江德港, 黄子杰, 等. 基于IB-SURF算法的无人机图像拼接技术研究[J]. 计算机工程与应用, 2024, 60(3): 263-269. |
| [12] |
LING C D, QIN H K, TAO Q, et al. A real-time video fusion processing system based on SIFT algorithm and FPGA[C]//2019 IEEE 2nd International Conference on Automation, Electronics and Electrical Engineering (AUTEEE). Piscataway, NJ: IEEE, 2019: 499-503.
|
| [13] |
WANG K, YANG T, ZHANG X H, et al. An improved ultra-high definition panoramic video mosaic method for airport scene[C]//2022 IEEE 8th International Conference on Computer and Communications (ICCC). Piscataway, NJ: IEEE, 2022: 2076-2080.
|
| [14] |
张望成, 杨建永, 胡炎. 一种快速鲁棒性的视差图像拼接方法[J]. 无线电工程, 2024, 54(3): 653-659. |
| [15] |
崔志远. 基于网格变形的无人机图像拼接技术研究[D]. 南昌: 南昌大学, 2023.
|
| [16] |
武忆涵. 基于自适应接缝线和快速融合的全景视频拼接技术研究[D]. 西安: 长安大学, 2023.
|
| [17] |
LEUTENEGGER S, CHLI M, SIEGWART R Y. BRISK: binary robust invariant scalable keypoints[C]//2011 International Conference on Computer Vision. Piscataway, NJ: IEEE, 2011: 2548-2555.
|
| [18] |
FENG D M, FENG M Q. Computer vision for SHM of civil infrastructure: from dynamic response measurement to damage detection: a review[J]. Engineering Structures, 2018, 156: 105-117. DOI:10.1016/j.engstruct.2017.11.018 |
| [19] |
GEHRIG D, REBECQ H, GALLEGO G, et al. EKLT: asynchronous photometric feature tracking using events and frames[J]. International Journal of Computer Vision, 2020, 128(3): 601-618. DOI:10.1007/s11263-019-01209-w |
| [20] |
BIAN J W, LIN W Y, LIU Y, et al. GMS: grid-based motion statistics for fast, ultra-robust feature correspondence[J]. International Journal of Computer Vision, 2020, 128(6): 1580-1593. DOI:10.1007/s11263-019-01280-3 |
| [21] |
LAN X Y, GUO B L, HUANG Z, et al. An improved UAV aerial image mosaic algorithm based on GMS-RANSAC[C]//2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP). Piscataway, NJ: IEEE, 2020: 148-152.
|
| [22] |
XIU C B, FANG J Y, ZHANG J. Image stitching method based on adaptive weighted fusion[C]//2021 33rd Chinese Control and Decision Conference (CCDC). Piscataway, NJ: IEEE, 2021: 3099-3103.
|
| [23] |
PENG Z, MA Y, MEI X, et al. Hyperspectral image stitching via optimal seamline detection[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. |
| [24] |
杨威, 赵剡, 许东. 基于人眼视觉的结构相似度图像质量评价方法[J]. 北京航空航天大学学报, 2008, 34(1): 1-4. |
| [25] |
罗永涛, 王艳, 张红民. 结合最佳缝合线和改进渐入渐出法的图像拼接算法[J]. 红外技术, 2018, 40(4): 382-387. |


