2. 广西师范大学生命科学学院, 广西桂林 541006
2. College of Life Science, Guangxi Normal University, Guilin, Guangxi, 541006, China
株高、胸径和冠幅是表征林木生长状况的重要指标,在森林资源调查和森林经营中是重要的测树因子[1-4]。通过实测数据建立测树因子相关生长模型,利用胸径、株高等相对容易测定的因子来估算其他因子的数量特征是一种较好的间接方法,不仅可以定量地了解它们的生长性质,还可以进行统计和预测[5]。测树因子间常用的回归模型有线性、对数曲线、逆曲线、二次曲线、复合曲线、幂曲线、增长曲线等[1, 6]。此外,通过通径分析还可以揭示株高、胸径、冠幅等测树因子的相互作用和影响规律,为目标树种的定向管理提供科学依据[7, 8]。
罗浮柿(Diospyros morrisiana)是柿科(Ebenaceae)柿属(Diospyros)常绿乔木树种,在我国自然分布于广西、广东、福建、浙江、贵州、云南、四川、台湾等地,在广西各地均有分布。目前,关于罗浮柿的研究主要有种群分布格局及关联分析[9]、育种和育苗[10, 11]、凋落物对种子萌发的影响[12]、粗木质残体特征[13]等,而对其测树因子方面的研究尚未见有文献报道。因此,本研究以防城季节性雨林优势种罗浮柿为研究对象,探究其株高、胸径、冠幅之间的相互联系,并建立株高、胸径、冠幅之间的回归模型,以掌握其形态特征及生长规律,为保护管理以罗浮柿为优势种的季节性雨林提供理论依据。
1 材料与方法 1.1 研究地概况研究地设在广西防城金花茶国家级自然保护区那山子季节性雨林鹅掌柴+罗浮柿群落内。该保护区地处十万大山南麓蓝山支脉(108°01′57″-108°12′42″E,21°43′55″-21°49′36″N);气候属热带季风气候,全年温和湿润,冬短夏长,年均气温21.8 ℃,年均降水量2 900 mm;区域植被类型以常绿林为主。研究地海拔约290 m,所在群落高12-16 m,盖度85%以上。乔木层组成种类有鹅掌柴(Heptapleurum heptaphyllum)、罗浮柿、两广梭罗树(Reevesia thyrsoidea)、黄樟(Camphora parthenoxylon)、假苹婆(Sterculia lanceolata)、白楸(Mallotus paniculatus)、打铁树(Myrsine linearis)、大果榕(Ficus auriculata)、银柴(Aporosa dioica)等。灌木层由灌木和上层乔木幼树共同组成,灌木种类有大管(Micromelum falcatum)、栀子(Gardenia jasminoides)、柏拉木(Blastus cochinchinensis)等。草本层稀疏,组成种类有刺头复叶耳蕨(Arachniodes aristata)、山姜(Alpinia japonica)、露兜草(Pandanus austrosinensis)等。层间植物有瓜馥木(Fissistigma oldhamii)、买麻藤(Gnetum montanum)、白粉藤(Cissus repens)、牛果藤(Nekemias cantoniensis)等。
1.2 研究对象及株高、胸径、冠幅测定在防城那山子季节性雨林中设置1 hm2群落样地,选择群落优势种罗浮柿为研究对象,对其胸径≥1 cm的个体进行每木检尺,测量株高(H)、胸径(D)、冠幅(W)等因子的数量特征。其中,冠幅为东西向冠幅长度(W1)和南北向冠幅长度(W2)的平均值,即W=(W1+W2)/2。对株高、胸径和冠幅进行频数分布统计,间隔分别为2 m、5 cm和1 m。
1.3 变量间相关性检验采用Pearson相关系数来衡量两个变量间的线性相关程度和相关方向。相关系数(r)的值域为[-1, 1],正值表示正相关,越趋近于1,则表示变量间的正相关性越强;负值表示负相关,越趋近于-1,则表示变量间的负相关性越强;等于0则表示无相关。r的计算公式如下:
| $ r=\frac{\sum\limits_{i=1}^N\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum\limits_{i=1}^N\left(x_i-\bar{x}\right)^2 \sum\limits_{i=1}^N\left(y_i-\bar{y}\right)^2}}, $ |
式中,x和y分别为两个变量的平均值,N为样本总数。
1.4 回归模型及模型评价采用y=a+bx(线性模型,Linear model)、y=a+blnx(对数曲线模型,Logarithmic curve model)、y=a+b/x(逆曲线模型,Inverse curve model)、y=a+bx+cx2(二次曲线模型,Quadratic curve model)、y=abx(复合曲线模型,Composite curve model)、y=axb(幂曲线模型,Power curve model)、y=ea+b/x(S形曲线模型,S-shaped curve model)、y=ea+bx(增长曲线模型,Growth curve model)和y=aebx(指数曲线模型,Exponential curve model)等9种模型进行回归分析[14]。同时,以冠幅为因变量,株高和胸径为自变量进行逐步回归分析。采用决定系数(R2)对模型进行评价,计算公式如下:
| $ R^2=1-\frac{\sum\limits_{i=1}^n\left(\hat{y}_i-y_i\right)^2}{\sum\limits_{i=1}^n\left(y_i-\bar{y}\right)^2}, $ |
式中,n表示样本数量;yi和
以株高、胸径为自变量,冠幅为因变量进行通径分析,揭示株高和胸径2个生长因子对冠幅的作用方式,即直接作用或者间接作用。
1.6 统计分析采用Excel 2023和SPSS 22.0软件对野外取样数据进行整理和分析。
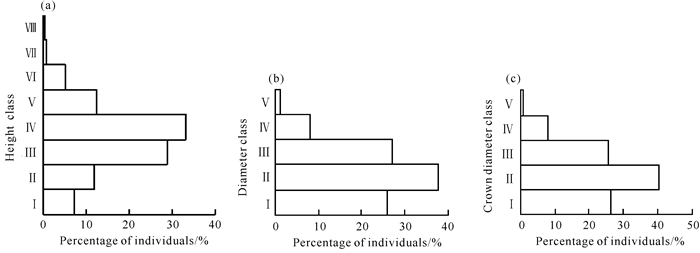
2 结果与分析 2.1 测树因子统计量在防城那山子季节性雨林1 hm2群落样地中罗浮柿个体有385株。由表 1和图 1可知,株高平均值为7.8 m,最大值为16.0 m,株高8-10 m的个体最多,占个体总数的33.2%;株高6-8 m的个体也较多,占个体总数的28.8%。胸径平均值为8.5 cm,最大值为24.0 cm,以胸径5-10 cm的个体最多,占个体总数的37.9%。冠幅平均值为2.1 m,最大值为4.5 m,以冠幅1.5-2.5 cm的个体最多,占个体总数的40.3%。
| 变量 Variable |
最大值 Maximum value |
最小值 Minimum value |
平均值 Average value |
中位数 Median |
众数 Mode |
偏度 Skewness |
标准差 Standard deviation |
变异系数 Coefficient of variation |
| H/m | 16.0 | 2.0 | 7.8 | 8.0 | 7.5 | 0.069 | 2.438 | 0.31 |
| D/cm | 24.0 | 1.1 | 8.5 | 8.5 | 7.5 | 0.404 | 4.422 | 0.52 |
| W/m | 4.5 | 0.5 | 2.1 | 2.0 | 2.3 | 0.363 | 0.847 | 0.40 |
|
| 图 1 罗浮柿测树因子的频数分布 Fig.1 Frequency distribution of tree measurement factors of D.morrisiana |
2.2 胸径与株高回归分析
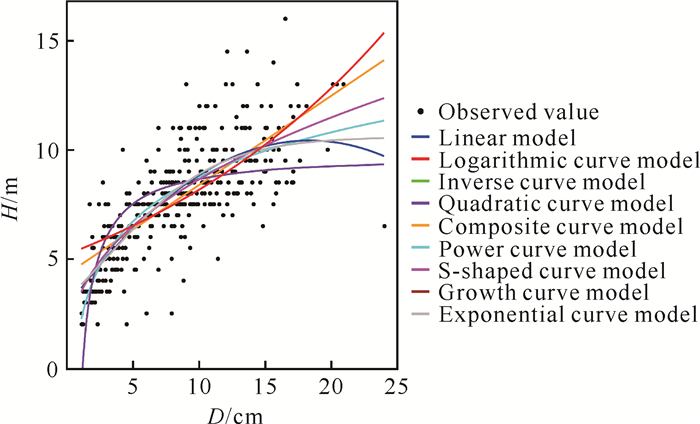
罗浮柿胸径与株高之间呈正相关关系,即随着胸径的增加,株高呈增加趋势(图 2)。Pearson相关性分析得出,r=0.742,P=0.000 < 0.01,即胸径与株高之间的正相关达到极显著水平。采用9种曲线模型对罗浮柿胸径与株高的关系进行拟合,结果如表 2所示。各拟合方程的R2为0.497-0.634,它们均在0.01水平上极显著相关,以幂曲线模型拟合最优,表达式为H=3.0248×D0.4501,R2=0.634。
|
| 图 2 罗浮柿胸径与株高的拟合曲线 Fig.2 Fitting curve of diameter at breast height and tree height of D.morrisiana |
| 模型类型 Type of model |
回归方程 Regression equation |
N | R2 | F | P |
| Linear model | H=4.2996+0.4089D | 385 | 0.550 | 468.242 | 0.000 |
| Logarithmic curve model | H=1.9721+2.9476lnD | 385 | 0.600 | 575.154 | 0.000 |
| Inverse curve model | H=9.8167-11.5694/D | 385 | 0.497 | 378.472 | 0.000 |
| Quadratic curve model | H=2.7748+0.8330D-0.0226D2 | 385 | 0.600 | 287.039 | 0.000 |
| Composite curve model | H=4.4447×1.0607D | 385 | 0.518 | 411.445 | 0.000 |
| Power curve model | H=3.0248×D0.4501 | 385 | 0.634 | 662.355 | 0.000 |
| S-shaped curve model | H=e2.3269-1.8905/D | 385 | 0.601 | 575.845 | 0.000 |
| Growth curve model | H=e1.4917+0.0589D | 385 | 0.518 | 411.445 | 0.000 |
| Exponential curve model | H=4.4447e0.0590D | 385 | 0.518 | 411.445 | 0.000 |
2.3 胸径与冠幅回归分析
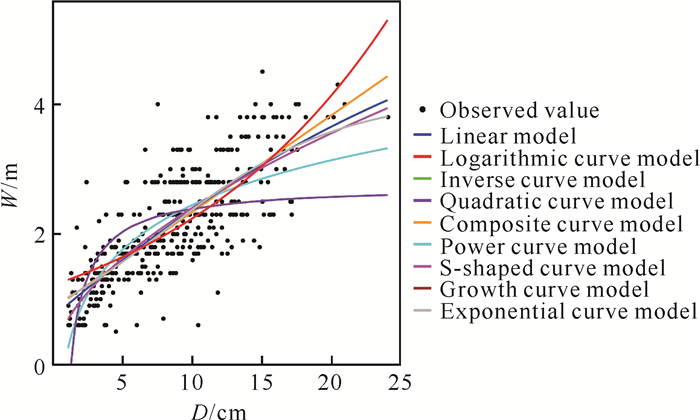
罗浮柿胸径与冠幅之间呈正相关关系,即随着胸径的增加,冠幅呈增加趋势(图 3)。Pearson相关性分析得出,r=0.780,P=0.000 < 0.01,即胸径与冠幅之间的正相关达到极显著水平。采用9种曲线模型对罗浮柿胸径与冠幅的关系进行拟合,结果如表 3所示。各拟合方程的R2为0.404-0.613,它们均在0.01水平上极显著相关,以幂曲线模型拟合最优,表达式为W=0.6600×D0.5462,R2=0.613。
|
| 图 3 罗浮柿胸径与冠幅拟合曲线 Fig.3 Fitting curve of diameter at breast height and crown diameter of D.morrisiana |
| 模型类型 Type of model |
回归方程 Regression equation |
N | R2 | F | P |
| Linear model | W=0.8475+0.1493D | 385 | 0.608 | 594.133 | 0.000 |
| Logarithmic curve model | W=0.1525+0.9976lnD | 385 | 0.570 | 507.312 | 0.000 |
| Inverse curve model | W=2.7559-3.6249/D | 385 | 0.404 | 259.989 | 0.000 |
| Quadratic curve model | W=0.7203+0.1847D-0.0019D2 | 385 | 0.611 | 299.934 | 0.000 |
| Composite curve model | W=1.0095×1.0795D | 385 | 0.573 | 513.751 | 0.000 |
| Power curve model | W=0.6600×D0.5462 | 385 | 0.613 | 607.041 | 0.000 |
| S-shaped curve mode | W=e1.0356-2.1303/D | 385 | 0.501 | 385.038 | 0.000 |
| Growth curve model | W=e0.0094+0.0765D | 385 | 0.573 | 513.751 | 0.000 |
| Exponential curve model | W=1.0095e0.0765D | 385 | 0.573 | 513.751 | 0.000 |
2.4 株高与冠幅回归分析
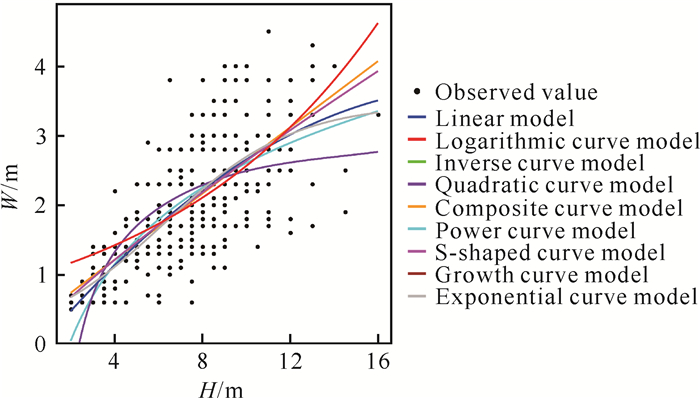
罗浮柿株高与冠幅之间呈正相关关系,即随着株高的增加,冠幅呈增加趋势(图 4)。Pearson相关性分析得出,r=0.685,P=0.000 < 0.01,即株高与冠幅之间的正相关达到极显著水平。采用9种曲线模型对罗浮柿株高与冠幅的关系进行拟合,结果如表 4所示。各拟合方程的R2为0.385-0.545,它们均在0.01水平上极显著相关,以幂曲线模型拟合最优,表达式为W=0.3147×H0.9108,R2=0.545。
|
| 图 4 罗浮柿株高与冠幅拟合曲线 Fig.4 Fitting curve of tree height and crown diameter of D.morrisiana |
| 模型类型 Type of model |
回归方程 Regression equation |
N | R2 | F | P |
| Linear model | W=0.2645+0.2380H | 385 | 0.470 | 338.996 | 0.000 |
| Logarithmic curve model | W=-1.0547+1.5905lnH | 385 | 0.463 | 330.536 | 0.000 |
| Inverse curve model | W=3.2539-7.7594/H | 385 | 0.385 | 239.462 | 0.000 |
| Quadratic curve model | W=-0.2534+0.3842H-0.0093H2 | 385 | 0.479 | 175.405 | 0.000 |
| Composite curve model | W=0.7048×1.1385H | 385 | 0.501 | 384.262 | 0.000 |
| Power curve model | W=0.3147×H0.9108 | 385 | 0.545 | 459.362 | 0.000 |
| S-shaped curve mode | W=e1.3485-4.6976/H | 385 | 0.506 | 392.544 | 0.000 |
| Growth curve model | W=e0.3498+0.1298H | 385 | 0.501 | 384.262 | 0.000 |
| Exponential curve model | W=0.7048e0.1298H | 385 | 0.501 | 384.262 | 0.000 |
2.5 通径分析
罗浮柿的胸径、株高对冠幅均呈现极显著的正向作用,即随着胸径和株高的增大,冠幅逐渐增大(表 5)。胸径直接影响株高和冠幅,影响系数分别为0.742和0.604;株高直接影响冠幅,影响系数为0.238。胸径还可通过对株高的作用间接影响冠幅,这些影响都是明显的正向促进作用。
| X | Y | 非标准化系数 Non-standardized coefficients |
标准化系数 Standardized coefficients |
标准误 Standard error |
组合信度 Composite reliability |
P |
| D | H | 0.409 | 0.742 | 0.019 | 21.694 | 0.000 |
| D | W | 0.116 | 0.604 | 0.009 | 13.120 | 0.000 |
| H | W | 0.083 | 0.238 | 0.016 | 5.163 | 0.000 |
3 讨论 3.1 测树因子相关生长及回归模型
植物异速生长(Allometric scaling)是描述植物某些属性之间的非线性数量关系,反映个体不同方面性状的相关程度,通常以幂函数的形式来定量表征[15-17],并可通过测定某些易测量的指标来估算较难测量的指标,因而在理论研究和生产实践中都具有重要的意义[5, 6]。在野外调查中,通过观测样地中部分立木胸径,利用胸径-株高关系模型来估算样地内未观测立木株高,可降低调查立木数据的成本[18-20]。目前,在乔木树种调查中,已有许多线性或非线性模型被用来描述测树因子之间的关系[3, 20-22],其中株高、胸径、密度、断面积等是相对比较容易观测的测树因子,将这些因子加入到基础模型中可提高模型的精度及适用性[20]。本研究中Pearson相关性分析结果表明,防城季节性雨林优势种罗浮柿的株高、胸径、冠幅之间均呈极显著相关。通过线性、对数曲线、逆曲线、二次曲线、复合曲线、幂曲线、S形曲线、增长曲线、指数曲线等9种函数模型拟合分析得出,罗浮柿胸径-株高、胸径-冠幅、株高-冠幅的拟合效果均较好,在0.01水平上极显著相关,其中以幂曲线模型拟合方程最优,这与刘春云等[3]、张连金等[21]、胡波等[22]的研究结果相似。胸径是测定方便、快速、准确度高的指标,因此基于罗浮柿胸径-株高、胸径-冠幅最优模型可以获得其株高、冠幅等相对不易准确测量的指标数据。
3.2 测树因子间的直接作用和间接作用通径分析能客观地反映各影响因素对某一特定测树因子直接作用和间接作用的大小,能补充和拓展回归分析、相关分析的统计学功能,是一种简单、实用、较为理想的评价方法。在防城季节性雨林中,罗浮柿各生长因子之间的关系较为复杂,不能仅通过相关性分析和回归分析来判断罗浮柿株高、胸径和冠幅三者之间的关系及影响,还要通过通径分析进一步研究自变量与因变量之间的数量关系,即将株高、胸径和冠幅之间的相关系数分解为直接通径系数和间接通径系数,因而通径分析不仅克服了不同自变量对因变量不能直接比较的问题,而且达到了准确表现自变量与因变量之间关系的目的,从而揭示罗浮柿的株高、胸径对冠幅的影响大小。本研究中通径分析结果表明,罗浮柿胸径直接影响株高和冠幅,株高直接影响冠幅;胸径对株高的影响大于胸径对冠幅的影响,胸径对冠幅的影响大于株高对冠幅的影响;胸径还可通过对株高的作用间接地影响冠幅,这与赵保国等[7]、魏海英等[8]的研究结果相似。
4 结论防城季节性雨林优势种罗浮柿的最优相关生长模型为幂曲线模型,该模型不仅精度高,而且相关指标易于测定,完全适用于定量描述罗浮柿株高、胸径、冠幅之间的相关生长关系,并可为该地区森林群落中其他优势种的同类研究提供借鉴,为能够及时掌握季节性雨林林木生长状况提供科学的研究手段。
| [1] |
周欢, 乐祥明, 郭国志, 等. 太子山几种阔叶树种测树因子相关性分析[J]. 湖北林业科技, 2022, 51(1): 9-12, 31. |
| [2] |
COLBERT K C, LARSEN D R, LOOTENS J R. Height-diameter equations for thirteen midwestern bottomland hardwood species[J]. Northern Journal of Applied Forestry, 2002, 19(4): 171-176. DOI:10.1093/njaf/19.4.171 |
| [3] |
刘春云, 方文静, 蔡琼, 等. 中国落叶松林胸径-树高相关关系的探讨[J]. 北京大学学报(自然科学版), 2017, 53(6): 1081-1088. |
| [4] |
HUANG U S, TITUS S J, WIENS D P. Comparison of nonlinear height-diameter functions for major Alberta tree species[J]. Canadian Journal of Forest Research, 1992, 22(9): 1297-1304. DOI:10.1139/x92-172 |
| [5] |
梁士楚. 秋茄幼苗的形态特征及其生物量[J]. 武汉植物学研究, 1997, 15(2): 108-112. |
| [6] |
李栋梁, 钟琼芯, 蔡昌运, 等. 洋浦古树名木资源特征及测树因子相关性分析[J]. 分子植物育种, 2022, 20(16): 5495-5505. |
| [7] |
赵保国, 朱江, 艾训儒, 等. 水杉原生种群胸径树高与树冠的通径分析[J]. 东北林业大学学报, 2021, 49(10): 16-20. |
| [8] |
魏海英, 王博, 张维. 新疆野核桃自然保护区分枝成株野核桃胸径树高与冠幅的通径分析[J]. 经济林研究, 2023, 41(2): 120-128. |
| [9] |
廖南燕, 陈善栋, 李武峥, 等. 防城金花茶国家级自然保护区罗浮柿种群空间分布格局及关联分析[J]. 安徽农业科学, 2024, 52(1): 121-124. |
| [10] |
杨理兵, 赵成. 罗浮柿的培育[J]. 湖南林业, 2010(6): 33. |
| [11] |
张德明, 陈章和. 不同光强下几种南亚热带森林乔木的种子萌发和幼苗生长观察[J]. 生态科学, 1996, 15(2): 6-12. |
| [12] |
刘晋仙, 郭庆学, 王玉平, 等. 竹类凋落叶对4种乔木树种种子萌发的影响[J]. 林业科学, 2013, 49(1): 33-40. |
| [13] |
樊小丽, 周光益, 赵厚本, 等. 岭南藜蒴栲-罗浮柿群系粗木质残体的基本特征[J]. 林业科学研究, 2016, 29(3): 448-454. |
| [14] |
李志辉, 罗平. SPSS常用统计分析教程: SPSS 22.0中英文版[M]. 4版. 北京: 电子工业出版社, 2015.
|
| [15] |
韩文轩, 方精云. 幂指数异速生长机制模型综述[J]. 植物生态学报, 2008, 32(4): 951-960. |
| [16] |
张瑞昌, 岳明. 异速生长模型及其应用概述[J]. 生物学通报, 2011, 46(8): 6-9. |
| [17] |
NIKLAS K J. Plant allometry: the scaling of form and process[M]. Chicago: University of Chicago Press, 1994.
|
| [18] |
MEHTÄTALO L, DE-MIGUEL S, GREGOIRE T G. Modeling height-diameter curves for prediction[J]. Canadian Journal of Forest Research, 2015, 45(7): 826-837. DOI:10.1139/cjfr-2015-0054 |
| [19] |
ARABATZIS A A, BURKHART H E. An evaluation of sampling methods and model forms for estimating height-diameter relationships in loblolly pine plantations[J]. Forest Science, 1992, 38(1): 192-198. DOI:10.1093/forestscience/38.1.192 |
| [20] |
王冬至, 张冬燕, 张志东, 等. 基于非线性混合模型的针阔混交林树高与胸径关系[J]. 林业科学, 2016, 52(1): 30-36. |
| [21] |
张连金, 孙长忠, 辛学兵, 等. 北京九龙山不同林分树高与胸径相关生长关系分析[J]. 中南林业科技大学学报, 2014, 34(12): 66-70. |
| [22] |
胡波, 钟全林, 程栋梁, 等. 刨花楠树高与胸径异速生长的关系[J]. 沈阳大学学报(自然科学版), 2012, 24(3): 9-14. |



