2. 广西壮族自治区防城金花茶国家级自然保护区管理中心, 广西防城港 538021
2. Guangxi Fangcheng Golden Camellia National Nature Reserve Management Center, Fangchenggang, Guangxi, 538021, China
空间异质性(Spatial heterogeneity)是指生态学过程和格局在空间分布上的不均匀性及其复杂性[1]。由于群落内生境条件的差异,导致植物种群空间分布存在异质性,而空间异质性及空间格局是种群结构和动态变化的基础。地统计学方法适用于空间上既有随机性也有结构性的区域化变量研究,它不仅考虑了变量个体的属性、坐标和彼此间距离,对变量空间异质性的程度、组成、尺度、方向进行定量化描述,而且还可对空间格局进行模拟和预测[2, 3],因而被广泛应用于生态学研究,成为研究空间尺度依赖性和空间变异的主要方法[4, 5]。株高、胸径、冠幅、断面积、密度等指标是林木重要的测量因子,具有时空变化的特性,在空间上具有一定的随机性和格局结构,因而不少学者已应用地统计学理论和方法就上述指标开展相关研究,以弥补传统生态学认识的局限性[6-9]。季节性雨林是防城的地带性植被类型,对防城季节性雨林的研究目前主要有群落类型[10]、种类组成[10, 11]、层次结构[10]、个体空间散点图[11]、物种多样性[12]、种间联结性[12],以及罗浮柿(Diospyros morrisiana)种群空间分布格局及关联分析[13]等方面,而有关群落优势种群的空间异质性研究较少。鹅掌柴(Heptapleurum heptaphyllum)群落是防城季节性雨林的主要群落类型,因此本研究以株高为关键指标,采用地统计学方法分析该群落主要树种株高的空间异质性特征,旨在阐明在季节性雨林生境条件下组成树种的空间分布特点及其动态,为防城季节性雨林的有效保护和管理提供理论基础。
1 材料与方法 1.1 研究地概况研究地设在广西防城金花茶国家级自然保护区妹仔田季节性雨林鹅掌柴群落中。该保护区地处十万大山南麓蓝山支脉,东经108°01′57″-108°12′42″,北纬21°43′55″-21°49′36″。全年属热带季风气候,温和湿润,冬短夏长,年均气温21.8 ℃,年均降水量2 900 mm。区域植被类型以常绿林为主。样地群落高12-18 m,盖度85%以上。乔木层组成种类主要有鹅掌柴、枫香树(Liquidambar formosana)、肉实树(Sarcosperma laurinum)、罗浮柿、中华杜英(Elaeocarpus chinensis)、假苹婆(Sterculia lanceolata)、银柴(Aporosa dioica)、黄椿木姜子(Litsea variabilis)、棋子豆(Archidendron robinsonii)等。灌木层组成种类主要有罗伞树(Ardisia quinquegona)、九节(Psychotria asiatica)、杜茎山(Maesa japonica)、大管(Micromelum falcatum)、毛果算盘子(Glochidion eriocarpum)、野牡丹(Melastoma malabathricum)、柏拉木(Blastus cochinchinensis)等。草本层组成种类主要有半边旗(Pteris semipinnata)、露兜草(Pandanus austrosinensis)、长囊薹草(Carex harlandii)等。此外,层间植物较为发达,种类有扁担藤(Tetrastigma planicaule)、油麻藤(Mucuna sempervirens)、瓜馥木(Fissistigma oldhamii)、买麻藤(Gnetum montanum)、海南崖豆藤(Millettia pachyloba)、石柑子(Pothos chinensis)、海南海金沙(Lygodium circinnatum)等。
1.2 样地设置及群落学调查在季节性雨林鹅掌柴群落内的典型地段设置1个1 hm2样地,并将其划分为100个10 m×10 m的小样方。以小样方为基本单元,对样方内所有胸径(DBH)≥1 cm的木本植物进行每木调查,内容包括种名、株高(H)、胸径(DBH)、冠幅(W)、空间位置(X,Y)等特征指标。根据群落学调查结果,选择鹅掌柴、肉实树、银柴、黄椿木姜子、罗伞树和九节6个主要树种作为研究对象。
1.3 半方差函数的计算根据Matheron[3]的定义,半方差函数γ(h)的计算公式为
| $ \gamma(h)=\frac{1}{2 N(h)} \sum\limits_{i=1}^{N(h)}\left[Z\left(x_i\right)-Z\left(x_i+h\right)\right]^2, $ |
式中,Z(xi)和Z(xi+h)分别为区域化变量Z在空间位置xi和xi+h处的取值,N(h)是取样间隔为h时的样本对总数。
1.4 半方差函数曲线及其拟合以h为横坐标、γ(h)为纵坐标绘制半方差函数曲线图,采用线性模型、球状模型、指数模型和高斯模型对其进行拟合,以决定系数(R2)最大、残差(RSS)最小为原则确定最优模型[2-4]。根据模型中的块金值(C0)、基台值(C0+C)、变程(α)、块金值与基台值之比[C0/(C0+C)]、结构方差比[C/(C0+C)]等参数(其中,C为结构方差),定量分析区域化变量的空间分布特征。
1.5 克里金(Kriging)空间插值及种群空间格局复杂程度分析Kriging插值法是根据变量的取样数据和变异函数的结构特点,对未取样点的变量进行局部线性无偏最优估计[3-5],其表达式如下:
| $ Z\left(x_0\right)=\sum\limits_{i=1}^n \lambda_i Z\left(x_i\right), $ |
式中,Z(x0)表示未取样点的值;Z(xi)表示未取样点周围已知取样点的值;n为已知取样点的个数;λi为第i个取样点的权重。根据种群Kriging空间插值图以及格局类型、分形维数,分析种群空间格局的复杂程度及种群间的差异性。
1.6 统计分析采用GS+10.0软件进行地统计学分析[14],ade4软件来判断种群格局类型[15, 16],ImageJ 1.52a软件来计测Kriging插值法形成的空间格局的分形维数(D)[17]。
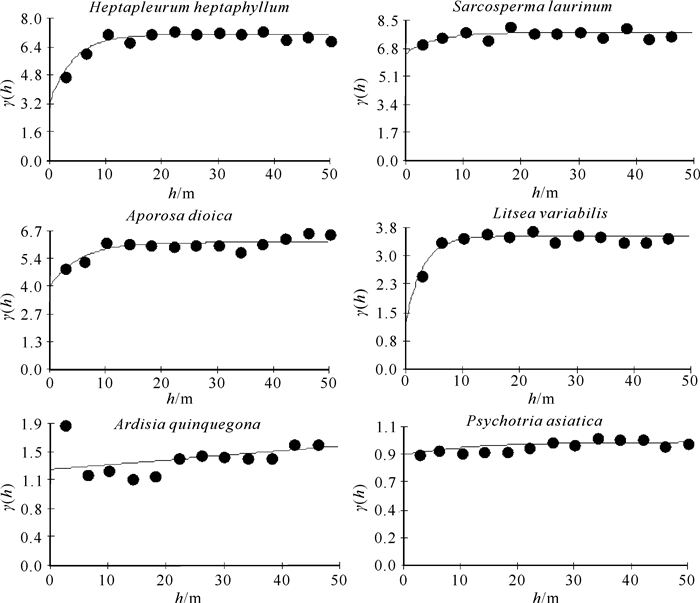
2 结果与分析 2.1 株高空间异质性程度根据图 1和表 1,在防城季节性雨林鹅掌柴群落中,鹅掌柴、肉实树、银柴和黄椿木姜子株高的半方差函数曲线符合指数模型,而罗伞树和九节符合直线模型。这6个主要树种株高的空间异质性程度可用块金值和基台值来度量。其中,块金值反映最小抽样尺度以下变量的变异性及测量误差,6个主要树种株高的块金值最小为0.876,最大为6.506,呈肉实树>银柴>鹅掌柴>黄椿木姜子>罗伞树>九节。t-检验表明,除鹅掌柴-银柴、黄椿木姜子-罗伞树2个种对外,其余13个种对间的块金值差异显著(表 2),说明鹅掌柴-银柴、黄椿木姜子-罗伞树在小尺度上具有相同或相似的生态学过程,因此它们的块金值差异不显著。基台值为半方差函数随着间距递增到一定程度时出现的平稳值,基台值越大表示总空间异质性程度越高,6个主要树种株高的基台值最小为0.977,最大为7.751,表现为肉实树>鹅掌柴>银柴>黄椿木姜子>罗伞树>九节(表 1),它们之间差异均显著(表 3)。
|
| 图 1 鹅掌柴群落主要树种株高的半方差函数曲线 Fig.1 Semi-variance function curves of plant heights of main tree species in H.heptaphyllum community |
| 种名 Species name |
理论模型 Theoretical model |
C0 | C0+C | C0/(C0+C) | C/(C0+C) | α/m | RSS | R2 | D |
| Heptapleurum heptaphyllum | Exponential model | 3.279 | 7.099 | 0.462 | 0.538 | 12.8 | 0.690 | 0.901 | 1.429 6 |
| Sarcosperma laurinum | Exponential model | 6.506 | 7.751 | 0.839 | 0.161 | 14.7 | 1.130 | 0.292 | 1.411 6 |
| Aporosa dioica | Exponential model | 4.007 | 6.148 | 0.652 | 0.348 | 16.1 | 0.863 | 0.678 | 1.410 4 |
| Litsea variabilis | Exponential model | 1.285 | 3.567 | 0.360 | 0.640 | 8.9 | 0.148 | 0.876 | 1.392 1 |
| Ardisia quinquegona | Linear model | 1.278 | 1.521 | 0.840 | 0.160 | 38.3 | 0.469 | 0.141 | 1.297 1 |
| Psychotria asiatica | Linear model | 0.876 | 0.977 | 0.897 | 0.103 | 38.2 | 0.009 | 0.627 | 1.260 1 |
| 种名 Species name |
鹅掌柴 Heptapleurum heptaphyllum |
肉实树 Sarcosperma laurinum |
银柴 Aporosa dioica |
黄椿木姜子 Litsea variabilis |
罗伞树 Ardisia quinquegona |
| Sarcosperma laurinum | -3.23* | ||||
| Aporosa dioica | -0.73 | 2.50* | |||
| Litsea variabilis | 1.99* | 5.22* | 2.72* | ||
| Ardisia quinquegona | 2.00* | 5.23* | 2.73* | 0.01 | |
| Psychotria asiatica | 2.40* | 5.63* | 3.13* | 0.41* | 0.40* |
| Note:*indicates a significant level of 0.05. | |||||
| 种名 Species name |
鹅掌柴 Heptapleurum heptaphyllum |
肉实树 Sarcosperma laurinum |
银柴 Aporosa dioica |
黄椿木姜子 Litsea variabilis |
罗伞树 Ardisia quinquegona |
| Sarcosperma laurinum | -0.65* | ||||
| Aporosa dioica | 0.95* | 1.60* | |||
| Litsea variabilis | 3.53* | 4.18* | 2.58* | ||
| Ardisia quinquegona | 5.58* | 6.23* | 4.63* | 2.05* | |
| Psychotria asiatica | 6.22* | 6.88* | 5.27* | 2.69* | 0.65* |
| Note:*indicates a significant level of 0.05. | |||||
2.2 株高空间异质性组成
空间异质性由随机部分和自相关部分组成[3-5],两者的重要程度可用块金值与基台值之比即块金系数来度量,该比值越高,说明由随机因素引起的空间异质性程度越高。由表 1可知,本研究区域内鹅掌柴、肉实树、银柴、黄椿木姜子、罗伞树和九节6个主要树种株高由随机因素引起的空间异质性占总空间异质性的百分比(块金系数)分别为46.2%、83.9%、65.2%、36.0%、84.0%和89.7%,呈九节>罗伞树>肉实树>银柴>鹅掌柴>黄椿木姜子;而由自相关因素引起的空间异质性占总空间异质性的百分比,即结构方差比,分别为53.8%、16.1%、34.8%、64.0%、16.0%和10.3%,呈黄椿木姜子>鹅掌柴>银柴>肉实树>罗伞树>九节。t-检验表明,除鹅掌柴-黄椿木姜子、肉实树-罗伞树、肉实树-九节、罗伞树-九节4个种对之外,其他11个种对间的块金系数均呈显著性差异(表 4)。
| 种名 Species name |
鹅掌柴 Heptapleurum heptaphyllum |
肉实树 Sarcosperma laurinum |
银柴 Aporosa dioica |
黄椿木姜子 Litsea variabilis |
罗伞树 Ardisia quinquegona |
| Sarcosperma laurinum | -0.38* | ||||
| Aporosa dioica | -0.19* | 0.19* | |||
| Litsea variabilis | 0.10 | 0.48* | 0.29* | ||
| Ardisia quinquegona | -0.38* | -0.00 | -0.19* | -0.48* | |
| Psychotria asiatica | -0.44* | -0.06 | -0.25* | -0.54* | -0.06 |
| Note:*indicates a significant level of 0.05. | |||||
2.3 株高空间异质性尺度
空间异质性是尺度的函数[18]。由表 1和图 1可知,鹅掌柴、肉实树、银柴、黄椿木姜子、罗伞树、九节6个树种株高的变程明显不同,最小为8.9 m,最大为38.3 m,呈罗伞树>九节>银柴>肉实树>鹅掌柴>黄椿木姜子。t-检验表明,鹅掌柴-肉实树、鹅掌柴-银柴、肉实树-银柴、肉实树-黄椿木姜子、罗伞树-九节5个种对的变程差异不显著,而其他10个种对间差异显著(表 5)。
| 种名 Species name |
鹅掌柴 Heptapleurum heptaphyllum |
肉实树 Sarcosperma laurinum |
银柴 Aporosa dioica |
黄椿木姜子 Litsea variabilis |
罗伞树 Ardisia quinquegona |
| Sarcosperma laurinum | -1.86 | ||||
| Aporosa dioica | -3.31 | -1.45 | |||
| Litsea variabilis | 3.91* | 5.77 | 7.22* | ||
| Ardisia quinquegona | -25.46* | -23.60* | -22.15* | -29.37* | |
| Psychotria asiatica | -35.38* | -23.52* | -22.07* | -29.29* | 0.08 |
| Note:*indicates a significant level of 0.05. | |||||
2.4 株高空间格局
植物种群的空间格局主要受其自身的生物学特性和生境异质性的影响[6-13]。通过Kriging插值法绘制得到的空间格局图,不仅可以直观地反映种群空间格局的特征,而且还可以对其潜在分布进行模拟和预测。图 2显示,鹅掌柴、肉实树、银柴、黄椿木姜子、罗伞树、九节6个主要树种株高在水平空间上均呈明显斑块状分布,但不同树种的斑块大小、斑块数量及其镶嵌复杂程度均有所不同,说明它们在同一群落中的空间格局存在明显的差异。

|
| 图 2 鹅掌柴群落主要树种株高的空间格局 Fig.2 Spatial patterns of plant heights of main tree species in H.heptaphyllum community |
3 讨论 3.1 株高空间异质性及其成因
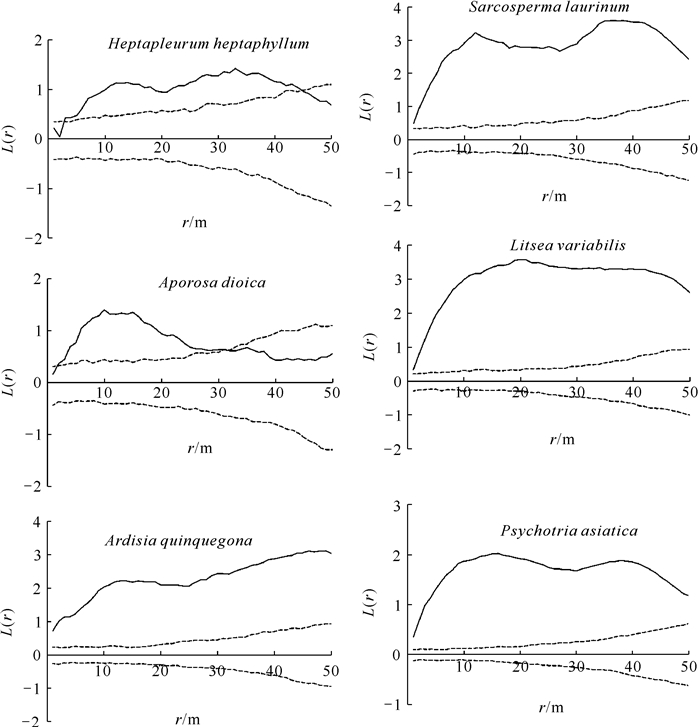
半方差函数曲线和Kriging插值法是地统计学理论的主要内容[2-5]。半方差函数曲线的基本参数包括块金值、基台值、变程等。块金值为随机部分的空间异质性,较大的块金值表明较小尺度上的某种过程不可忽视,因此要了解种群微域结构特征必须进行小尺度取样[4]。块金系数可揭示变量的空间相关程度,若块金系数 < 25%,表示变量空间自相关性强,空间变异主要受自相关因素影响;若块金系数为25%-75%,表示变量空间自相关性中等,空间变异是自相关因素和随机因素共同作用的结果;若块金系数>75%,表示变量空间自相关性弱,空间变异主要受随机因素影响。在鹅掌柴群落中,6个主要树种株高的块金系数明显不同,说明不同树种株高空间异质性的成因有所差异。鹅掌柴、银柴和黄椿木姜子株高的块金系数为25%-75%,这些树种株高的空间异质性由自相关因素和随机因素共同作用引起。其中,鹅掌柴株高的块金系数为46.2%,空间异质性的两部分组成比例接近,说明自相关因素和随机因素都起重要作用;银柴株高的块金系数为65.2%,说明随机因素对其空间异质性的作用较大;黄椿木姜子株高的块金系数为36.0%,说明自相关因素引起的空间异质性起决定作用,但随机部分引起的空间异质性不能忽视。上述结果与陈科屹等[6]、丁杰等[7]、王猛等[8]、叶尔江·拜克吐尔汉等[9]的研究结果类似。肉实树、罗伞树和九节株高的块金系数大于75%,说明由随机因素引起的空间异质性起决定作用,这些树种在小尺度上具有重要的生态学过程,并可能与物种的繁殖特性有关。肉实树为总状花序或圆锥花序,核果长1.5-2.5 cm;罗伞树和九节为聚伞花序,核果长不足1 cm。这3个树种不仅种子数量多而且主要散布在母树树冠下或其周围,因此群落内的小生境对这些树种的种子萌发及自然更新影响较大。变程为半方差函数达到基台值时的点对间距,是度量空间异质性尺度的有效参数,它反映空间自相关范围的大小,即在有效变程内,变量具有空间自相关特性,反之则不存在空间自相关特性[2-5]。植物种群的空间分布格局和自相关性反映了种群个体在空间上的配置状况和彼此间的相互联系,因此确定和检验种群的空间自相关尺度,有助于认识与尺度所对应的种群空间格局和动态过程的差异。根据图 3,鹅掌柴除3 m以下和45 m以上的尺度呈随机分布外,其余尺度都呈集群分布。银柴在31 m以下尺度呈集群分布,31 m以上尺度呈随机分布;而肉实树、黄椿木姜子、罗伞树和九节在所有尺度上都呈集群分布。图 2也显示,这些树种株高在水平空间上呈明显的斑块状分布,但不同树种株高的斑块大小、数量及其镶嵌复杂程度有所不同,即它们在同一群落中的空间异质性存在较大的差异,说明不同树种株高的空间格局特征及其成因不尽相同。野外调查发现,1 hm2群落样地有维管植物65科127属178种,这意味着种间竞争趋势较强;群落内出现的岩石露头和冲沟增加了生境异质性,这些也是树种株高空间异质性形成的重要因素。
|
——: L(r), Ripley′s L function;  : 99% confidence interval; r: sampling scale.
图 3 鹅掌柴群落主要树种株高的点格局分析
Fig.3 Point pattern analysis of plant heights of main tree species in H.heptaphyllum community : 99% confidence interval; r: sampling scale.
图 3 鹅掌柴群落主要树种株高的点格局分析
Fig.3 Point pattern analysis of plant heights of main tree species in H.heptaphyllum community
|
3.2 株高空间异质性与其占据空间能力的关系
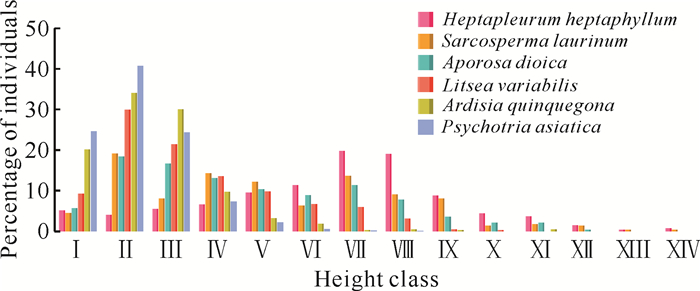
植物种群空间异质性与其生物学特性,特别是占据空间的能力密切相关。根据图 4,在鹅掌柴群落中,鹅掌柴为常绿乔木,是群落的建群种,种群密度为274株·hm-2,高度结构呈壶型,以Ⅶ和Ⅷ级个体较多,两者占种群个体总数的38.69%。肉实树为常绿乔木,为群落乔木层第Ⅱ或Ⅲ亚层的优势种,种群密度为288株·hm-2,高度结构呈金字塔形,以Ⅱ级个体较多,占种群个体总数的19.10%;其次是Ⅳ、Ⅴ和Ⅶ级个体,分别占14.24%、12.15%和13.54%。银柴为常绿乔木,为群落乔木层第Ⅱ或Ⅲ亚层的优势种,种群密度为283株·hm-2,高度结构呈金字塔形,以Ⅱ和Ⅲ级个体较多,两者占种群个体总数的34.98%。黄椿木姜子为常绿灌木或乔木,为群落乔木层第Ⅲ亚层和灌木层的优势种,种群密度为422株·hm-2,高度结构呈金字塔形,以Ⅱ和Ⅲ级个体较多,两者占种群个体总数的51.18%。罗伞树为常绿灌木或灌木状小乔木,是灌木层的优势种,种群密度为444株·hm-2,高度结构呈金字塔形,以Ⅱ和Ⅲ级个体较多,两者占种群个体总数的63.96%。九节为常绿灌木或小乔木,是灌木层的优势种,种群密度为977株·hm-2,高度结构呈金字塔形,以Ⅱ级个体较多,占种群个体总数的40.74%;其次是Ⅰ和Ⅲ级个体,分别占24.56%和24.36%,三者占89.66%。由此可见,在群落垂直空间上,6个主要树种在不同高度级上占据优势。根据图 2,在群落水平空间上,鹅掌柴、肉实树、银柴和黄椿木姜子株高的斑块大小、数量及其镶嵌程度相对复杂,而罗伞树和九节的相对简单。种群空间格局的复杂程度及其占据空间的能力,可用分形维数来定量表征,分形维数值越大,表明种群对空间环境的占据利用能力越强,个体空间聚集程度越强,在群落中处于优势地位;反之,则表明其对空间环境的占据利用能力弱,个体聚集程度越低,处于伴生地位[19, 20]。根据表 1,6个主要树种空间格局分形维数的大小顺序为鹅掌柴(1.429 6)>肉实树(1.411 6)>银柴(1.410 4)>黄椿木姜子(1.392 1)>罗伞树(1.297 1)>九节(1.260 1),说明乔木种群的空间异质性及占据空间能力比灌木种群的高;同时,种群聚集程度越强,其空间格局非均匀性越高,这一结果与张忠华等[20]的结果类似。种群通过竞争、生态位分异和耐性幅度占据各自适生的空间,以充分利用群落的生态空间。
|
| 图 4 鹅掌柴群落主要树种的高度结构 Fig.4 Height structure of main tree species in H.heptaphyllum community |
4 结论
本研究采用地统计学理论和方法研究防城季节性雨林组成树种空间异质性的特点及其驱动因素构成,结果表明防城季节性雨林鹅掌柴、肉实树、银柴、黄椿木姜子、罗伞树和九节6个树种株高空间异质性的程度、尺度和格局存在明显差异,这是树种生物生态学特性、种间竞争、生境异质性等因素共同作用的结果。
| [1] |
陈玉福, 董鸣. 生态学系统的空间异质性[J]. 生态学报, 2003, 23(2): 346-352. DOI:10.3321/j.issn:1000-0933.2003.02.019 |
| [2] |
ROSSI R E, MULLA D J, JOUREL A G, et al. Geostatistical tools for modeling and interpreting ecological spatial dependence[J]. Ecological Monographs, 1992, 62(2): 277-314. DOI:10.2307/2937096 |
| [3] |
MATHERON G. Principles of geostatistics[J]. Economic Geology, 1963, 58(8): 1246-1266. DOI:10.2113/gsecongeo.58.8.1246 |
| [4] |
王政权. 地统计学及在生态学中的应用[M]. 北京: 科学出版社, 1999.
|
| [5] |
ROBERTSON G P. Geostatistics in ecology: interpolating with known variance[J]. Ecology, 1987, 68(3): 744-748. DOI:10.2307/1938482 |
| [6] |
陈科屹, 张会儒, 雷相东. 不同群落蒙古栎种群空间格局的地统计学分析[J]. 应用生态学报, 2018, 29(5): 1542-1550. |
| [7] |
丁杰, 张谱, 张和钰, 等. 天山南麓中段戈壁区膜果麻黄种群空间分异特征[J]. 应用生态学报, 2020, 31(12): 3997-4003. |
| [8] |
王猛, 汪季, 蒙仲举, 等. 巴丹吉林沙漠东缘天然梭梭种群空间分布异质性[J]. 生态学报, 2016, 36(13): 4055-4063. |
| [9] |
叶尔江·拜克吐尔汉, 李海燕, 朱小虎, 等. 北疆荒漠优势灌木种群空间异质性分析[J]. 干旱区资源与环境, 2014, 28(8): 71-76. |
| [10] |
庞洁, 和太平, 黎向东, 等. 防城金花茶国家级自然保护区植物群落的聚类分析[J]. 广西科学院学报, 2008, 24(3): 189-193. DOI:10.3969/j.issn.1002-7378.2008.03.010 |
| [11] |
向悟生, 王斌, 李先琨, 等. 广西防城季节性雨林物种及其分布格局[M]. 北京: 中国林业出版社, 2021.
|
| [12] |
吴林芳, 李维标, 李珊珊, 等. 防城金花茶国家级自然保护区次生季雨林木本植物多样性与种间联结性[J]. 湖南林业科技, 2022, 49(1): 7-13. |
| [13] |
廖南燕, 陈善栋, 李武峥, 等. 防城金花茶国家级自然保护区罗浮柿种群空间分布格局及关联分析[J]. 安徽农业科学, 2024, 52(1): 121-124. |
| [14] |
ROBERTSON G P. Geostatistics for the environmental sciences[M]. Version 10. Plainwell, Michigan USA: Gamma Design Software, 2008.
|
| [15] |
RIPLEY B D. Modelling spatial patterns[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1977, 39(2): 172-192. |
| [16] |
DRAY S, DUFOUR A B. The ade4 package: implementing the duality diagram for ecologists[J]. Journal of Statistical Software, 2007, 22(4): 1-20. |
| [17] |
SCHNEIDER C A, RASBAND W S, ELICEIRI K W. NIH image to ImageJ: 25 years of image analysis[J]. Nature Methods, 2012, 9(7): 671-675. |
| [18] |
LI H, REYNOLDS J F. On definition and quantification of heterogeneity[J]. Oikos, 1995, 73(2): 280-284. |
| [19] |
梁士楚. 云贵鹅耳枥种群分布格局的分形特征[J]. 武汉植物学研究, 2001, 19(4): 263-268. |
| [20] |
张忠华, 胡刚, 倪健. 茂兰喀斯特常绿落叶阔叶混交林树种的空间分布格局及其分形特征[J]. 生态学报, 2015, 35(24): 8221-8230. |


