2. 冶金工业过程系统科学湖北省重点实验室(武汉科技大学), 湖北武汉 430081
2. Hubei Province Key Laboratory of Systems Science in Metallurgical Process (Wuhan University of Science and Technology), Wuhan, Hubei, 430081, China
随着国家弘扬传统文化力度的不断加大,京剧逐渐进入大众视野,但其在大众,特别是青年群体中尚未能有效推广[1, 2]。在京剧并不流行的时代,人们很难区分京剧与其他类型的音乐。因此,京剧与其他类型音乐的二分类(以下简称“京剧二分类”)问题的研究就显得十分必要。
近年来,虽然对京剧音频研究较少,但对各种音乐、语音以及自然声音的研究层出不穷。Saunders[3]和Scheirer等[4]使用短时能量、过零率等频谱特征直接对语音与音乐进行二分类;Lim等[5]在支持向量机(SVM)分类器的基础上通过改进分类器等方式改进原始音乐分类方法,降低了计算成本并提高了准确率。考虑到音乐的频谱信息是音乐本质的体现,复杂的音频或许不能被少数的几种频谱信息完全翻译,Birajdar等[6, 7]通过音频产生的色谱图、光谱图以及其统计描述符保留语音与音乐的纹理后进行二分类,但利用谱图与音乐纹理进行分类增加了分类难度;姚斯强等[8]和万凌艳[9]提取高维频谱特征后,利用线性判别分析(LDA)、核主成分分析法对特征降维,而后利用SVM等分类方法进行训练,证实对原始音频特征降维后再利用分类器训练能有效提高分类准确率,但通过线性降维的方式所得到的特征并不是原始特征的子集,故该方式缺乏挑选重要特征的能力。
除了利用传统的音频特征进行音频分类外,也有许多学者考虑到音频的时间序列特性与情感特性,将各种神经网络用于音频研究中。Tu等[10]和Zhang等[11]利用循环神经网络(RNN)的特殊结构与时间学习能力,弥补短期特征的不足并提高对音频长度处理的灵活性,提高模型对混合音频的分类准确率,但RNN模型在处理较长时间序列时容易产生梯度消失与梯度爆炸问题,影响分类准确率;郭毓博等[12]将长短时记忆(LSTM)网络应用于笛音分类中,通过多种模型的混合比较得出最佳分类模型;Yu等[13]在音频特征提取的基础上引入注意力(Attention)机制增强特定频段,以此提高音频分类准确率,但该方法仅考虑特定频段,缺乏对局部时间信息与全局时间信息的联系。Noumida等[14]将注意力机制与双向门控循环单元模型结合来对鸟类声音分类,该方法能够提高分类性能,但在一定程度上缺乏对音频信号为强时间序列的考虑。
综上所述,本研究提出一种基于RF-BiLSTM-Attention的音乐分类方法,将具有特征筛选能力的随机森林(Random Forest, RF)和能够双向学习时间序列的双向长短时记忆(BiLSTM)模型结合,再利用注意力机制抓取音频的全局信息。通过实验对比分析,验证所提出的方法在京剧二分类问题上的可行性,为后续国粹京剧推广相关工作提供研究基础。
1 BiLSTM网络及其基础网络BiLSTM网络适用于具有前后时间联系的音频数据,由一个前向LSTM网络与一个后向LSTM网络构成[15],改善了LSTM网络仅能单向学习时间信息的问题。LSTM网络由RNN改变隐藏层结构所得,能够有效缓解RNN在梯度更新过程中造成的梯度消失与梯度爆炸问题。
1.1 RNNRNN广泛应用于序列数据,独特的链式结构使其增加了对信息的记忆功能。其结构如图 1所示。

|
| 图 1 RNN基本结构 Fig.1 Basic structure of RNN |
由图 1可见,RNN包含输入层X、隐藏层S以及输出层O,在隐藏层实现循环。隐藏层状态与输出计算公式如式(1)、(2)所示。
| $ S_t=\phi\left(U \cdot X_t+W \cdot S_{t-1}+b_s\right), $ | (1) |
| $ O_t=V \cdot S_t+b_o \text {, } $ | (2) |
式(1)、(2)中,St、Ot分别表示t时刻的隐藏层与输出层状态,ϕ为激活函数,bs、bo分别为隐藏层与输出层偏置,W、U、V分别为隐藏层、输入层、输出层的权值矩阵。通常运用梯度下降对权值矩阵参数W、U、V更新,更新公式如式(3)-(5)所示。
| $ \begin{aligned} & \ \ \ \ \ \ \ W=W-\operatorname{lr} \sum\limits_{i=0}^t \frac{\partial e_t}{\partial W}=W-\operatorname{lr} \sum\limits_{i=0}^t \frac{\partial e_t}{\partial O_t} \frac{\partial O_t}{\partial S_t} \frac{\partial S_t}{\partial S_i} \\ & \frac{\partial S_i}{\partial W}, \ \ \ \ \ \end{aligned} $ | (3) |
| $ U=U-\operatorname{lr} \sum\limits_{i=0}^t \frac{\partial e_t}{\partial U}=U-\operatorname{lr} \sum\limits_{i=0}^t \frac{\partial e_t}{\partial O_t} \frac{\partial O_t}{\partial S_t} \frac{\partial S_t}{\partial S_i} \frac{\partial S_i}{\partial U}, $ | (4) |
| $ V=V-\operatorname{lr} \sum\limits_{i=0}^t \frac{\partial e_t}{\partial V}=V-\operatorname{lr} \sum\limits_{i=0}^t \frac{\partial e_t}{\partial O_t} \frac{\partial O_t}{\partial S_t} \frac{\partial S_t}{\partial S_i} \frac{\partial S_i}{\partial V}, $ | (5) |
式(3)-(5)中,et为每次输出值Ot与真实值之间的误差,lr为学习率Learn rate的缩写, Si为i时刻隐藏层状态。
由式(3)-(5)可看出,在递归计算梯度过程中,如果权值矩阵的值小于1,那么梯度则会逐渐趋于0,造成梯度消失;如果权值矩阵的值大于1,梯度则会趋于无穷,造成梯度爆炸。
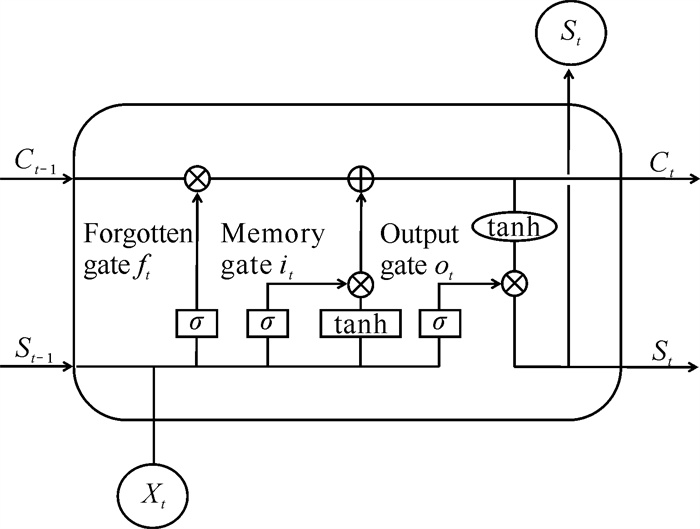
1.2 LSTM网络LSTM网络是一种特殊的RNN,其在原本的RNN隐藏层结构基础上增加了遗忘门、记忆门、输出门3个门控装置以及细胞状态,有效解决了RNN可能带来的梯度消失与梯度爆炸问题[16]。RNN、LSTM网络隐藏层结构分别如图 2、图 3所示。

|
| 图 2 RNN隐藏层基本结构 Fig.2 Basic structure of RNN hidden layer |
|
| 图 3 LSTM网络隐藏层基本结构 Fig.3 Basic structure of LSTM network hidden layer |
由图 3可见,t时刻的输入为Xt,细胞状态为Ct,隐层状态为St,遗忘门为ft,记忆门为it,输出门为ot。其中细胞状态用于保存先前节点信息,隐层状态为当前输入提供门控信号,3个门用于遗忘细胞中的原始信息与记忆新信息。具体计算公式如式(6)-(11)所示。
| $ \widetilde{C}_t=\tanh \left(W_{X C} X_t+W_{S c} S_{t-1}+b_c\right), $ | (6) |
| $ C_t=f_t C_{t-1}+i_t \widetilde{C}_t, $ | (7) |
| $ f_t=\sigma\left(W_{X f} X_t+W_{S f} S_{t-1}+W_{C f} C_{t-1}+b_f\right), $ | (8) |
| $ i_t=\sigma\left(W_{X i} X_t+W_{S i} S_{t-1}+W_{C i} C_{t-1}+b_i\right) \text {, } $ | (9) |
| $ o_t=\sigma\left(W_{X_o} X_t+W_{S_o} S_{t-1}+W_{C_o} C_{t-1}+b_o\right), $ | (10) |
| $ S_t=o_t \tanh \left(C_t\right), $ | (11) |
式(6)-(11)中,
| $ \begin{aligned} & \ \ \ \ \ \quad \frac{\partial C_t}{\partial C_{t-1}}=\frac{\partial C_t}{\partial f_t} \frac{\partial f_t}{\partial S_{t-1}} \frac{\partial S_{t-1}}{\partial C_{t-1}}+\frac{\partial C_t}{\partial i_t} \frac{\partial i_t}{\partial S_{t-1}} \frac{\partial S_{t-1}}{\partial C_{t-1}}+ \\ & \frac{\partial C_t}{\partial \widetilde{C}_{t-1}} \frac{\partial \widetilde{C}_{t-1}}{\partial S_{t-1}} \frac{\partial S_{t-1}}{\partial C_{t-1}}+\frac{\partial C_t}{\partial C_{t-1}} 。\end{aligned} $ | (12) |
在RNN的梯度更新过程中,
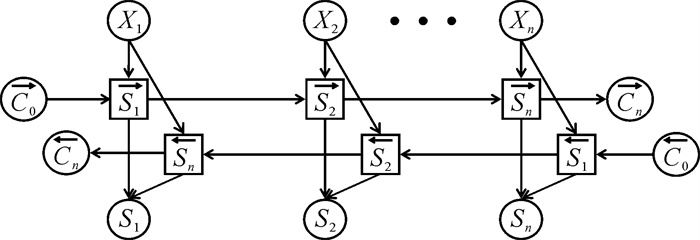
BiLSTM网络由两个反向传播的LSTM网络构成,结构如图 4所示。由图 4可见,t时刻的输入Xt同时进入前向传播的LSTM网络与后向传播的LSTM网络,因此其可以同时学习t-1、t+1两个时刻的信息,并综合输出t时刻隐层状态。
|
| 图 4 双向长短时记忆网络传播过程 Fig.4 Propagation process of bidirectional long short-term memory network |
对于具有强前后联系的音频时间序列,选用BiLSTM网络可以同时学习某时刻前、后两方向的信息,加强信息学习能力以提高分类准确率。但BiLSTM网络本质还是一个长短时记忆网络,仍缺乏对时间序列全局信息的学习能力,并且在学习某时步信息时,太过于依赖前一时刻的计算结果。
2 基于RF-BiLSTM-Attention的音乐分类模型音乐频谱特征是音乐本质的体现,但音频特征维度过大不利于后续模型训练,因此提取全部光谱特征后,采用能够保留原始音频信息的非线性降维方式RF进行特征挑选。使用BiLSTM网络对具有强时间序列的音频文件进行训练,能够获取局部时间信息,但其在长时间序列上仍会产生信息损失,并且计算过程中过于依赖序列前后关系。因此本研究提出在BiLSTM网络上融入注意力机制,以期增强模型长时间序列学习能力并减少计算时间。
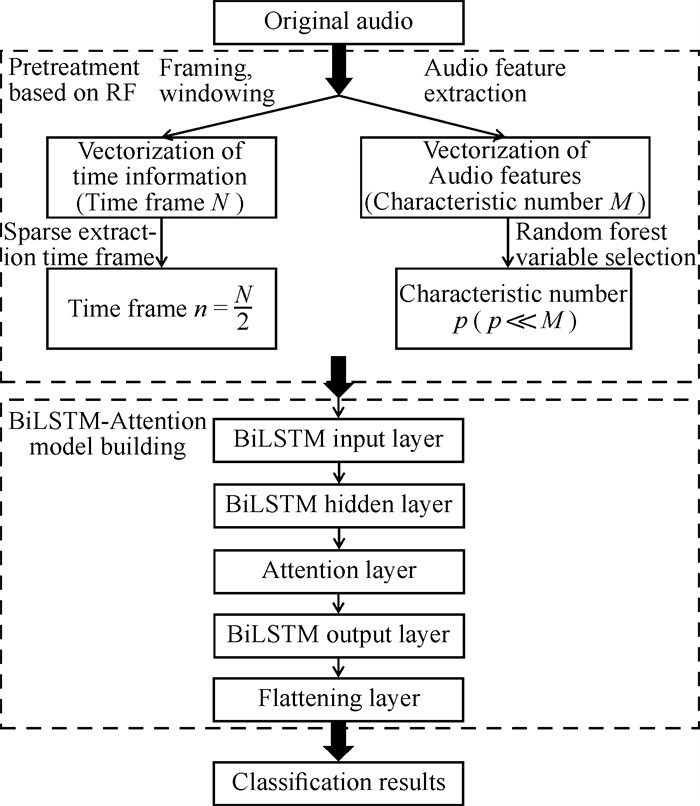
2.1 基于RF-BiLSTM-Attention的模型框架基于RF-BiLSTM-Attention的模型包括基于RF的数据预处理和BiLSTM-Attention模型构建两个部分,模型框架如图 5所示。为在不增加训练难度的基础上获取最重要的频谱特征,首先提取所有光谱特征;然后利用RF对特征重要性打分,挑选重要特征进行分类训练。为增强模型对于音频时间序列前后逻辑以及全局关联的学习,先以适用于时间序列的BiLSTM网络为基础模型学习音频局部信息;之后通过在其隐藏层与输出层之间嵌入注意力层,给每个时间帧赋予不同权重,同时学习音频全局信息并使其聚焦于更能反应音乐类型的时间帧,提高分类准确率。其中在BiLSTM网络中嵌入注意力机制是核心内容,其融合过程也是研究难点。
|
| 图 5 RF-BiLSTM-Attention模型框架 Fig.5 Model framework of RF-BiLSTM-Attention |
2.2 基于RF的数据预处理
数据预处理是将原本的音频文件转换为包含时间信息与光谱特征信息的向量,并尽量压缩其维度为分类模型训练降低难度。该过程包括音频矩阵生成和RF变量选择两个步骤。
2.2.1 音频矩阵生成音乐信号属于人体语音的一种,要将其转化为分类训练需要的特征,首先对原始音频进行分帧、加窗、傅里叶变换、反傅里叶变换等操作才能获得对应的信号特征。对于给定音乐S,经过分帧、加窗等,将其划分为N个时间帧,对应的时间向量记为S(t1, t2, …, ti, …, tN);再通过傅里叶变换、反傅里叶变换等操作获得所有光谱特征M个,特征向量记为S(a1, a2, …, ai, …, aM)。将特征向量与时间向量组合生成一个M行N列的初始音频矩阵。
一般音频对应的时间与特征都具有较高维度,但高维数据会使得训练难度加大,时间加长。因此,利用稀疏抽取时间帧的方式,即抽取原始时间帧奇数或偶数的时间帧,将原始时间帧N降至n=N/2帧,使得时间帧维度降为原来的一半,再利用RF对所有特征重要性打分并选择重要特征,实现特征降维。
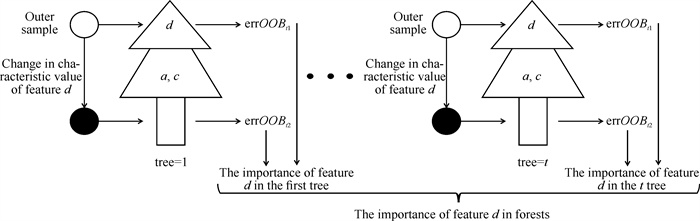
2.2.2 RF变量选择Breiman[17]在2001年首次提出RF模型,其是一种非线性的降维方式,可以保留原始特征信息。该模型用于特征选择时可以高效地给出特征的重要性得分[18]。通常使用袋外误差,即特征值改变前后的测试集误差率衡量特征的重要程度。特征重要性得分计算过程如图 6所示。其中a、c、d为特征变量。
|
| 图 6 特征d的重要性得分计算流程 Fig.6 Importance score calculation process for feature d |
根据图 6,特征重要性得分计算有以下流程:①在M个光谱特征中随机抽取H个特征构建G棵决策树,再随机选择决策树g,其中g由D个特征构成,随机选择特征Gd,计算测试集(为M中未被抽取的部分)误差率errOOBt1;②改变特征d的特征值后再次计算测试集误差率errOOBt2,测试集前、后误差率差值为特征Gd在决策树g中的重要程度;③遍历G棵树中的特征值d,计算其重要程度的平均值(MDA),用该平均值来衡量该特征在森林中的重要程度,计算公式如式(13)所示:
| $ \operatorname{MDA}(d)=\frac{1}{G_d \text { tree }} \sum\limits_{t=1}^{G_d \text { tree }}\left(\operatorname{err} O O B_{t 1}-\operatorname{err} O O B_{t 2}\right), $ | (13) |
其中,Gd tree为特征d在森林中出现的次数,errOOBt1为特征d的值改变前的测试集误差率,errOOBt2为特征d的值改变后的测试集误差率。
根据上述步骤计算出所有特征的重要性得分并排序,再选取合适阈值或者所需要的特征个数,从M个特征中选取m个重要特征。基于RF预处理后得到一个m行n列的音频矩阵,将其作为后续所有模型的输入矩阵进行训练与预测。
2.3 BiLSTM-Attention模型构建使用BiLSTM对音频进行分类,可以加强模型对音频序列前后关系的学习能力。在此基础上融入注意力机制可加强全局时间的联系,并突出特定时间帧对于音乐分类的重要程度。
2.3.1 BiLSTM-Attention模型流程音乐S经过数据预处理后得到一个m×n的二维矩阵,将其作为BiLSTM-Attention模型的输入进行训练,BiLSTM-Attention模型训练具体流程如图 7所示。音乐S产生的m×n的二维矩阵进入BiLSTM网络输入层后按时间展开为n个时间步,其中每个时间步包含m个特征,音乐S第i个时间步的向量记为Xi=(aS1, aS2, …, aSm)Ti。输入数据进入BiLSTM隐藏层进行训练,学习局部时间信息后从隐藏层输出新向量Xi′=(aS1′, aS2′, …, aSm′)Ti,将其直接输入注意力机制层,计算每个时间帧的注意力得分bi,为每个时间帧赋予权值,将每帧的权值与经过BiLSTM网络学习所得到的信息相结合,得到最终学习结果Xi″=(aS1″, aS2″, …, aSm″)Ti。再组合n个时间帧的信息,得到BiLSTM-Attention模型的输出,进入展平层以及分类器输出最终分类结果。
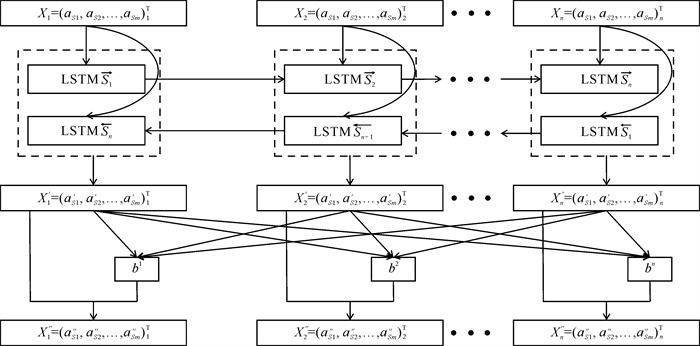
|
| 图 7 BiLSTM-Attention模型流程框架 Fig.7 Process framework of BiLSTM-Attention model |
2.3.2 注意力机制计算原理
注意力机制在学习某时间步信息时,同时考虑所有时间步产生的影响,并且不依赖前后时间步计算出的信息[19],弥补了原始BiLSTM网络在学习过程中无法考虑全局带来的信息损失,解决了依赖前个时间步计算结果造成的运算速度慢的问题。
注意力机制中每个输入都会引申出3个向量:q、k、v,其中q为查询向量query,k为键向量keys,v为值向量value。通过3个向量与输入的计算,得出最终的注意力得分。第i个时间步的注意力得分bi计算过程如图 8所示。

|
| 图 8 时间步i的注意力得分计算流程 Fig.8 Attention score calculation process of time step i |
图 8中,qi、ki、vi和α′i, j、bi分别为对应时间步的q、k、v向量和注意力权值、注意力得分。计算公式如式(14)所示:
| $ \begin{aligned} & \ \ \ \ \ \ \ q^i=W^q \cdot X_i ; k^i=W^k \cdot X_i ; v^i=W^v \cdot X_i ; \alpha_{i, j}^{\prime}= \\ & \operatorname{softmax}\left(q^i k^j\right) ; b^i=\sum\limits_j \alpha_{i, j}^{\prime} v^i, \end{aligned} $ | (14) |
其中,Wq、Wk、Wv为对应的权值矩阵。
经过BiLSTM网络隐藏层学习后得到X1′,X2′,…,Xn′,计算得到每个时间步所对应的q、k、v向量,将第i个时间步对应的q向量分别与自身以及其他时间步对应的k向量相乘,得到每个时间步对应的权值αi, j,再通过软最大化函数softmax进行转化得到权值αi, j′,最后将其与对应时间步的v向量相乘再相加得到第i个时间步的注意力得分bi。通过以上步骤,计算出每个时间步对应的注意力得分,实现BiLSTM-Attention模型中注意力机制的嵌入。
3 实验结果与分析基于上述模型框架,将RF-BiLSTM-Attention模型、BiLSTM-Attention模型分别与RNN、LSTM、BiLSTM等9种模型进行京剧二分类实验及对比实验。
3.1 实验数据集选取来源于大众音乐平台的京剧和5种戏曲,以及GTZAN数据集上提供的10种音乐流派歌曲,共计1 500首歌曲进行实验。采样歌曲类型及数量见表 1。
| 音乐流派 Music genre |
数量 Number |
合计 Total |
| Beijing Opera | 750 | 750 |
| Other Ping Opera | 50 | 750 |
| Huangmei Opera | 50 | |
| Henan Opera | 50 | |
| Shaanxi Opera | 50 | |
| Shaoxing Opera | 50 | |
| GTZAN dataset 10 music genres (50 songs selected for each genre) | 500 |
如表 1所示,本研究选取京剧与其他类型音乐各750首,保证了数据集的平衡性;且其他音乐类型中包含戏曲和流行音乐,增加了数据集的丰富度,加大了分类可信度。将上述两类音频文件对应进行独立热编码,“京剧”标签为0,“其他”标签为1。
3.2 模型评价指标在分类问题中,准确率是衡量模型分类好坏标准最常见的指标,它能够直接反映正确分类的比例。由于本研究为二分类问题,因此采取混淆矩阵定义的准确率对京剧二分类模型分类好坏进行评判。混淆矩阵由真实值Positive (TP)、Negative (TN)以及模型认为的Positive (FP)、Negative (FN) 4个值所组成,可计算准确率(Accuracy),计算公式如式(15)所示:
| $ \text { Accuracy }=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}。$ | (15) |
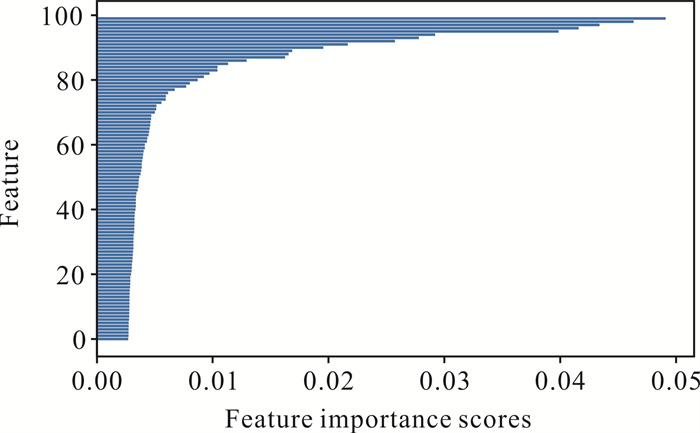
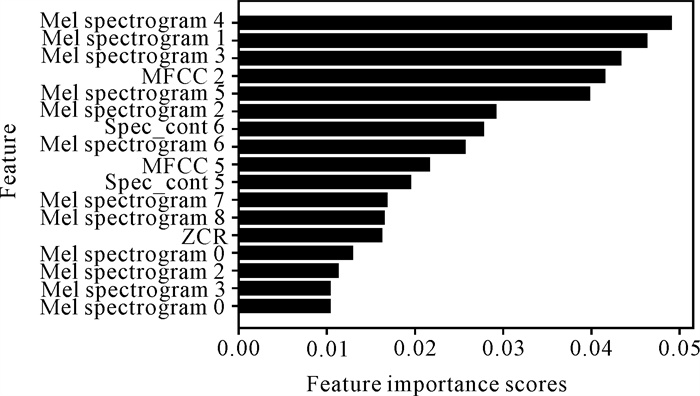
截取原始音频文件中每首歌曲的前10 s,并划分为431个时间帧。每个时间帧抽取14大类共计205维光谱特征。经过稀疏抽取时间帧与RF降维后,得到的后续模型输入矩阵为216行、17列。其中通过RF所给出的特征重要性得分如图 9所示,降维后的特征如图 10所示。
|
| 图 9 前100个特征重要性得分 Fig.9 Top 100 feature importance scores |
|
| 图 10 重要性得分大于0.01的特征变量 Fig.10 Feature variables with importance scores greater than 0.01 |
从图 9可以看出,特征重要性得分小于0.01的特征占总特征的85%,且该部分特征的重要性得分差别不大,因此选取0.01作为特征筛选的阈值。由于梅尔频谱特征共128维,能够提供丰富的频域信息与时域变化,且涵盖声音特性信息,因此图 10中筛选出的17维特征中71%为梅尔频谱特征。
3.4 实验结果与分析将数据划分为训练验证集和测试集,其中训练验证集包含1 200首歌曲,测试集包含300首。将训练验证集作为模型的输入进行训练,再使用测试集对训练后的模型进行测试和评估。为更好地说明本研究所提出的RF-BiLSTM-Attention模型对于分类效果的准确率以及训练时间上的优势,将该模型与RNN、LSTM、BiLSTM、BiLSTM-Attention等9种模型进行比较,并分别使用未经过RF处理的数据与经过RF处理的数据进行对比实验,实验结果如表 2、表 3所示。
| 神经网络模型 Neural network model |
准确率/% Accuracy/% |
运行时间/s Run time/s |
|
| Simple model | CNN | 83.67 | 185.67 |
| Attention | 71.00 | 170.00 | |
| GRU | 85.00 | 505.05 | |
| BiGRU | 86.00 | 788.45 | |
| RNN | 78.00 | 243.10 | |
| LSTM | 83.30 | 534.04 | |
| BiLSTM | 86.33 | 807.13 | |
| Complex model | CNN+LSTM | 74.00 | 158.52 |
| BiGRU+Attention | 77.00 | 570.44 | |
| BiLSTM-Attention | 82.67 | 1 035.88 | |
| 神经网络模型 Neural network model |
准确率/% Accuracy/% |
运行时间/s Run time/s |
|
| Simple model | CNN | 84.33 | 3.25 |
| Attention | 79.67 | 6.06 | |
| GRU | 83.00 | 47.45 | |
| BiGRU | 85.33 | 70.15 | |
| RNN | 80.67 | 20.80 | |
| LSTM | 84.33 | 41.45 | |
| BiLSTM | 85.67 | 54.19 | |
| Complex model | CNN+LSTM | 85.33 | 14.17 |
| BiGRU+Attention | 86.00 | 30.90 | |
| BiLSTM-Attention | 89.00 | 32.22 | |
当原始特征数据未通过RF对音频特征进行筛选,由表 2可以看出:
① 简单模型的平均分类准确率高于复杂模型,且平均运行时间低于复杂模型。说明当数据信息量较大时,相比于复杂模型,简单模型不容易产生过拟合现象,对新数据的泛化能力较好,同时,其更不容易受到数据噪声和不确定性的影响而导致预测错误,更具有鲁棒性。
② 在简单模型中,BiLSTM模型的分类准确率最高,为86.33%,说明BiLSTM模型相较于其他模型具有较好的时间信息学习能力,更适合于音频分类任务。
③ 在复杂模型中,BiLSTM-Attention模型分类准确率最高,为82.67%,说明将BiLSTM模型与注意力机制相融合确实能在一定程度上提高音频分类的准确率。
当原始特征数据通过RF对音频特征进行筛选后,由表 3可以看出:
① BiLSTM-Attention模型的准确率是所有模型中最高的。LSTM网络改进了RNN隐藏层结构,缓解了梯度问题,因此对比RNN其分类准确率有明显提升;BiLSTM模型通过一个前向和一个后向的LSTM网络加强了同时学习时间序列前后信息的能力,因此强于LSTM模型;而BiLSTM-Attention模型在BiLSTM模型的基础上引入注意力机制,加强了模型对于时间序列全局信息同时学习的能力,进一步提高了分类准确率。
② BiLSTM-Attention模型在保证分类准确的同时,运行时间相对较短。由于该模型在BiLSTM模型的基础上加入注意力机制,减缓了BiLSTM网络对序列前后关系的依赖,因此运行时间相对较短;而BiLSTM模型是两个LSTM模型的结合,运算复杂,因此运行时间比LSTM更长;RNN由于内部运算简单,运行时间更短,但准确率较低。
③ 对比所有模型发现,BiLSTM是所有简单模型中对京剧二分类准确率最高的模型,证明BiLSTM模型对音频局部时间信息学习能力较强。单独利用Attention模型进行分类训练,准确率较低,但将注意力机制与其他网络模型结合后,均能提高原始模型分类准确率且缩短运行时间,证明注意力机制能学习音频的全局时间联系,加强模型的学习能力并降低计算难度。因此,结合BiLSTM与注意力机制后的BiLSTM-Attention模型涵盖两个基础模型各自的优势,使得分类准确率达到最优。
根据上述分析可知,本研究提出的RF-BiLSTM-Attention模型对于京剧与其他类型音乐的分类准确率最高,运行时间居中。相较于简单模型中分类准确率最好的RF-BiLSTM模型,RF-BiLSTM-Attention模型的分类准确率提高3.33%,运行时间缩短21.97 s。
从图 11可以看出70%的模型在经过RF预处理后再进行训练得到的准确率更高,说明使用RF对特征进行筛选,能够有效地保留音频本质信息,并减少由于特征过多带来的信息重复所造成的特征冗余,使得模型的分类准确率增加。从图 12可以看出所有模型经过RF预处理后运行时间都比未预处理的运行时间缩短90%以上,说明RF能够有效筛选出重要特征,实现有效降维,使得原始数据复杂度降低,从而减少运行时间。由上述分析可以看出,将RF加入BiLSTM-Attention模型中,能够有效地提高模型的运行速度并提高模型分类准确率。
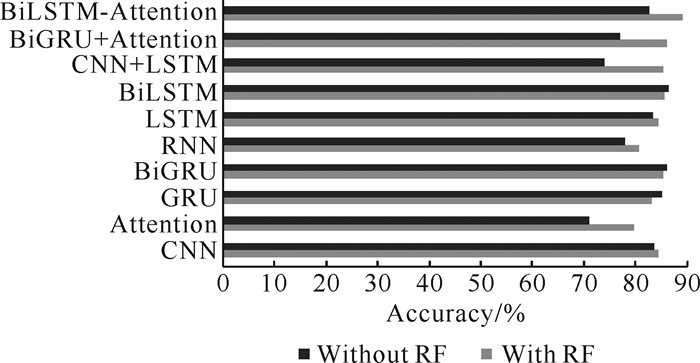
|
| 图 11 有无RF条件下的准确率对比 Fig.11 Comparison of RF accuracy with and without RF |

|
| 图 12 有无RF条件下的运行时间对比 Fig.12 Comparison of RF operating time with and without RF |
将RF-BiLSTM-Attention模型与其部分组件进行比较,可由表 4得出以下结论:
| 神经网络模型 Neural network model |
准确率/% Accuracy/% |
运行时间/s Run time/s |
| BiLSTM | 86.33 | 807.13 |
| RF-BiLSTM | 85.67 | 54.19 |
| Attention | 71.00 | 170.00 |
| RF-Attention | 79.67 | 6.06 |
| BiLSTM-Attention | 82.67 | 1 035.88 |
| RF-BiLSTM-Attention | 89.00 | 32.22 |
① 加入RF对音频特征进行筛选后,能有效降低数据的冗余,减少噪声数据对后续分类准确率造成的影响,以此提高模型分类准确率。同时,筛选特征后,数据维度降低,能使模型训练时间缩短。加入RF的模型的分类准确率最高提高8.67%,运行时间最高减少96.89%。
② 仅在BiLSTM模型的基础上融合Attention时,BiLSTM-Attention模型比BiLSTM模型的分类准确率降低3.66%,说明在数据较为复杂时,由于BiLSTM-Attention模型对数据有更好的学习能力,因此更易产生过拟合现象,导致模型的分类准确率下降。相比于RF-BiLSTM模型,RF-BiLSTM-Attention模型的分类准确率提高3.33%,运行时间缩短40.54%。这是由于注意力机制能够学习音频的局部信息并且不依赖时间帧之间的关系,因此能够提高模型分类准确率并缩短运行时间。
经过模型的各个组件的对比,表明经过RF预处理后的数据再利用耦合了注意力机制的BiLSTM网络,即本研究所提出的RF-BiLSTM-Attention模型,在本研究的分类任务中表现出最佳性能,证实了3个组件的协同效应。
4 结论本研究提出一种RF-BiLSTM-Attention模型用于京剧与其他类型音乐的二分类研究。该模型通过随机森林选择特征变量得分较高的有效特征,然后利用BiLSTM-Attention同时学习音频局部时间信息与全局时间信息。以京剧与其他类型音乐为算例,将RF-BiLSTM-Attention模型与RNN、LSTM、BiLSTM等9种模型进行对比实验,证实RF-BiLSTM-Attention模型可以通过随机森林在不影响时序全局建模的前提下,使用袋外误差衡量初始特征重要性,刻画同序列下的特征重要程度,实现特征维度的降低,减少运行时间;并可利用BiLSTM-Attention学习音频的时间信息,减少因为位置差异而产生的信息损失,增加特征拟合能力,提高模型分类准确率。但该模型在京剧分类时仅根据音频提取出的特征进行分类训练,京剧统计特点及特定特征对于京剧分类效果的影响还有待进一步研究。
| [1] |
王文照. 北京京剧票房运营调研报告: 以"北京新荣春青年京剧社"为例[D]. 北京: 中国艺术研究院, 2021.
|
| [2] |
袁思源. X大学附中"京剧社"发展现状研讨[D]. 重庆: 西南大学, 2018.
|
| [3] |
SAUNDERS J. Real-time discrimination of broadcast speech/music[C]//1996 IEEE International Conference on Acoustics, Speech, and Signal Processing Conference Proceedings. Atlanta, GA, USA: IEEE, 1996, 2: 993-996.
|
| [4] |
SCHEIRER E, SLANEY M. Construction and evalua- tion of a robust multifeature speech/music discriminator[C]//1997 IEEE International Conference on Acoustics, Speech, and Signal Processing. Munich, Germany: IEEE, 1997, 2: 1331-1334.
|
| [5] |
LIM C, CHANG J H. Efficient implementation techni- ques of an SVM-based speech/music classifier in SMV[J]. Multimedia Tools and Applications, 2015, 74(15): 5375-5400. DOI:10.1007/s11042-014-1859-8 |
| [6] |
BIRAJDAR G K, PATIL M D. Speech and music classification using spectrogram based statistical descriptors and extreme learning machine[J]. Multimedia Tools and Applications, 2019, 78: 15141-15168. DOI:10.1007/s11042-018-6899-z |
| [7] |
BIRAJDAR G K, PATIL M D. Speech/music classification using visual and spectral chromagram features[J]. Journal of Ambient Intelligence and Humanized Computing, 2020, 11: 329-347. DOI:10.1007/s12652-019-01303-4 |
| [8] |
姚斯强, 胡剑凌. 线性判别分析和支持向量机的音乐分类方法[J]. 电声技术, 2006, 12: 6-10. DOI:10.16311/j.audioe.2006.12.002 |
| [9] |
万凌艳. 基于特征提取与SVM的多乐器信号快速识别[J]. 自动化与仪器仪表, 2022, 26: 17-21, 26. |
| [10] |
TU W P, YANG Y H, DU B, et al. RNN-based signal classification for hybrid audio data compression[J]. Computing, 2020, 102: 813-827. DOI:10.1007/s00607-019-00713-8 |
| [11] |
ZHANG Z X, LIU D, HAN J, et al. Learning audio sequence representations for acoustic event classification[J]. Expert Systems with Applications, 2021, 178: 115007. DOI:10.1016/j.eswa.2021.115007 |
| [12] |
郭毓博, 陆军, 段鹏启. 基于深度学习的竹笛吹奏技巧自动分类[J]. 应用科学学报, 2021, 39(4): 685-694. |
| [13] |
YU W, HUA M, ZHANG Y. Audio classification using attention-augmented convolutional neural network[J]. Knowledge-Based Systems, 2018, 161: 90-100. DOI:10.1016/j.knosys.2018.07.033 |
| [14] |
NOUMIDA A, RAJEEV R. Multilabel bird species classification from audio recordings using attention framework[J]. Applied Acoustics, 2022, 197: 108901. DOI:10.1016/j.apacoust.2022.108901 |
| [15] |
SCHUSTER M, PALIWAL K K. Bidirectional recur- rent neural networks[J]. IEEE Transactions on Signal Processing, 1997, 45(11): 2673-2618. DOI:10.1109/78.650093 |
| [16] |
HOCHREITER S, SCHMIDHUBER J. Long short- term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [17] |
BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
| [18] |
GENUER R, POGGI J M, TULEAU-MALOT C. Variable selection using random forests[J]. Pattern Recognition Letters, 2010, 31(14): 2225-2236. DOI:10.1016/j.patrec.2010.03.014 |
| [19] |
NIU Z Y, ZHONG G Q, YU H. A review on the attention mechanism of deep learning[J]. Neurocomputing, 2021, 452: 48-62. |



