窃电技术的智能化、多样化和专业化给国家电网及供电公司造成了重大经济损失,对反窃电技术的研究有望为国家电网追回经济损失。然而传统窃电高风险客户定位的研究存在定位不精确、查处耗时的问题,因此需要加强窃电高风险客户精准定位的研究,以提高定位的精准度及高效实时性,保证国家的利益及电网的平稳安全运行,这对电力行业的发展具有重要意义[1, 2]。覃华勤等[3]首先通过动态时间弯曲度量窃电用户的相似性特征,构建相似度矩阵,然后聚类划分窃电高风险客户,并通过簇中心表达,最后在电力系统内通过相似度度量定位出窃电高风险客户。但该方法存在误判率大、定位不精准的问题。蔡嘉辉等[4]首先构建神经网络结构,其次通过神经网络结构完成用电用户的数据特征提取,最后输入特征至随机森林训练分类器来完成窃电用户的检测。但该方法检测时间长、效率低,实际应用效果不佳。马晓琴等[5]获取用电用户数据并对其实行降维处理,通过t-LeNet神经网络完成窃电用户的检测。但该方法的窃电用户检测误判率大,检测效果不佳。为了解决上述方法中存在的问题,本文提出基于多维行为分析的窃电高风险客户精准定位方法,通过对用电用户数据去噪处理,提取用户特征,分析窃电用户特征,根据逻辑回归算法实现窃电用户的精准定位。
1 用户数据去噪处理首先用相关矩阵对用电用户数据信息初步去噪,再利用基于特征值谱熵正则化完成最终的去噪处理[6-8]。
对用电用户数据完成归一化处理。对因电功率序列中的测量误差及用户随机行为引起的噪声干扰,通过相关矩阵R去噪,以提高其准确性。
比较随机矩阵中预测与时间序列的不同,可获得实际数据的偏离值,可表达其行为特征。依照分布概率为1,将随机矩阵收放到极限谱中,密度函数如公式(1)所示:
| $ \begin{gathered} J(\mu)= \\ \left\{\begin{array}{c} \frac{E}{2 {\rm{ \mathsf{ π} }} \sigma^2} \frac{\sqrt{\left(\mu_{\max }-\mu\right)\left(\mu-\mu_{\min }\right)}}{\mu}, \mu_{\min } \leqslant \mu \leqslant \mu_{\max } \\ 0, \text { else } \end{array}, \right. \end{gathered} $ | (1) |
式(1)中,μ表示特征值,μmin和μmax分别为特征值的最小值和最大值,E为极限谱分布函数,σ2为标准方差。
因相关矩阵R的半正定实特性,谱分解公式如公式(2)所示:
| $ A=I \varLambda I^{\mathrm{T}}, $ | (2) |
式(2)中,IIT=O,表示单位矩阵,Λ=diag μ1, μ2, μ3, …, μn,用来表达测量误差与用户随机用电的噪声。
用0表达相关矩阵特征值,以保留真实信息差异,如公式(3)所示:
| $ \varLambda_{\mathrm{NEW}}=\left(\varLambda^{\mathrm{T}}-\varLambda_t^{\mathrm{T}}\right)+\varLambda_0^{\mathrm{T}}, $ | (3) |
式(3)中,Λt表示噪声特征值矩阵,Λ0表示由0组成的矩阵。
去噪后相关矩阵如公式(4)所示:
| $ A_{\mathrm{NEW}}=I \varLambda_{\mathrm{NEW}} I^{\mathrm{T}}, $ | (4) |
设置ANEW的对角元素为1,完成相关矩阵的去噪处理。
因上述去噪并不是实际噪声的准确估计值,为减小滤波误差,进一步基于特征值谱熵正则化去噪。
用谱熵ζDR度量特征值信息,如公式(5)所示:
| $ \left\{\begin{array}{c} \zeta_{\mathrm{DR}}=-\frac{1}{\lg M} \sum\limits_{o=1}^M \Omega(o) \lg \Omega(o) \\ \Omega(o)=\frac{\xi^2(o)}{\sum\limits_{o=1}^M \xi^2(o)} \end{array}, \right. $ | (5) |
式(5)中,ξ(o)表示相关矩阵特征值,M表示特征值参数,Ω(o)表示噪声变量。
当其他特征值为0且只有一个最大特征值时,谱熵大于0;所有特征值距离相等时,特征值谱熵为最大值。
构建正则化特征值f(μ),如公式(6)所示:
| $ \begin{gathered} f(\mu)=\mu-\mu_{\max }+ \\ \mu_{\min }\left(1+\frac{1}{\zeta_{\mathrm{DR}} \lg M} \sum\limits_{l=1}^{o=1} \sum\limits_{o=1}^M \Omega(o) \lg \Omega(o)\right) 。\end{gathered} $ | (6) |
当f(μ)≤0时,用0表示其特征值。依此通过正则化公式完成进一步去噪处理。
2 用户数据特征提取因去噪后的用户数据在维度等方面存在一定的差异,为此利用UFS-MI模型提取用户行为特征向量[9, 10]。UFS-MI是一种基于互信息的无监督特征选择模型,属于过滤型特征排序方法。UFS-MI模型在多维用户数据特征提取时,首先计算出每个特征的相关度,再使用前向顺序搜索,对特征进行重要性评价,最后输出一个有序特征序列。该模型在应用过程中,分析了用户数据相关度、冗余度和条件熵度量等方面多维特征,因此具有较好的多维用户数据特征提取效果。
用条件熵度量特征f的取值[11],如公式(7)所示:
| $ \begin{gathered} J^{\prime}\left(f_y \mid f_{y^{\prime}}\right)= \\ -\sum\limits_{f_{y^{\prime}}} P\left(f_{y^{\prime}}\right) \sum\limits_{f_y} P\left(f_y \mid f_{y^{\prime}}\right) \lg P\left(f_y \mid f_{y^{\prime}}\right), \end{gathered} $ | (7) |
式(7)中,fy、fy′均为随机特征,P(fy|fy′)表示fy条件概率分布对fy′的数学期望。
条件熵的两个特征互信息关系如公式(8)所示:
| $ \begin{array}{l} \ \ \ \ \ \ O\left(f_y ; f_{y^{\prime}}\right)=J\left(f_y\right)-J^{\prime}\left(f_y \mid f_{y^{\prime}}\right)=O\left(f_{y^{\prime}}\right. \text {; } \\ \left.f_y\right), \end{array} $ | (8) |
式(8)中,J(fy)表示fy的不确定性,O(fy′; fy)表示fy′对fy的不确定性减少的程度。通过步进的方式从特征空集D中选择特征,如公式(9)所示:
| $ \left\{\begin{array}{c} \operatorname{score}(f)=\frac{1}{M} \sum\nolimits_{y=1}^M O\left(f_o ; f_y\right) \\ z_1=\underset{1 \leqslant o \leqslant m}{\operatorname{argmax}}\{\operatorname{score}(f)\} \end{array}, \right. $ | (9) |
式(9)中,score(f)为选择特征,fo为最大相关度特征,O(fo;fy)为fo对fy的不确定性减少的程度,z1为选择特征的集合,m表示第m个用户数据。
用整个特征集合的平均互信息表达一个特征的相关度,如公式(10)所示:
| $ \begin{array}{l} \ \ \ \ \ \ \operatorname{Rel}\left(f_o\right)=\frac{1}{M}\left(J\left(f_o\right)\right)+\sum\nolimits_{1 \leqslant y \leqslant m, y \neq o} R\left(f_o ;\right. \\ \left.f_y\right), \end{array} $ | (10) |
式(10)中,R(fo;fy)表示已知特征信息,其值随其他特征信息量的递减而递增。J(fo)为最大相关度特征的不确定性。
特征fo对特征hy的相关度如公式(11)所示:
| $ \operatorname{Rel}\left(h_y \mid f_o\right)=\frac{J^{\prime}\left(h_y \mid f_o\right)}{J\left(f_o\right)} \operatorname{Rel}\left(h_y\right), $ | (11) |
式(11)中,J′(hy|fo)表示特征hy对特征fo度量的取值,Rel(hy)表示特征hy的相关度,将两个特征之间的差异用冗余度表示,如公式(12)所示:
| $ \operatorname{Red}\left(f_o ; h_y\right)=\operatorname{Rel}\left(h_y\right)-\operatorname{Rel}\left(h_y \mid f_o\right) 。$ | (12) |
在选择特征时,全面考虑特征的冗余度及相关度,其重要评价标准(UmRMR)如公式(13)所示:
| $ \begin{aligned} & \operatorname{UmRMR}\left(f_o\right)=\operatorname{Rel}\left(f_o\right)- \\ \max _{h_y \in D}&\left\{\operatorname{Red}\left(f_o ; h_y\right)\right\} 。\end{aligned} $ | (13) |
通过公式(7)-(13)获取最终的用户特征。
3 窃电高风险用户定位结合引言可知,在窃电高风险用户定位过程中,现有研究主要使用的神经网络方法未考虑到用户的冗余度及相关度特征,造成定位效果较差。为此,本研究在利用UFS-MI模型完成用电用户数据特征提取后,依据逻辑回归算法完成窃电用户的定位[12, 13],其步骤如下所示。
① 等比例选取用电数据系统中的正常用电用户及窃电用户的数据作为初始数据,将其分为样本集和测试集两部分。
② 定义训练用户数据样本集为C={c1, c2, …},特征权重向量用ρ表示,其中ρ∈{ρ1, ρ2},数据特征目标函数表示为f(ρ)=ρT×C,类别集合用V∈{V1, V2}表示,允许误差大于0,初始化迭代次数为0。
③ 迭代求解。迭代求解过程如公式(14)所示:
| $ l=l+1, $ | (14) |
式(14)中,l为迭代次数。
④ 用户定位目标函数▽g如公式(15)所示:
| $ \begin{aligned} &\ \ \ \ \ \ \nabla g=\frac{\sum\limits_{c_z \in C, V=V_1} P_{z 1} P_{z 2} c_z}{P_{z 1}+M}- \\ & \frac{\sum\limits_{c_z \in C, V=V_1} P_{z 1} \sum\limits_{c_z \in C, V=V_1} P_{z 1} P_{z 2} c_z}{\left(\sum\limits_{c_z \in C, V=V_1} P_{z 1}+M\right)^2}, \end{aligned} $ | (15) |
式(15)中,V表示类别,cz表示z个数据样本,Pz1、Pz2表示实例个数,M表示特征值参数。
⑤ 判断目标函数是否成立,如公式(16)所示:
| $ \left\|\nabla g\left(\rho^{(l+1)}\right)\right\|>\varphi 。$ | (16) |
若结果成立,即为最优目标函数,继续执行下一步骤;若不成立,则更新特征权重向量,如公式(17)所示:
| $ \rho^{(l+1)}=\rho^{(l)}+\mu f^{(l)}, $ | (17) |
式(17)中,f为特征值。公式(17)的特征权重向量更新过程中主要使用粒子群方法。通过粒子在搜索空间的初始化更新结果,找出最佳粒子位置,实现粒子寻优以及特征权重向量更新。
根据公式(17)的计算结果更新后返回步骤③。
⑥ 构建最优化目标函数的窃电用户诊断模型,如公式(18)所示:
| $ P\left(V=V_1 \mid c_k\right)=\frac{1}{1+r^{-r^{\rm T}} c_k}, $ | (18) |
式(18)中,ck表示测试样本数据,r表示样本矩阵。求解窃电用户诊断模型,并将求解结果与类别比例概率进行对比,分类最终的用户用电数据样本。
⑦ 测试数据集参数,看其是否为窃电用户[14, 15];当不满足窃电用户要求时,返回步骤②,重新为ρ赋值;满足窃电用户要求时,则进入步骤⑧。
⑧ 完成窃电用户诊断模型构建,输出检测结果。
通过上述步骤,完成最终的窃电高风险用户定位检测。
4 实验与结果分析为验证基于多维行为分析的窃电高风险客户精准定位方法的整体有效性,设计以下测试。
选用某个省份的真实居民用电用户数据信息及大型企业用电用户数据信息作为实验对象。其中,真实居民正常的用电用户数量为600户,其中窃电用户数量为98户;大型企业正常的用电用户数量为240户,其中窃电用户数量为54户。采用实验环境为Windows 10系统下的SPSS数据分析软件,根据窃电用户诊断模型分析用户数据特征,利用MATLAB软件模拟居民用户并输出仿真测试结果。根据上文的窃电高风险客户定位过程进行测试,可将测试过程分为模型训练和模型测试两部分,如图 1所示。
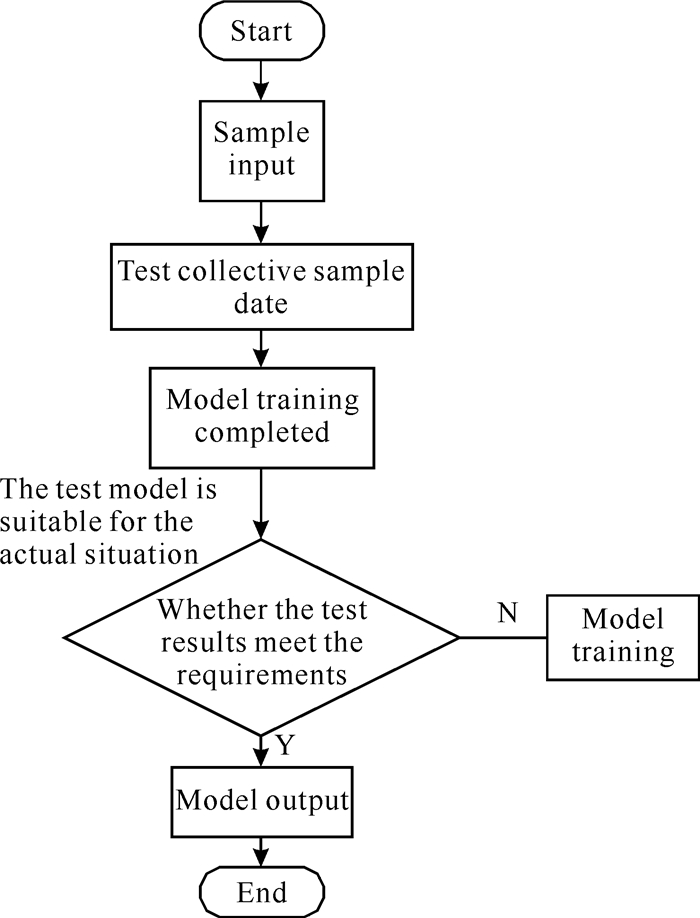
|
| 图 1 窃电高风险客户定位测试流程 Fig.1 Positioning test process for high-risk customers of power theft |
根据上述流程,得到6类居民窃电用户及4类大型企业窃电用户的用电量图,如图 2、图 3所示。
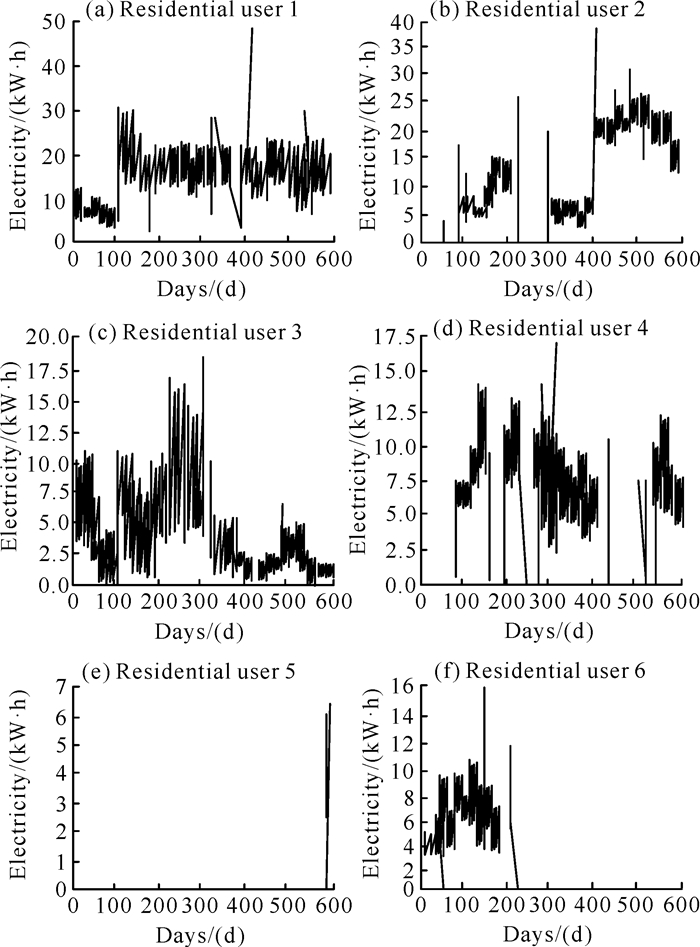
|
| 图 2 居民窃电用户用电量 Fig.2 Electricity consumption of residential users with electricity theft behavior |
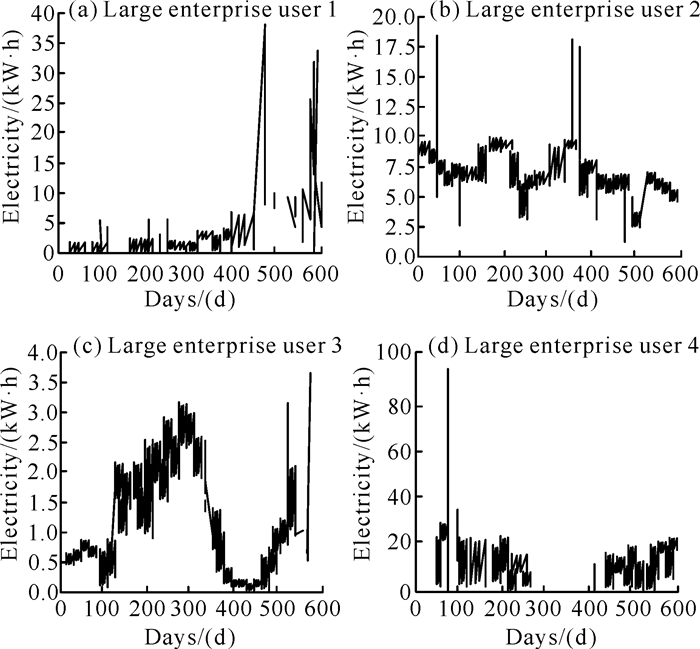
|
| 图 3 大型企业窃电用户用电量 Fig.3 Electricity consumption of large enterprises users with electricity theft behavior |
① 用电量检测。随机选取一段50 h的用电数据,采用本文所提方法、覃华勤等[3]的方法(以下简称方法1)和蔡嘉辉等[4]的方法(以下简称方法2)完成窃电高风险客户的用电量检测,其结果如图 4所示。
由图 4可知,本文所提方法的居民窃电用户用电量检测结果、大型企业窃电用户用电量检测结果与实际电量趋近一致,所提方法可以检测到电量骤降的现象,如居民窃电用户用电量在15、25、40 h发生了电量骤降现象,企业用电用户电量在25 h发生了骤降,之后出现先缓慢下降后上升的趋势。而方法1和方法2的用电量检测存在较大偏差,不能很好地检测出窃电用户用电量,表明本文所提方法对窃电高风险客户的定位检测效果更好。
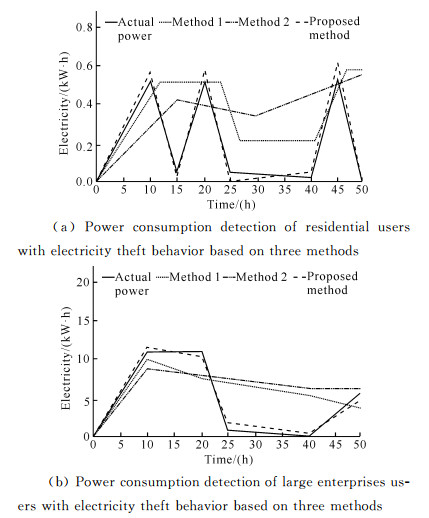
|
| 图 4 基于3种方法的两种类型窃电用户用电量检测 Fig.4 Power consumption detection for two types of users with electricity theft behavior based on three methods |
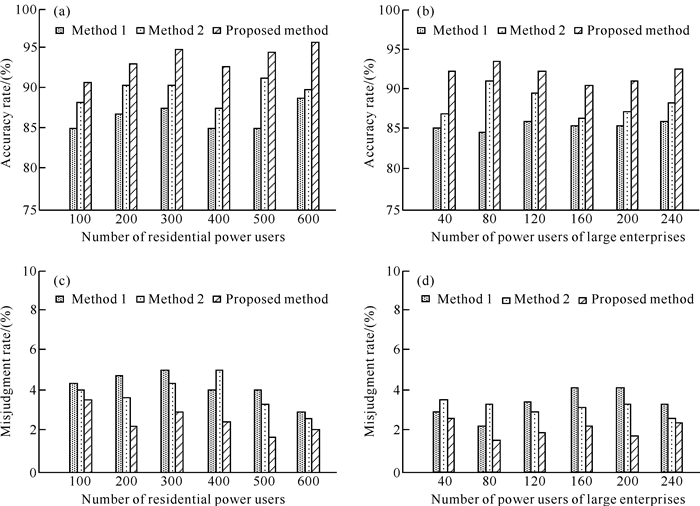
② 准确率及误判率。采用本文所提方法、方法1和方法2分别对600户居民用电用户及240户企业用电用户的窃电行为进行准确率及误判率测试,如图 5所示。由图 5可知,对于600户居民用电用户来说,本文所提方法的准确率高于91%,最大值达到95%,方法1和方法2的准确率最大值分别为90%和87%,且本文所提方法、方法1和方法2的误判率分别低于3.8%、4.7%和4.7%。对于240户企业用电用户来说,本文所提方法的准确率高于90.5%,最大值达到93.7%,方法1和方法2的准确率最大值分别为91%和86.5%,且本文所提方法、方法1和方法2误判率分别低于2.3%、3.4%和4.1%。因此,本文所提方法的居民用电用户及大型企业用电用户的准确率均高于方法1和方法2,本文所提方法的两种类型用电用户的误判率均低于方法1和方法2。综上所述,本文所提方法对窃电高风险客户定位的效果更好。主要原因是本文所提方法在传统窃电高风险用户定位的基础上,增加用户去噪处理,降低检测干扰,并且依据逻辑回归算法提高了窃电用户定位的精确度,使所提方法具有良好的实际应用效果及较高的准确率。
|
| 图 5 3种方法的准确率及误判率 Fig.5 Accuracy rate and misjudgment rate of three methods |
5 结论
对窃电用户的查处可为国家电网及供电公司挽回经济损失,并保证供电设备的正常运行。本文提出基于多维行为分析的窃电高风险客户精准定位方法,首先对用户数据进行去噪处理,其次提取用电用户特征,最后完成窃电高风险客户的定位检测。实验结果表明,本文所提方法检测的用电量与实际用电量较为接近,且对用电用户判断的准确率高于两种对比方法,误判率低于两种对比方法。本文所提方法为电力系统的可持续发展奠定了基础,但仍有不足之处,如特征值提取过程计算量较大,希望在今后的研究中能进一步简化特征值提取过程。
| [1] |
赵云, 肖勇, 曾勇刚, 等. 一种相关性与聚类自适应融合技术窃电检测方法[J]. 南方电网技术, 2021, 15(9): 69-74. |
| [2] |
耿俊成, 张小斐, 周庆捷, 等. 基于局部离群点检测的低压台区用户窃电识别[J]. 电网与清洁能源, 2019, 35(11): 30-36. |
| [3] |
覃华勤, 梁叶, 钱奇, 等. 基于典型窃电用户相似性检索的窃电行为检测方法[J]. 电力系统自动化, 2022, 46(6): 58-65. |
| [4] |
蔡嘉辉, 王琨, 董康, 等. 基于DenseNet和随机森林的电力用户窃电检测[J]. 计算机应用, 2021, 41(S1): 75-80. |
| [5] |
马晓琴, 薛晓慧, 罗红郊, 等. 基于t-LeNet与时间序列分类的窃电行为检测[J]. 华东师范大学学报(自然科学版), 2021(5): 104-114. |
| [6] |
桂团福, 邓居智, 李广, 等. 数学形态学和K-SVD字典学习在大地电磁数据去噪中的应用[J]. 中国有色金属学报, 2021, 31(12): 3713-3729. |
| [7] |
甘若, 陈天伟, 郑旭东, 等. 改进小波阈值函数在变形监测数据去噪中的应用[J]. 桂林理工大学学报, 2020, 40(1): 150-155. |
| [8] |
戚连刚, 申振恒, 王亚妮, 等. 基于周期截断数据矩阵奇异值分解的干扰抑制技术[J]. 电子与信息学报, 2022, 44(6): 2143-2150. |
| [9] |
张林兵, 郭强, 吴行斌, 等. 基于多维行为分析的用户聚类方法研究[J]. 电子科技大学学报, 2020, 49(2): 315-320. |
| [10] |
肖丽莎, 王红军, 杨燕. 基于属性依赖的混合约束半监督特征选择[J]. 计算机应用, 2015, 35(S2): 80-84. |
| [11] |
林克正, 张元铭, 李昊天. 信息熵加权的HOG特征提取算法研究[J]. 计算机工程与应用, 2020, 56(6): 147-152. |
| [12] |
肖弋. 一种新的特征变换算法在网络数据安全检查中应用研究[J]. 科技通报, 2019, 35(5): 127-131. |
| [13] |
熊熙, 乔少杰, 韩楠, 等. 一种基于模糊选项关系的关键属性提取方法[J]. 计算机学报, 2019, 42(1): 190-202. |
| [14] |
陈钢, 李德英, 陈希祥. 基于改进XGBoost模型的低误报率窃电检测方法[J]. 电力系统保护与控制, 2021, 49(23): 178-186. |
| [15] |
殷涛, 薛阳, 杨艺宁, 等. 基于向量自回归模型的高损线路窃电检测[J]. 中国电机工程学报, 2022, 42(3): 1015-1024. |


