2. 北京理工大学机电学院, 北京 100081;
3. 广西科技大学机械与汽车工程学院, 广西柳州 545616
2. School of Mechatronical Engineering, Beijing Institute of Technology, Beijing, 100081, China;
3. School of Mechanical and Automotive Engineering, Guangxi University of Science and Technology, Liuzhou, Guangxi, 545616, China
随着生活水平的提高以及社会的快速发展,我国已经进入老龄化社会,脑卒中和意外事故等造成的运动障碍患者数量呈现增长趋势。目前,针对这类患者的康复治疗方案主要依靠传统的治疗模式和治疗师的经验,难以满足高强度重复训练的要求,而且还缺少经验丰富的康复医师、专业护士以及高端的康复设备。因此,针对下肢运动功能障碍人员进行康复训练已成为亟待解决的重大社会问题[1-4]。近年来,伴随着机器人技术在康复医学中的逐步应用,医工结合得以发展,人们对智能康复器械的需求大幅度增加,结合人体姿态行为识别与机器人的运动控制技术成为研究的热点。
人体姿态实时识别技术基于多传感数据来检测人体行为,可实现对人体姿态变化的有效判别[5]。陈盛等[6]针对肩关节康复患者开发一种镜像康复训练系统,用sEMG装置感知患者上肢肌电信息从而解析实时姿态,控制机器人跟随患者做镜像同步运动,取得了较好的康复训练效果。蒋亚杰[7]引入可以获取人体骨骼图像的Kinect体感设备,获取人体关节点等深度数据,进而提取人体骨骼相关数据流信息,并通过建立运动学方程,把操作者手指姿态转化为机器人关节运动数据信息,完成对机器人的运动控制。为降低机器人与患者运动意图之间的误差,许多学者通过传感器数据对机器人实现运动控制。唐彪等[8]通过视觉感知机器人控制系统对视觉图像进行处理并得到人体关节数据等信息,实现控制远端机器人实时跟随人体运动。Bošnak和Škrjanc[9]使用多个倾角传感器对患者的运动意图进行判断,最后通过PID算法控制机器人。Homich等[10]利用磁力计和陀螺仪计算人体与机器人之间的位姿偏差,通过补偿位姿偏差,使机器人与人体运动姿态趋于一致。伊蕾等[11]设计一种模糊控制器,该控制器可降低移动单元转弯及推力突变对使用者造成的伤害,并实现人机协调运动。上述人体姿态识别方法通过人体肌电信号或机器视觉来提取人体的运动状态,这些方法虽然识别率较高,但是都要求使用者在身体的不同部位固定一定数量的传感器或设置机器人系统可识别的颜色标记。由于使用者的身体状况和环境等因素会干扰系统正常运行,系统有可能做出错误判断,导致机器人的控制误差较大。
针对上述问题和所研制机器人的特点,本研究提出一种在主动跟随模式下基于人体行走姿态来控制机器人运动的控制技术。在控制系统的构建中,数据采集系统将人体的运动速度数据作为机器人跟随运动速度的控制输入,并采用基于模糊PID算法的控制器补偿跟随运动中的误差,使得下肢康复机器人能够较好地按照人体的姿态变化有效跟随人体运动,且在辅助人体运动的同时对其进行实时保护。
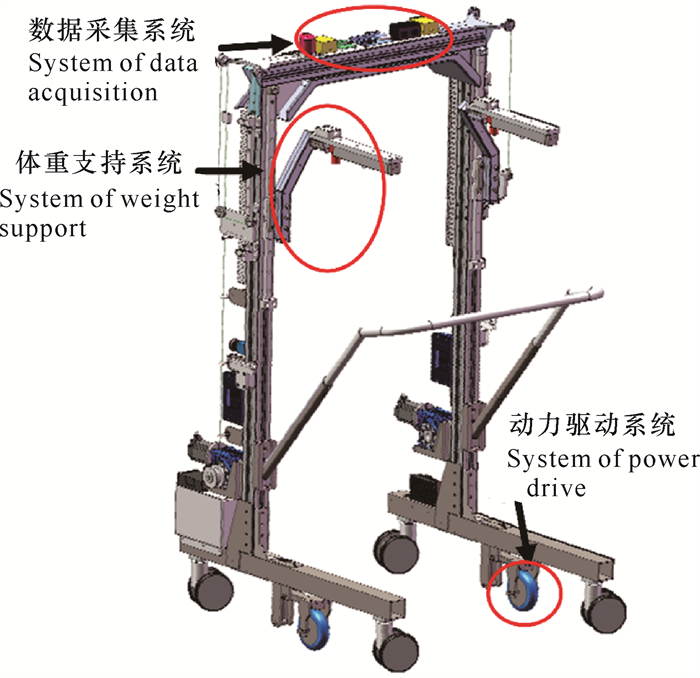
1 康复机器人系统介绍如图 1所示,下肢康复机器人主要由人体运动数据采集系统、为患者提供辅助力的体重支持系统和驱动机器人运动的驱动系统3个部分构成。患者在使用康复机器人进行下肢康复训练时需要身穿减重服,依靠体重支持系统为其提供的辅助力实现下肢站立,另外,体重支持系统还能对个体特征和病患程度不同的患者提供全方位的行走保护。在康复过程中,数据采集系统和动力驱动系统是实时伺服工作的,可共同帮助患者进行行走训练。此外,体重支持系统通过给下肢力量不足的患者施加辅助的外力支持,减轻患者下肢负担。体重支持系统装置上安装有传感器,能够实时检测人体姿态行为的变化,人体运动带动体重支持系统上面的位移传感器,使得位移数值发生变化。数据采集系统根据实时检测的位移变化量,对这些数据进行信息分析,得到下肢康复机器人的控制指令,从而达到实时跟随使用者运动的目的。
|
| 图 1 下肢康复机器人结构图 Fig.1 Structure diagram of lower limb rehabilitation robot |
1.1 数据采集系统传感器的结构布置
人体姿态行为识别主要通过布置在数据采集系统上的传感器采集人体的行为信息,然后通过行为识别算法来实现。为实时获取人体行为的变化数据,并准确获取肢体的运动信息,需要对现实状况下感知人体行为的传感器进行配置。正常人在行走过程中,为了维持平衡和移动重心,上部肢体会自然产生左右摆动的运动特征,而在转身过程中身体会有较明显的转向特点。通过对正常人行走姿态的研究分析,对使用者行走、转弯和停止的数据进行总结并归类,结合传感器系统确定所需的感知信息、传感器类型数量以及传感器的位置。在下肢康复机器人系统中,经过对人体行走姿态的运动分析可知,人体肩部摆动距离变化值是主要的感知信息,这一信息在使用者行走过程中起关键的作用,因此位移传感器结构布置如图 2所示。

|
| 图 2 位移传感器结构布置图 Fig.2 Structure layout diagram of displacement sensor |
1.2 数据采集系统硬件
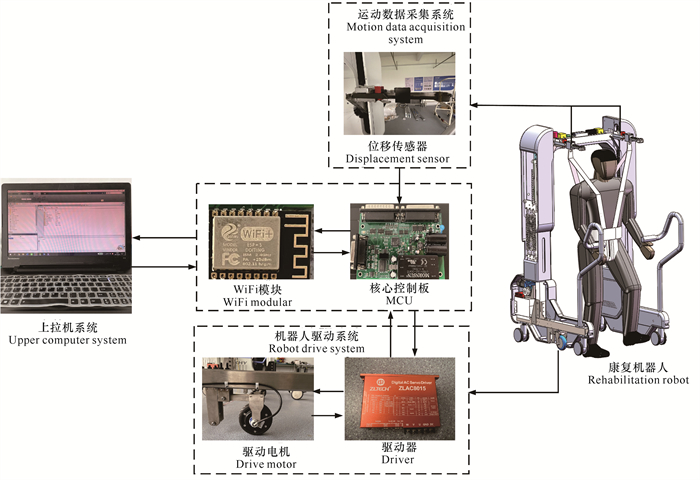
康复机器人的数据采集系统由位移传感器和主控板组成。位移传感器的反馈数据是康复机器人运动控制的基础,通过搭建数据采集电路实现位移数据的实时采集。上位机数据采集处理系统和康复机器人通过WiFi模块完成运动数据的交互,该模块的传输速率为54 Mbps,有效传输距离为100 m,具有传输速率快、距离远、抗干扰能力强和使用简单的优点,数据采集系统的硬件结构如图 3所示。
|
| 图 3 运动数据采集系统的硬件结构 Fig.3 Hardware structure of motion data acquisition system |
首先,体重支持系统两侧的位移传感器实时感知患者肩部的位移信息,并将位移信息反馈至机器人的主控板上。然后主控板的WiFi模块将人体姿态运动数据传输至上位机,上位机对运动数据进行预处理,提取时域特征,并进行分析识别,通过算法计算人体所处状态及运动趋势。最后,上位机得出驱动轮的期望运动速度并发送至主控板,机器人主控系统通过CAN通信向驱动器发送速度控制指令,实现控制机器人跟随运动的目标。
1.3 数据采集系统数据处理为提高姿态行为识别的准确性,需要对采集的数据进行预处理,剔除运动数据中的噪声,使数据更接近真实情况。本研究采用滑动平均滤波方法对运动数据进行预处理,由于机器人主控板控制周期为30 ms,所以将传感器数据采样频率f设置为1 kHz,数据采集长度N设为15,滤波数据处理流程如图 4所示。

|
| 图 4 滑动平均滤波数据处理流程 Fig.4 Data processing flow of moving average filtering |
由图 5可知,滤波前位移值存在较大的抖动现象,滤波后位移值变得平滑,有利于人体姿态变化特征的分析。

|
| 图 5 位移曲线滤波前后对比 Fig.5 Comparison of displacement curve before and after filtering |
数据采集系统采集电机当前速度和编码器数据上传至上位机,上位机结合当前电机电流、电压等信息,借助卡尔曼滤波器,降低速度值噪声,减少观测不准确的情况,综合得出机器人当前真实速度。由图 6可知,在滤波前速度值变化快,匀速运动过程有较大抖动,在经过卡尔曼滤波法处理后,速度曲线更有利于人体运动姿态的识别。

|
| 图 6 转速曲线滤波前后对比 Fig.6 Comparison of speed curve before and after filtering |
2 机器人运动学模型的构建
本文研究的下肢康复机器人主要是为脑卒中中后期患者所设计的。为方便患者能够在原地转弯,底盘采用六轮分布结构,同一轴线上有3个轮,驱动轮中置,两个万向轮前后置,采用差速控制,理论上不考虑机器人侧滑和打滑的现象。下肢康复机器人运动学模型如图 7所示,{O, X, Y}为全局坐标系,{P, Xc, Yc}为局部坐标系,x、y分别表示机器人在全局坐标系中的横、纵坐标,θ为两坐标系的夹角。

|
| 图 7 下肢康复机器人运动学模型 Fig.7 Kinematics model of lower limb rehabilitation robot |
设机器人每个驱动轮直径为2r,两侧驱动轮间距为2b,在局部坐标系下的速度为v。当机器人几何中心与质心重合,机器人运行方向与驱动轮轴方向垂直,那么在车轮不打滑情况下构建非完整约束方程:
| $ \dot x\;{\rm{sin}}\theta - \dot y\;{\rm{cos}}\theta = 0, $ | (1) |
写成矩阵形式为
| $ A\left( q \right)\dot q = 0, $ | (2) |
式中:A(q)=[-sinθ, cosθ, 0];
| $ \dot q = S\left( q \right)V(t), $ | (3) |
式中:S(q)是一个Jacobian矩阵,V(t)=[vp, wp]T,vp为P点线速度,wp为P点角速度,则运动学方程可表示为
| $ \dot q = \left[ {\begin{array}{*{20}{c}} {\dot x}\\ {\dot y}\\ {\dot \theta } \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{\rm{cos}}\theta }&0\\ {{\rm{sin}}\theta }&0\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{v_p}}\\ {{\omega _p}} \end{array}} \right]。$ | (4) |
建立位移传感器位移量与机器人驱动轮转速之间的关系,确定康复机器人期望控制输入为
| $ {v_r} = \frac{{\zeta {\rm{ }}\left( {{x_1} + {x_2}} \right)}}{2}, $ | (5) |
| $ {w_r} = \frac{{\zeta {\rm{ }}\left( {{x_1} - {x_2}} \right)}}{{2b}}, $ | (6) |
式中:vr为机器人运动期望线速度,wr为机器人运动期望角速度,x1和x2为左右两侧位移传感器变化值,ζ为位移与驱动轮转速之间的线性系数。
假如qr=[xr, yr, θr]T表示人体运动的给定参考轨迹位姿,q=[x, y, θ]T表示移动机器人的实际位姿,实际位姿每一时刻的变化值与肩部摆动距离变化值成线性关系,则定义轨迹误差qe为
| $ \begin{array}{l} {q_e} = \left[ {\begin{array}{*{20}{c}} {{e_1}}\\ {{e_2}}\\ {{e_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{x_e}}\\ {{y_e}}\\ {{\theta _e}} \end{array}} \right]{\rm{ }} = \\ \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\theta }&{{\rm{sin}}\theta }&0\\ { - {\rm{sin}}\theta }&{{\rm{cos}}\theta }&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_r} - {x_p}}\\ {{y_r} - {y_p}}\\ {{\theta _r} - {\theta _p}} \end{array}} \right] = {T_e}\left( {{q_r} - q} \right), \end{array} $ | (7) |
式中:{xr, yr, θr}为给定参考轨迹的坐标,{xp, yp, θp}为实际轨迹的坐标;Te为转换矩阵。对式(7)求导得到微分方程为
| $ {\dot q_e} = \left[ {\begin{array}{*{20}{c}} {{{\dot e}_1}}\\ {{{\dot e}_2}}\\ {{{\dot e}_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\dot x}_e}}\\ {{{\dot y}_e}}\\ {{{\dot \theta }_e}} \end{array}} \right]{\rm{ }} = \left[ {\begin{array}{*{20}{c}} {\omega {y_e} - {v_p} + {v_r}{\rm{cos}}{\theta _e}}\\ {{\rm{ - }}\omega {x_e} + {v_r}{\rm{sin}}{\theta _e}}\\ {{\omega _r} - {\omega _p}} \end{array}} \right]。$ | (8) |
设计一个平滑的速度控制Vc=f(Ve, vr, K),其中K=[Kp, Ki, Kd]T。根据误差公式(8)及参考文献[12]的思想,选择适当的Lyapunov函数设计协助速度控制输入Vc,则Vc可表示如下:
| $ {V_c} = \left[ {\begin{array}{*{20}{c}} {{v_c}}\\ {{w_c}} \end{array}} \right]{\rm{ }} = \left[ {\begin{array}{*{20}{c}} {{v_r}{\rm{cos}}{\theta _e} + {k_1}{x_e}}\\ {{w_r} + {k_2}{v_r}{y_e} + {k_3}{v_r}{\rm{sin}}{\theta _e}} \end{array}} \right], $ | (9) |
式中:k1,k2,k3是控制器的设计参数,均大于0。Vc作为协助速度控制量输入,使得康复机器人的位姿误差qe趋于零,即
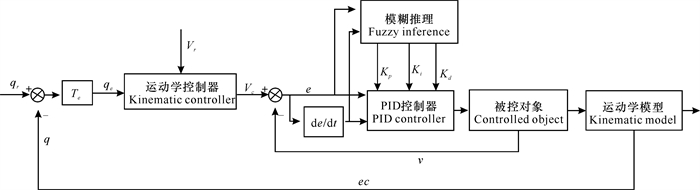
在实际应用中,模糊PID控制器的输入为康复机器人的期望速度,反馈值为驱动轮的实际速度,具体结构如图 8所示。
|
| 图 8 模糊PID控制器的结构 Fig.8 Structure of fuzzy PID controller |
3.1 速度输入输出模糊化和隶属度函数
模糊PID控制器中给定的转速和机器人实际速度之间的偏差值e、偏差变化率ec在模糊集上的论域为[-6, 6],输出量PID参数ΔKp、ΔKi、ΔKd的基本论域分别为[-15, 15]、[-13, 13]、[-2, 2],模糊子集为{NB,NM,NS,ZO,PS,PM,PB},分别对应{负大,负中,负小,零,正小,正中,正大}。
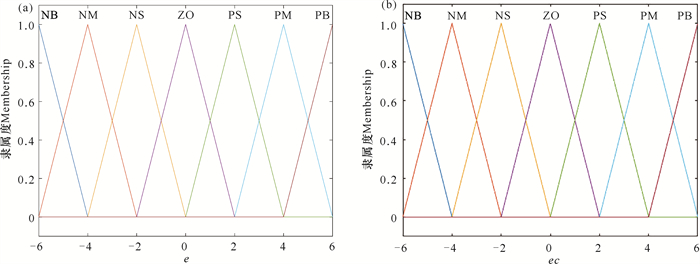
如图 9所示,采用计算量相对较小且易于实现的三角隶属度函数来确定模糊语言变量的隶属度。
|
| 图 9 偏差值e (a)和偏差变化率ec (b)三角隶属度函数 Fig.9 Triangular membership function of deviation value e (a) and deviation rate ec (b) |
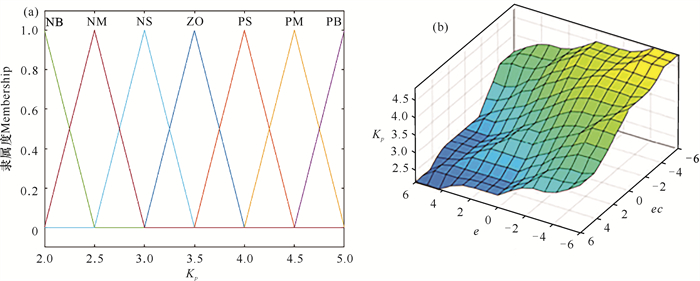
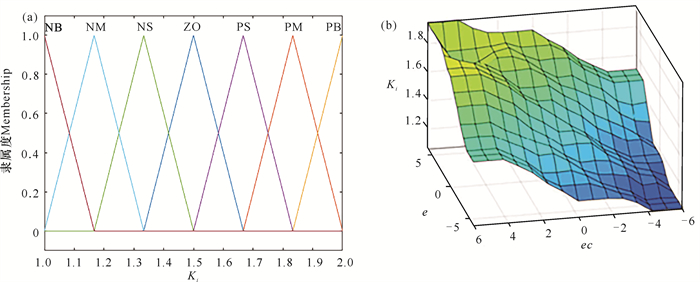
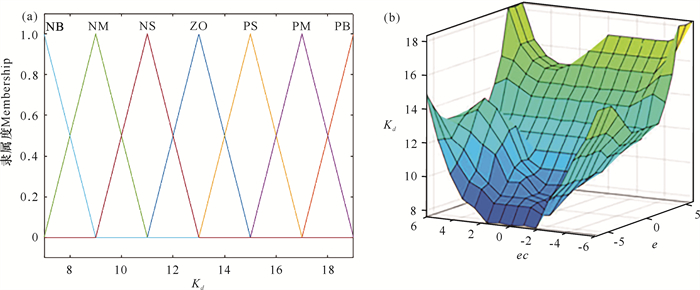
由Matlab模糊控制工具箱得出,输出量PID参数ΔKp、ΔKi、ΔKd的基本论域取值范围与偏差值e、偏差变化率ec的对应图像(图 10-12),则可得出ΔKp、ΔKi、ΔKd在实际计算过程中的取值范围。
|
| 图 10 ΔKp基本论域(a)及其与e、ec的对应关系(b) Fig.10 Basic theoretical domain ΔKp (a) and its corresponding relation with e and ec (b) |
|
| 图 11 ΔKi基本论域(a)及其与e、ec的对应关系(b) Fig.11 Basic theoretical domain ΔKi (a) and its corresponding relation with e and ec (b) |
|
| 图 12 ΔKd基本论域(a)及其与e、ec的对应关系(b) Fig.12 Basic theoretical domainΔKd (a) and its corresponding relation with e and ec (b) |
3.2 模糊规则建立
通过查找相关资料和不断反复调试,确定如下模糊规则:
当误差|e|和误差变化率|ec|较小时,输入误差较小,应优先考虑系统的抗干扰性和稳定性,Kp,Ki和Kd取值应大一些;
当误差|e|和误差变化率|ec|均为中等大小时,优先降低系统的超调量,考虑响应速度和调节时间,Kp取值应小一些;
当误差|e|和误差变化率|ec|较大时,输入误差较大,应优先考虑系统的跟踪准确性,防止因微分饱和引起的超调变大,Kp取值应大一些,此时取Ki=0。
根据以上规则制定模糊规则表,如表 1-3所示。{NB,NM,NS,ZO,PS,PM,PB}分别对应{负大,负中,负小,零,正小,正中,正大},算法在计算时依据|e|和|ec|的输入范围,对应表格对Kp,Ki和Kd取值。
| ec | e | ||||||
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PB | PB | PM | PM | PS | ZO | ZO |
| NM | PB | PB | PM | PS | PS | ZO | NS |
| NS | PM | PM | PM | PS | ZO | NS | NS |
| ZO | PM | PM | PS | ZO | NS | NM | NM |
| PS | PS | PS | ZO | NS | NS | NM | NM |
| PM | PS | ZO | NS | NM | NM | NM | NB |
| PB | ZO | ZO | NM | NM | NM | NB | NB |
| ec | e | ||||||
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | NB | NB | NM | NM | NS | ZO | ZO |
| NM | NB | NB | NM | NS | NS | ZO | ZO |
| NS | NB | NM | NS | NS | ZO | PS | PS |
| ZO | NM | NM | NS | ZO | PS | PM | PM |
| PS | NM | NS | ZO | PS | PS | PM | PB |
| PM | ZO | ZO | PS | PS | PM | PS | PB |
| PB | ZO | ZO | PS | PM | PM | PB | PB |
| ec | e | ||||||
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PS | NS | NB | NB | NB | NM | PS |
| NM | PS | NS | NB | NM | NM | NS | ZO |
| NS | ZO | NS | NM | NM | NS | NS | ZO |
| ZO | ZO | NS | NS | NS | NS | NS | ZO |
| PS | ZO | ZO | ZO | ZO | ZO | ZO | ZO |
| PM | PB | PS | PS | PS | PS | PS | PB |
| PB | PB | PM | PM | PM | PS | PS | PB |
3.3 模糊推理与解模糊化
由于被控对象必须是一个精确的控制量,但依据上述模糊规则输入被控速度值后得到的是一个模糊集合,所以使用计算量小、计算过程相对简单的加权平均法来解模糊,确定最终能够代表模糊集合的单值,计算过程如下:
| $ u = \frac{{\sum \mu \left( {{u_i}} \right){u_i}}}{{\sum u\left( {{u_i}} \right)}}, $ | (10) |
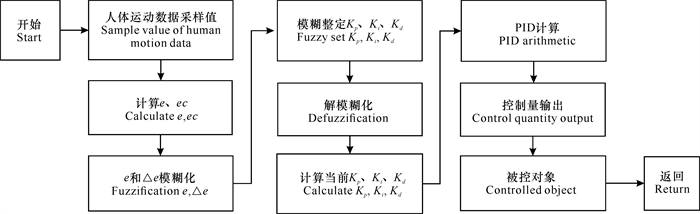
式中:u为解模糊后的精确值,ui为模糊变量的元素,μ(ui)为ui元素相对应的隶属度。控制器根据机器人的速度输入e和ec,依此调节Kp,Ki,Kd并得到最终的整定参数,可用公式表示为kx=△kx+k′x。模糊推理流程如图 13所示。
|
| 图 13 模糊推理流程图 Fig.13 Flow chart of fuzzy reasoning |
4 运动控制系统仿真与实验 4.1 运动控制系统仿真
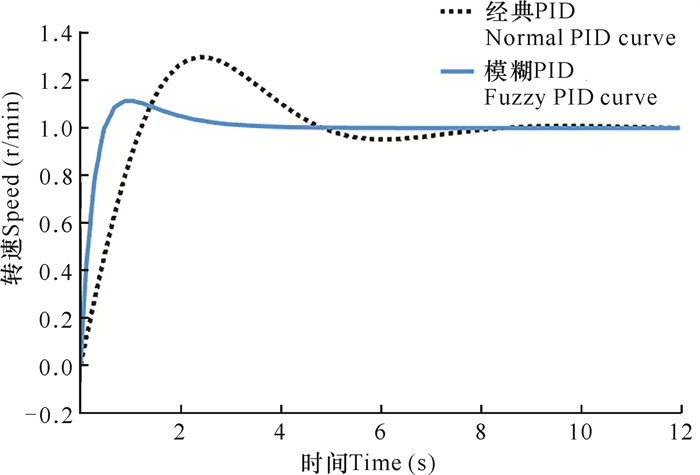
搭建康复机器人的运动控制仿真模型。由于PID的参数在调试过程中是相互影响的,所以在确定PID参数时要先确定PI控制器,经试凑法确定Kp=500,Ki=100,最后在此基础上确定Kd的值。为保证系统稳定性与安全性,Kp的值不宜过大;为减小超调量,Ki的值不宜过小,最终确定Kp=500,Ki=100,Kd=20。由图 14可知,在输入为阶跃响应时,模糊PID控制器响应曲线较为平滑,1 s内达到稳定状态;而经典PID控制响应曲线的超调量达到11%,大约6 s后才趋于平稳。由此可知,模糊PID不论从调节时间、上升时间还是稳定性上来说都具有更大的优势。
|
| 图 14 模糊PID与经典PID对比图 Fig.14 Fuzzy PID vs normal PID |
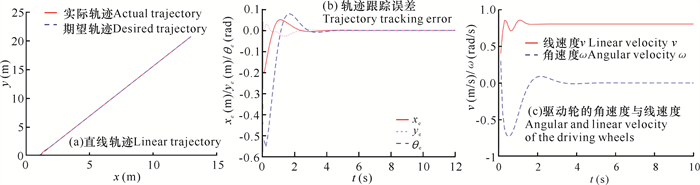
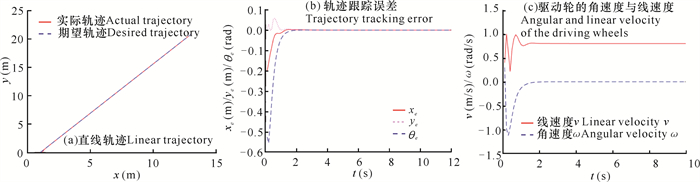
设机器人初始位姿为(0,0,π/4),参考轨迹为y=x,期望速度为0.8 m/s,期望角速度为0 rad/s。从图 15a、b中可以看出在开始一段时间内,经典PID直线轨迹跟踪精度较差,误差较大,在大约5 s后跟踪误差逐渐趋于0;而从图 15c中可以看出,运动过程中线速度与角速度在大约5 s后稳定。模糊PID直线轨迹跟踪和误差曲线如图 16所示,从图 16b中可以看出在给定参考轨迹下,在大约3 s左右跟踪误差趋于0;而从图 16c中也可以看出, 运动过程中线速度与角速度曲线在大约3 s后稳定。对比两种控制算法,模糊PID控制算法跟踪响应速度更高,实时性更好。
|
| 图 15 经典PID直线轨迹跟踪和误差曲线 Fig.15 Normal PID linear trajectory tracking and error curve |
|
| 图 16 模糊PID直线轨迹跟踪和误差曲线 Fig.16 Fuzzy PID linear trajectory tracking and error curve |
4.2 运动控制实验
本研究选取1名身高177 cm、体重70 kg的测试对象参与康复机器人运动控制实验。在实验过程中志愿者需要穿着减重服,志愿者的身体左右两侧的体重支持数值均设定为18 kg,确保志愿者身体处于一种近似平衡的状态。在康复训练过程中不需要人为控制机器人的运动,系统将志愿者的位姿变化信息作为机器人的控制输入。实验主要验证机器人根据传感器数据识别当前使用者身体姿态变化对实现下肢康复机器人运动控制的正确性和可靠性,实验重复3次,最后取3次实验数据的平均值,实验现场如图 17所示。

|
| 图 17 实验测试过程 Fig.17 Experimental test process |
4.3 实验分析
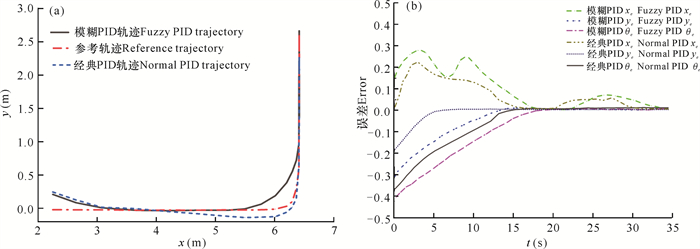
实验过程中,测试者沿着目标轨迹行走,实际轨迹则通过机器人电机编码器反馈的数据计算获得。如图 18a所示,红色虚线为机器人行进的参考轨迹,黑色实线所对应的模糊PID控制方法在起步时与参考轨迹误差更小,转弯时能够提前做出转弯动作,经典PID轨迹在4 m后和参考轨迹误差逐渐加大。由机器人直行-左转-直行过程中的模糊PID与经典PID轨迹误差值(图 18b)可知,在15 s左右时误差逐渐收敛;20 s后机器人左转,角度产生较大的误差;30 s左右机器人误差趋于零并保持稳定,总体上模糊PID控制优于传统PID。
|
| 图 18 机器人行进中轨迹(a)和轨迹误差曲线(b) Fig.18 Trajectory (a) and trajectory error (b) curves in robot moving |
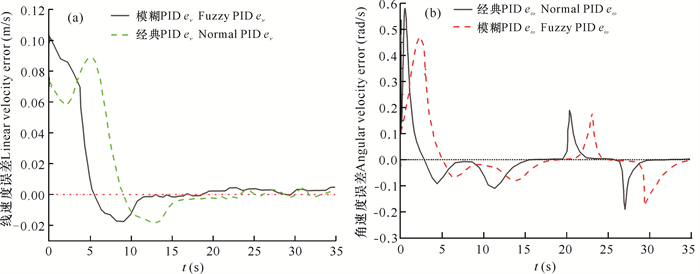
图 19为机器人在直行-左转-直行实验过程中驱动轮线速度和角速度的误差值变化过程。由运动过程中线速度误差ev变化(图 19a)可知,在直行过程中,上位机根据位移信息综合判断识别当前运动姿态,实时调整机器人直行速度。在机器人开始运动后20 s,上位机对人体运动数据综合分析后,判定当前为直行-左转状态,导致角速度发生变化,与上一时刻相比产生较大的角速度误差eω;在27 s时由于机器人运动状态的改变再一次产生较大的误差,因此机器人位姿的变化同时引起机器人角速度发生波动(图 19b)。
|
| 图 19 机器人行进中车轮线速度误差(a)和角速度误差(b)曲线 Fig.19 Error curves of wheel linear velocity (a) and angular velocity (b) in robot moving |
5 结论
针对脑卒中患者的术后下肢运动功能的康复训练,设计了一种可对患者移动陪护的康复机器人,并建立下肢康复机器人的运动学模型以及运动控制系统的Simulink模型,仿真验证了运动学模型的准确性。同时,研究构建了机器人平台上的人体姿态行为信息采集的传感器系统,提出基于模糊PID的人体姿态实时识别智能控制系统及控制算法。相较于经典PID,该算法可以实时调整PID的参数,以适应不同的使用情况,证明了该算法的有效性。此外,当输入相同设定速度时,通过对比经典PID与模糊PID发现后者具有较快的调节时间,稳定性也更好,调节精度更高,可以达到机器人稳定快速跟随人体运动的目的。最后通过实验测试发现,该下肢康复机器人使用模糊PID控制技术实现了智能同步运动的功能,具有响应速度快、反应时间短等优点。该机器人可以提高患者主动进行康复训练的积极性,加快患者的康复进程。
| [1] |
樊瑜波. 可穿戴医疗/健康技术: 生物医学工程的机遇和挑战[J]. 生物医学工程学杂志, 2016, 33(1): 1. |
| [2] |
余央央. 中国人口老龄化对医疗卫生支出的影响: 基于城乡差异的视角[D]. 上海: 复旦大学, 2012.
|
| [3] |
陈江芸. 健康老龄化背景下医养结合模式及老年人健康保障研究[D]. 武汉: 华中科技大学, 2019.
|
| [4] |
王芳, 林万隆, 叶斌, 等. 三级康复网络模式对脑卒中患者预后的影响[J]. 上海医药, 2021, 42(7): 17-20. DOI:10.3969/j.issn.1006-1533.2021.07.005 |
| [5] |
刘源, 朱怡婧, 金珑泽. 一种基于多传感器数据的人体行为监测及智能识别方法: 108446733A[P]. 2018-08-24[2021-06-25].
|
| [6] |
陈盛, 严以哲, 徐国政, 等. 面向肩关节自适应调节助力的镜像式主动康复训练[J]. 生物医学工程学杂志, 2021, 38(2): 351-360. |
| [7] |
蒋亚杰. 基于Kinect的人体姿态识别和机器人控制[D]. 深圳: 深圳大学, 2017.
|
| [8] |
唐彪, 樊启润, 孙开鑫, 等. 人体姿态识别算法在视觉人机交互中的应用[J]. 计算机测量与控制, 2019, 27(7): 242-247. |
| [9] |
BOŠNAK M, ŠKRJANC I. Embedded control system for smart walking assistance device[J]. IEEE Transactions on Neural Systems & Rehabilitation Engineering, 2016. DOI:10.1109/TNSRE.2016.2553369 |
| [10] |
HOMICH A J, DOERZBACHER M A, TSCHANTZ E L, et al. Minimizing human tracking error for robotic rehabilitation device[J]. Journal of Medical Devices, 2015, 9(4): 041003. DOI:10.1115/1.4030275 |
| [11] |
伊蕾, 张立勋, 于彦春. 助行康复机器人助力行走控制研究[J]. 华中科技大学学报: 自然科学版, 2014, 42(12): 41-46. |
| [12] |
马飞越, 周秀, 倪辉, 等. 基于区间二型模糊滑模的移动机器人轨迹跟踪控制[J]. 科学技术与工程, 2020, 20(30): 12472-12477. DOI:10.3969/j.issn.1671-1815.2020.30.031 |



