2. 北京理工大学机电学院, 北京 100081;
3. 广西科技大学电气与信息工程学院, 广西柳州 545006
2. School of Mechatronical Engineering, Beijing Institute of Technology, Beijing, 100081, China;
3. School of Electrical and Information Engineering, Guangxi University of Science and Technology, Liuzhou, Guangxi, 545006, China
随着人口老龄化现象愈来愈严重,康复医疗逐渐引起社会的广泛关注。目前我国从事康复事业的人员稀缺,部分患者由于不能及时得到科学有效的康复训练导致训练效果差,致残率高。国内康复产业缺口较大,相关产业相较于国外仍存在较大差距,康复设备种类较少,功能单一。
目前国际康复领域普遍认同的针对脊椎损伤患者有效的康复训练治疗手段是减重步行训练(Body Weight Supported Training, BWST)。下肢康复机器人可以通过减重单元实现可控减重,为患者提供更为安全的减重步行训练。正常人在行走过程中,重心离地高度为变化量,为使患者拥有更好的用户体验,减重步行训练过程中的减重力应满足:大小可控且在垂直地面方向具有一定自由移动距离的力。减重力可以随设备使用者重心离地高度变化而变化,减轻使用者不适感。
现有下肢康复设备多为固定式,而移动式下肢康复机器人能为穿戴者提供更接近真实行走的感受,移动式康复机器人对减重单元也提出了更高的要求。移动式康复机器人减重单元由弹簧、力臂板、丝杆滑轨以及电机相互协作实现减重效果。通过协调内部各个部件可以使减重单元结构更加紧凑,工作效率更高。由于减重单元内部为一个多因素多目标优化问题,使用传统的方法解耦难度大,而使用带精英策略的非支配排序遗传算法(NSGA-Ⅱ)可以较快地获得优化结果。如杨筱沛等[1]、王冬良等[2]通过NSGA-Ⅱ较好地优化了机构内的多目标问题。本研究在分析减重单元结构的基础上,拟通过建立以减小减重单元体积为目标的多目标优化模型,提高机构工作效率,使减重单元在工作过程中输出的力尽可能稳定。
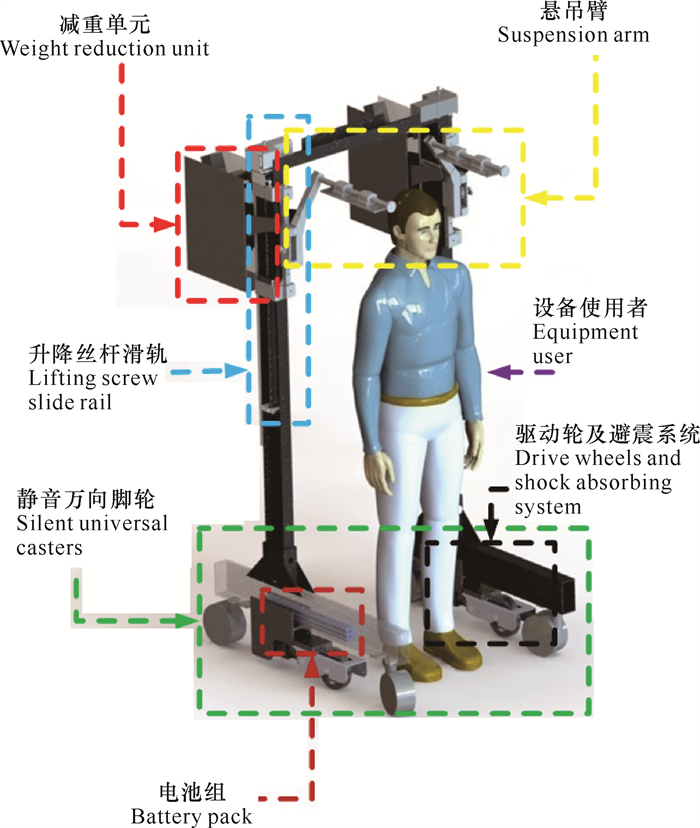
1 减重单元设计移动式下肢康复机器人的核心系统之一为减重单元。由图 1可知,机器人结构部分主要由龙门架框架、减重单元、悬吊臂、升降丝杆滑轨、驱动轮及避震系统以及电池组组成。其中设备使用者与悬吊臂通过穿戴减重康复训练服柔性固定,悬吊臂与减重单元内的输出力臂相连,由减重单元提供减重训练所需减重力,减重单元与升降丝杆滑轨相连,升降丝杆滑轨可以根据需求调节减重单元离地高度,以增加设备适用性。4个静音万向轮为机器人提供整体支撑力,驱动轮及避震系统为康复机器人提供整体移动所需动力,电池组提供机器人能源。
|
| 图 1 移动式下肢康复机器人结构设计 Fig.1 Structural design of mobile lower limb rehabilitation robot |
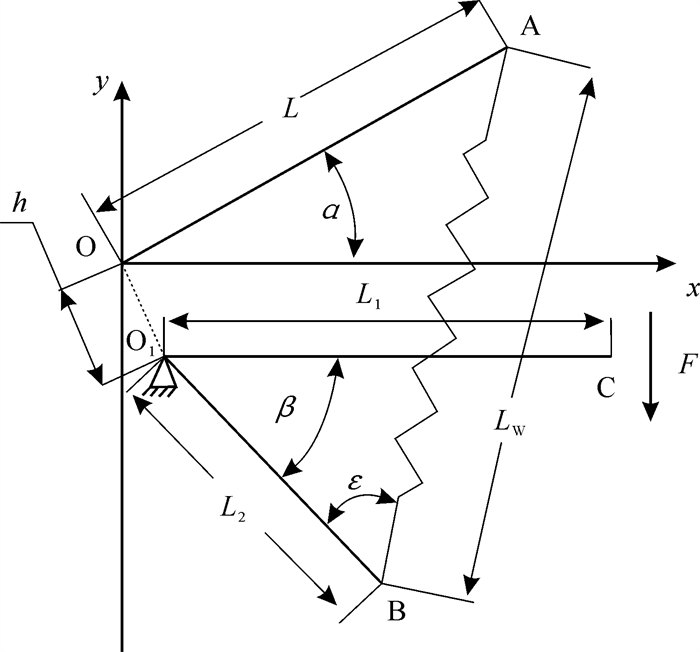
图 2为减重单元原理图。以滑轨起点O为原点,建立平面直角坐标系,OA为丝杆滑轨,L为丝杆滑轨中滑块移动的距离;α为滑轨与水平面的夹角;h为滑轨起点距离力臂旋转点O1的垂距;O1C为输出力臂,长度为L1;O1B为输入力臂,长度为L2;β为输入力臂与输出力臂之间的夹角;AB为拉簧,原长为L0,工作长度为LW;F为输出力[3]。
|
| 图 2 减重单元原理图 Fig.2 Schematic diagram of weight reduction unit |
2 减重单元多目标优化 2.1 多目标优化模型建立 2.1.1 确定设计变量
由原理图可知,该模型内,自由变量为L、L1、L2、α、β、h、k以及LW。其中,L通过电机控制丝杆滑轨上的滑块实现可控,通过控制L的长短实现输出力臂O1C输出力F的大小。k与LW为拉力弹簧的劲度系数与工作长度,为简化模型,通过测试实验确定弹簧的劲度系数k为8 N/mm。h为丝杆滑轨起点与三角力臂板CO1B的旋转中心O1的距离,该数值受丝杆滑轨外形参数影响,取定值100 mm。
2.1.2 目标函数在减重单元工作过程中,三角力臂板CO1B输出力臂O1C围绕O1点旋转,而输出力臂O1C与输入力臂O1B夹角β为力臂板的固有数值,在加工好后无法修改。为配合设备使用者在行走过程中重心离地的变化,输出力臂在设备工作中绕O1点旋转,C点通过转向装置连接悬吊臂,为悬吊臂提供所需输出减重力。当输出力臂O1C绕O1旋转时, 输入力臂O1B从动旋转,B点与A点之间连接弹簧,由于旋转输入力臂与弹簧的夹角ε会改变弹力以及弹簧的伸长量也会改变,该角度的改变影响拉力的转化率。优化减重单元使力臂板CO1B在绕O1旋转过程中C点输出力尽可能稳定为一常量。
AB是由弹簧相连,AB的长度L0或LW决定弹簧的输出力,由胡克定律可得:
| $ F = k\mathit{\Delta }L。$ | (1) |
式(1)中,F为弹簧输出力;k为弹簧劲度系数;ΔL为弹簧增长量,即ΔL=LW-L0,LW为弹簧工作长度,L0为弹簧原长。
再由力矩平衡原理:
| $ {F_1} \times {L_1} = {F_2} \times {L_2}。$ | (2) |
可以求得C端点输出力F。
代入上述数据可得:
| $ F = \frac{{{L_2}}}{{{L_1}}} \times k \times \left( {{L_{\rm{W}}} - {L_0}} \right) \times {\rm{sin \mathsf{ ε}}} 。$ | (3) |
式(3)中,ε为弹簧与输入力臂之间的夹角,可由平面向量夹角公式求得:
| $ {\rm{cos \mathsf{ ε} }} = {\rm{ }}\frac{{{\mathit{\boldsymbol{O}}_1}\mathit{\boldsymbol{B}} \times \mathit{\boldsymbol{AB}}}}{{|{\mathit{\boldsymbol{O}}_1}\mathit{\boldsymbol{B}}\left| \times \right|\mathit{\boldsymbol{AB}}|{\rm{ }}}}{\rm{ }}。$ | (4) |
为化简问题,在该模型中,使弹簧AB的长度变化尽可能小,可使得力臂O1C绕O1点转动过程中C点输出力F变化尽可能小,即有
| $ \begin{array}{l} {f_1}\left( {\beta , {L_2}} \right) = - |\Delta | = - |A{B_1} - A{B_2}| = \\ - \sqrt {{{\left( {{W_1}\left( {\beta - \frac{\pi }{6}, \beta } \right)} \right)}^2} + {{\left( {{W_2}\left( {\beta - \frac{\pi }{6}, \beta } \right)} \right)}^2}} + \\ \sqrt {{{\left( {{W_1}\left( {\beta + \frac{\pi }{6}, \beta } \right)} \right)}^2} + {{\left( {{W_2}\left( {\beta + \frac{\pi }{6}, \beta } \right)} \right)}^2}} , \end{array} $ | (5) |
| $ {W_1}\left( {a, b} \right) = h\;{\rm{sin}}\left( a \right) + {L_2}\;{\rm{cos}}\left( b \right) - L{\rm{cos}}\left( b \right), $ | (6) |
| $ {W_2}\left( {a, b} \right) = h{\rm{cos}}\left( a \right) + {L_2}{\rm{sin}}\left( b \right) + L{\rm{sin}}\left( b \right)。$ | (7) |
为提高减重单元的效率,减小减重单元整体体积为第二优化目标。计算式:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;{f_2}\left( {\alpha , \beta , {L_2}} \right) = \\ L{\rm{cos}}\alpha \times \left( {L{\rm{sin}}\alpha + h{\rm{cos}}\alpha + {L_2}{\rm{sin}}\beta } \right) \end{array}。$ | (8) |
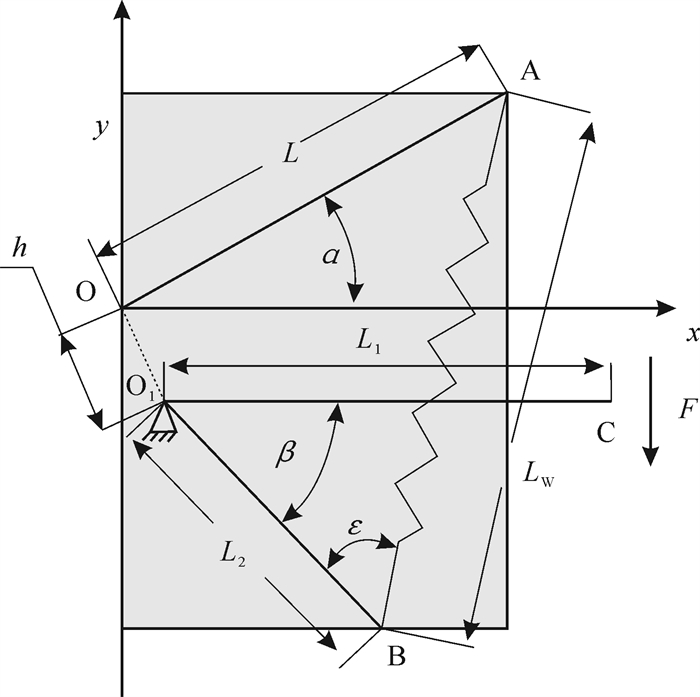
图 3为减重单元侧面积示意图。
|
| 图 3 减重单元侧面积示意图 Fig.3 Diagram of side area of weight reduction unit |
2.1.3 约束条件
根据减重单元设计要求,(单边减重单元)输出的力为F,且最大值大于250 N。即
| $ \begin{array}{l} F\left( {{L_1}, {L_2}, \alpha , \beta } \right) = k \times \frac{{{L_2}}}{{{L_1}}} \times \\ \left( {\sqrt {{U^2} + {V^2}} - {L_0}} \right) \times {\rm{sin}}\left( {{\rm{arccos}}\frac{{U{\rm{cos}}\beta + V{\rm{sin}}\beta }}{{\sqrt {{U^2} + {V^2}} }}} \right) \end{array}。$ | (9) |
其中:
| $ U\left( {\alpha , \beta , {L_2}} \right) = h \times {\rm{sin}}\alpha + {L_2} \times {\rm{cos}}\beta - L \times {\rm{cos}}\alpha , $ | (10) |
| $ V\left( {\alpha , \beta , {L_2}} \right) = L \times {\rm{sin}}\alpha + h \times {\rm{cos}}\alpha + {L_2} \times {\rm{sin}}\beta 。$ | (11) |
由于该问题具有实际意义,每个变量均有其取值范围(表 1)。
| 范围Range | 变量Variables | |||
| α (rad) |
β (rad) |
L1 (mm) |
L2 (mm) |
|
| 上限Upper limit | 1.57 | 1.57 | 350 | 350 |
| 下限Lower limit | 0 | 0 | 100 | 100 |
2.1.4 减重单元多目标优化模型
综上所述,减重单元多目标优化模型可表示为目标函数:
| $ \begin{array}{l} {f_1}\left( {\beta , {L_2}} \right) = - {\rm{|}}\Delta {\rm{|}} = - {\rm{|}}A{B_1} - A{B_2}{\rm{|}} = \\ - \sqrt {{{\left( {{W_1}\left( {\beta - \frac{\pi }{6}, \beta } \right)} \right)}^2} + {{\left( {{W_2}\left( {\beta - \frac{\pi }{6}, \beta } \right)} \right)}^2}} + \\ \sqrt {{{\left( {{W_1}\left( {\beta + \frac{\pi }{6}, \beta } \right)} \right)}^2} + {{\left( {{W_2}\left( {\beta + \frac{\pi }{6}, \beta } \right)} \right)}^2}} , \\ \begin{array}{*{20}{l}} {{W_1}\left( {a, b} \right) = h{\rm{sin}}\left( a \right) + {L_2}{\rm{cos}}\left( b \right){\rm{ - }}L{\rm{cos}}\left( b \right), }\\ {{W_2}\left( {a, b} \right) = h{\rm{cos}}\left( a \right) + {L_2}{\rm{sin}}\left( b \right) + L{\rm{sin}}\left( b \right)}。\end{array} \end{array} $ |
为配合整体求最小值,有
| $ \begin{array}{l} \;\;\;\;\;\;f{'_2}\left( {\alpha , \beta , {L_2}} \right) = - {f_2}\left( {\alpha , \beta , {L_2}} \right) = - L{\rm{cos}}\alpha \times \\ \left( {L{\rm{sin}}\alpha + h{\rm{cos}}\alpha + {L_2}{\rm{sin}}\beta } \right)。\end{array} $ | (12) |
减重值约束:
| $ \begin{array}{l} \;\;\;\;\;\;k \times \frac{{{L_2}}}{{{L_1}}} \times \left( {\sqrt {{U^2} + {V^2}} - {L_0}} \right) \times \\ {\rm{sin}}\left( {{\rm{arccos}}\frac{{U{\rm{cos}}\beta + V{\rm{sin}}\beta }}{{\sqrt {{U^2} + {V^2}} }}} \right) \ge 250, \end{array} $ | (13) |
其中, U, V分别由式(10)和(11)求得:
设计变量取值范围约束:
多目标优化问题(Multi-objective Optimization Problem, MOP)起源于许多实际复杂系统的设计、城市运输、资本预算等。这些现实问题在决策中都要考虑不同的约束条件,需要同时处理多个相冲突的目标,而这些多个优化目标并非独立存在,他们之间常常存在耦合关系,相互竞争,并且每个目标又具有不同的物理意义和量纲。21世纪,初遗传算法(Genetic Algorithm, GA)[4]逐渐成为多目标优化问题的研究热点,在标准遗传算法的基础上通过添加隔离小生境技术[5, 6]、动态调整距离参数等方式提出新的算法,使遗传算法在局部搜索能力、收敛能力等方面有明显提升[7, 8]。多目标优化算法NSGA-Ⅱ在搜索Pareto最优解集方面有良好表现[9]。多目标优化问题的Pareto最优解仅仅是一个可以接受的“不坏”的解,通常具有多个Pareto最优解。须针对问题从最优解集中挑选一部分解集作为问题的最优解[10]。
2.2.1 NSGA-Ⅱ算法改进变异运算是指将染色体编码串中某些基因座上的基因用其他的等位基因替换,从而使种群中产生新的个体。该变异属于辅助性操作,主要作用是提高种群内多样性的功能,从而提高遗传算法的全局搜索能力。如果变异概率太大,虽然能使群体中任意产生新的个体,但不易使群体收敛,并且后期容易破坏优秀的染色体。而变异概率太小又会使群体活力不足,从而陷入局部最优。本研究使用拟退火的思路,在此处添加一个活跃因子,在进化前期使种群具有足够的活力,在进化后期逐渐减小,达到快速收敛的效果。活跃因子与迭代次数成反比。一般变异概率Pm取值0.001至0.4。
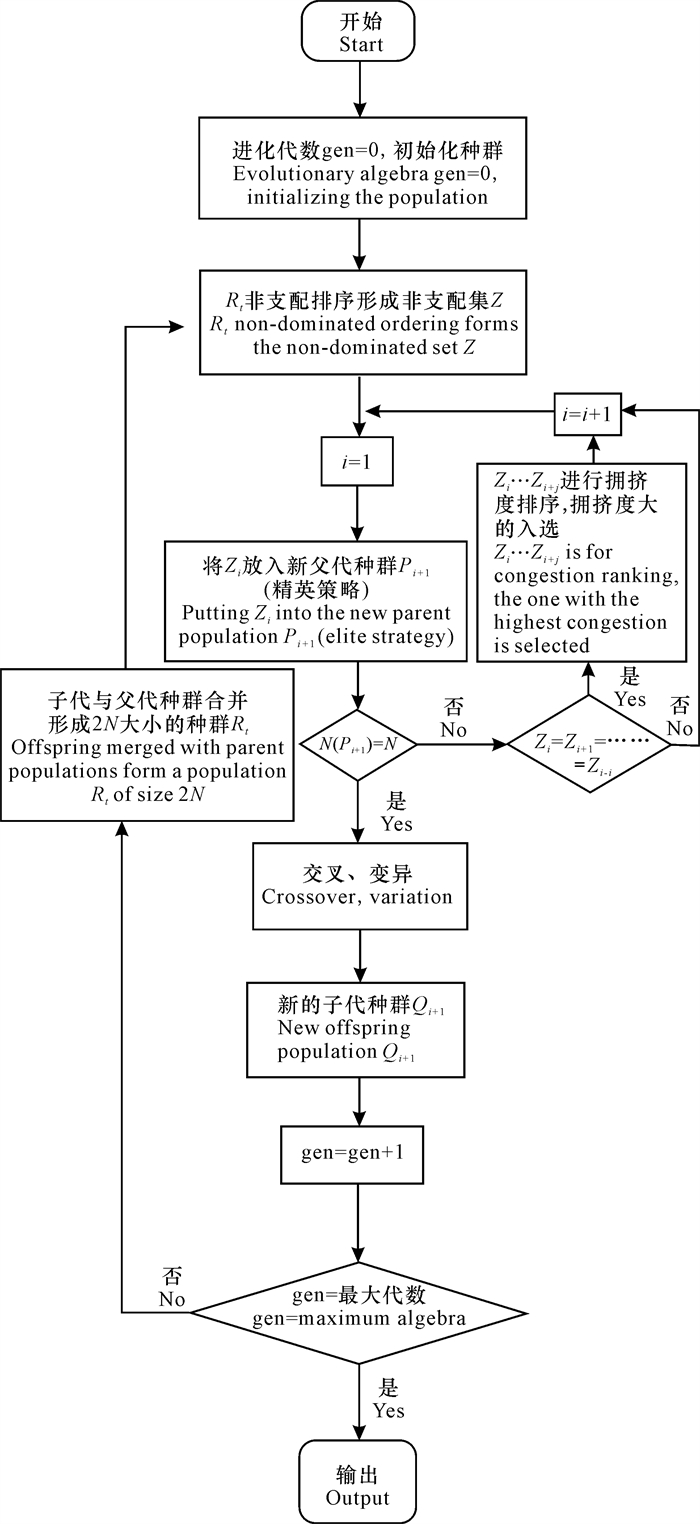
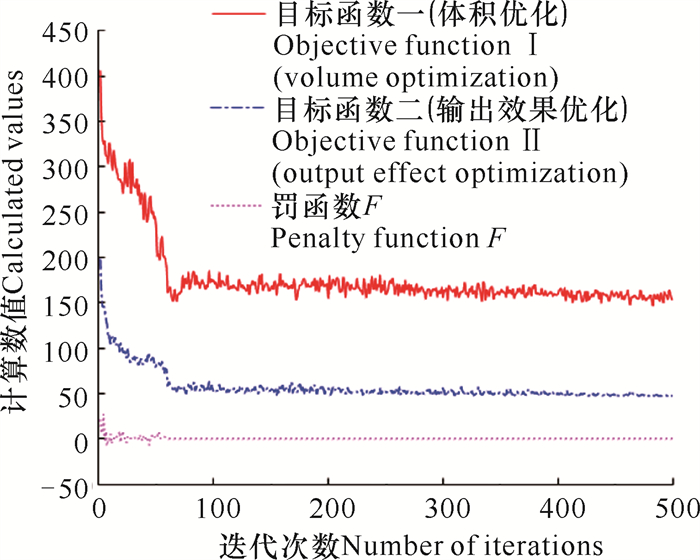
2.2.2 NSGA-Ⅱ算法仿真基于所建立减重单元模型,使用NSGA-Ⅱ算法,算法流程如图 4所示,通过经验设置算法参数(表 2),可获得减重单元Pareto前沿,如图 5所示。
|
| 图 4 NSGA-Ⅱ流程图 Fig.4 NSGA-Ⅱ flow chart |
| 参数Parameters | 设定值Setting value |
| 种群代数Population algebra | 100 |
| 迭代次数Number of iterations | 500 |
| 交叉概率Crossover probability | 0.90 |
| 变异概率Mutation probability | 0.400 0-0.000 8*gen |
|
| 图 5 迭代次数及函数对应关系 Fig.5 Number of iterations and function correspondence |
通过软件仿真获得Pareto解集,根据实际情况进行筛选,优化前后减重单元设计参数取值如表 3所示。由表 3可知,利用算法优化在降低输出减重力效果的前提下,减小了减重单元的体积,提高了设备的密度。
| 项目Item | 参数Parameters | |||||
| α (rad) |
β (rad) |
L1 (mm) |
L2 (mm) |
F(N) | 减重单元侧面积 Side area of weight reduction unit (S, mm2) |
|
| 优化前 Before optimization |
0.52 | 1.22 | 200 | 100 | 264 | 34 228.650 |
| 优化后 After optimization |
1.50 | 0.04 | 190 | 90 | 248 | 1 685.629 |
3 实验验证
为模拟各种减重单元的数据搭配,验证各种可能性,特设计如图 6所示实验机。该实验平台使用铝型材搭建,可以模拟弹簧盒减重单元内不同数据的组合。通过调整铝型材的相对位置来实现弹簧盒内不同数据的配合。通过组合实验获得实验数据,在每个变量可行域区间长度中,选取位于其15%、50%以及75%位置的量进行测试,共计81组实验。弹簧使用弹簧盒减重单元设置的拉力弹簧。通过拉力计测量输出力的大小并做记录,将优化前与优化后的数据一同代入对比,共计83组数据(表 4)。

|
| 图 6 减重单元实验机 Fig.6 Experimental machine of weight reduction unit |
| 编号 Number |
α (rad) |
β (rad) |
L1 (mm) |
L2(mm) | F (N) |
S (mm2) |
| 1 | 0.26 | 0.26 | 100.00 | 100.00 | 248 | 26 166.11 |
| 2 | 0.26 | 0.26 | 100.00 | 200.00 | ~ | ~ |
| 3 | 0.26 | 0.26 | 100.00 | 300.00 | ~ | ~ |
| 4 | 0.26 | 0.26 | 200.00 | 100.00 | 124 | 26 166.11 |
| 5 | 0.26 | 0.26 | 200.00 | 200.00 | 461 | 29 914.39 |
| 6 | 0.26 | 0.26 | 200.00 | 300.00 | ~ | ~ |
| 7 | 0.26 | 0.26 | 300.00 | 100.00 | 83 | 26 166.11 |
| 8 | 0.26 | 0.26 | 300.00 | 200.00 | 307 | 29 914.39 |
| 9 | 0.26 | 0.26 | 300.00 | 300.00 | 695 | 33 662.66 |
| 10 | 0.26 | 0.79 | 100.00 | 100.00 | 526 | 32 659.31 |
| 11 | 0.26 | 0.79 | 100.00 | 200.00 | ~ | ~ |
| 12 | 0.26 | 0.79 | 100.00 | 300.00 | ~ | ~ |
| 13 | 0.26 | 0.79 | 200.00 | 100.00 | 263 | 32 659.31 |
| 14 | 0.26 | 0.79 | 200.00 | 200.00 | 752 | 42 900.79 |
| 15 | 0.26 | 0.79 | 200.00 | 300.00 | ~ | ~ |
| 16 | 0.26 | 0.79 | 300.00 | 100.00 | 175 | 32 659.31 |
| 17 | 0.26 | 0.79 | 300.00 | 200.00 | 502 | 42 900.79 |
| 18 | 0.26 | 0.79 | 300.00 | 300.00 | ~ | ~ |
| 19 | 0.26 | 1.31 | 100.00 | 100.00 | 524 | 36 411.03 |
| 20 | 0.26 | 1.31 | 100.00 | 200.00 | ~ | ~ |
| 21 | 0.26 | 1.31 | 100.00 | 300.00 | ~ | ~ |
| 22 | 0.26 | 1.31 | 200.00 | 100.00 | 262 | 36 411.03 |
| 23 | 0.26 | 1.31 | 200.00 | 200.00 | ~ | ~ |
| 24 | 0.26 | 1.31 | 200.00 | 300.00 | ~ | ~ |
| 25 | 0.26 | 1.31 | 300.00 | 100.00 | 175 | 36 411.03 |
| 26 | 0.26 | 1.31 | 300.00 | 200.00 | ~ | ~ |
| 27 | 0.26 | 1.31 | 300.00 | 300.00 | ~ | ~ |
| 28 | 0.79 | 0.26 | 100.00 | 100.00 | 526 | 23 002.09 |
| 29 | 0.79 | 0.26 | 100.00 | 200.00 | ~ | ~ |
| 30 | 0.79 | 0.26 | 100.00 | 300.00 | ~ | ~ |
| 31 | 0.79 | 0.26 | 200.00 | 100.00 | 263 | 23 002.09 |
| 32 | 0.79 | 0.26 | 200.00 | 200.00 | 753 | 25 747.01 |
| 33 | 0.79 | 0.26 | 200.00 | 300.00 | ~ | ~ |
| 34 | 0.79 | 0.26 | 300.00 | 100.00 | 175 | 23 002.09 |
| 35 | 0.79 | 0.26 | 300.00 | 200.00 | 502 | 25 747.01 |
| 36 | 0.79 | 0.26 | 300.00 | 300.00 | ~ | ~ |
| 37 | 0.79 | 0.79 | 100.00 | 100.00 | 524 | 27 757.16 |
| 38 | 0.79 | 0.79 | 100.00 | 200.00 | ~ | ~ |
| 39 | 0.79 | 0.79 | 100.00 | 300.00 | ~ | ~ |
| 40 | 0.79 | 0.79 | 200.00 | 100.00 | 262 | 27 757.16 |
| 41 | 0.79 | 0.79 | 200.00 | 200.00 | 690 | 35 257.16 |
| 42 | 0.79 | 0.79 | 200.00 | 300.00 | ~ | ~ |
| 43 | 0.79 | 0.79 | 300.00 | 100.00 | 175 | 27 757.16 |
| 44 | 0.79 | 0.79 | 300.00 | 200.00 | ~ | ~ |
| 45 | 0.79 | 0.79 | 300.00 | 300.00 | ~ | ~ |
| 46 | 0.79 | 1.31 | 100.00 | 100.00 | 267 | 30 504.61 |
| 47 | 0.79 | 1.31 | 100.00 | 200.00 | ~ | ~ |
| 48 | 0.79 | 1.31 | 100.00 | 300.00 | ~ | ~ |
| 49 | 0.79 | 1.31 | 200.00 | 100.00 | 134 | 30 504.61 |
| 50 | 0.79 | 1.31 | 200.00 | 200.00 | ~ | ~ |
| 51 | 0.79 | 1.31 | 200.00 | 300.00 | ~ | ~ |
| 52 | 0.79 | 1.31 | 300.00 | 100.00 | 89 | 30 504.61 |
| 53 | 0.79 | 1.31 | 300.00 | 200.00 | ~ | ~ |
| 54 | 0.79 | 1.31 | 300.00 | 300.00 | ~ | ~ |
| 55 | 1.31 | 0.26 | 100.00 | 100.00 | 524 | 7 856.48 |
| 56 | 1.31 | 0.26 | 100.00 | 200.00 | ~ | ~ |
| 57 | 1.31 | 0.26 | 100.00 | 300.00 | ~ | ~ |
| 58 | 1.31 | 0.26 | 200.00 | 100.00 | 262 | 7 856.48 |
| 59 | 1.31 | 0.26 | 200.00 | 200.00 | ~ | ~ |
| 60 | 1.31 | 0.26 | 200.00 | 300.00 | ~ | ~ |
| 61 | 1.31 | 0.26 | 300.00 | 100.00 | 175 | 7 856.48 |
| 62 | 1.31 | 0.26 | 300.00 | 200.00 | ~ | ~ |
| 63 | 1.31 | 0.26 | 300.00 | 300.00 | ~ | ~ |
| 64 | 1.31 | 0.79 | 100.00 | 100.00 | 267 | 9 600.57 |
| 65 | 1.31 | 0.79 | 100.00 | 200.00 | ~ | ~ |
| 66 | 1.31 | 0.79 | 100.00 | 300.00 | ~ | ~ |
| 67 | 1.31 | 0.79 | 200.00 | 100.00 | 134 | 9 600.57 |
| 68 | 1.31 | 0.79 | 200.00 | 200.00 | ~ | ~ |
| 69 | 1.31 | 0.79 | 200.00 | 300.00 | ~ | ~ |
| 70 | 1.31 | 0.79 | 300.00 | 100.00 | 89 | 9 600.57 |
| 71 | 1.31 | 0.79 | 300.00 | 200.00 | ~ | ~ |
| 72 | 1.31 | 0.79 | 300.00 | 300.00 | ~ | ~ |
| 73 | 1.31 | 1.31 | 100.00 | 100.00 | ~ | ~ |
| 74 | 1.31 | 1.31 | 100.00 | 200.00 | ~ | ~ |
| 75 | 1.31 | 1.31 | 100.00 | 300.00 | ~ | ~ |
| 76 | 1.31 | 1.31 | 200.00 | 100.00 | ~ | ~ |
| 77 | 1.31 | 1.31 | 200.00 | 200.00 | ~ | ~ |
| 78 | 1.31 | 1.31 | 200.00 | 300.00 | ~ | ~ |
| 79 | 1.31 | 1.31 | 300.00 | 100.00 | ~ | ~ |
| 80 | 1.31 | 1.31 | 300.00 | 200.00 | ~ | ~ |
| 81 | 1.31 | 1.31 | 300.00 | 300.00 | ~ | ~ |
| 82 | 0.52 | 1.22 | 200.00 | 100.00 | 231 | 35 450.02 |
| 83 | 1.52 | 0.03 | 190.00 | 90.00 | 240 | 1 268.94 |
| 注:“~”表示无效的数据,导致其无效的原因有弹簧拉伸量超过弹簧许用拉伸长度、输出力臂过短模型无法成立等 Note: "~" indicates invalid data, the reasons for invalid data are that the spring extension exceeds the allowable spring extension length, the output force arm is too short for the model to be valid, etc | ||||||
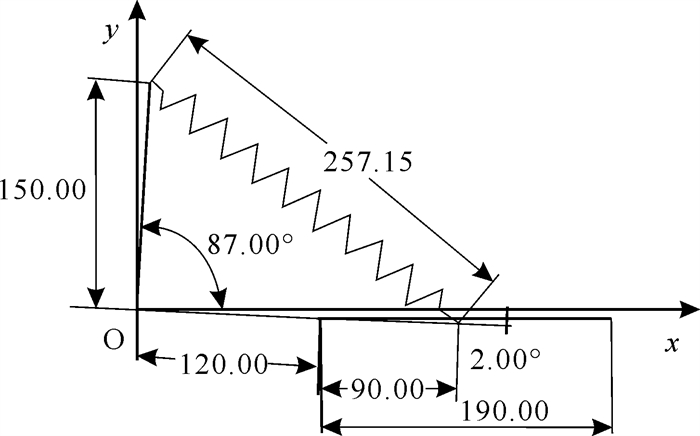
通过观察1-81组实验数据可以发现,在角α趋向于1.57、角β趋向于0时,减重单元的侧面积在实验组内最小,故优化的结果极大可能在该区域内。从表 4也可以看出,L1与减重单元的侧面积无相关性。通过仿真及验证获得减重单元原理图(图 7),即为满足多目标优化后的原理图。
|
| 图 7 优化后减重单元原理图 Fig.7 Optimized weight reduction unit schematic |
4 结论
本研究设计了移动式下肢康复机器人结构,并且深入研究减重单元,确定了减重单元内各个变量的取值范围,为后续优化设计奠定了基础。分析了减重单元各个变量间的关系,以提高减重单元工作效率及输出效果为设计优化目标,引入输出效果力为约束条件,建立减重单元的多目标优化模型;使用带精英策略的非支配排序遗传算法(NSGA-Ⅱ)进行优化求解,获得Pareto最优解集,根据实际工况,通过筛选获得优化结果。设计实验验证该模型中获得的优化结果在最优解域内。通过优化,减小了移动式下肢康复机器人内减重单元的体积,使结构更科学合理。
本研究应用启发式算法解决在实际机械设计过程中的多目标问题,证实了算法的有效性,在算法运行后尽量提出种群中不合理解,更有效地指导算法决策者向偏好的方向搜索,提高设计效率。后续工作可以考虑对机械工作原理与实现方式进行优化。
| [1] |
杨筱沛, 王威, 蒋博彦, 等. 基于NSGA-Ⅱ算法的二维翼型凹槽结构优化[J]. 工程热物理学报, 2019, 40(4): 804-807. |
| [2] |
王冬良, 陈南, 秦洪艳. 电动汽车轮毂电机-多连杆悬架系统设计与优化[J]. 机械设计与制造, 2020(5): 224-227. DOI:10.3969/j.issn.1001-3997.2020.05.054 |
| [3] |
LIU H, LI J, WANG S G, et al. Research on genetic algorithm of mechanical structure optimization of weight reduction system[C]//2020 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China: IEEE, 2020: 171-175.
|
| [4] |
HOLLAND J H. Adaptation in natural and artificial systems: An introductory analysis with applications to biology, control, and artificial intelligence[M]. Cambridge: MIT Press, 1992.
|
| [5] |
林焰, 郝聚民, 纪卓尚, 等. 隔离小生境遗传算法研究[J]. 系统工程学报, 2000, 15(1): 86-91. DOI:10.3969/j.issn.1000-5781.2000.01.014 |
| [6] |
TAZAWA I, KOAKUTSU S, HIRATA H. An evolutionary optimization based on the immune system and its application to the VLSL floor-plan design problem[J]. Electrical Engineering in Japan, 1998, 124(4): 27-36. DOI:10.1002/(SICI)1520-6416(199809)124:4<27::AID-EEJ4>3.0.CO;2-M |
| [7] |
周北岳, 邓斌, 郭观七. 基于小生境技术的改进遗传算法研究[J]. 机械强度, 2002, 24(1): 13-16, 103. DOI:10.3321/j.issn:1001-9669.2002.01.004 |
| [8] |
喻寿益, 郭观七. 一种改善遗传算法全局搜索性能的小生境技术[J]. 信息与控制, 2001, 30(6): 526-530, 542. DOI:10.3969/j.issn.1002-0411.2001.06.010 |
| [9] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transaction on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [10] |
孟红云. 多目标进化算法及其应用研究[D]. 西安: 西安电子科技大学, 2005: 10.
|



