2. 北京理工大学机电学院, 北京 100081;
3. 广西科技大学机械与汽车工程学院, 广西柳州 545616
2. School of Mechatronical Engineering, Beijing Institute of Technology, Beijing, 100081, China;
3. School of Mechanical and Automotive Engineering, Guangxi University of Science and Technology, Liuzhou, Guangxi, 545616, China
在各种灾害中,火灾不仅毁坏物质财产,造成社会秩序混乱,而且还直接或间接危害生命,及时发现火情并采取相应措施可以有效降低火灾带来的损失。火灾的主要特点有温度高、烟雾浓、火势猛和蔓延快。为及时监测火情的发生,监测数据的传感器需要具有很高的灵敏度和准确性。当前应用在监测火情上的传感器存在安装位置固定、测量范围有限等方面的局限性。将火灾监测传感器安装在移动机器人上,可以有效解决上述局限性,实现火灾监测的无人化与准确化。
由于存在滑动、干扰、传感器误差等影响,轮式移动机器人在设定好的路径上进行巡检移动的过程中,跟踪误差不可避免[1]。针对轨迹跟踪控制问题,国内外学者进行大量的研究。Kanayama等[2]基于非完整移动机器人模型对系统的微分方程进行线性处理,并针对滑移问题引入速度/加速度限制。曹锦波等[3]基于机器人因外部扰动和建模不准确等造成的位姿误差问题,用改进型非线性扰动观测器对扰动进行估计,并用滑膜控制器对扰动进行补偿。李卫兵和吴琼[4]通过机器人运动学模型,推导轨迹跟踪误差表达式,借助误差表达式设计虚拟速度控制律,将该控制律作为机器人动力学模型的输入,控制机器人的力矩输出,达到实际轨迹可以很好地跟踪期望轨迹的预期。Zhang等[5]针对具有通信约束的非线性多智能体系统,采用分布式控制结构中的“leader-follower”模式,设计分布式自适应反步控制协同跟踪运动目标。Yousuf等[6]对一个多用途机器人动力学控制器采用Proportion Integral Differential (PID) 和反步控制器结合的方式,可以有效地限制超调量并提高瞬态反应时间。宋立业、邢飞[7]和尤波等[8]分别将自适应神经滑膜和模糊滑膜控制引入到非完整移动机器人的轨迹跟踪上。吴运雄和曾碧[9]将卷积神经与强化学习结合在一起,解决了传统算法存在的局部最优问题。姜烽等[10]将差分进化遗传算法与PID结合构建轨迹跟踪控制器,提高了轨迹跟踪的精度。沈智鹏和张晓玲[11]提出一种解决在跟踪过程中速度跳变的扰动补偿模糊自适应反演控制方法。崔明月等[12]将打滑程度用未知参数表示,设计一种补偿纵向滑差的自适应非线性控制律,并提出一种通过极点布置在线调整控制器增益的方法。目前的研究主要考虑运动控制算法在仿真方面的改进与优化,但未真正运用到实际的场景中。为此,本文将从实际出发,提出火灾预警巡检机器人在目标轨迹跟踪过程中的跟踪控制。首先根据火灾预警巡检机器人建立运动学模型,并依据该模型推导出跟踪误差方程,建立跟踪控制器,在控制器中引入虚拟反馈控制量,利用Lyapunov稳定性理论判断控制器的稳定性,最后借助仿真实验和实物验证算法的有效性。
1 火灾预警巡检机器人的系统框架火灾预警巡检机器人系统主要由3个部分组成:
① 环境感知。涉及多种传感器,包括烟雾、火焰、测距和温度检测传感器等,在巡检过程中实现对无人化仓库烟雾和温度的实时监测。
② 执行机构。为了方便后期的机器人维护,上层控制器部分与底层执行机构部分采用模块化设计,执行机构部分采用Arduino作为底层处理器,主要控制机器人底层电机的驱动。针对环境感知系统中存在的导航、传感器数据复杂和信息量较大等问题,上层控制器的处理器采用树莓派作为主控。
③ 通信模块。传感器将检测到的数据通过协议的方式传递给树莓派,执行机构部分与树莓派之间、导航与树莓派之间采用USB通信方式,为了方便管理者在后端管理平台查看机器人的位置和无人化仓库的情况,机器人平台与终端采用无线的方式实现通信。
为了能够让机器人按照一定的路径进行火灾监测,需规划出机器人从此刻位置到某一位置的移动路径,使得机器人从当前位姿到达目标位姿。移动机器人的速度与位置、位姿存在紧密联系,要对机器人进行控制,需要对其位姿进行准确表达。首先建立合适的坐标系,对主要信息量进行表达,然后分析各坐标系之间存在的位置关系,最后确定速度与位姿之间的数学关系表达式。火灾预警巡检机器人的系统整体框架如图 1所示。

|
| 图 1 火灾预警巡检机器人系统整体框架 Fig.1 Overall framework of fire warning and inspection robot system |
1.1 火灾预警巡检机器人运动学模型
机器人位姿如图 2所示,机器人的运动主要由底层电机负责。向量(x,y,θ)表示巡检机器人中心点P在全局坐标系{O,X,Y}中的位姿,x,y分别代表横、纵坐标,θ代表方向角,若θ为顺时针指向全局坐标轴X轴,表示为正,否则为负。轮间距为2b,轮直径为2r。(XC,YC)代表机器人局部坐标系,巡检机器人局部坐标系的运行速度为v,(

|
| 图 2 火灾预警巡检机器人位姿图 Fig.2 Position map of fire warning and inspection robot |
图 2所示的巡检机器人需满足纯滚动和无滑动情况,即
| $ \left[\begin{array}{l} \dot{x} \\ \dot{y} \end{array}\right]=\left[\begin{array}{l} v \cos \theta \\ v \sin \theta \end{array}\right] 。$ | (1) |
化简后得到移动机器人的约束方程:
| $ \dot{x} \sin \theta-\dot{y} \cos \theta=0 \text { 。} $ | (2) |
将巡检机器人局部坐标系的运行速度v转换为全局坐标系下的速度
| $ \dot{q}_{c}=S(q) v(t)=\left[\begin{array}{c} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{array}\right]=\left[\begin{array}{cc} \cos \theta & 0 \\ \sin \theta & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{c} v \\ \omega \end{array}\right], $ | (3) |
其中S(q)是一个雅可比矩阵,w表示巡检机器人的角速度,则运动学方程可表示为
| $ \left[\begin{array}{c} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{array}\right]=\left[\begin{array}{cc} \cos \theta & 0 \\ \sin \theta & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} v \\ \omega \end{array}\right] 。$ | (4) |
巡检机器人平台几何中心P的线速度v和角速度w与左右轮驱动角速度wR和wL的关系如式(5)和式(6)所示:
| $ v=\frac{r}{2}\left(\omega_{R}+\omega_{L}\right), $ | (5) |
| $ \omega=\frac{\omega_{R} r-\omega_{L} r}{2 b}, $ | (6) |
式(5)、式(6)中r为车轮的半径,将式(5)、式(6)用矩阵表示,如式(7)所示:
| $ \left[\begin{array}{c} v \\ \omega \end{array}\right]=\left[\begin{array}{cc} \frac{r}{2} & \frac{r}{2} \\ \frac{r}{2 b} & -\frac{r}{2 b} \end{array}\right]\left[\begin{array}{c} \omega_{R} \\ \omega_{L} \end{array}\right] 。$ | (7) |
巡检机器人的运动学方程改写为式(8)中:
| $ \left[\begin{array}{c} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{array}\right]=\left[\begin{array}{cc} \frac{r}{2} \cos \theta & \frac{r}{2} \cos \theta \\ \frac{r}{2} \sin \theta & \frac{r}{2} \sin \theta \\ \frac{r}{2 b} & -\frac{r}{2 b} \end{array}\right]\left[\begin{array}{c} \omega_{R} \\ \omega_{L} \end{array}\right] \text { 。} $ | (8) |
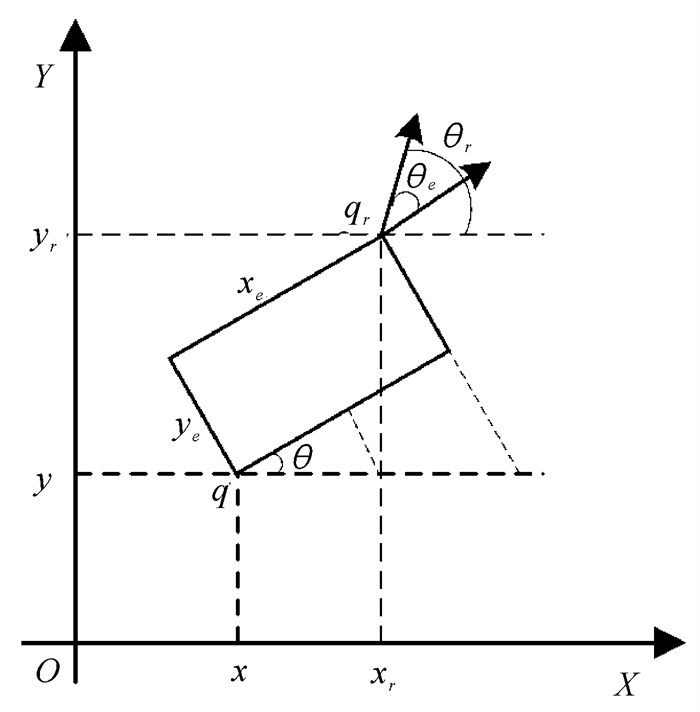
在轨迹跟踪过程中,需要将机器人期望的运动位姿与实际的位姿进行比较,计算并修正偏差。在图 3误差示意图中,qr表示巡检机器人的期望位姿,q表示巡检机器人的实际位姿。
|
| 图 3 火灾预警巡检机器人轨迹跟踪误差示意图 Fig.3 Schematic diagram of fire warning and inspection robot trajectory tracking error |
由图 3可知,非完整巡检机器人系统位姿跟踪误差方程如式(9)-(11):
| $ x_{e}=\left(x_{r}-x\right) \cos \theta+\left(y_{r}-y\right) \sin \theta, $ | (9) |
| $ y_{e}=\left(y_{r}-y\right) \cos \theta-\left(x_{r}-x\right) \sin \theta, $ | (10) |
| $ \theta_{e}=\theta_{r}-\theta, $ | (11) |
式(9)-(11)中xe为x方向的误差,ye为y方向的误差,θe为角度方向的误差, (xr, yr, θr)代表巡检机器人在x轴、y轴、角度方向的期望值。将式(9)-(11)写成矩阵形式,如式(12)所示:
| $ \begin{aligned} &\ \ \ \ \ \ \ \ e=\left[\begin{array}{l} x_{e} \\ y_{e} \\ \theta_{e} \end{array}\right]=\left[\begin{array}{ccc} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{c} x_{r}-x \\ y_{r}-y \\ \theta_{r}-\theta \end{array}\right]= \\ &T_{e}\left(q_{r}-q\right), \end{aligned} $ | (12) |
式(12)中
下面推导位姿误差微分方程,对式(9)进行求微分,可得式(13):
| $ \begin{aligned} &\dot{x}_{e}=-\dot{\theta} \sin \theta\left(x_{r}-x\right)+\cos \theta\left(\dot{x}_{r}-\dot{x}\right)+ \\ \dot{\theta} \cos \theta&\left(y_{r}-y\right)+\sin \theta\left(\dot{y}_{r}-\dot{y}\right)=\omega y_{e}-v+v_{r} \cos \theta_{e}。\end{aligned} $ | (13) |
对式(10)进行求微分,可得式(14):
| $ \begin{aligned} &\dot{y}_{e}=-\dot{\theta} \cos \theta\left(x_{r}-x\right)-\sin \theta\left(\dot{x}_{r}-\dot{x}\right)- \\ \dot{\theta} \sin \theta&\left(y_{r}-y\right)+\cos \theta\left(\dot{y}_{r}-\dot{y}\right)=-\omega x_{e}+v_{r} \sin \theta_{e}。\end{aligned} $ | (14) |
对式(11)进行求微分,可得式(15):
| $ \dot{\theta}_{e}=\dot{\theta}_{r}-\dot{\theta}=\omega_{r}-\omega。$ | (15) |
对式(13)-(15)进行整理,得到非完整巡检机器人系统的误差微分方程:
| $ \left[\begin{array}{c} \dot{x}_{e} \\ \dot{y}_{e} \\ \dot{\theta}_{e} \end{array}\right]=\left[\begin{array}{c} \omega y_{e}-v+v_{r} \cos \theta_{e} \\ -\omega x_{e}+v_{r} \sin \theta_{e} \\ \omega_{r}-\omega \end{array}\right]。$ | (16) |
根据位姿误差的微分方程,即式(16)设计合适的控制律,使机器人在轨迹跟踪过程中可以按照预定的轨迹运行,或者在出现误差时快速消除偏差。轨迹跟踪控制的目标就是设计合适的控制器v、w,使得跟踪误差趋于0:
| $ \lim\limits_{t \rightarrow \infty}\left[\left|x_{r}-r\right|+\left|y_{r}-y\right|+\left|\theta_{r}-\theta\right|\right]=0 \text { 。} $ |
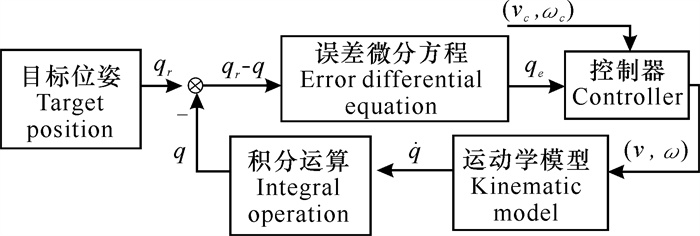
机器人轨迹跟踪流程如图 4所示。将期望位姿qr和实际位姿q进行对比,作为误差微分方程的输入,得到误差微分方程的输出,即位姿误差qe;位姿误差qe和期望速度(vc, wc)作为控制器的输入,得到控制器的输出,即控制速度(v, w);机器人的实际位姿q是将控制速度(v, w)作为运动学模型的输入,再经过积分运算得到的。
|
| 图 4 火灾预警巡检机器人轨迹跟踪流程 Fig.4 Frajectory tracking process of fire warning and inspection robot |
2.1 虚拟反馈量的设计
为找到合适的虚拟状态反馈函数xed,使得ye→0。借鉴文献[13-15]的思想,设xe为虚拟控制输入,设计控制量v和w使得xe→xed,θe→0,且整个系统渐进稳定。定义误差变量如式(17):
| $ \bar{x}_{e}=x_{e}-\frac{k_{1} y_{e}}{\sqrt{1+\omega^{2}}}, $ | (17) |
式(17)中,k1为增益系数,k1>0。根据式(17)可得到:当
选用一个局部Lyapunov函数V1:
| $ V_{1}=\frac{1}{2} y_{e}^{2}, $ | (18) |
对式(18)进行求导:
| $ \dot{V}_{1}=-\frac{k_{1} \omega y_{e}^{2}}{\sqrt{1+\omega^{2}}} \leqslant 0, $ | (19) |
在θe→0时,V1单调递减,并且可以使得ye收敛到0。
2.2 基于Lyapunov稳定性分析基于李雅普诺夫稳定性准则,构造全局Lyapunov函数V如式(20):
| $ V=\frac{1}{2} \bar{x}_{e}^{2}+\frac{1}{2} y_{e}^{2}+\frac{1-\cos \theta_{e}}{k_{y}}, $ | (20) |
式(20)中,ky为增益系数,ky>0,V>0,仅当(xe, ye, θe)T=0,V=0。
由式(16)和式(17)可得:
| $ \dot{\bar{x}}_{e}=\dot{x}_{e}-\frac{k_{1} \dot{y}_{e}}{\left(1+\omega^{2}\right)^{\frac{1}{2}}}+\frac{k_{1} y_{e} \omega \dot{\omega}}{\left(1+\omega^{2}\right)^{\frac{3}{2}}} 。$ | (21) |
同时对Lyapunov函数V求导得式(22):
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \dot{V}=\bar{x}_{e} \dot{\bar{x}}_{e}+y_{e} \dot{y}_{e}+\frac{1}{k_{y}} \sin \theta_{e} \dot{\theta}_{e}=\bar{x}_{e} \cdot \\ \left(\omega y_{e}-v+v_{r} \cos \theta_{e}-\frac{k_{1} \dot{y}_{e}}{\left(1+\omega^{2}\right)^{\frac{1}{2}}}+\frac{k_{1} y_{e} \omega \dot{\omega}}{\left(1+\omega^{2}\right)^{\frac{3}{2}}}\right)-\\ \frac{k_{1} y_{e}^{2} \omega}{\sqrt{1+\omega^{2}}}+\frac{1}{k_{y}} \sin \theta_{e}\left(\omega_{r}-\omega+2 k_{y} y_{e} v_{r}\right) 。\end{array} $ | (22) |
取系统的控制律为式(23):
| $ \left\{\begin{array}{l} \omega=\omega_{r}+2 k_{y} y_{e} v_{r}+k_{3} \sin \theta_{e} \\ v=\omega y_{e}+v_{r} \cos \theta_{e}-\frac{k_{1} \dot{y}_{e}}{\left(1+\omega^{2}\right)^{\frac{1}{2}}}+\frac{k_{1} y_{e} \omega \dot{\omega}}{\left(1+\omega^{2}\right)^{\frac{3}{2}}}+k_{2} \bar{x}_{e} \end{array},\right. $ | (23) |
式(23)中,k1,k2,k3,ky均为大于0的数,则
| $ \dot{V}=-k_{2} \bar{x}_{e}^{2}-\frac{k_{1} \omega y_{e}^{2}}{\sqrt{1+\omega^{2}}}-\frac{k_{3}}{k_{y}} \sin ^{2} \theta_{e} 。$ | (24) |
由于V为有界连续正定可微的函数,
为验证本文控制器的控制效果,通过Matlab对机器人系统进行经典控制器和本文控制器的仿真对比。经典控制器如式(25)所示:
| $ \left\{\begin{array}{l} v=v_{r} \cos \theta_{r}+k_{11} x_{e} \\ w=w_{r}+k_{22} v_{r} y_{e}+k_{33} v_{r} \sin \theta_{e} \end{array}\right., $ | (25) |
式(25)中,k11,k22,k33均为增益系数且大于0。
3.1 直线轨迹跟踪仿真仿真的参数设定如下,期望的角速度和线速度分别为wr=0 rad/s,vr=0.8 m/s,初始角速度和线速度分别为w=0.3 rad/s,v=0.4 m/s,初始位姿为[1.2 0 π/2],轨迹跟踪的参考位姿
qr = (xr yr θr )T 为
| $ \left\{\begin{array}{l} x_{r}=v_{r} \cos \left(\theta_{r} t\right) \\ y_{r}=v_{r} \sin \left(\theta_{r} t\right) \\ \theta_{r}=\pi / 3 \end{array}\right., $ | (26) |
其中,0≤t≤100;参数值:k1=1,k2=4.5,k3=4,ky=5,k11=8,k22=3,k33=3。仿真结果如图 5所示。
|
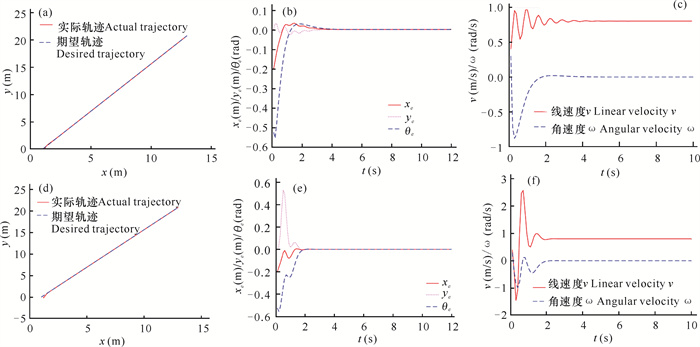
| 图 5 经典控制器(a-c)和本文控制器(d-f)直线轨迹跟踪仿真图 Fig.5 Simulation diagram of linear trajectory tracking for the classical controller (a-c) and the controller (d-f) in this article |
从图 5可以看出,机器人在经典控制器与本文控制器在初始值相同的跟踪过程中,都与目标轨迹重合。对比x轴方向的偏差、y轴方向的偏差和航向角θ的偏差可以看出,本文控制器存在较大的波动但提高了跟踪的收敛速度,本文控制器在3 s左右误差趋于0,经典控制器在5 s左右趋于0。
3.2 圆形轨迹跟踪仿真的参数设定如下,取轨迹跟踪过程中的期望角速度和线速度分别为wr=1 rad/s,vr=1 m/s,初始角速度和线速度分别为w=0.3 rad/s,v=0.4 m/s。初始位姿为[1.2 0 2π/3],轨迹跟踪的参考位姿qr=(xr yr θr)T为
| $ \left\{\begin{array}{l} x_{r}=v_{r} \cos \left(\theta_{r} t\right) \\ y_{r}=v_{r} \sin \left(\theta_{r} t\right) \\ \theta_{r}=w_{r} t \end{array}\right., $ | (27) |
其中,0≤t≤300,跟踪轨迹为圆心位于原点、半径为1的圆形;参数值:k1=1,k2=4,k3=5,ky=4,k11=3,k22=3,k33=2。仿真结果如图 6所示。
|
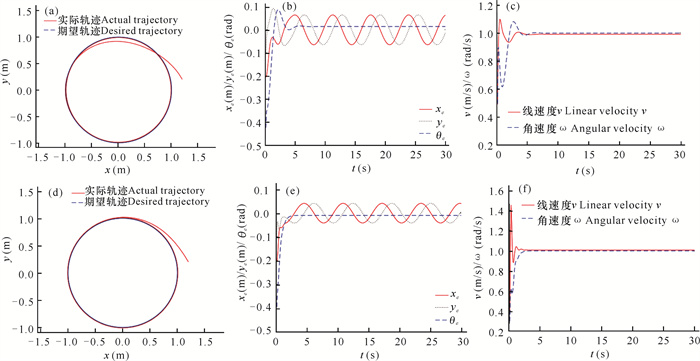
| 图 6 经典控制器(a-c)和本文控制器(d-f)圆形轨迹跟踪仿真图 Fig.6 Simulation diagram of circular trajectory tracking for the classical controller (a-c) and the controller (d-f) in this article |
从图 6可以看出,两种控制器在圆形轨迹跟踪上可以重合。对比两种控制器的误差图,可以看出本文控制器的误差波动比经典控制器的误差波动小,本文控制器角度误差5 s左右趋于0,经典控制器角度误差8 s左右趋于0。对比两种控制器的速度曲线,可以看出本文控制器在4 s左右达到稳定状态,经典控制器在7 s左右达到稳定状态。
3.3 实物验证为进一步验证轨迹跟踪控制器的正确性和有效性,进行巡检机器人的实物实验。参考轨迹可以用公式(28)表示:
| $ \left\{\begin{array}{l} x_{t}=x_{i}+v_{r} t \cos \theta \\ y_{t}=y_{i}+v_{r} t \sin \theta \\ \theta=\arctan \left[\left(y_{i}-y_{i-1}\right) /\left(x_{i}-x_{i-1}\right)\right] \end{array}\right.。$ | (28) |
实验环境包括一台巡检机器人,一个OpenMV摄像头,一台PC主机。PC主机采用无线形式与巡检机器人进行通信,巡检机器人将自身位置实时发送给PC机,PC机通过ROS平台将机器人反馈的数据录制下来并保存成.txt文件形式,在Matlab中绘制出实际与期望轨迹。
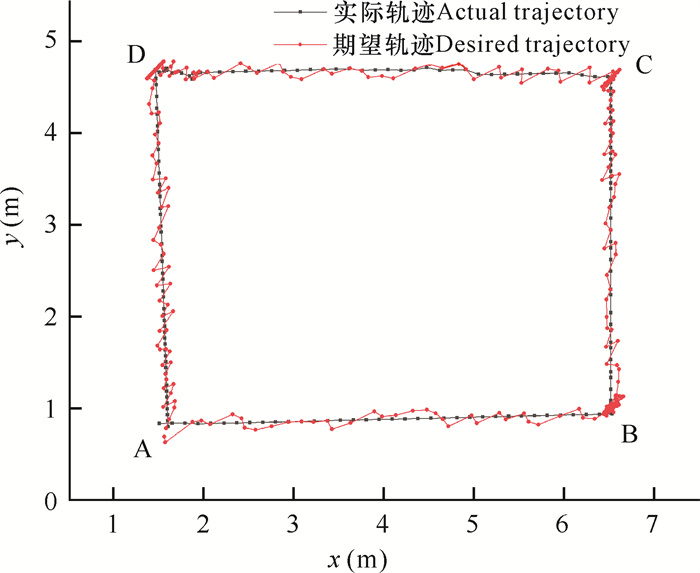
巡检机器人跟踪轨迹如图 7所示,机器人从A点(1.5,0.6)沿直线到B点(6.5,1),从B点沿直线到C点(6.5,4.8),从C点沿直线到D点(1.5,4.8),从D点沿直线到A点。图 8为机器人在运动过程中的位姿误差、角速度和线速度控制律,图 9为机器人的实物图。
|
| 图 7 巡检机器人运动轨迹图 Fig.7 Moving trajectory map of inspection robot |

|
| 图 8 巡检机器人实验数据 Fig.8 Experimental data of inspection robot |

|
| 图 9 巡检机器人实验过程 Fig.9 Experimental process of inspection robot |
从图 7可以看出, 刚开始机器人不在设定的初始位置, 在设计控制器作用下, 经过一段时间逐渐靠近目标轨迹。从图 8可以看出, 航向角θ的偏差出现3次较大的波动, 是机器人在3次方向转换中角度误差过大导致的; 从角速度和线速度的曲线可以看出, 机器人的输出较为稳定, 由于存在未知扰动, 产生速度抖动的情况。
4 结论针对火灾预警巡检机器人的轨迹跟踪问题,首先建立了机器人的运动学模型,借助运动学模型建立误差模型,依据误差模型推导出误差方程;其次,考虑到经典控制器存在收敛速度慢、抖动较多等情况,在经典控制律基础上引入新的虚拟状态变量xe,建立反演控制技术的运动学控制律;最后用Lyapunov证明所设计控制律的稳定性。仿真和实物验证结果表明,火灾预警巡检机器人的反演控制器能够有效跟踪给定的目标轨迹,同时可以有效减少误差量和输出量在达到稳定状态之前的抖动次数,并减小控制器收敛时间。
| [1] |
孙忠廷, 柏建军, 陈炳旭, 等. 轮式移动机器人自适应轨迹跟踪控制[J/OL]. 控制工程, 2020: 1-6. [2021-04-12].
https://doi.org/10.14107/j.cnki.kzgc.20200387.
|
| [2] |
KANAYAMA Y, KIMURA Y, MIYAZAKI F, et al. A stable tracking control method for an autonomous mobile robot[C]. Proceedings of IEEE International Conference on Robotics and Automation. Cininnati USA: IEEE, 1990: 384-389.
|
| [3] |
曹锦波, 潘海鹏, 张益波. 基于改进型非线性干扰观测器的爬壁机器人轨迹跟踪[J]. 计算机系统应用, 2021, 30(2): 28-34. |
| [4] |
李卫兵, 吴琼. 基于反步法的轮式移动机器人轨迹跟踪控制算法[J]. 电子测量技术, 2018, 41(19): 54-58. |
| [5] |
ZHANG P, XUE H F, GAO S, et al. Distributed adaptive consensus tracking control for multi-agent system with communication constraints[J]. IEEE Transactions on Parallel and Distributed Systems, 2021, 32(6): 1293-1306. DOI:10.1109/TPDS.2020.3048383 |
| [6] |
YOUSUF B M, KHAN A S, KHAN S M. Dynamic modeling and tracking for nonholonomic mobile robot using PID and back-stepping[J]. Advanced Control for Applications: Engineering and Industrial Systems, 2021, 3(3): e71. |
| [7] |
宋立业, 邢飞. 移动机器人自适应神经滑模轨迹跟踪控制[J]. 控制工程, 2018, 25(11): 1965-1970. |
| [8] |
尤波, 张乐超, 李智, 等. 轮式移动机器人的模糊滑模轨迹跟踪控制[J]. 计算机仿真, 2019, 36(2): 307-313. DOI:10.3969/j.issn.1006-9348.2019.02.068 |
| [9] |
吴运雄, 曾碧. 基于深度强化学习的移动机器人轨迹跟踪和动态避障[J]. 广东工业大学学报, 2019, 36(1): 42-50. DOI:10.12052/gdutxb.180029 |
| [10] |
姜烽, 申燚, 张成, 等. 基于差分进化遗传优化的移动机器人轨迹跟踪控制[J]. 机械与电子, 2016, 34(7): 67-70. DOI:10.3969/j.issn.1001-2257.2016.07.017 |
| [11] |
沈智鹏, 张晓玲. 带扰动补偿的移动机器人轨迹跟踪反演控制[J]. 控制工程, 2019, 26(3): 398-404. |
| [12] |
崔明月, 孙棣华, 李永福, 等. 轮子纵向打滑条件下的移动机器人自适应跟踪控制[J]. 控制与决策, 2013, 28(5): 664-670. |
| [13] |
刘佳, 李春书. 基于Backstepping方法的轮式移动机器人轨迹跟踪研究[J]. 机电工程技术, 2011, 40(1): 79-82, 113. DOI:10.3969/j.issn.1009-9492.2011.01.023 |
| [14] |
徐俊艳, 张培仁. 非完整轮式移动机器人轨迹跟踪控制研究[J]. 中国科学技术大学学报, 2004, 34(3): 376-380. DOI:10.3969/j.issn.0253-2778.2004.03.017 |
| [15] |
马海涛. 非完整轮式移动机器人的运动控制[D]. 合肥: 中国科学技术大学, 2009.
|



