2. 广西壮族自治区海洋环境监测中心站, 广西北海 536000
2. Marine Environmental Monitoring Center of Guangxi Zhuang Autonomous Region, Beihai, Guangxi, 536000, China
传统的海洋环境监测工作方式主要是通过船只走航,依靠人工采集样品后在实验室进行分析,最后根据分析结果来判定海洋环境质量。近几十年来,随着遥感技术的快速发展,以及传感技术和无线数据传输技术的进步,现代海洋环境监测已经进入立体化的新时代。要实现海洋环境监测立体化,除不需要大量人力物力就可在海洋环境恶劣的情况下进行有效工作,并具有自动、长期、连续、实时收集海洋环境监测数据的自动监测浮标外,遥感是另一种重要的技术手段。遥感技术具有快速、连续、范围广、可视化程度高等特点,在大尺度环境状况和非点源污染监测方面具有明显优势[1]。Hakvoort等[2]使用机载成像光谱数据结合矩阵反演技术, 对Veluwe湖泊的有色可溶性有机物(CDOM)、叶绿素a等水质参数进行反演, 获得较好的效果。阎福礼等[3]使用MODIS数据对富营养化程度较高的太湖进行水质参数反演。郑炎辉等[4]利用GF-1 WFV遥感影像和BP神经网络模型,建立广东东风水库叶绿素a、透明度、总磷、总氮等水质参数反演模型。Pahlevan等[5]以美国路易斯安那州Grand Lake为研究区域,使用Sentinel-2和Landsat-8卫星数据产品进行遥感反射率的定量和定性验证,反演水质参数总悬浮物浓度。崔文君等[6]基于Landsat-8 OLI卫星遥感数据,发现Band 3和Band 4是反演珠江口近岸海域溶解氧的最佳波段组合,利用实测光谱一阶微分值构建模型得出的平均相对误差为19.2%。王冰等[7]使用Landsat TM影像结合实测数据获得呼伦湖溶解氧敏感波段,建立反演模型,约半数点位相对误差超过10%。总体来说,针对淡水湖泊叶绿素a、营养盐类等水质参数反演的卫星遥感研究较多,而对海水中溶解氧的遥感反演研究较少,且已有研究主要使用Landsat系列卫星影像数据,分辨率较低,且得到的模型精度一般。
溶解氧(Dissolved Oxygen,DO)指溶解在水中的分子态氧,溶解氧可能会因为藻类的生长而过饱和,当水体受有机或无机还原性物质污染时,溶解氧会降低[8]。广西钦州湾位于北部湾北部,由内湾(茅尾海)和外湾(钦州湾)构成,中间狭窄,两端宽阔,东、西、北三面为陆地所环绕,南面与北部湾相通,是一个半封闭型的天然海湾[9]。近十年来,钦州湾一直是北部湾近岸海域中污染最严重的海区之一,尤其是钦州湾内湾茅尾海海域,局部海域常年为第四类或劣四类海水水质[10]。同时,溶解氧作为赤潮发生前后重要的水质参数之一[11],对其展开研究在海洋生态方面具有重要意义。目前,虽然广西在近岸海域海洋自动监测上已有一定的基础,但是缺少以遥感技术为手段,对广西近岸海域水质进行大面积监测的研究工作。本文利用遥感手段,基于自动监测数据,建立钦州湾的溶解氧反演模型,为钦州湾海域的合理开发、科学管理提供技术支撑。
1 材料与方法 1.1 研究区域与数据获取研究区域位于广西北部湾北部钦州湾,即21°33′36″—21°55′12″E,108°24′36″—108°43′48″N[12]。溶解氧实测数据来自广西近岸海域水质自动监测网络布设在钦州湾的3个自动监测站位(Z1-Z3,见图 1)。监测仪器为YSI 6600V2多参数水质分析仪,可每0.5 h出具一次溶解氧监测结果,高频率的溶解氧实测数据可在较大程度内与Sentinel-2卫星影像的成像时间接近。

|
| 图 1 研究区域及自动监测站位示意图 Fig.1 Location of study area and automatic monitoring stations |
Sentinel-2系列卫星中的Sentinel-2 A于2015年6月23日发射,携带一枚多光谱成像仪,覆盖13个光谱波段,卫星传感器扫描宽度达290 km,光谱范围为0.4—2.4 μm。其在可见光、近红外到短波红外具有不同的空间分辨率,分别为10 m (4个波段),20 m (6个波段)和60 m (3个波段),其中可见光波段及近红外波段空间分辨率为10 m,可用于观测地球土地覆盖变化,森林、湖水及近海水域污染情况[12]。本文选取2017—2019年研究区域内云量 < 30%的影像作为影像数据源。
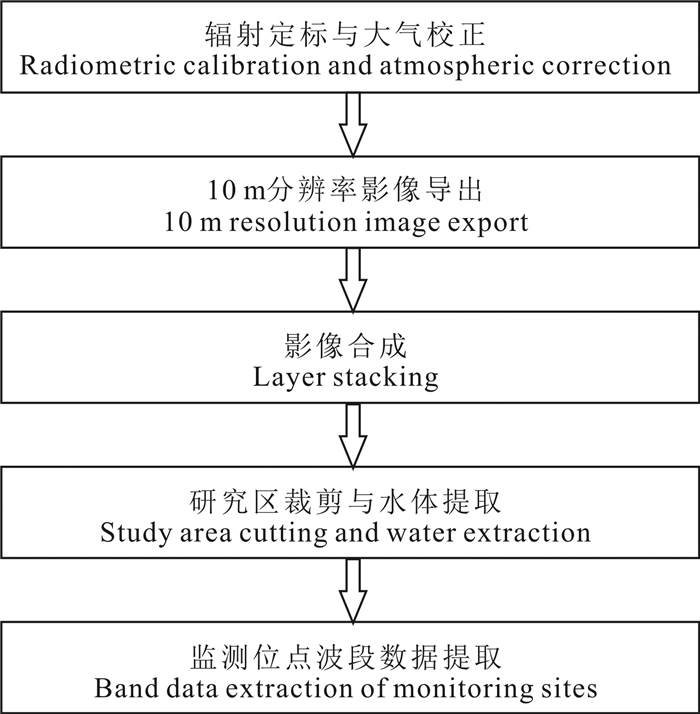
1.2 影像数据预处理采用SNAP软件中附带的插件Sen2cor v2.8.0对影像进行辐射定标和大气校正。校正完成之后,对影像进行重采样,将蓝、绿、红、近红外(宽)4幅10 m分辨率的单波段影像导出为ENVI格式,并以Layer Stacking工具重新合成为一幅影像。为方便影像数据的进一步处理和专注于研究区的影像数据分析,对研究区域进行裁剪并提取监测点位的波段数据。影像预处理流程图如图 2所示。
|
| 图 2 Sentinel-2影像预处理流程 Fig.2 Sentinel-2 image preprocessing flow |
1.3 构建波段组合
本文以溶解氧浓度(DO)作为溶解氧反演模型的因变量,以波段组合作为自变量,通过建立数学模型设法找出最能代表溶解氧浓度与波段组合之间关系的数学表达式。Sentinel-2搭载的传感器上有4种分辨率为10 m的波段,为表述方便,本文以B1—B4来分别表示Sentinel-2传感器的蓝、绿、红、近红外波段(表 1)。将自动监测站位所在像元的4个波段反射率值导出,通过相加、相比、取倒数、取对数等方式进行波段组合的构建。
| 编号 No. |
波段 Band |
中心波长 Central wavelength (nm) |
分辨率 Resolution (m) |
带宽 Bandwidth (nm) |
| B1 | 蓝光 Blue light |
490 | 10 | 65 |
| B2 | 绿光 Green light |
560 | 10 | 35 |
| B3 | 红光 Red light |
665 | 10 | 30 |
| B4 | 近红外光(宽) Near infrared light (wide) |
842 | 10 | 115 |
1.4 Pearson相关性分析
Pearson相关系数(R)是一种线性相关系数,反映2个变量间的线性相关程度[13],可用来分析不同波段组合与自动监测站位溶解氧实测值的相关程度,从中筛选出敏感程度最高的波段组合。其公式如下:
| $ R=\frac{\sum\nolimits_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum\nolimits_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2} \sum\nolimits_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}}, $ |
式中,R表示自变量x和因变量y的相关系数,n为样本量,xi、yi分别为x和y的第i个样本值,x、y分别为x和y的平均值。R>0,说明2个变量具有正相关关系;R < 0,说明2个变量呈负相关关系。通常来说,波段组合与溶解氧浓度的|R|越高,用该波段组合来构建的反演模型的模型精度越高。
1.5 回归分析回归分析是指确定自变量与因变量间相互依赖的定量关系的统计分析过程。虽然自变量x和因变量y之间可能没有严格、确定的函数关系,但可以通过回归分析建立起变量之间的相关关系近似数学表达式[14]。
(1) 一元线性回归:采用相关性最高的波段组合依次作为自变量x来进行一元线性回归。
(2) 一元非线性回归:采用相关性最高的波段组合的对数值依次作为自变量x来进行回归建模,筛选出模型精度最高的模型。
(3) 二元线性回归:以相关性最高的两组波段组合共同作为自变量x。
(4) 三元非线性回归:以相关性最高的三组波段组合共同作为自变量x。
4种回归模型均以溶解氧浓度实测值作为因变量y,最后筛选出显著性较强、验证精度最高的回归模型。
1.6 逐步回归分析逐步回归分析是一个删除不显著因素、保留显著因素的过程。逐步回归分析在引入和剔除变量的过程中可以保证最后保留的变量是互相独立、无多重共线性的,非常适用于多个自变量的多元回归模型构建[15]。基于Sentinel-2影像数据构建的波段组合和溶解氧实测数据进行逐步回归分析,剔除不显著波段组合,最终得到的逐步回归模型。
1.7 模型精度验证反演模型的验证非常重要,要判断模型是否稳定可靠,必须从多个角度来对反演模型的精度进行验证。本研究采用决定系数(R2)、平均相对误差(MRE)、均方根误差(RMSE)进行精度验证。
(1) R2:将实测值与模型输出值进行线性拟合,线性拟合的R2值越大,表明模型输出值与实测值之间的相关性越高。值得注意的是,相关性高并不意味着模型输出值与实测值相近,因此不能仅凭R2值来判断模型精度。
(2) MRE:表明模型输出值与实测值的偏离程度。计算公式如下:
| $ \begin{array}{c} \rm{MRE}(\%)= \\ \frac{1}{\text { 样本数量 }} \sum \frac{\mid \text { 实测值一模型输出值 } \mid}{\text { 实测值 }} \times 100 \% \text { 。} \end{array} $ |
(3) RMSE:亦称标准误差,均方根误差对一组测量中的特大或特小误差非常敏感,所以能够很好地反映测量的精密度。计算公式如下:
| $ \mathrm{RMSE}=\sqrt{\frac{\sum(\text { 实测值一模型输出值 })^{2}}{\text { 样本数量 }}} \text { 。} $ |
本文共获得370种波段组合,以下选取了Pearson相关性(R)较高的24个波段组合(表 2),研究区域中有3个组合波段与溶解氧浓度相关性效果较好,分别是1/B3、lnB3/(lnB1+lnB2)和B3/(B1+B2),其Pearson相关系数(R)分别为0.905 2,-0.897 0和-0.889 2,已基本满足钦州湾溶解氧浓度反演的需求。
| 序号 No. |
正相关 Positive correlation |
序号 No. |
负相关 Negative correlation |
|||
| 波段组合 Band combinations |
R | 波段组合 Band combinations |
R | |||
| 1 | 1/B3 | 0.905 2 | 13 | lnB3/(lnB1+lnB2) | -0.897 0 | |
| 2 | lnB1/(lnB1+lnB3) | 0.882 3 | 14 | B3/(B1+B2) | -0.889 2 | |
| 3 | lnB2/(lnB2+lnB3) | 0.881 0 | 15 | ln[B3/(B1+B2)] | -0.888 2 | |
| 4 | lnB1/lnB3 | 0.880 9 | 16 | B3/B2-B1/B3 | -0.886 0 | |
| 5 | lnB2/lnB3 | 0.880 4 | 17 | lnB3/lnB1 | -0.883 4 | |
| 6 | (1/B3-1/B2)×B1 | 0.876 3 | 18 | lnB3/(lnB1+lnB3) | -0.882 3 | |
| 7 | ln[B1/(B1+B3)] | 0.874 8 | 19 | lnB3/lnB2 | -0.881 0 | |
| 8 | B1/(B1+B3) | 0.873 6 | 20 | lnB3/(lnB2+lnB3) | -0.881 0 | |
| 9 | ln(B1/B3) | 0.873 0 | 21 | B3×B3/(B1×B2) | -0.880 5 | |
| 10 | lnB1-lnB3 | 0.873 0 | 22 | B3/B1-B2/B3 | -0.879 0 | |
| 11 | B2/B1+B1/B3 | 0.871 3 | 23 | B1/B2-B1/B3 | -0.876 3 | |
| 12 | B1/B2+B2/B3 | 0.869 3 | 24 | (1/B2-1/B3)×B1 | -0.876 3 | |
2.2 建模结果
在相关性分析结果的基础之上,通过筛选得到48个影像质量良好的点位监测数据,随机抽取其中的40个点位分别进行回归建模尝试,并获得4个回归反演模型公式:
(1) 一元线性回归模型y=1100.345x+4.925,x=1/B3,R2=0.837 8;
(2) 一元非线性回归方程模型y=1.5995x+17.209,x=ln(B1/B3),R2=0.752 9;
(3) 二元线性回归模型y=603.192x1-29.39x2+19.745,x1=1/B3,x2=lnB3/(lnB1+lnB2),R2=0.857 3;
(4) 三元非线性回归模型y=605.842x1-27.8376x2-0.3227x3+19.12,x1=1/B3,x2=lnB3/(lnB1+lnB2),x3=B3/(B1+B2),R2=0.857 3;
以及逐步回归分析模型:y=771.854x1-1.476x2+6.435,x1=1/B3,x2=B3×B3/(B1×B1),R2=0.863。
随机抽取剩余的8个点位对以上5个模型公式进行精度验证,结果如表 3所示。通过对5种回归模型的综合比较可知(表 3),逐步回归模型的决定系数、平均相对误差和均方根误差是5种模型中最小的。平均相对误差和均方根误差越小,说明模型输出结果与实际值更贴近,反演模型的稳定性也更有保证。
| 序号 No. |
模型公式 Model |
决定系数 R2 |
平均相对误差 MRE (%) |
均方根误差 RMSE |
| 1 | y=1100.345x+4.925 | 0.626 7 | 7.56 | 0.584 5 |
| 2 | y=1.5995x+17.209 | 0.600 1 | 8.39 | 0.611 7 |
| 3 | y=603.192x1-29.39x2+19.745 | 0.639 5 | 8.21 | 0.617 5 |
| 4 | y=605.842x1-27.8376x2-0.3227x3+19.12 | 0.639 5 | 8.21 | 0.616 5 |
| 5 | y=771.854x1-1.476x2+6.435 | 0.654 3 | 6.47 | 0.521 1 |
综上考虑,选择逐步回归模型y=771.854x1-1.476x2+6.435(模型精度R2=0.863)作为钦州湾溶解氧的反演模型,对应的波段组合为1/B3和B3×B3/(B1×B1)。
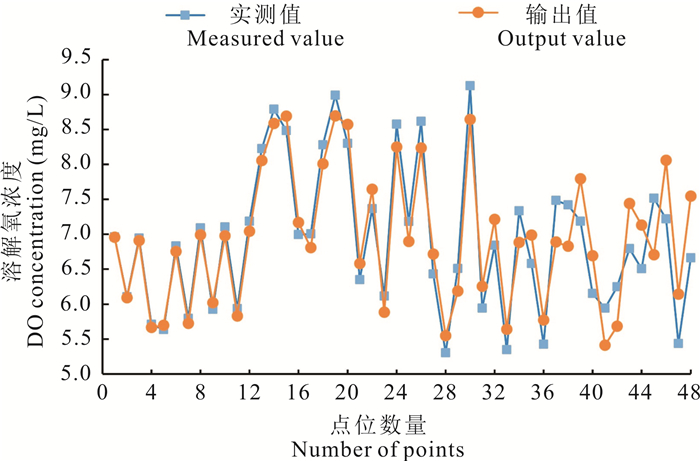
另外,为避免随机抽取点位进行验证可能带来的验证结果的偶然性,进一步对逐步回归模型所有点位的输出值与实测值进行比较分析。由图 3可知,实测值曲线与模型输出值曲线保持了较高的吻合度,在前30个点位(约占总点位数的2/3)中,模型输出值与实测值之间的相对误差均低于5%,表明模型的稳定性较强,展现了较高的模型精度。
|
| 图 3 逐步回归模型输出值与实测值比较分析 Fig.3 Comparison and analysis of output value and measured value of stepwise regression model |
2.3 钦州湾溶解氧时空分布特征
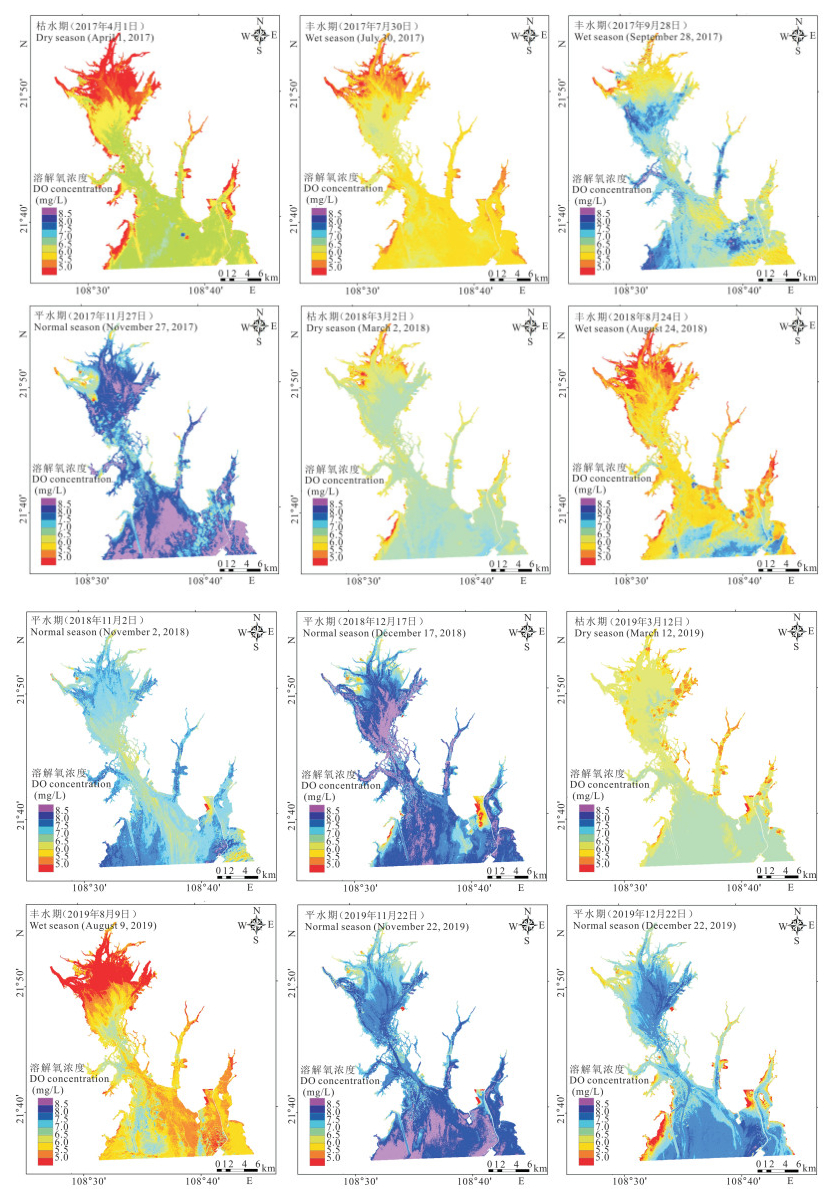
通过前面建立的溶解氧反演模型计算,得到基于Sentinel-2 A卫星2017—2019年遥感数据的钦州湾溶解氧浓度时空分布结果(图 4)。从反演结果上看,2017—2019年钦州湾溶解氧浓度存在明显的时间变化,按照枯水期(3,4月)、丰水期(7—9月)、平水期(11,12月)划分,研究区域每年都基本呈现溶解氧浓度丰水期<枯水期<平水期的规律。按四季划分,钦州湾溶解氧浓度基本呈现夏季最低、春季适中、秋冬最高的特点。在空间分布上,2017—2019年钦州湾溶解氧浓度均呈现内湾<外湾的特点,且内湾溶解氧浓度分布不均匀,越靠近河口的位置溶解氧浓度越低。
|
| 图 4 2017—2019年钦州湾溶解氧浓度反演结果 Fig.4 The dissolved oxygen concentration inversion result of Qinzhou Bay during 2017—2019 |
3 结论
本研究基于Sentinel-2系列卫星遥感影像并结合自动监测实测溶解氧浓度数据,建立广西钦州湾溶解氧反演模型,得出1/B3、lnB3/(lnB1+lnB2)和B3/(B1+B2) 3个波段组合与溶解氧浓度相关性效果较好。采用最佳敏感波段和回归模型构建钦州湾的溶解氧浓度反演模型,逐步回归模型稳定性较佳,模型精度R2达到0.863。通过反演结果得出2017—2019年部分时段钦州湾溶解氧浓度分布图, 直观显示钦州湾溶解氧的空间分布状况,可为钦州湾溶解氧实时遥感监测提供理论依据与技术支撑。
以往水质反演所使用的实测数据大多为卫星过境当天,通过人工采集样品的方式得到水质监测数据,而本研究使用的0.5 h/次的高频率自动监测数据能在较大限度内与遥感影像数据接近,在很大程度上提高了模型精度。因此可以预见,自动监测与遥感技术相结合的方式,在未来会有较好的发展潜力。采用最佳敏感波段和回归模型方式构建钦州湾的溶解氧浓度反演模型,优势在于模型简单、易于实现,且最终得到了较好的反演效果。
本文实现了基于遥感技术对钦州湾溶解氧浓度的大范围动态监测,得出的模型精度较佳,是一次较好的尝试。不过,影响钦州湾水环境的重要指标有很多,在未来的研究中仍需对其他指标进行研究,例如石油类、营养盐等,使反演模型更加全面和实用。
| [1] |
陈令新, 王巧宁, 孙西艳. 海洋环境分析监测技术[M]. 北京: 科学出版社, 2018.
|
| [2] |
HAKVOORT H, DE-HAAN J, JORDANS R, et al. Towards airborne remote sensing of water quality in the Netherlans-validation and error analysis[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2002, 57(3): 171-183. DOI:10.1016/S0924-2716(02)00120-X |
| [3] |
阎福礼, 林亚森, 王世新, 等. 太湖富营养化水体比辐射率测量及MODIS水体温度反演应用[J]. 中国科学院大学学报, 2019, 36(6): 784-793. |
| [4] |
郑炎辉, 张园波, 何艳虎. 基于GF-1 WFV影像与神经网络模型的水库水质多参数反演研究[J]. 人民珠江, 2020, 41(7): 57-62, 84. |
| [5] |
PAHLEVAN N, SARKAR S, FRANZ B A, et al. Sentinel-2 Multi Spectral Instrument (MSI) data processing for aquatic science applications:Demonstrations and validations[J]. Remote Sensing of Environment, 2017, 201: 47-56. DOI:10.1016/j.rse.2017.08.033 |
| [6] |
崔文君, 夏丽华, 解学通, 等. 基于实测光谱的珠江口溶解氧反演模型[J]. 广州大学学报:自然科学版, 2017, 16(6): 84-92. DOI:10.3969/j.issn.1671-4229.2017.06.013 |
| [7] |
王冰, 安慧君, 吕昌伟. 基于多源遥感数据的呼伦湖溶解氧反演模型[J]. 生态学杂志, 2013, 32(4): 993-998. |
| [8] |
国家环境保护总局《水和废水监测分析方法》编委会. 水和废水监测分析方法[M]. 4版. 北京: 中国环境科学出版社, 2002.
|
| [9] |
张荣灿, 姜发军, 陈宪云, 等. 钦州湾近岸海域水质污染状况评价[J]. 广西科学, 2014, 21(4): 403-410. DOI:10.3969/j.issn.1005-9164.2014.04.014 |
| [10] |
蓝文陆, 李天深, 罗金福. 广西钦州湾环境与生态研究[M]. 北京: 科学出版社, 2020.
|
| [11] |
韦蔓新, 何本茂, 赖廷和. 廉州湾赤潮形成期间pH值和溶解氧的时空分布及其与环境因素的关系[J]. 广西科学, 2004, 11(3): 221-224. DOI:10.3969/j.issn.1005-9164.2004.03.017 |
| [12] |
中国海湾志编纂委员会. 中国海湾志第十二分册广西海湾[M]. 北京: 海洋出版社, 1993.
|
| [13] |
龚燃. 哨兵-2A光学成像卫星发射升空[J]. 国际太空, 2015(8): 36-40. |
| [14] |
郭立焕. 回归分析方法的原理及应用[J]. 山西财经学院学报, 1982(4): 54-60. |
| [15] |
胡松伟. 变深度发射性能可靠性影响因素多元逐步回归分析[J]. 兵工学报, 2017, 38(5): 986-994. DOI:10.3969/j.issn.1000-1093.2017.05.019 |



