根据工程应用发展的需求,一系列群智能算法应运而生,如粒子群算法[1](Particle swarm optimization, PSO)通过模拟鸟群的觅食过程迭代寻优;蝙蝠算法[2] (Bat algorithm, BA)是通过模仿蝙蝠声呐探测飞行的方式迭代寻优;萤火虫算法[3](Firefly algorithm, FA)通过模拟萤火虫在晚上的群聚活动进行寻优。萤火虫算法被广泛地运用于选址问题、预测模型、背包问题等工程应用问题。萤火虫算法作为一种新的群体智能仿生优化算法,发展时间尚短,算法本身存在着对于初始解分布的依赖性、后期收敛速度慢、易于停滞、早熟和求解精度低等缺陷[4]。近些年,相关学者对萤火虫算法进行了多角度的改进。Łuckasik等[5]于2009年对FA改进,并对算法的参数进行研究,改进后的FA提高了求解精度,但求解速度较慢。冯艳红等[6]提出了基于混沌理论的动态种群萤火虫优化算法(CDPFA),该算法运用立方映射混沌初始化萤火虫初始位置,取得了较好的效果,进一步提高了算法的寻优精度和求解速度。王吉权等[7]结合了遗传算法,提出一种基于目标函数自适应惯性权重的萤火虫算法。测试函数表明,通过此策略的改进,萤火虫算法个体之间的收敛速度可以得到有效地提高。Gandomi等[8]更是将混沌映射的理论应用到了萤火虫算法中,利用混沌理论对萤火虫的吸引度β和光吸收参数γ进行了改进,并用12种不同的混沌映射进行了仿真验证。与标准萤火虫算法比较,经过改进的萤火虫算法具有更高的鲁棒性和实用性。付强等[9]根据改进的自调节步长的萤火虫搜索策略改善PSO的局部搜索能力,避免PSO陷入局部最小值。郝晓莹等[10]提出一种通过粒子群优化的粒子搜索, 对不同优化问题自适应选取萤火虫算法参数值的优质组合的方法。萤火虫算法虽然有诸多的改进方法,但是总存在着些许不足,所以我们在萤火虫算法的基础上,引进了蝙蝠种群来协助萤火虫种群进行寻优,利用了蝙蝠算法具有较强的局部搜索能力这个特点,对全局最优个体附近进行详细的局部搜索;并加强蝙蝠种群和萤火虫种群在寻优过程中的信息交互,协同寻优;最后对全局最优进行高斯扰动以增加种群的多样性。该算法解决了萤火虫算法本身存在着对于初始解分布的依赖性、后期收敛速度慢、易于停滞、早熟和求解精度低等缺陷,可广泛地运用在解决工程应用问题或者人工智能领域,有效地提高工作效率与精度,为这些领域的研究应用建立基础。
1 材料与方法 1.1 蝙蝠算法蝙蝠算法是根据蝙蝠在捕食的过程中利用回声来定位猎物的自然现象而提出的一种群智能算法[11]。蝙蝠利用回声的差异来判断猎物之间的差异,再根据猎物的接近程度自动调整他们发出脉冲的频率,通过不断的迭代从而寻找到猎物的位置。
蝙蝠以速度v随机飞行,并用不同的频率Q和音量A搜索猎物。标准蝙蝠算法通过公式(1)~(3)对蝙蝠个体的速度以及位置进行更新。
| $ {Q_i} = {Q_{\min }} + \left( {{Q_{\max }} - {Q_{\min }}} \right)\beta , $ | (1) |
| $ v_i^t = v_i^t + \left( {X_i^{t - 1} - {X_{{\rm{Gbest}}}}} \right){Q_i}, $ | (2) |
| $ X_i^t = X_i^{t - 1} + v_i^t, $ | (3) |
其中,Qi是第i个蝙蝠飞行的频率,Qmax和Qmin分别是频率取值范围的上限和下限;β是[0, 1]上服从均匀分布的随机向量;vit和vit-1分别是第i个蝙蝠在t时刻和t-1时刻的速度。XGbest是通过所有蝙蝠搜索到的解中结果最好的蝙蝠个体所在的位置; Xit和Xit-1分别是第i个蝙蝠在t时刻和t-1时刻所在的位置。
对于局部搜索部分,选择最优解蝙蝠按照随机游走法则生成一只新的蝙蝠从而得到局部新解:
| $ {X_{{\rm{new}}}} = {X_{{\rm{Gbest}}}} + \varepsilon \times {A^t}, $ | (4) |
其中ε是[-1, 1]的一个随机变量,At是t时刻中所有蝙蝠的平均响度。
此外,响度Ai和脉冲发射率ri也随着迭代的进行而相应地更新。响度和脉冲的更新公式分别为
| $ A_i^t = a \times A_i^{t - 1}, $ | (5) |
| $ r_i^t = r_i^0 \times [1 - \exp ( - yt)], $ | (6) |
其中α和y取常数,对于任何0<a<1和0<y,当t→∞有
| $ A_i^t \to 0, r_i^t \to r_i^0, $ | (7) |
Ait是蝙蝠i在t时刻发出的响度,ri0和rit分别是蝙蝠i在初始时刻和t时刻发出的脉冲。
1.2 萤火虫算法萤火虫算法是Yang[3]在2008年提出的,他把空间各点看成萤火虫,利用发光强的萤火虫会吸引发光弱的萤火虫的特点来进行寻优。在发光弱的萤火虫向发光强的萤火虫移动的过程中,完成位置的迭代,从而找出最优位置,即完成寻优过程[12]。
萤火虫的相对亮度:
| $ I = {I_0}{e^{ - y{r_{ij}}}}, $ | (8) |
其中,I0表示最亮萤火虫的亮度,即自身(r=0处)荧光亮度,与目标函数值相关,即目标函数值越好,自身亮度越高;y表示光吸收系数,因为荧光会随着距离的增加和传播媒介的吸收逐渐减弱,所以设置光强吸收系数以体现此特性,可设置为常数;rij表示萤火虫i与j之间的距离。
萤火虫的相互吸引度β:
| $ \beta (r) = {\beta _0}{e^{ - yr_{ij}^2}}, $ | (9) |
其中,β0表示最大吸引度,即光源处(r=r0=0处)的吸引度。
位移更新公式:
| $ X_i^t = X_i^{t - 1} + \beta \left[ {X_j^{t - 1} - X_i^{t - 1} + a\left( {rand - \frac{1}{2}} \right)} \right], $ | (10) |
其中Xit与Xjt表示i, j两个萤火虫在t时刻的位置,α为步长因子,rand为[0, 1]上服从均匀分布的随机数。
1.3 混合算法根据萤火虫的位置更新公式(10)可知,当两只萤火虫距离靠近时将会进一步加速收敛导致陷入早熟,大量萤火虫聚集在局部最优从而错过全局最优解。本文对萤火虫算法的局部搜索进行改进,将蝙蝠算法中最优解随机游走的思想融入到萤火虫位置更新过程中,同时对该游走进行高斯扰动,增加种群的多样性,使得种群的局部搜索能力更强,并避免过快地陷入局部最优。我们将两种算法融合在一起的算法称为蝙蝠萤火虫混合算法(Hybrid bat and firefly algorithm, HBAFA)。
首先初始化蝙蝠种群Xi,在全局最优的个体XGbest附近进行局部寻优,产生的新个体BatX,即当第i个蝙蝠Xi发出的脉冲ri小于产生的随机生成的脉冲,则对全局最优个体XGbest进行高斯扰动产生一个新的个体并存放在BatX中。如果BatX的适应度值优于Xi且其响度Ai大于随机生成的响度,则用BatX替换Xi。其高斯扰动的公式如下:
| $ \begin{array}{l} \mathit{Bat}X = {X_{{\rm{ Gbest }}}} \times (N(0, 1) + 1)\quad {\rm{ as }}\quad {r_i} < \\ \mathit{rand}, \end{array} $ | (11) |
其中XGbest是全局最优个体,N(0, 1)是服从均值为0,方差是1的高斯分布函数,ri是第i个蝙蝠个体发出的脉冲,rand是在[0, 1]上服从均匀分布的随机数。
| $ \begin{array}{l} {X_i} = \mathit{Bat}X{\rm{ as }}\;f(\mathit{Bat}X) < f\left( {{X_i}} \right){\rm{ \& \& }}{A_i} > \\ \mathit{rand,} \end{array} $ | (12) |
其中Xi是个体i的位置,Ai是个体i发出的响度,rand是在[0, 1]上服从均匀分布的随机数。
蝙蝠通过在XGbest周围发射脉冲信号产生局部解BatX来实现局部最优搜索,并通过该蝙蝠个体发出的响度和其位置的优劣来更新种群,同时通过萤火虫算法进行全局最优搜索,与萤火虫算法实现了信息上的交互,增加了萤火虫的种群多样性,加强了算法的局部搜索能力,弥补了萤火虫算法在局部搜索上的不足,使萤火虫算法得到了优化。
1.4 HBAFA算法流程通过上述HBAFA思想分析,下面给出HBAFA算法的详细优化步骤。
HBAFA算法步骤如下:
Step 1 初始化相关参数,随机生成蝙蝠种群,并根据公式(11)生成BatX;
Step 2 若迭代次数未到达设定次数,转Step 3,否则结束算法;
Step 3 判断个体的脉冲ri是否小于随机数rand,小于则生成BatX,否则转Step 4;
Step 4 若f(BatX)<f(Xi) & & Ai>rand,则使用公式(12)将萤火虫个体替换成蝙蝠个体,并且使用公式(5)和(6)分别更新响度Ai和脉冲ri,否则转Step 5;
Step 5 计算任意两只萤火虫之间的欧式距离和相互吸引度β,然后使用公式(10)更新萤火虫个体的位置;
Step 6 判断是否达到终止条件(一般为达到最大迭代次数或者达到设定精度),若达到终止条件, 则迭代终止,否则转向Step 2。
2 结果与分析 2.1 测试函数选择6个常用的测试函数来检验混合算法的有效性,测试函数如表 1所示。
| Fun Name | Fun | Range | Best |
| Sphere | [-100, 100] | 0 | |
| Rosenbrock | [-10, 10] | 0 | |
| Griewank | [-600, 600] | 0 | |
| Rastrigin | [-5.12, 5.12] | 0 | |
| Ackley | [-32, 32] | 0 | |
| Schaffer′s F6 | [-100, 100] | 0 |
2.2 实验环境和参数设置
算法测试操作系统为Windows 7,CPU为Inter E5-1620v3,主频3.5 Ghz,内存16 GB,Matlab2016a。设置种群大小Popsize均为40,寻优精度设置为10∧(-5),最大迭代次数设置为1 000次。HBAFA初始音量A0=1,最小音量Amin=0;最大脉冲值rmax=1,最小脉冲值rmin=0;萤火虫的步长因子α=0.2;光吸收系数y=1。BA初始音量也设置为A0=1,最小音量Amin=0,最大脉冲值rmax=1,最小脉冲值rmin=0,α和y取0.9。SPSO粒子移动速度上下限设置为搜索空间的10%。萤火虫算法步长因子α=0.2,光吸收系数y=1。
2.3 收敛性分析为降低偶然因素对实验结果的影响,我们对表 1的测试函数进行30次独立重复实验,并记录每种算法在每次迭代结束后所得到的实验数据,在30次实验中所得到的最差值Worst、最优值Best、平均值Avg以及标准偏差Std如表 2所示。
| Fun | Dim | Alg | Best | Worst | Avg | Std |
| f1 | 30 | HBAFA | 0 | 0 | 0 | 0 |
| BA | 3.716E+3 | 1.668E+4 | 1.054E+4 | 3.182E+3 | ||
| FA | 5.126E+4 | 7.700E+4 | 6.539 E+4 | 6.295E+3 | ||
| SPSO | 3.442E+0 | 4.343E+1 | 2.160E+1 | 1.015E+1 | ||
| f2 | 30 | HBAFA | 3.232E-5 | 2.871E+1 | 2.488E+1 | 9.923E+0 |
| BA | 2.614E+7 | 1.332E+9 | 5.877E+8 | 2.877E+8 | ||
| FA | 1.408E+10 | 3.814E+10 | 2.909E+10 | 5.692E+9 | ||
| SPSO | 6.566E+3 | 6.744E+5 | 4.705E+4 | 1.200E+5 | ||
| f3 | 30 | HBAFA | 0 | 0 | 0 | 0 |
| BA | 1.869E+0 | 4.736E+0 | 3.611E+0 | 0.683E+0 | ||
| FA | 1.455E+1 | 2.099E+1 | 1.763E+1 | 1.681E+0 | ||
| SPSO | 0.353E+0 | 0.840E+0 | 0.587E+0 | 0.129E+0 | ||
| f4 | 30 | HBAFA | 0 | 0 | 0 | 0 |
| BA | 1.417E+4 | 2.239E+4 | 1.936E+4 | 2.047E+3 | ||
| FA | 4.900E+4 | 7.670E+4 | 6.402E+4 | 6.274E+3 | ||
| SPSO | 1.844E+2 | 4.662E+2 | 3.321E+2 | 6.983E+1 | ||
| f5 | 30 | HBAFA | 8.882E-16 | 8.882E-16 | 8.882E-16 | 0 |
| BA | 2.000E+1 | 2.000E+1 | 2.000E+1 | 3.906E-4 | ||
| FA | 2.150E+1 | 2.150E+1 | 2.136E+1 | 0.077E+0 | ||
| SPSO | 6.022E+0 | 2.047E+1 | 1.883E+1 | 4.147E+0 | ||
| f6 | 2 | HBAFA | 0 | 0 | 0 | 0 |
| BA | 0.010E+0 | 0.466E+0 | 0.234E+0 | 0.140E+0 | ||
| FA | 0.010E+0 | 0.415E+0 | 0.172E+0 | 0.120E+0 | ||
| SPSO | 0 | 0.010E+0 | 0.003E+0 | 0.004E+0 |
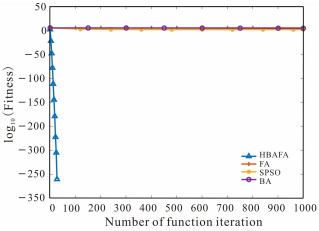
f1函数是二次函数型,在球面上具有单峰特性,也就是最值唯一极值。由图 1可知,在优化f1函数的过程中,HBAFA的收敛曲线十分陡峭,说明其收敛速度极快,较短的迭代次数就能达到非常高的寻优精度;而FA、SPSO和BA的收敛曲线较平缓,说明这3种算法的种群多样性较差,极易陷入局部最优解,收敛速度明显慢于HBAFA算法。在寻优过程中,HBAFA不到100次迭代,就能寻找到该函数的最优解0(由于寻优曲线图的纵坐标是log10(Fitness),当寻找到最优解时寻优曲线在图上无法显示);而其他3种算法的寻优能力较差,在迭代终止时也没能寻找到最优解。由表 2中f1的实验数据可知,在迭代结束(Iteration=1 000)时,HBAFA寻找到的平均解优于其他3种算法,且方差为0,说明该算法表现十分稳定,每次都能够在迭代结束前寻找到Sphere函数的最优解。综上所述,在Sphere函数的寻优过程中,HBAFA的收敛速度、收敛精度和稳定性都优于其他3种算法。
|
| 图 1 f1函数对比曲线 Fig.1 Contrast curve of function f1 |
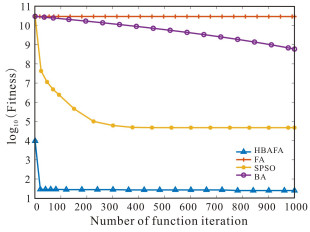
f2与其他5个函数图像不同,该函数在定义域内具有连续性,只有一个峰值,对应全局最小却在局部最优之间的波谷下,检测过程中极易检测到局部最优,但很难找到全局最佳点,是算法开发与尝试方面极其经典的检测函数。由图 2可知,在优化f2函数的前期,在迭代次数相同时,HBAFA的收敛速度和收敛精度均优于其他3种算法;在寻优后期,4种算法均陷入局部最优解;在迭代结束之后,4种算法均没有找到最优解。由表 2中f2的实验数据可知,在迭代结束之后,HBAFA寻找到的平均解Avg优于其他3种算法,因此HBAFA的收敛精度均优于其他3种算法。综上所述,HBAFA整体的收敛性能均优于其他3种算法。
|
| 图 2 f2函数对比曲线 Fig.2 Contrast curve of function f2 |
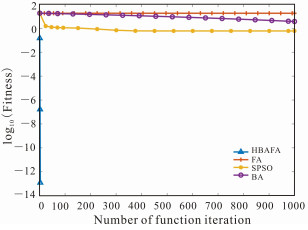
f3是高次函数型,其图像为非线性变化,都具有多个极值和多个图像峰,这些极值服从某种函数分布,可检验算法在多模以及高维的收敛情况。由图 3可知,在优化f3函数的前期,在迭代次数相同时,HBAFA的收敛速度和收敛精度均优于其他3种算法;在寻优后期,BA、SPSO和FA这3种算法均陷入局部最优解;在迭代结束之后,只有HBAFA找到最优解,并且在迭代次数不到100次就能寻找到最优解。由表 2中f3的实验数据可知,在迭代结束之后,HBAFA寻找到的平均解Avg优于其他3种算法,并且寻找到最优解,因此HBAFA的收敛精度均优于其他3种算法。综上所述,HBAFA整体的收敛性能均优于其他3种算法。
|
| 图 3 f3函数对比曲线 Fig.3 Contrast curve of function f3 |
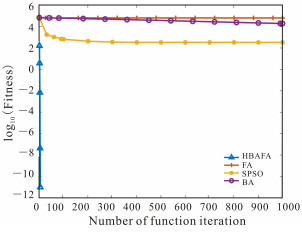
f4从函数分析、最值求解及其图像中不难看出,该函数存在大概10n个局部极小值,其中n表示空间的维数。由图 4可知,在优化f4函数的前期,在迭代次数相同时,HBAFA的收敛速度和收敛精度均优于其他3种算法;在寻优后期,BA、SPSO和FA这3种算法均陷入局部最优解;在迭代结束之后,只有HBAFA找到最优解,并且在迭代次数不到100次就能寻找到最优解。由表 2中f4的实验数据可知,在迭代结束之后,HBAFA寻找到的平均解Avg优于其他3种算法,并且寻找到最优解,因此HBAFA的收敛精度均优于其他3种算法。综上所述,HBAFA整体的收敛性能均优于其他3种算法。
|
| 图 4 f4函数对比曲线 Fig.4 Contrast curve of function f4 |
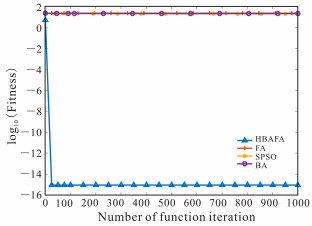
f5的函数图像复杂多变,所对应的搜索要求特别不易控制,检测过程中容易出现局部极值问题。由图 5能够看出,在优化Ackley函数的过程中,HBAFA在初期十分陡峭,说明在搜索初期收敛速度极快,较短的迭代次数就能达到非常高的寻优精度;而FA、SPSO和BA的收敛曲线较平缓,说明这3种算法的种群多样性较差,极易陷入局部最优解,收敛速度明显慢于HBAFA算法,且收敛精度低,远不能达到设定的收敛精度要求。由表 2中f5的实验数据可知,在迭代结束时,HBAFA寻找到的平均解优于其他3种算法,说明该算法表现十分稳定,每次都能够在迭代结束前寻找到Ackley函数较高精度的解。综上所述,在Ackley函数的寻优过程中,HBAFA的收敛性能都优于其他3种算法。
|
| 图 5 f5函数对比曲线 Fig.5 Contrast curve of function f5 |
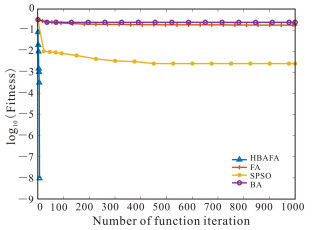
f6在检测过程中极不稳定,振荡现象非常明显,幅值很大。由图 6能够看出,在优化Schaffer's F6函数的过程中,HBAFA的收敛曲线在初期非常陡峭,说明在搜索初期收敛速度极快,不到100次迭代就能够搜索到Schaffer's F6函数的最优解0;而FA和BA的收敛曲线则十分平缓,两者收敛速度相当,收敛精度差别也不大,SPSO则有较陡峭的收敛曲线,且收敛精度略优于FA和BA,但都无法达到搜索精度的要求。由表 2中f6的实验数据可知,在迭代结束(Iteration=1 000)前,HBAFA寻找到的平均解优于其他3种算法,说明该算法表现十分稳定,每次都能够在迭代结束前寻找到Schaffer's F6函数的最优解。综上所述,在Schaffer's F6函数的寻优过程中,HBAFA的收敛性能都优于其他3种算法。
|
| 图 6 f6函数对比曲线 Fig.6 Contrast curve of function f6 |
HBAFA,FA,SPSO,BA相对应的检测显示输出曲线如图 1~6所示,FA和BA的表现相差不大,SPSO在函数f2,f3,f4,f6的性能比这两者优越,但效果也并不是十分理想。而HBAFA无论是在单峰函数Sphere、Rosenbrock还是多峰函数Griewank、Rastrigin、Ackley以及Schaffer,都能在迭代初期就有很好的表现,输出的适应度值好,收敛速度快,尤其是f1,f3,f4,f6在很早期就能够达到收敛。f3,f4,f5具有多个局部极值,可检验算法在多模以及高维的收敛情况,FA、SPSO、BA对这3个函数均无法寻找到最佳解,而HBAFA对于f3、f4能够寻到最优解,而对f5能够找到满足精度要求的解。函数f2的全局最优在局部最优之间的谷底,检测过程中极易陷入局部最优,FA、SPSO、BA均无最佳解,而HBAFA能够寻到满足精度要求的解。综上数据分析可知,HBAFA改良了BA和FA,算法优于BA,FA和SPSO,具有更高的寻优精度,更高的稳定性,说明该算法具有一定的优越性。
2.4 鲁棒性分析标准偏差Std的大小反映了算法鲁棒性的好坏,即标准偏差越小,则算法的鲁棒性越好;反之,则算法的鲁棒性越差。由表 2的实验数据可知,在f1~f6的寻优过程中,HBAFA的标准偏差Std均小于其他3种算法的标准偏差,因此HBAFA总体的鲁棒性均优于其他3种算法。
2.5 成功率比较设定参考寻优精度值,在每一次迭代结束之后,判断适应度值是否达到目标精度10∧(-5),若达到则停止迭代,并记录一次寻优成功;若迭代次数为1 000次时仍未达到目标精度,则终止迭代。在30次独立重复试验中,4种算法的寻优成功率如表 3所示。由表 3可知,将寻优精度设置为10∧(-5),则在迭代结束后,4种算法在f2寻优成功率均为0%,而HBAFA在剩余其他5个基准函数的寻优成功率均为100%;BA、SPSO和FA的整体寻优成功率稍差。因此,在10个基准函数的寻优过程中,HBAFA总体的寻优成功率优于其他3种算法。
| Fun | HBAFA | FA | BA | SPSO |
| f1 | 100 | 0 | 0 | 0 |
| f2 | 0 | 0 | 0 | 0 |
| f3 | 100 | 0 | 0 | 0 |
| f4 | 100 | 0 | 0 | 0 |
| f5 | 100 | 0 | 0 | 0 |
| f6 | 100 | 0 | 0 | 73.3 |
2.6 算法优越性分析
HBAFA的整体性能优于其他3种算法,主要源自以下3个方面:
第一,由于蝙蝠算法具有较强的局部搜索能力,蝙蝠种群根据蝙蝠发出的脉冲和响度在全局最优个体Gbest在附近进行了更加详细的局部搜索,并提高了混合算法的收敛性能;
第二,将蝙蝠算法引入到萤火虫算法,协助萤火虫种群寻优。在寻优过程中加强了两个种群之间的信息交流,以提高种混合算法的收敛性能;
第三,在寻优过程中,对全局最优个体Gbest进行高斯扰动,提高了种群的多样性,避免种群过早地陷入局部最优。
3 结论本文通过将蝙蝠算法的局部搜索机制引入到萤火虫算法中,让蝙蝠种群协助萤火虫种群寻优;两个种群在寻优过程中加强信息交互,以提高混合算法的收敛性能;而对全局最优个体进行高斯扰动,增加了种群的多样性,避免种群过快陷入局部最优解。从萤火虫算法、标准粒子群算法、蝙蝠算法和本文提出的蝙蝠萤火虫混合算法作仿真对比实验中,可以得出这样的结论:相比其他3种算法,蝙蝠萤火虫混合算法具有相对更快的收敛速度,更高的收敛精度以及更好的鲁棒性。在未来的工作中,我们将对蝙蝠烟花混合算法进行更深入的理论研究,并将其运用到更多的具体工程实践中。
| [1] |
KENNEDY J, EBERHART R.Particle swarm optimization[C]//Proceedings of ICNN'95-International conference on Neural Networks, Ⅳ.Piscataway, NJ: IEEE Service Center, 1995: 1942—1948.
|
| [2] |
YANG X S. A new metaheuristic bat-inspired algorithm[M]. Berlin: Springer, 2010: 65-74.
|
| [3] |
YANG X S. Nature-inspired metaheuristic algorithm[M]. Beckington, UK: Luniver Press, 2010.
|
| [4] |
王艳, 王秋萍, 王晓峰. 基于改进萤火虫算法求解旅行商问题[J]. 计算机系统应用, 2018, 27(8): 219-225. |
| [5] |
ŁUCKASIK S, ŻAK S.Firefly algorithm for continuous constrained optimization task[C]//ICCCI 2009: Proceedings of the First International Conference on computational collective intelligence, semantic web, social networks and multi-agent systems, LNCS5796.Berlin: Springer, 2009: 97-100.
|
| [6] |
冯艳红, 刘建芹, 贺毅朝. 基于混沌理论的动态种群萤火虫算法[J]. 计算机应用, 2013, 33(3): 796-799, 805. DOI:10.3969/j.issn.1001-3695.2013.03.039 |
| [7] |
王吉权, 王福林. 萤火虫算法的改进分析及应用[J]. 计算机应用, 2014, 34(9): 2552-2556. |
| [8] |
GANDOMI A H, YAN X S, TALATAHARI A H, et al. Firefly algorithm with chaos[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(1): 89-98. DOI:10.1016/j.cnsns.2012.06.009 |
| [9] |
付强, 葛洪伟, 苏树智. 引入萤火虫行为和Levy飞行的粒子群优化算法[J]. 计算机应用, 2016, 36(12): 3298-3302, 3310. DOI:10.11772/j.issn.1001-9081.2016.12.3298 |
| [10] |
郝晓莹, 贺兴时, 薛菁菁. 一种粒子群-萤火虫算法的参数优化方法[J]. 西安工程大学学报, 2017, 31(5): 695-700. |
| [11] |
杜艳艳, 刘升. 一种改进的自适应混合型蝙蝠算法[J]. 微电子学与计算机, 2018, 35(6): 135-140. |
| [12] |
左仲亮, 郭星, 李炜. 一种改进的萤火虫算法[J]. 微电子学与计算机, 2018, 35(2): 61-66. |



