【研究意义】材料断裂不仅使构件完全失效,还往往产生灾难性的后果。因此,材料断裂问题,一直以来都是固体力学、断裂力学、宏微观力学等学科研究中活跃的前沿问题;然而对材料断裂过程的本质理解必须在细观力学与纳观力学的结合角度上才能实现。其中细观破坏过程的4种基本构元(孔洞、微裂纹、界面失效、变形局部化带)的起源和演化描述必须在纳观尺度才能完全阐明[1]。所以,用晶体相场(PFC)法研究纳观尺度下不同初始晶向倾角对微裂纹萌生与扩展是有非常重要的影响意义的。【前人研究进展】目前已经有许多微裂纹韧脆扩展机理的研究,其中不乏实验观测和计算模拟研究,如邢永明等[2]利用纳米云纹对Si单晶裂尖纳观变形场进行了实验研究; 张跃等[3]通过透射电子显微镜(TEM)对TiAl的原位拉伸,研究了裂尖的位错发射以及它和纳米裂纹的形核、扩展间的关系; 高克伟等[4]用带有拉伸台的高分辨电子显微镜对TiAl裂尖前端原子结构特征进行研究; Adelzadeh等[5]研究裂纹与孔洞的相互作用和韧-脆断裂转变等。相对于实验观察,计算模拟不仅能还原实验模拟现象,还便于观察实际试验中难以捕捉到的瞬时实验现象,且还能对实验结果进行预测演化模拟,因此计算机模拟是实验研究的指引与保障。作为计算模拟方法,在微裂纹研究中,晶体相场方法在扩散时间尺度和空间密度尺度上比传统相场(PFM)法和分子动力学(MD)法更具有优势[6-9]。在近几年研究中,高英俊等[10-11]在Elder等[12-13]提出的晶体相场方法模型基础上研究韧性材料的微裂纹扩展、连通与分叉,Shi等[14]用晶体相场法研究了晶界耦合运动和微裂纹的影响等。【本研究切入点】晶体相场方法作为目前较为先进的计算模拟方法,在微裂纹韧-脆转变特性上的计算模拟研究还比较少。【拟解决的关键问题】应用PFC方法研究不同初始晶向倾角样品在y方向单轴拉伸作用下的微裂纹萌生和韧-脆转变扩展规律,对材料强韧化起重要的探索、引导作用。
1 PFC模型与方法 1.1 体系的能量密度函数原始的晶体相场方法是Elder等[12-13]基于非线性斑图动力学[15-16]的Swift-Hohenberg模型[15],引入周期序参量而提出和建立的。基于经典密度泛函理论(CDFT),我们可以推导出简单的无量纲自由能函数模型,如下:
| $ F = \int {dV} \left\{ {\frac{\rho }{2}\left[ {e + {{\left( {{\nabla ^2} + 1} \right)}^2}} \right]\rho + \frac{{{\rho ^4}}}{4}} \right\}, $ | (1) |
其中,∇2是拉普拉斯算子,e为温度参数,ρ是局域原子密度[17]。在单模近似下,可求得公式(1)的一个稳定解为
| $ \rho = A\left[ {{\rm{cos}}\left( {qx} \right){\rm{cos}}\left( {\frac{{qy}}{{\sqrt 3 }}} \right)\frac{1}{2}{\rm{cos}}\left( {\frac{{2qy}}{{\sqrt 3 }}} \right)} \right] + {\rho _0}, $ | (2) |
其中,q=
采用保守场Cahn-Hilliard动力学方程[17-20]描述原子密度随时间的演化,该方程如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;\frac{{\partial \rho }}{{\partial t}} = {\nabla ^2}\frac{{\delta F}}{{\delta \rho }} + \zeta = {\nabla ^2}\{ \left[ {e + {{\left( {1 + {\nabla ^2}} \right)}^2}} \right]\rho + \\ {\rho ^3}\} + \zeta , \end{array} $ | (3) |
其中,ζ为高斯随机噪声,平均值为0。故本研究不需考虑ζ的作用。对公式(3)采用傅里叶转换方法,将实空间的数据转换到傅里叶空间中求解,再转换到实空间,最后通过MATLAB软件显示结果图像。详细求解步骤见文献[18]。
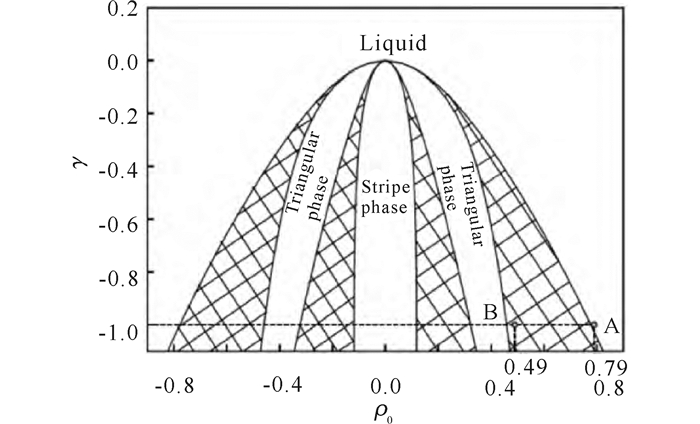
1.3 样品制备由式(2)表示的自由能极小值,可得到对应的液相、条状相和三角相3种平衡相。在二维系统中,联立三相原子密度函数和自由能公式,求解各相的自由能极小值,并利用公切线法则确定相图(图 1[19])。本研究选取原子密度参量为ρ0=0.49,温度参数e=-1.0(图 1中B点),样品中心的初始缺口为20 gp×10 gp的长方形,缺口原子密度设置为ρ1=0.79,温度参数e=-1.0(图 1中A点);计算模拟区域为1 024Δx×512Δy,Δx=Δy=
|
阴影部分代表两相共存区 The shadow parts represent the two phase coexistence region 图 1 单模近似得出的二维相图[19] Fig.1 The two-dimensional phase diagram obtained by single mode approximation[19] |
|
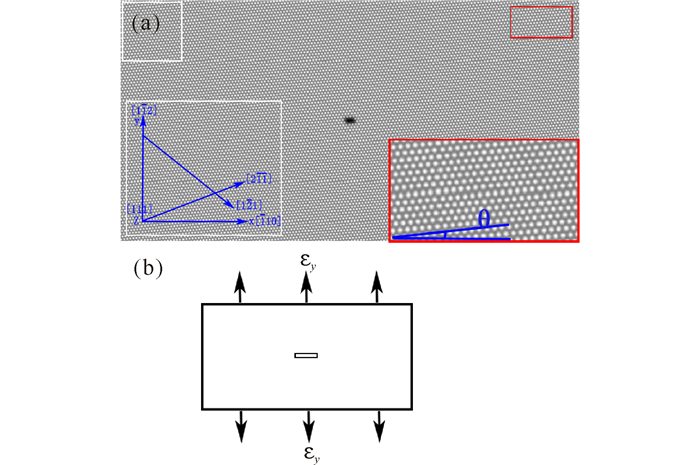
(a)初始样品:长方形初始裂口的实验坐标体系;(b)初始晶向倾角为θ的样品y方向施加应变 (a)Initial sample:Experimental coordinate system of rectangular initial crack; (b)Strain applied in the y direction of the sample with an initial crystal tilt angle of θ 图 2 实验坐标体系与y方向应变施加 Fig.2 Experimental coordinate system and y direction strain application |
| 表 1 4组不同初始晶向倾角的裂口样品参数 Table 1 Parameters of crack samples of 4 groups with different initial crystal orientation angles |
为研究不同初始晶向倾角对裂纹的萌生和扩展的影响,经过50 000步弛豫后,得到含缺口的稳定样品(图 2a,其放大区域给出实验的坐标体系),再分别对4个弛豫后的样品y轴方向施加500 000步拉应变(图 2b所示);由于在拉应变作用下前60 000步为应力释放阶段,故本研究对此阶段不做考虑,仅研究60 000~500 000步间过程。在变形过程中,样品y轴方向每一时间步长应变增加量为ε=
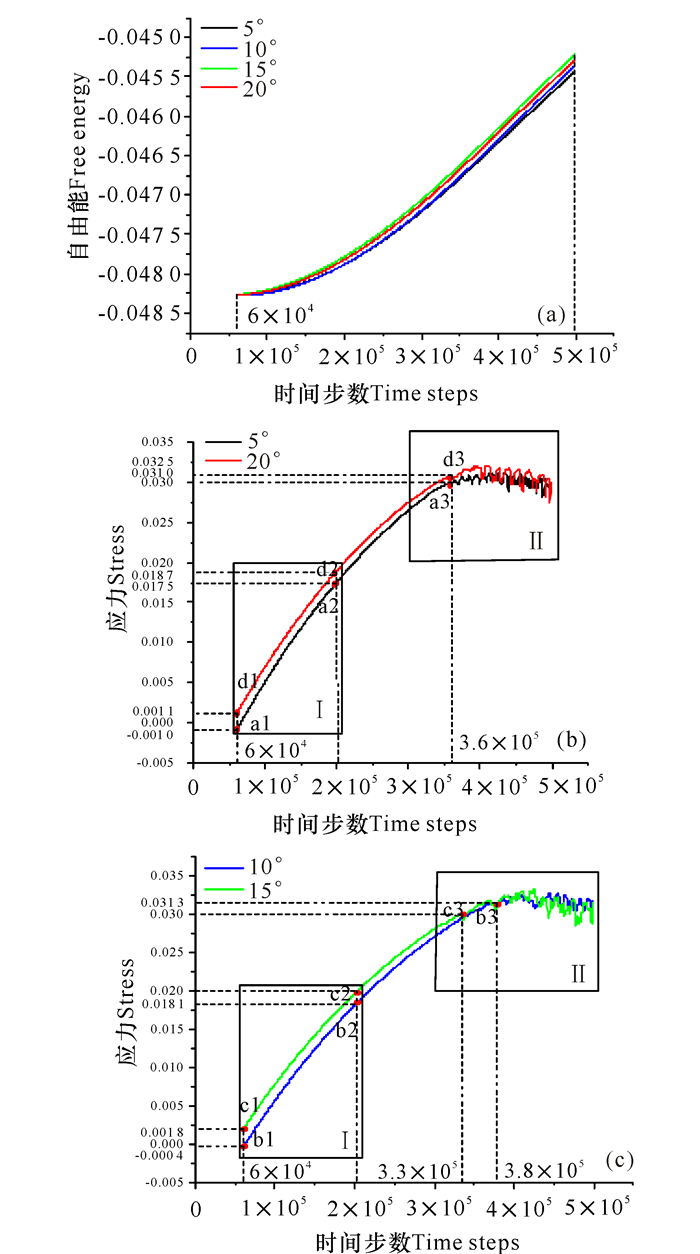
在外应变的作用下,A、B、C、D 4个样品的系统平均自由能不断增大,能量变化基本一致(图 3a)。通过能量对应变的求导,得到应力-时间曲线(图 3b~c),其中将近似于线性增长的应力-时间曲线的60 000~200 000步部分定义为Ⅰ部分,将应力-时间曲线300 000~500 000步的波动部分定义为Ⅱ部分。
|
(a)自由能随时间变化曲线;(b)初始晶向倾角为5°与20°的应力-时间曲线;(c)初始晶向倾角为10°与15°的应力-时间曲线 (a)Free energy versus time curve; (b) Stress-time curve with initial crystal orientation inclination of 5° and 20°; (c) Stress-time curve with initial crystal orientation inclination of 10° and 15° 图 3 自由能-时间曲线与应力-时间曲线 Fig.3 Free energy-time curve and stress-time curve |
样品在500 000步y方向的拉应变作用下,表现出了弹性形变和塑形形变行为。开始阶段,样品A、B、C、D所受外应力类似于线性增长(图 3b~c中Ⅰ部分),此时,样品主要表现出弹性变形行为;图 3中Ⅱ部分应力曲线随时间的波动,主要体现了样品塑性变形行为,其中a3、b3、c3、d3分别对应着样品A、B、C、D裂纹萌生的临界时刻:360 000步、380 000步、330 000步、360 000步,对应的应变值分别为εy=10.8%、11.4%、9.9%、10.8%。当时间步数t=500 000时,即应变量εy=15%,裂纹韧脆扩展形貌基本完成(图 4),其中图 4a、b、c、d分别对应样品A、B、C、D在t=500 000步时的裂纹扩展演化图;图 4a和图 4d主要表现为样品A、D中裂纹的脆性扩展行为,图 4b和图 4c主要表现出样品的B、C中裂纹的韧性扩展行为。裂尖处位错的运动的方式,决定了裂纹扩展的行为。

|
左图为t=500 000步时的裂纹扩展形貌,右图为对应的应力分布 The left picture shows the crack propagation morphology at t=500 000 steps, and the right picture shows the corresponding stress distribution 图 4 样品A、B、C、D的裂纹扩展形貌 Fig.4 Crack propagation morphology of samples A, B, C, D |
由表 1知样品A初始晶向倾角为5°,在图 4a中,裂纹边缘呈光滑状,左右两端裂尖位置处各存在一对位错锁。由于裂尖应力集中,裂纹沿着位错锁滑移的矢量和方向扩展,即裂纹左右两尖端分别沿着[110]和[110]方向扩展延伸,这是典型脆性解理裂纹扩展模式。当初始晶向倾角为20°时,由图 4d可见,裂纹初始扩展时,边缘呈光滑状,裂纹左右两边扩展方向为沿偏[121]和偏[121]晶向与水平方向夹角为40°方向;由于裂尖位错锁矢量和的滑移方向受阻,裂尖应力集中,裂尖钝化,前进转向,裂纹边缘呈锯齿状,沿着偏[110]和[110]晶向与水平方向夹角为20°方向扩展,锯齿状裂纹与初始边缘光滑裂纹夹角呈120°,且裂纹右边扩展经过多次转向后,沿初始方向[121]继续扩展,即裂纹左边扩展形貌为光滑-锯齿,右边扩展形貌为光滑-锯齿-光滑,但主裂纹扩展模式仍然为脆性扩展。同时对两脆性扩展裂纹的应力-时间曲线分析:在拉应变作用下,裂口应力集中,应力-时间曲线呈上升趋势,达到临界应力a3、d3时,裂纹开始萌生,且两脆性裂纹的萌生时间相同,为t=360 000步,对应图 3b中a3、d3点时刻;当应力达到裂纹萌生的临界值a3、d3后,应力-时间曲线随着脆性裂纹扩展而波动(图 3b中Ⅱ部分)。
2.3 初始晶向倾角为10°、15°的裂纹扩展图 4b~c为典型的韧性裂纹扩展模式,裂纹随着裂尖位错发射、滑移运动而扩展延伸,裂尖位错克服原子间势垒做滑移运动的原子层数与图 3c中Ⅱ部分应力随时间波动的峰苞或者谷苞有密切关系。由于裂纹尖端应力集中,裂尖发射位错,位错滑移,形成一系列空位,空位长大形成孔洞,空洞连通,与主裂纹接连,形成裂纹,若不与主裂纹连通,则形成二次裂纹,裂纹边缘为锯齿状。结合图 3c和图 4b~c可知,10°、15°初始晶向倾角样品中的裂纹都呈韧性扩展模式,但裂纹萌生时间和扩展方向、形式都有所差异。在图 4b中,裂纹左右两端分别沿偏[121]和偏[121]晶向与水平方向夹角呈10°方向扩展,且裂尖位错滑移仅形成一个空位,空位长大形成空洞,与主裂纹连通;而在图 4c中,主裂纹左右两端分别沿偏[121]和偏[121]晶向与水平方向夹角呈30°方向扩展,且裂尖与远端位错滑移处皆出现应力集中现象,此时裂尖处可能出现转向扩展,远端位错滑移形成多处空位,空位长大连通形成空洞,空洞连接成为裂纹。通过应力-时间曲线(图 3c)研究分析,裂纹萌生之前,在拉应变作用下,裂口应力集中,应力-时间曲线上升;当裂口达到临界应力b3、c3时,开始发射位错。10°、15°初始晶向倾角裂口开始发射位错各为b3、c3点对应的两个不同时刻,分别为t=380 000步、330 000步;当应力达到裂纹萌生的临界值b3、c3后,应力-时间曲线随着韧性裂纹扩展而波动(图 3c中Ⅱ部分)。
3 结论初始晶向夹角为5°、20°的样品,在y轴方向拉应变作用下,裂纹扩展形式为脆性扩展模式,初始晶向夹角为10°、15°的样品,在y轴方向拉应变作用下,裂纹扩展形式为韧性扩展模式。
初始晶向夹角为5°到20°的样品,在y轴方向拉应变作用下,改变样品初始晶向夹角,会影响到裂口裂纹萌生时间、裂纹扩展方向以及韧-脆扩展形式。
| [1] |
杨卫.宏观断裂力学[M].国防工业出版社, 1995: 290-301. YANG W.Macroscopic and microscopic fracture mechanics[M]. National Defense Industry Press, 1995: 290-301. |
| [2] |
邢永明, 戴福隆, 杨卫. 准解理微裂纹裂尖纳观变形场的实验研究[J]. 中国科学:A辑, 2000, 30(8): 49-54. XING Y M, DAI F L, YANG W. Experimental study on the deformation field of quasi-cleavage microcrack crack tip[J]. Science in China:Series A, 2000, 30(8): 49-54. |
| [3] |
张跃, 褚武扬, 王燕斌, 等. 金属间化合物脆性微裂纹的TEM观察[J]. 中国科学:A辑, 1994, 24(5): 551-560. ZHANG Y, CHU W Y, WANG Y B, et al. TEM observation of brittle microcracks of intermetallic compounds[J]. Science in China:Series A, 1994, 24(5): 551-560. |
| [4] |
高克伟, 陈奇志, 褚武扬, 等. 纳米级解理微裂纹的形核与扩展[J]. 中国科学:A辑, 1994, 24(10): 993. GAO K W, CHEN Q Z, CHU W Y, et al. Nucleation and extension of nanoscale cleavage microcracks[J]. Science in China:Series A, 1994, 24(10): 993. |
| [5] |
ADELZADEH M, SHODJA H M, RAFⅡ-TABAR H. Computational modeling of the interaction of two edge cracks, and two edge cracks interacting with a nanovoid, via an atomistic finite element method[J]. Computational Materials Science, 2008, 42(2): 186-193. DOI:10.1016/j.commatsci.2007.07.012 |
| [6] |
RAPAPORT D C. The art of molecular dynamics simulation[M]. 2nd ed. New York: Cambridge University Press, 1995.
|
| [7] |
STEINBACH I. Phase-field model for microstructure evolution at the mesoscopic scale[J]. Annual Review of Materials Research, 2013, 43(1): 89-107. DOI:10.1146/annurev-matsci-071312-121703 |
| [8] |
CHEN L Q. Phase-field models for microstructure evolution[J]. Annual Review of Materials Research, 2002, 16(32): 113-140. |
| [9] |
高英俊, 卢昱江, 孔令一, 等. 晶体相场模型及其在材料微结构演化的应用[J]. 金属学报, 2018, 54(2): 278-292. GAO Y J, LU Y J, KONG L Y, et al. Phase field crystal model and its application for microstructure evolution of materials[J]. Acta Metallurgica Sinica, 2018, 54(2): 278-292. |
| [10] |
高英俊, 罗志荣, 邓芊芊, 等. 韧性材料的微裂纹扩展与分叉的晶体相场模拟[J]. 计算物理, 2014, 31(4): 471-478. GAO Y J, LUO Z R, DENG Q Q, et al. Phase-field-crystal modeling of microcrack propagation and branching in ductile materials[J]. Chinese Journal of Computational Physics, 2014, 31(4): 471-478. DOI:10.3969/j.issn.1001-246X.2014.04.013 |
| [11] |
高英俊, 罗志荣, 黄世叶, 等. 韧性材料的微裂纹扩展和连通的晶体相场模拟[J]. 中国有色金属学报, 2013, 23(7): 1892-1899. GAO Y J, LUO Z R, HUANG S Y, et al. Phase-field-crystal modeling for microcrack propagation and connecting of ductile materials[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(7): 1892-1899. |
| [12] |
ELDER K R, KATAKOWSKI M, HAATAJA M, et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88(24): 245701. DOI:10.1103/PhysRevLett.88.245701 |
| [13] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70(5Pt1): 051605. |
| [14] |
SHI H, WEN X, ZHENG C, et al. Coupled motion of grain boundaries and the influence of microcracks:A phase-field-crystal study[J]. Computational Materials Science, 2017, 132: 125-131. DOI:10.1016/j.commatsci.2017.02.021 |
| [15] |
CROSS M, GREENSIDE H. Pattern formation and dynamic in nonequilibrium systems[M]. Cambridge: Cambridge University Press, 2009: 1.
|
| [16] |
PROVATAS N, ELDER K. Phase-field methods in materials science and engineering[M]. Weinheim: Wiley-VCH, 2010: 1.
|
| [17] |
高英俊, 黄礼琳, 周文全, 等. 高温应变下的亚晶界湮没与位错旋转机制的晶体相场模拟[J]. 中国科学:技术科学, 2015, 45(3): 306-321. GAO Y J, HUANG L L, ZHOU W Q, et al. Phase field crystal simulation of subgrain boundary annihilation and dislocation rotation mechanism under strain at high temperature[J]. Scientia Sinica:Technologica, 2015, 45(3): 306-321. |
| [18] |
卢昱江, 孔令一, 邓芊芊, 等. 微裂纹起裂扩展机理的晶体相场模拟[J]. 广西科学院学报, 2017, 33(4): 240-245. LU Y J, KONG L Y, DENG Q Q, et al. Phase field crystal simulation of nucleation and propagation of micro-cracks[J]. Journal of Guangxi Academy of Sciences, 2017, 33(4): 240-245. |
| [19] |
黄礼琳, 叶里, 胡绪志, 等. 不同晶向取向的裂纹扩展演化模拟[J]. 广西科学, 2016, 23(5): 454-458, 469. HUANG L L, YE L, HU X Z, et al. Simulation study of crack propagation and evolution in different crystal orientations[J]. Guangxi Sciences, 2016, 23(5): 454-458, 469. |
| [20] |
高英俊, 卢成健, 黄礼琳, 等. 晶界位错运动与位错反应过程的晶体相场模拟[J]. 金属学报, 2014, 50(1): 110-120. GAO Y J, LU C J, HUANG L L, et al. Phase field crystal simulation of dislocation movement and reaction[J]. Acta Metallurgica Sinica, 2014, 50(1): 110-120. |
 2018, Vol. 34
2018, Vol. 34 


