【研究意义】晶体材料通常由大量晶粒组成,晶界是结构相同而取向不同晶粒之间的界面。根据相邻晶粒位相差的大小,可把晶界分为小角晶界和大角晶界两种类型。小角晶界又可分为一般小角晶界、对称倾侧晶界和扭转晶界,其中对称倾侧晶界和扭转晶界是小角晶界的特殊形式。晶界是由多组Burgers矢量不同位错按一定的方式循环排列组成。晶界位错的存在造成其周围的原子点阵排列畸变。在稳定的环境条件下,晶界(包括亚晶界)可以保持稳定的结构,对晶体持续施加应变会导致晶界位错迁移、增殖和湮没。位错演化是理解晶体材料和结构的可塑性、破坏和破坏的关键的微观事件[1]。通过观察晶界分裂过程中晶体表面原子的运动情况,分析晶界位错的结构组态演化及其涉及的位错反应,对晶粒长大特别是对冷加工金属材料的退火有重要意义[2]。【前人研究进展】晶体相场(PFC)模型是用于研究在原子尺度和扩散时间尺度上发生的现象的模拟方法[3]。PFC模型是通过分析自由能来进行模拟的,该自由能代表固体结晶相的周期性有序参数分布或液相的恒定阶参数分布的最小值[4-5]。因此PFC模型可以描述非平衡过程中的弹性和塑性变形,多晶体取向和自由表面[5]。该模型已在国际上被用于研究许多重要的材料现象,如国内高英俊课题组对位错运动[6-9]、裂纹扩展[10]、结构相变[11]的研究,国外Gránásy等[12]对成核、晶体外延生长[13]、凝固[14-15]和晶界能量各向异性[5, 16]的研究。基于密度泛函理论模型提出的PFC方法,相比于分子动力学方法其优势在于可以在扩散时间尺度(10-6 s)对纳米尺度的缺陷运动进行模拟分析。对比传统相场方法[17-18],PFC方法在可以研究纳米尺度材料微结构的同时,还能够研究扩散时间尺度的晶界位错结构组态的演化过程。【本研究切入点】晶界位错的组态演化过程是非常快速的,在目前的实验条件下,难以清晰地在纳米尺度观察到其位错的迁移、增殖和湮没过程,因此通过PFC模型进行计算机模拟实验的优势就尤为突出。PFC方法能够很好地描述在施加应变的作用下晶界位错在扩散时间尺度上的运动情况[19]。分析高温应变下晶界位错的位错反应能够更加直接地揭示位错运动的方向并从能量角度解释位错增殖和湮没的原因。【拟解决的关键问题】应用晶体相场(PFC)方法模拟高温下对晶体持续施加应变晶体的位错结构的组态演化,从位错反应方面分析晶界位错的迁移、增殖和湮没过程。
1 模型与方法 1.1 PFC模型参考文献[20],用原子密度函数表示相场变量,表达式为
| $ \rho \left( r \right) = \sum\limits_{n, m} {{a_{n, m}}{e^{iG \cdot r}} + {\rho _0}, } $ | (1) |
式中an, m为Fourier系数,G为倒格矢,r为空间位置矢量。式(1)中等式右边第一项表示晶格原子的周期排列结构特征,第二项ρ0代表原子平均密度,表示液相的原子均匀无序特征,平均值为常量。此时体系无量纲的自由能函数F可以写成
| $ F = \int {\left\{ {\frac{\rho }{2}\left[ {\gamma + {{\left( {1 + {\nabla ^2}} \right)}^2}} \right]\rho + \frac{{{\rho ^4}}}{4}} \right\}{\rm{d}}r, } $ | (2) |
式(2)中,γ代表体系温度的参数,
| $ \begin{array}{l} \;\;\;\;\;\;\rho \left( {x, y} \right) = {A_0}[{\rm{cos}}\left( {qx} \right){\rm{cos}}\left( {\frac{{qy}}{{\sqrt 3 }}} \right) - \\ \frac{1}{2}{\rm{cos}}\left( {\frac{{2qy}}{{\sqrt 3 }}} \right)] + {\rho _0}, \end{array} $ | (3) |
式(3)中,波矢q=
由式(2)得到的自由能极小值,可以得到对应的3种平衡相,即液相(Liquid),条状相(Stripe)和三角相(Triangular)。以此获得在二维体系中各相平衡时的自由能密度,再利用自由能公切线法确定相图[22]。
1.2 模拟实验的样本设计由于分析真实的纳米级晶粒中的三位缺陷结构所需要了解的因素和参数太多,目前难以分析,且高分辨电镜实验直接观察到的变形机理,通常都涉及到具有柱状晶的二维纳米晶薄膜,还有大量实验表明纳米晶体材料的塑性变形行为与薄膜材料的变性行为十分相似。故为了便于分析,本次模拟实验采用FCC(face centered cubic)晶格的{111}平面作为基础结构体系。
我们制备的样品长宽为Lx×Ly=2 048Δx× 1 024Δy,尺度约为120 nm×60 nm,双晶结构,设置周期边界条件。将样品划分为3个矩形区域:0 < x≤Lx/4,Lx/4 < x < 3Lx/4,3Lx/4≤x < Lx。设定0 < x≤Lx/4和3Lx/4≤x < Lx区域的原子排列方向与水平线的法线夹角为2.5°,Lx/4 < x < 3Lx/4区域内的原子取向角为-2.5°,样品中原子均以六角结构排列。得到单相双晶结构的样本晶界取相差为5°。再通过将样品弛豫一段时间,最终形成稳定匹配的晶界。
1.3 施加应变对制得的高温样品分别沿其x轴方向和y轴方向持续施加应变率
| $ S = \Delta x\Delta y = \Delta x' \Delta y' , $ |
式中,Δx和Δy为初始空间步长,Δx′和Δy′是变形后的空间步长。经过时间步数n后,空间步长为[18]
| $ \begin{array}{l} \Delta x' = \Delta x/\left( {1 + n\;\dot \varepsilon \Delta t} \right), {\rm{ }}\\ \Delta y' = \Delta y/\left( {1 + n\;\dot \varepsilon \Delta t} \right), \end{array} $ |
更加具体的二维拉伸变形模拟的数值算法可详见文献[22]。
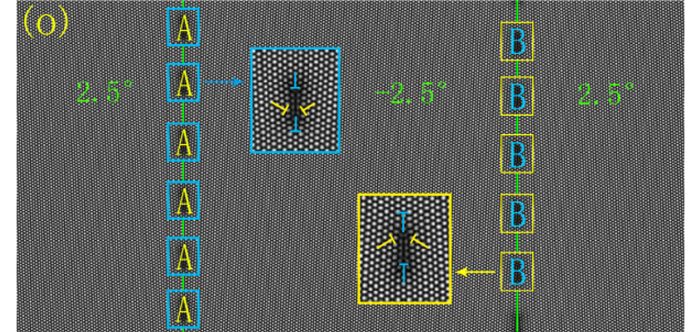
2 结果与分析 2.1 预熔化样品的晶界位错结构弛豫24 300步制备得到高温样品如图 1所示。样品中有两列位错构成了2.5°角等倾对称晶界。晶界由结构相似的4个晶格位错组成一组特殊的结构重复竖直排列组成。图 1中绿色实线处为双晶样品的晶界。左侧晶界由A类位错组成,共6组。不完整的位错组并没有在图中画出,由于制备样品时设置了周期边界条件,所以右侧晶界也是由6组B类位错组成。如图 1中蓝色方框所示,中间两个蓝色刃型位错(以下均简称位错)竖直排列,两个黄色位错对称分布在两侧,Burgers矢量夹角大致呈120°。不同列的晶界位错Burgers矢量彼此相反,但每组位错的排列方式和相对位置相同。从图中可以看出高温样品中的位错周围出现明显的黑色预熔化区域,预熔化区域中的位错结构还能够清晰地辨认出来,表明该区域固相结构仍然坚固。位错的存在使晶体处于高能的不稳定状态。
|
图 1 样品初始晶界位错形貌 Fig.1 The dislocation topography of the grain boundary of original sample |
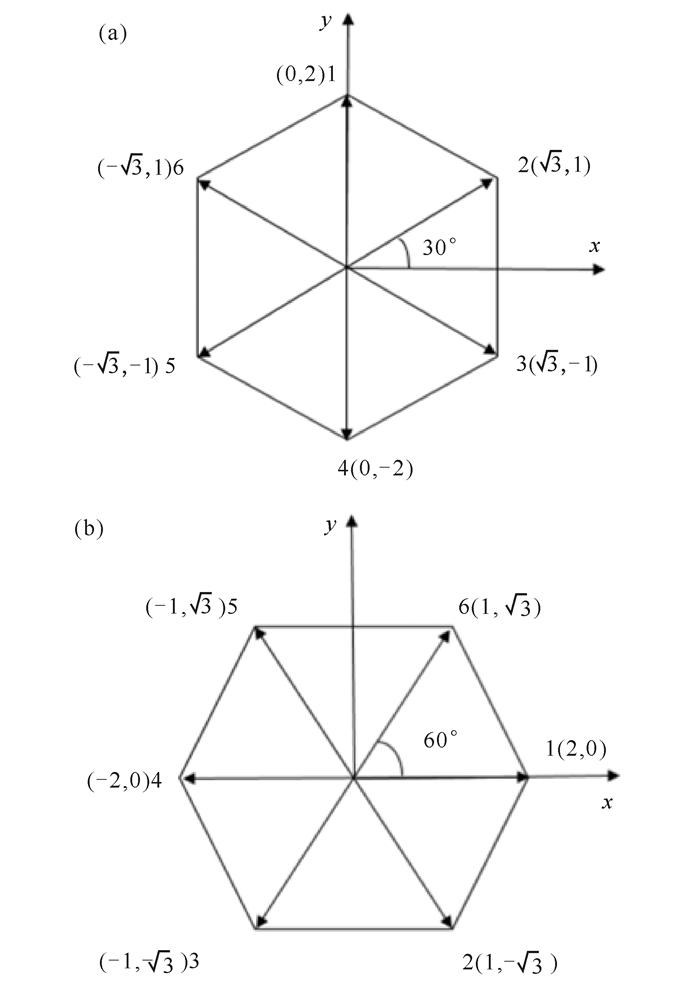
对于二维三角晶体原子排列的平面,在设置原子密度参数为0.194和温度参数为-0.10的初始对称倾侧晶界结构如图 1所示。本文模拟的二维三角晶体格子的原子排列方向与x轴的夹角φ=0。根据文献[23],此时样品中刃位错的方向只有6个可能,图 2a给出了所有可能的6个刃位错多余半原子面。刃位错Burgers矢量的方向与位错方向垂直,图 2b给出了相对应的6个刃位错的Burgers矢量的方向。其位错Burgers矢量如下:
| $ \begin{array}{l} \;\;\;\;{b_1} = a\left( {\frac{1}{2}y + \frac{{\sqrt 3 }}{2}x} \right);{b_2} = a\left( { - \frac{1}{2}y + \frac{{\sqrt 3 }}{2}x} \right);\\ {b_3} = - ay;{b_4} = - a\left( {\frac{1}{2}y + \frac{{\sqrt 3 }}{2}x} \right);{b_5} = a\left( {\frac{1}{2}y - \frac{{\sqrt 3 }}{2}x} \right);\\ {b_6} = ay。\end{array} $ |
|
图 2 二维三角晶体中刃位错的多余原子面的原子排列方向和对应的刃位错的Burgers矢量的方向 Fig.2 The direction of the atomic arrangement of the excess atomic plane of the blade dislocation in the two-dimensional triangular crystal and the direction of the Burgers vector of the corresponding edge dislocation |
式中,x和y分别是在x方向和y方向上的单位矢量,a是原子间距。如图 2b可知,全部6个方向的Burgers矢量可以用其中2个基本的Burgers矢量方向b1和b2组合表示出来,如:b3=b2-b1; b4=-b1; b5=-b2; b6=b1-b2。
假设可以忽略应力作用引起的原子排列晶格畸变的影响,现定义图 2给出的位错多余原子面可能的6个方向为Hi,则与其对应的Burgers矢量为bi。
对制得的高温样品分别沿其x轴方向和y轴方向持续施加应变率大小为1.6×10-7的拉应变和压应变,样品晶界上的位错增殖和湮没过程如图 3所示。由于在位错反应的全部过程中,样品的左侧晶界和右侧境界上位错的变化除方向相反外其余皆相同,且本样品中位错数量较多,位错反应较为复杂,为精简语言缩短篇幅,故以下只详细分析讨论样品的左侧晶界,右侧境界的位错变化可以参考左侧。
|
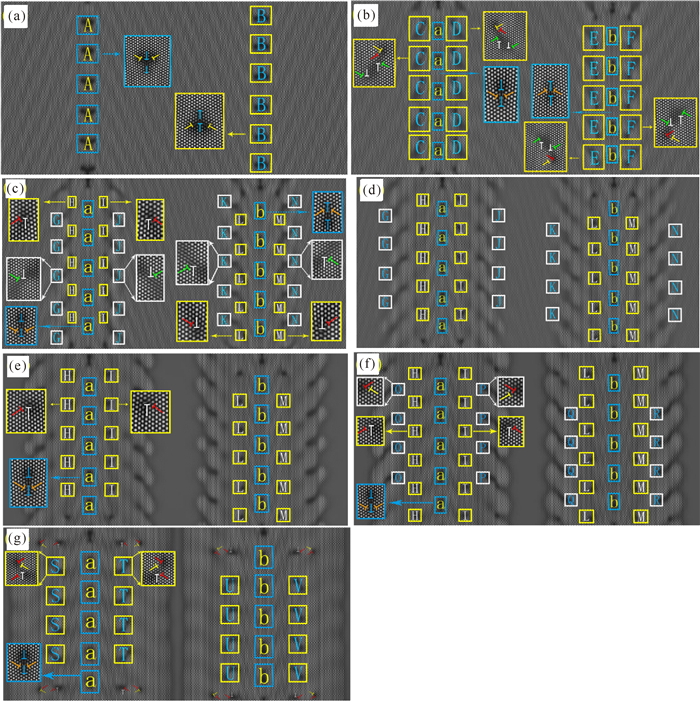
各图对应的应变量:(a)0.048 5;(b)0.070 3;(c)0.073 4;(d)0.079 7;(e)0.082 8;(f)0.086 4;(g)0.095 3 The corresponding strain:(a)0.048 5;(b)0.070 3;(c)0.073 4;(d)0.079 7;(e)0.082 8;(f)0.086 4;(g)0.095 3 图 3 高温样品在应变作用下的晶界位错结构组态变化 Fig.3 The configuration change of the dislocation structure of grain boundary of the high temperature sample under strain |
由图 3a和图 3b可知,在3a到3b的过程中样品晶界上发生了位错增殖,此时在持续施加应变的作用下,左侧晶界上分布在两侧的黄色位错分别向左上和右上逐渐远离晶界移动。直至脱离图 3a中的A位错组与新增殖出的红色位错组成新的位错对,同时,还增殖出两对Burgers矢量方向相反白绿位错对。以下定义b1~b6为位错b1~b6的Burgers矢量,图 3方框中字母A、a、B、b、G、H、I、J、K、L、M、N、O、P、Q、R、S、T、U、V代表的位错对的Burgers矢量和分别为A、a、B、b、C、D、E、F、G、H、I、J、K、L、M、N、O、P、Q、R、S、T、U、V。则图 3b中的C、a、D方框中位错对Burgers矢量和为
| $ \begin{array}{l} \;\;\;\;\;\;\;a = {b_1} + {b_1} + {b_2} + {b_6}, C = {b_1} + {b_6} + {b_3} + {b_4} + \\ {b_5} + {b_6}, D = {b_4} + {b_5} + {b_1} + {b_2} + {b_2} + {b_3}。\end{array} $ |
由于b1=-b4,b2=-b5,b3=-b6,故C+D=0,由此可知,位错发生增殖时,其本质是产生了分布于晶界两侧的对称位置数量相等且Burgers矢量总和为0的多组位错对。由C=b5+b6,D=b2+b3,C=-D可知,在晶界处增殖出的位错对,左侧位错对和右侧位错对的Burgers矢量之分别不为0,并且方向相反。
根据图 3b和图 3c可知,此时,图中的红黄位错对和右侧的白绿位错对彼此靠近至接触,Burgers矢量相反的黄色和绿色位错互相抵消湮没,余下的红色和白色位错结合成新的位错对(H和I)沿着原红黄位错对和右侧白绿位错对运动方向的矢量和方向运动,位错的数量减少。过程中发生的位错反应为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;H = {b_3} + {b_4} + {b_5} + {b_6} = {b_4} + {b_5}, I = {b_4} + {b_5} + \\ {b_2} + {b_3} = {b_3} + {b_4}。\end{array} $ |
在图 3b至图 3c的过程中,在高温应变的作用下发生晶界分裂,经过了位错发射、增殖、合并的过程后,分裂出的位错对与新增殖出的位错对合并得到H、I,H和I基本稳定在图 3c中的位置,无较大移动。G和J并不是通过晶界分裂产生的两列位错对,而是仅通过位错增殖得到的。
根据图 3d和3e可知,在对样品持续施加恒定应变率的拉应变和压应变至ε=0.079 7时,由晶粒中间处开始原子颜色变深,此处样品温度快速升高,即出现了大面积具有预熔化特征的区域,此时预熔化区域的原子排列依然整齐有序,位错结构清晰可见,即该区域固相结构仍然稳定。此时图 3d中的在晶界两侧的白绿位错对分别沿着-G和-J方向滑移至晶粒内部的预熔化区域直至位错在晶粒内部湮没。对此本文认为,左侧晶界的J和右侧晶界的K进入晶粒内部时其能量被晶粒吸收,促进了预熔化区域的扩张,原子排列无序混乱,原固相结构变软熔化,更接近于液相,则位错对在半液半固的晶体内部中湮没。J和K具有方向相反的Burgers矢量,互相吸引,K=b4+b5。故此过程可以看成发生了位错反应:
| $ J + K = {b_1} + {b_2} + {b_4} + {b_5} = 0。$ |
图 3f和图 3g中Burgers矢量分别为O=b2+b3,P=b5+b6。晶粒中心区域向两侧晶界发射位错对,而其自身的面积则逐渐减小,且彻底成为液相,此时已经完全无法分清单个原子(图 3f~g)。根据O+P=b2+b3+b5+b6=0可知,液相区域向晶界发射了两种Burgers矢量相反的位错对。因为红白位错对(H、I)和红黄位错对(O、P)中的红色位错Burgers矢量方向相反,故相互吸引使彼此靠近。图 3g中部分位错对排列并不是很整齐,本文认为是由于应变量过大,导致样品各处能量分布没有完全均匀,故出现位错对迁移速率不一致的现象,在此对这种现象暂不讨论,在后续工作和研究中会对此类现象进行分析和讨论。结合对图 3a~e的分析发现,在位错增殖和湮没的过程中,样品的总Burgers矢量是守恒的,总是等于原始晶界处的位错组A的Burgers矢量。
在图 3g后的样品,即应变量大于0.095 3之后,在样品各处出现大量无规则分布的位错。对应的宏观现象为实验样品在高温应变下断裂,故之后的现象无实际意义,不对其进行分析讨论。
3 结论在高温应变的作用下,晶体会发生晶界分裂现象,分裂出的晶界位错对与增殖出的位错对发生位错反应,能量降低,结构趋于稳定,得到的新位错对的位置稳定在晶界两侧基本无变化。发生增殖时,本质是产生了分布于晶界两侧的对称位置数量相等且Burgers矢量总和为0的多组位错对。在晶界处增殖出的位错对,左侧位错对和右侧位错对的Burgers矢量之和分别不为0,并且方向相反。在位错增殖和湮没的过程中,样品的总Burgers矢量是守恒的,总是等于初始晶界处的位错组A的Burgers矢量。
| [1] |
SHUANG F, XIAO P, KE F J, et al. Efficiency and fidelity of molecular simulations relevant to dislocation evolutions[J]. Computational Materials Science, 2017, 139: 266-272. DOI:10.1016/j.commatsci.2017.07.044 |
| [2] |
HAYAKAWA M, YAMAGUCHI K, KIMURA M, et al. Visualization of subgrain structure for a ferritic 12Cr-2W steel using backscattered scanning electron microscopy[J]. Materials Letters, 2004, 58(21): 2565-2568. DOI:10.1016/j.matlet.2004.03.003 |
| [3] |
CHAN V W L, PISUTHA-ARNOND N, THORNT-ON K. Thermodynamic relationships for homogeneous crystalline and liquid phases in the phase-field crystal model[J]. Computational Materials Science, 2017, 135: 205-213. DOI:10.1016/j.commatsci.2017.04.017 |
| [4] |
ELDER K R, KATAKOWSKI M, HAATAJA M, et al. Modeling elasticity in crystal growth[J]. Phys Rev Lett, 2002, 88(24): 245701. DOI:10.1103/PhysRevLett.88.245701 |
| [5] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Phys Rev E Stat Nonlin Soft Matter Phys, 2004, 70(5): 051605. DOI:10.1103/PhysRevE.70.051605 |
| [6] |
杨瑞琳, 刘瑶, 胡绪志, 等. 双位错滑移运动的晶体相场模拟[J]. 广西科学, 2016, 23(5): 443-447. YANG R L, LIU Y, HU X Z, et al. Phase-field-crystal simulation of double dislocation gliding[J]. Guangxi Sciences, 2016, 23(5): 443-447. |
| [7] |
高英俊, 黄礼琳, 周文权, 等. 高温应变下的亚晶界湮没与位错旋转机制的晶体相场模拟[J]. 中国科学, 2015, 45(3): 306-321. GAO Y J, HUANG L L, ZHOU W Q, et al. Phase field crystal simulation of subgrain boundary annihilation and dislocation rotation mechanism under strain at high temperature[J]. Sci Sin Tech, 2015, 45(3): 306-321. |
| [8] |
高英俊, 卢成建, 罗志荣, 等. 晶界位错发射与湮没过程的晶体相场模拟[J]. 中国有色金属学报, 2014, 24(8): 2073-2082. GAO Y J, LU C J, LUO Z R, et al. Phase field crystal simulation of dislocation emission and annihilation at grain boundary[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(8): 2073-2082. |
| [9] |
高英俊, 卢成健, 黄礼琳, 等. 晶界位错运动与位错反应过程的晶体相场模拟[J]. 金属学报, 2014, 50(1): 110-120. GAO Y J, LU C J, HUANG L L, et al. Phase field crystal simulation of dislocation movement and reaction[J]. Acta Metallurgiga Sinica, 2014, 50(1): 110-120. |
| [10] |
毛鸿, 罗志荣, 黄世叶, 等. 材料裂纹扩展分叉机理的晶体相场法研究[J]. 广西科学, 2015, 22(5): 499-505. MAO H, LUO Z R, HUANG S Y, et al. Phase-field-crystal modeling for crack propagation and branch of materials[J]. Guangxi Sciences, 2015, 22(5): 499-505. DOI:10.3969/j.issn.1005-9164.2015.05.008 |
| [11] |
高英俊, 罗志荣, 黄创高, 等. 晶体相场方法研究二维六角相向正方向结构转变[J]. 物理学报, 2013, 62(5): 050507. GAO Y J, LUO Z R, HUANG C G, et al. Phase-field-crystal modeling for two-dimensional transformation from hexagonal to square structure[J]. Acta Physica Sinsca, 2013, 62(5): 050507. |
| [12] |
GRÁNÁSY L, TEGZE G, TÓTH G, et al. Phase-field crystal modelling of crystal nucleation heteroepitaxy and patterning[J]. Philosophical Magazine, 2011, 91(1): 123-149. DOI:10.1080/14786435.2010.487476 |
| [13] |
ELDER K R, ROSSI G, KANERVA P, et al. Patterning of heteroepitaxial overlayers from nano to micron scales[J]. Phys Rev Lett, 2012, 108: 226102. DOI:10.1103/PhysRevLett.108.226102 |
| [14] |
ASADI E, ZAEEM M A. Quantitative phase-field crystal modeling of solid-liquid interfaces for FCC metals[J]. Computation Materials Science, 2017, 127: 236-243. DOI:10.1016/j.commatsci.2016.11.005 |
| [15] |
NOURIAN-AVVAL A, ASADI E. On the quantification of phase-field crystals model for computational simulations of solidification in metals[J]. Computation Materials Science, 2017, 128: 294-301. DOI:10.1016/j.commatsci.2016.11.042 |
| [16] |
BERRY J, ELDER K R, GRANT M. Simulation of an atomistic dynamic field theory for monatomic liquids:Freezing and glass formation[J]. Physical Review E, 2008, 77: 061506. DOI:10.1103/PhysRevE.77.061506 |
| [17] |
陈云, 康秀红, 李殿中. 自由枝晶生长相场模型的自适应有限元法模拟[J]. 物理学报, 2009, 58(1): 390-398. CHEN Y, KANG X H, LI D Z. Phase-field modeling of free dendritic growth with adaptive finite element method[J]. Acta Physica Sinaca, 2009, 58(1): 390-398. DOI:10.3321/j.issn:1000-3290.2009.01.060 |
| [18] |
高英俊, 罗志荣, 黄礼琳, 等. 变形合金的亚晶组织演化的相场模型[J]. 金属学报, 2012, 48(10): 1215-1222. GAO Y J, LUO Z R, HUANG L L, et al. Phase field model for microstructure evolution of subgrain in deformation alloy[J]. Acta Metallurgiga Sinica, 2012, 48(10): 1215-1222. |
| [19] |
叶里, 胡绪志, 黄礼琳, 等. 拉应力作用下晶界位错运动过程的晶体相场模拟[J]. 广西科学, 2016, 23(5): 470-473, 484. YE L, HU X Z, HUANG L L, et al. Phase-field-crystal simulation of grain boundary dislocation motion under tensile stress[J]. Guangxi Sciences, 2016, 23(5): 470-473, 484. |
| [20] |
黄世叶, 刘晓骅, 谢森, 等. 剪切应力作用下位错运动的晶体相场模拟[J]. 广西科学, 2015, 22(4): 400-406. HUANG S Y, LIU X H, XIE S, et al. Phase-field-crystal simulation of dislocation gliding under shear strain[J]. Guangxi Sciences, 2015, 22(4): 400-406. DOI:10.3969/j.issn.1005-9164.2015.04.008 |
| [21] |
杨涛, 陈铮, 董卫平. 应力诱发双位错组亚晶界湮没的晶体相场模拟[J]. 金属学报, 2011, 47(10): 1301-1306. YANG T, CHEN Z, DONG W P. Phase field crystal simulation of stress-induced annihilation of sub-grain boundary with double-array dislocation[J]. Acta Metallurgiga Sinica, 2011, 47(10): 1301-1306. |
| [22] |
TAKAKI T, TOMITA Y. Static recrystallization simulations starting from predicted deformation microstructure by coupling multi-phase-field method and finite element method based on crystal plasticity[J]. International Journal of Mechanical Sciences, 2010, 52(2): 320-328. DOI:10.1016/j.ijmecsci.2009.09.037 |
| [23] |
WU K A, VOORHEES P W. Phase field crystal simulations of nanocrystalline grain growth in two dimensions[J]. Acta Materialia, 2012, 60(1): 407-419. DOI:10.1016/j.actamat.2011.09.035 |
 2018, Vol. 34
2018, Vol. 34 


