【研究意义】渤海是一个近封闭的内海,地处北纬37°07′~41°00′,东经117°35′~122°15′的区域。渤海最北侧的辽东湾区域在冬季被冰雪覆盖,这直接威胁着辽东湾海域海洋平台的安全。为防止海冰对该海域平台的生产造成影响,在冬季必须对辽东湾的海冰情况进行监测。全天候海冰气象监测系统是一套集成度很高的海冰监测系统,于2014年12月12日在JZ9-3海域首次投入使用。作为一次革命性的创新,如何保障设备能够正常运行是必须考虑的问题,因此,在对系统的可靠性进行充分分析的基础上,提出提高设备可靠性的建议是必不可少的。【前人研究进展】故障树分析法是提高系统可靠性的一种风险分析方法,1961年美国的Watson[1]采用图形演绎、逻辑推理的方法,首次开发出了故障树分析法。在此基础上针对不同的情况,分别出现了动态故障树和模糊故障树的理论。1975年,Esary等[2]结合Markov理论和组合数学方法建立动态故障树理论,首次将故障树应用到动态分析中;1983年,Tanaka等[3]在传统可靠性理论的基础上,运用模糊数学原理来确定底事件的模糊重要度建立了模糊故障树理论。由于出发点不同,两种理论虽然有在同一系统中同时应用的需求,但实际操作中很难做到。【本研究切入点】本研究打破了动态故障树和模糊故障树两个概念中已经成熟的公式和计算方式,从故障树的定义出发,系统地将两种方法结合,获得动态模糊故障树各个参数的计算方法。【拟解决的关键问题】通过将动态模糊故障树理论应用于全天候海冰气象监测系统的可靠性研究,有效控制系统的薄弱环节,提高了系统的可靠性。
1 材料与方法 1.1 动态模糊故障树 1.1.1 动态故障树故障树分析法[4]以图形为基础,由基本的逻辑门符号、事件符号按照一定的逻辑关系组合而成,用于描述系统中各种事件之间的因果关系。动态故障树是在故障树分析理论中引入动态逻辑门,使系统具有冷、热备份和顺序相关等特性[5]。动态故障树除了具有故障树原本具有的与门、或门、异或门等,还具有动态与门、冷备件门等动态逻辑门。现在许多系统都存在一定的时序相关性,为更好地处理这个问题,需在传统故障树中引入动态逻辑门。
1.1.2 动态故障树的局限性动态故障树可以通过演绎的方式,对系统故障的发生过程及系统的可靠性进行全面的分析,即系统固定,底事件的发生概率固定,就能求解出顶事件的发生概率。然而,在实际的工程中,很多准确的数据是很难或者无法得到的,这就给动态故障树的应用造成了一定的困难。
1.1.3 动态模糊故障树为解决动态故障树所存在的不足,本文选择了在动态故障树的基础上引入模糊数学。模糊数学能够有效地处理研究对象的不确定性,即模糊性,借助模糊数学理论,可有效地弥补数据不足对动态故障树分析所造成的影响[6]。动态模糊故障树分析法是一种以动态故障树为基础,以模糊数学为手段对系统进行定性定量分析的方法。该方法与传统动态故障树相比,能够解决动态故障树无法解决实际工程的模糊性问题。
动态模糊故障树的分析步骤一般如下:①根据逻辑结构,绘制动态故障树;②查阅数据,找出能够确认故障率或概率密度函数的底事件;③对无法确认故障率或概率密度函数的单元进行分类,确定概率密度函数的表达式;④借助模糊数学,确定一段时间内底事件的发生概率;⑤通过概率密度函数类型和发生概率确定概率密度函数中相关参数;⑥计算顶事件的发生概率。
1.2 全天候海冰气象监测系统整套设备包括系统采集计算机、集成系统采集器、视频摄像头、气象仪、冰激振动探头、倾斜度探头和声发射探头。具体结构如图 1所示。
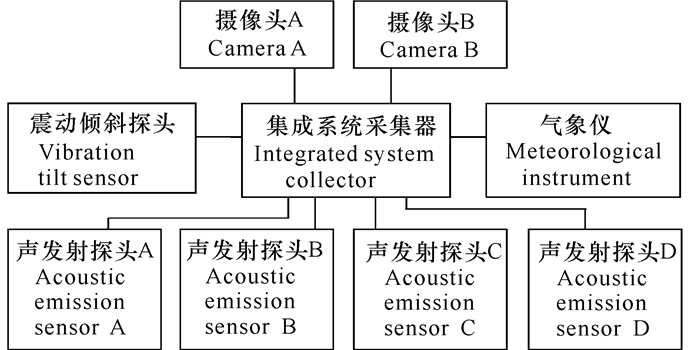
|
图 1 全天候海冰气象监测系统结构图 Fig.1 Structure chart of all-weather sea ice meteorological monitoring system |
与传统的海冰监测系统相比,该系统可通过声学信息对海冰撞击进行分析,具有整体检测、自动报警、自动分析、持续记录、损伤定位、远程传输等特点。同时系统可以适应低温、潮湿等恶劣环境,能够很好地完成海冰自动化监测的功能。在运行的几年里,通过利用系统监测数据,成功获得了海冰撞击与潮水、风速、船舶运动等因素之间的关系,为渤海海域海洋平台的冬季生产工作提供了有效保障。
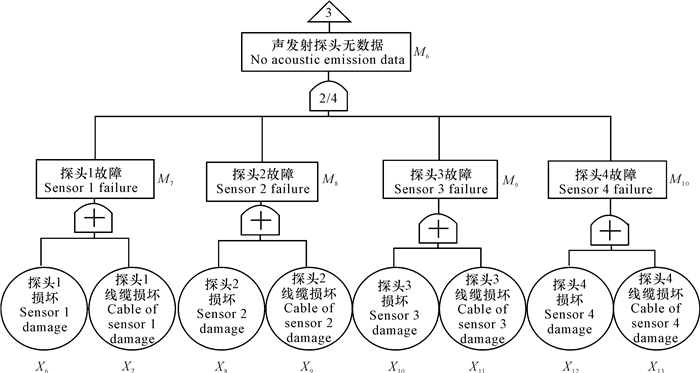
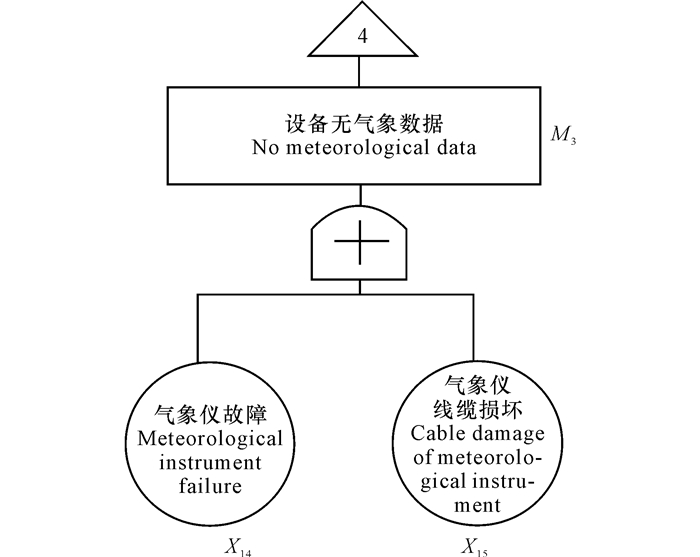
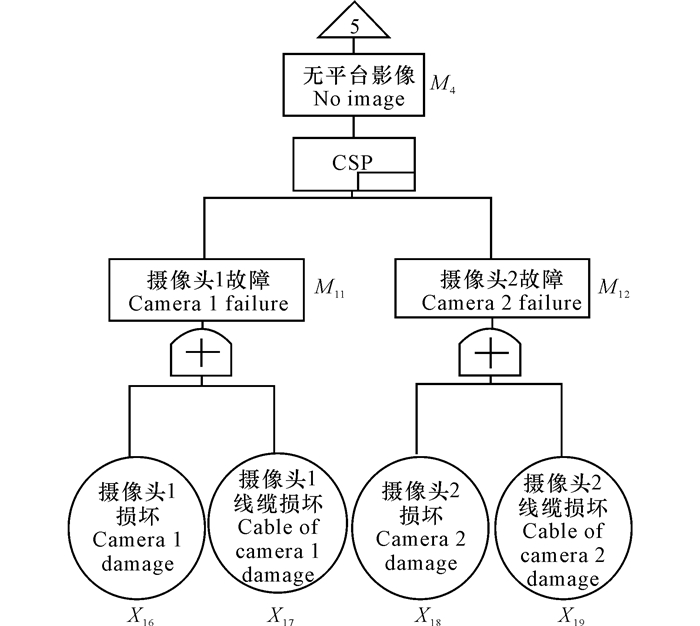
2 结果与分析 2.1 全天候海冰气象监测系统可靠性分析 2.1.1 故障树编制通过上文分析,全天候海冰气象监测系统是由集成系统采集器、2个视频摄像头、气象仪、冰激振动倾斜度探头和4个声发射探头这几个部分组成的。其中,2个摄像头一个运行,一个备用,当第一个摄像头故障时,系统会直接切换到第二个摄像头以保证系统的正常运转;冰激振动倾斜度探头和声发射探头只要其中之一工作就可保证系统的正常工作;4个声发射探头只要保证其中有3个可用,即损坏数量小于2即可得到需要的数据。由于树图的底事件有19个,故在建树的前期对系统进行不交化处理,处理的结果见图 2~7。
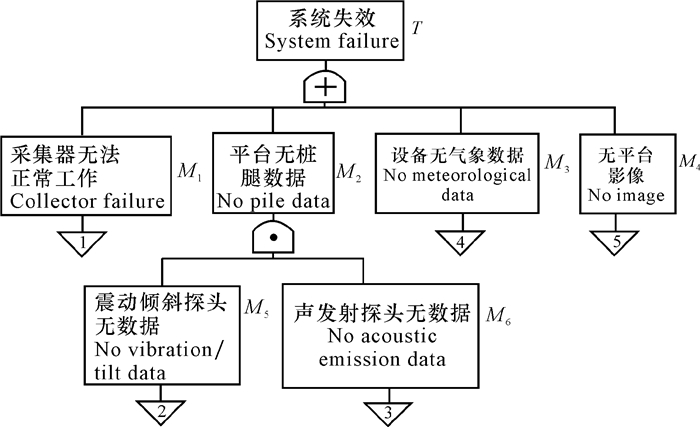
|
图 2 全天候海冰气象监测系统失效故障树 Fig.2 Fault tree of all-weather sea ice meteorological monitoring system |
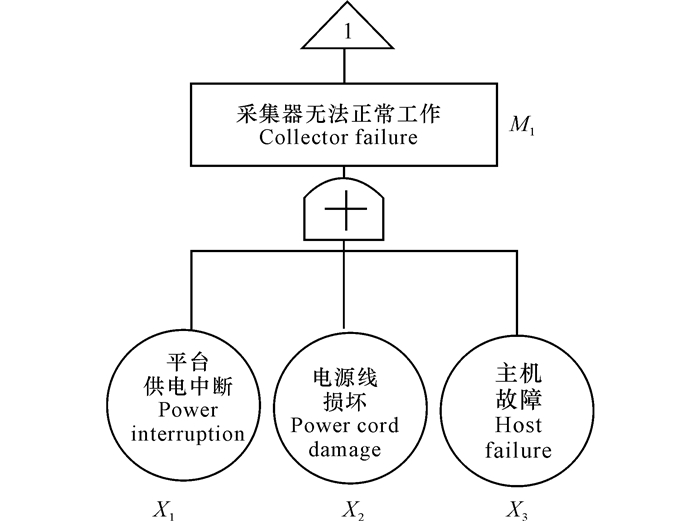
|
图 3 采集器失效故障树 Fig.3 Fault tree of collector |
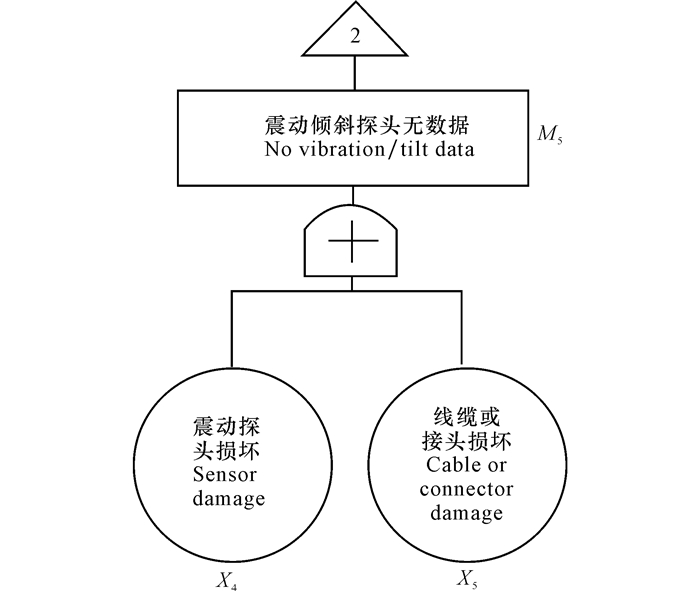
|
图 4 震动倾斜探头失效故障树 Fig.4 Fault tree of vibration tilt probe |
|
图 5 声发射探头失效故障树 Fig.5 Fault tree of acoustic emission probe |
|
图 6 气象仪失效故障树 Fig.6 Fault tree of meteorological instrument |
|
图 7 摄像头失效故障树 Fig.7 Fault tree of camera |
故障树的定性分析主要是对故障树顶事件的求解。动态故障树中引入了动态门。故系统失效不仅与底事件的组合有关,而且与底事件的发生顺序有关。为体现动态故障树的动态特性,将最小割集的概念延伸为最小顺序割集,即导致系统失效发生的最小失效事件序列。
动态门的动态约束性质分为逻辑约束和时间约束。逻辑约束是动态门的输入事件之间的与、或关系,时间约束是动态门的输入事件所需的失效顺序。基于这个原理,可以运用如下的动态故障树的最小割集算法[7]:
(1) 按照逻辑约束用相应的与门、或门代替动态门:用与门代替优先与门、冷备件门、温备件门、热备件门、顺序相关门,用或门和与门的嵌套代替功能相关门;
(2) 生成新的静态故障树的最小割集;
(3) 按照时间约束把最小割集延伸为最小顺序割集。
通过对各个故障树进行计算,分别得到各部分的最小顺序割集见表 1。
| 表 1 最小顺序割集 Table 1 The minimal cut sequence |
由各树的最小顺序割集可知,除摄像头故障树外,其他各树中不存在动态逻辑门,故可按照一般故障树进行计算,只需要计算故障率即可;摄像头故障树则需要单元的概率密度函数进行分析。根据设备厂商提供的资料,可以得到部分构件在冰期的故障率或概率密度函数(冰期以3个月计算),详见表 2。
| 表 2 部分构件的故障率或概率密度函数 Table 2 Failure rate/fialure rate function of partial component |
无法获得的数据则引入模糊数学的理论进行分析[8],首先采用专家判断法获取专家的得分,风险发生概率的等级量化值见表 3。
| 表 3 风险发生概率等级 Table 3 Probability ranking of risk occurrence |
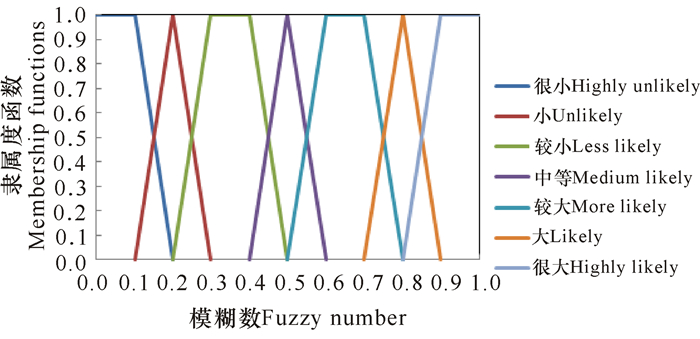
通常在描述事件的发生概率时,专家习惯用自然语言来表达评估意见,这些语言具有模糊性与不确定性,这时“较大”“较小”可以用模糊数来代替。如图 8所示,模糊数可以代替自然语言来表征事件发生概率。
|
图 8 代表自然语言的模糊数图 Fig.8 Fuzzy number map representing-natural language |
(1) 专家判断设备失效基本事件
在设备设计、施工、维修和管理等领域中,选择10位专家组成专家评估组,各个专家根据自身经验对各个基本事件发生的可能性大小做出判断,在认为可能的情况一栏中打勾,评估意见表 4所示。
| 表 4 专家评估意见表(举例) Table 4 Expert evaluation table(example) |
针对故障树中X1这一基本事件进行举例说明,专家判断结果为“小”0票,“较小”3票,“中等”1票,“较大”2票,“大”4票。
(2) 计算模糊数
这里认为10位专家意见的权重相等,自然语言通常具有模糊性,对其进行量化处理,采用模糊集合的λ截集。根据代替自然语言的模糊数图,隶属函数表达式为
| $ {f_L} = \left\{ \begin{array}{l} \frac{{x - 0.1}}{{0.1}}\left( {0.1 < x \le 0.2} \right)\\ \frac{{0.3 - x}}{{0.1}}\left( {0.2 < x \le 0.3} \right)\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right., $ | (1) |
| $ {f_{FL}} = \left\{ \begin{array}{l} \frac{{x - 0.2}}{{0.1}}\left( {0.2 < x \le 0.3} \right)\\ 1\;\;\;\left( {0.3 < x \le 0.4} \right)\\ \frac{{0.5 - x}}{{0.1}}\left( {0.4 < x \le 0.5} \right)\\ 0\;\;\;\;\;\;\;\;\;其他 \end{array} \right., $ | (2) |
| $ {f_M} = \left\{ \begin{array}{l} \frac{{x - 0.4}}{{0.1}}\left( {0.4 < x \le 0.5} \right)\\ \frac{{0.6 - x}}{{0.1}}\left( {0.5 < x \le 0.6} \right)\\ 0\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right., $ | (3) |
| $ {f_{FH}} = \left\{ \begin{array}{l} \frac{{x - 0.5}}{{0.1}}\left( {0.7 < x \le 0.8} \right)\\ 1\;\;\left( {0.6 < x \le 0.7} \right)\\ \frac{{0.8 - x}}{{0.1}}\left( {0.7 < x \le 0.6} \right)\\ 0\;\;\;\;\;\;\;其他 \end{array} \right., $ | (4) |
| $ {f_H} = \left\{ \begin{array}{l} \frac{{x - 0.7}}{{0.1}}\left( {0.7 < x \le 0.8} \right)\\ \frac{{0.9 - x}}{{0.1}}\left( {0.8 < x \le 0.9} \right)\\ 0\;\;\;\;\;\;\;其他 \end{array} \right.。$ | (5) |
设上述公式中,隶属函数的λ截集的上下限分别为
小(L):Lλ=[l1, l2],令λ=(x=0.1)/0.1,则l1=0.1λ+0.1,l2=0.3-0.1λ;
较小(FL):FLλ=[f1,f2], f1=0.1λ+0.2,f2=0.5-0.1λ;
中等(M):Mλ=[m1, m2],m1=0.1λ+0.4,m2=0.6-0.1λ;
较大(FH):FHλ=[h1,h2],h1=0.1λ+0.5, h2=0.8-0.1λ;
大(H):Hλ=[g1,g2],g1=0.1λ+0.7, g2= 0.9-0.1λ。
总的模糊集z为
| $ \begin{array}{l} {f_{FL \oplus H \oplus H \oplus FH \oplus H \oplus FH \oplus H \oplus M \oplus FL \oplus FL}} = \;\;{\rm{max}}\;\;|\\ {f_{FL}}\left( x \right) \wedge {f_H}\left( x \right) \wedge {f_H}\left( x \right) \wedge {f_{FH}}\left( x \right) \wedge {f_H}\left( x \right) \wedge \\ {f_{FH}}\left( x \right) \wedge {f_H}\left( x \right) \wedge {f_M}\left( x \right) \wedge {f_{FL}}\left( x \right) \wedge {f_{FL}}\left( x \right)| = \\ [3 \otimes \left( {0.1\lambda + 0.2} \right) + \left( {0.1\lambda + 0.7} \right) + 2 \otimes (0.1\lambda + \\ 0.4) + 4 \otimes \left( {0.1\lambda + 0.5} \right), 3 \otimes \left( {0.1\lambda + 0.2} \right) + \\ \left( {0.1\lambda + 0.7} \right) + 2 \otimes \left( {0.1\lambda + 0.4} \right) + 4 \otimes (0.1\lambda + \\ 0.5) |= \left| {\left( {\lambda + 4.1} \right), \left( {6.8 - \lambda } \right)} \right|。\end{array} $ | (6) |
平均模糊数为
| $ \begin{array}{l} \;\;\;\;W = \frac{1}{{10}}\left| {\left( {\lambda + 4.1} \right), \left( {6.8 - \lambda } \right)} \right| = |(0.1\lambda + \\ 0.41), \left( {0.68 - 0.1\lambda } \right)|。\end{array} $ | (7) |
令Wa=|(z1, z2)|=|(0.1λ+0.41), (0.68-0.1λ)|。则有:
| ${f_W}\left( z \right) = \left\{ \begin{array}{l} \frac{{z - 0.41}}{{0.1}}\ \ \ \left( {0.41 < z \le 0.51} \right)\\ 1\;\;\;\left( {0.51 < z \le 0.58} \right)\\ \frac{{0.68 - z}}{{0.1}}\ \ \ \left( {0.58 < z \le 0.68} \right)\\ 0\;\;\;\;\;\;\;\;\;其他 \end{array} \right.。$ | (8) |
(3) 将模糊数转化为模糊失效概率
通过左右模糊排序法进行计算,最大和最小模糊集分别为
| $ \begin{array}{l} {f_{{\rm{max}}}}\left( x \right) = \left\{ \begin{array}{l} x\left( {0 < x < 1} \right){\rm{ }}\\ 1\;\;\;\;\;其他 \end{array} \right., \\ {f_{{\rm{min}}}}\left( x \right) = \left\{ \begin{array}{l} 1 - x\left( {0 < x < 1} \right){\rm{ }}\\ 1\;\;\;\;\;\;其他 \end{array} \right., \end{array} $ | (9) |
则模糊数的左模糊可能性值和右模糊可能性值分别为
| $ \begin{array}{l} FP{S_R}\left( w \right) = {\rm{sup}}[{f_W}\left( x \right) \wedge {f_{{\rm{max}}}}\left( x \right)], {\rm{ }}\\ FP{S_L}\left( w \right) = {\rm{sup}}[{f_W}\left( x \right) \wedge {f_{{\rm{min}}}}\left( x \right)]。\end{array} $ | (10) |
W的模糊可能性值为
| $ FPS\left( w \right) = \frac{{|FP{S_R}\left( w \right) + 1 - FP{S_L}\left( w \right)|}}{2}, $ |
可得FPS(w)=0.595 4。
模糊失效率为
| $ \begin{array}{l} \;\;\;\;\;\;\;FFR = \left\{ \begin{array}{l} \frac{1}{{{{10}^k}}}\left( {FPS \ne 0} \right)\\ 0\left( {FPS = 0} \right) \end{array} \right.(k = 2.301 \times \\ {\left( {\frac{{1 - FPS}}{{FPS}}} \right)^{\frac{1}{3}}}). \end{array} $ | (11) |
故X1的发生概率为FFR=0.009 488=9.488×10-3。
将此方法应用于整个系统中,可以得到所有基本事件的发生概率(表 5)。
| 表 5 部分构件的模糊故障率 Table 5 Fuzzy failure rate of partial components |
通过以上数据可以求的除摄像头以外所有故障树的故障率,分别为P(M1)=2.159 8×10-2,P(M3)=2.576 8×10-2,P(M5)=2.246 8×10-2,P(M6)=0.395 9×10-2。
然而,摄像头故障之间存在顺序关系,不能只利用故障率进行计算,必须得出部件故障的概率密度函数,通过与有经验的工程师及工人进行沟通,得出一般情况下服从指数分布的结论,即其概率密度函数可以写成:
| $ f\left( t \right) = \lambda \;{e^{ - \lambda \;t}}, $ | (12) |
即故障率可以写成:
| $ F\left( t \right) = \int_0^t {\lambda \;{e^{ - \lambda \;t}}{\rm{d}}t = 1 - {e^{ - \lambda \;t}}} 。$ | (13) |
将表 5中得到的模糊故障率带入式2),得:λ17=3.787×10-3,λ19=3.787×10-3。通过冷备件门的相关知识可算出摄像头的故障率为P(M4)=0.021 49×10-2。
故设备的故障率为P(T)=4.762×10-2。
2.2 系统可靠性提升措施的研究 2.2.1 基本事件的概率重要度为达到降低设备故障风险的目的,最根本的方法就是降低基本事件的发生概率。由于各个基本事件对系统的影响差别很大,所以找出系统中对设备影响最大的基本事件进行防范是最易于实现、节约成本的方法。概率重要度是评价顶事件和基本事件概率变化相关性的一个评价参数,简单来说,在一个故障树中,基本事件的概率重要度越高,则对其进行控制的必要性就越高。概率重要度Ig(i)的表达式:
| $ {l_g}\left( i \right) = \frac{{\partial P\left( T \right)}}{{\partial {q_i}}}。$ | (14) |
以X1为例,由于故障树早期进行了不交化,所以与其不相关的子树可以当作常数来进行处理,将公式中的除X1以外的单元按常数处理,最终代入得到顶事件的发生概率与X1之间概率存在以下关系:
| $ P\left( T \right) = 0.962 \times {q_1} + 0.0385。$ | (15) |
将式15)代入式14),得Ig(1)=0.962。
用同样的方法对所有基本事件进行计算,可得所有基本事件的概率重要度如表 6所示。
| 表 6 所有构件的模糊故障率 Table 6 Fuzzy failure rate of all components |
根据结果可知,基本事件X1(平台供电中断)、X2(电源线损坏)、X3(主机故障)、X14(气象仪故障)、X15(气象仪线缆损坏)的概率重要度较高(大于0.9),应当重点进行防范。
2.2.2 措施的提出针对2.2.1提出的5个基本事件,分别进行研究。基本事件X1(平台供电中断)的控制方法是采用平台UPS电源,这样从根本上解决了平台供电可能出现的不稳定问题。而针对基本事件X2(电源线损坏)、X14(气象仪故障)、X15(气象仪线缆损坏),由于设备体积小、易更换,可以在设备运行期间准备一套新的备件,出现问题随时进行更换。而基本事件X3(主机故障),由于设备庞大、内部构造复杂,故暂时不做考虑。
2.2.3 措施效果验证根据采取的措施,对故障树进行相关修正,由于所改变的单元只有子树1和子树4,故只对这两个子树进行修改。修改后的子树见图 9和图 10。
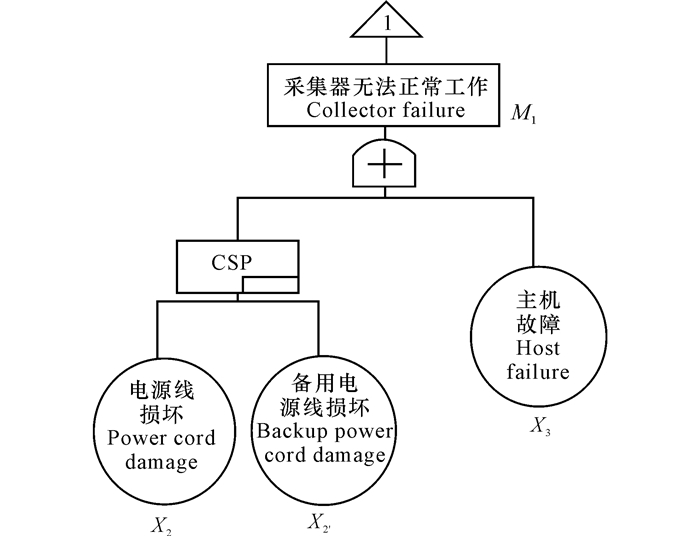
|
图 9 采集器失效故障树 Fig.9 Fault tree of collector |
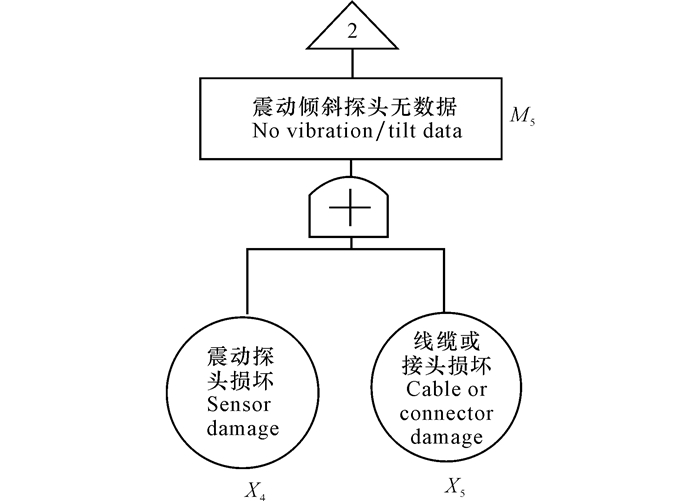
|
图 10 震动倾斜探头失效故障树 Fig.10 Fault tree of vibration tilt probe |
通过相同的计算方法对系统的可靠性进行计算,最终算得设备的故障率为P(T)=0.530×10-2。
截止至今,设备已经运行4年,并未出现影响设备运行的情况,和上文计算的故障率(0.530×10-2)相符。运行期间,设备出现了一次声发射探头松动,和分析结果相同,并未对系统的运行造成影响。
3 结论本文对全天候海冰气象监测系统的可靠性进行了研究,在动态故障树理论中引入了模糊数学的相关概念,提出了动态模糊故障理论。主要取得了如下成果:
① 在不采取任何措施的情况下,全天候海冰气象监测系统在一个海冰季的故障概率为4.762×10-2,约为5%。
② 运用动态模糊故障树对系统的可靠度进行提升后,全天候海冰气象监测系统在一个海冰季的故障概率为0.530×10-2,低于1%。
③ 由于重要事件主机故障难以用更换等简单方法进行保障,因此需要平台值班人员学习主机相关的理论知识,争取能够自行解决简单的故障。
④ 动态模糊故障树不能百分之百的反映设备的真实情况,只能够给出一个初步的措施。该措施应该随着对设备了解的不断累计逐步完善,尽量减少模糊单元的比例,最终得出更为准确的措施。
| [1] |
WATSON H.Launch control safety study[R]. Murray Hill, USA: Bell Telephone Laboratories, 1961.
|
| [2] |
ESARY J D, ZIEHMS H.Reliability analysis of phased missions[R]. Monterey, USA: Naval Postgraduate School Monterey, 1975: 213-236. http://www.ams.org/mathscinet-getitem?mr=446469
|
| [3] |
TANAKA H, FAN L T, LAI F S, et al. Fault-tree analysis by fuzzy probability[J]. IEEE Transaction on Reliability, 1983, 32(5): 453-457. |
| [4] |
詹锋. 一种面向业务的信息安全风险评估方法[J]. 广西科学院学报, 2006, 22(4): 364-366. ZHAN F. A risk assessment method for the security of appliedsystems[J]. Journal of Guangxi Academy of Sciences, 2006, 22(4): 364-366. |
| [5] |
SINGER D. Fault tree analysis based on fuzzy logic[J]. Computers&Chemical Engineering, 1990, 14(3): 259-266. |
| [6] |
PULLUM L L, DUGAN J B.Fault tree models for the analysis of complex computer-based systems[C]. Las Vegas, USA: Proceedings Annual Reliability and Maintainability Symosium, 1996. http://www.researchgate.net/publication/3628825_Fault_tree_models_for_the_analysis_of_complex_computer-based_systems?_sg=xmfVzCkElCxyFWzmh4Ywhzq-fHPetJA2Db0rvnn6nHVbpTIPZgzDHkAPUICqOIUOYN6vqwMMNmVYtWxhoms5dA
|
| [7] |
TANG Z H, DUGAN J B.Minimal cut set /sequence generation for dynamic fault trees[C]. Las Vegas, USA: Proccedings of Annual Reliability and Maintainability Symposium, 2004. http://www.researchgate.net/publication/4067922_Minimal_cut_setsequence_generation_for_dynamic_fault_trees
|
| [8] |
乐丛欢, 丁红岩, 董国海, 等. 基于模糊故障树的海洋立管破坏失效风险分析[J]. 自然灾害学报, 2012, 21(2): 173-179. LE C H, DING H Y, DONG G H, et al. Risk analysis of failure damage to marine riser based on fuzzy fault tree[J]. Journal of Natural Disasters, 2012, 21(2): 173-179. |
 2018, Vol. 34
2018, Vol. 34 


