2. 新疆财经大学新疆社会经济统计研究中心,新疆乌鲁木齐 830012;
3. 新疆维吾尔族自治区气象局人工影响天气办公室,新疆乌鲁木齐 830002
2. Research Center of Xinjiang Social and Economic Statistics of Xinjiang University of Finance and Economics, Urumqi, Xinjiang, 830012, China;
3. Xinjiang Weather Modification Office, Urumqi, Xinjiang, 830002, China
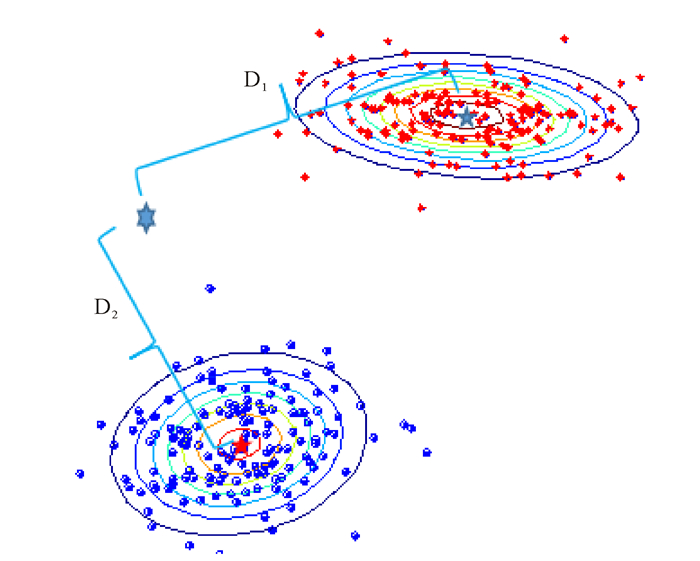
【研究意义】冰雹是由强对流天气系统造成的,它的产生会造成严重的经济损失,给农业、旅游业等产业带来不可估量的损失。新疆虽地处内陆干旱、沙漠地区,但仍是冰雹多发区,深受冰雹灾害的困扰。冰雹虽然来时快、持续时间短,但会造成持续性、毁灭性的灾害。因此,研究如何有效地防雹减灾来降低经济损失具有重要意义。【前人研究进展】国外自20世纪中期已开始冰雹的预测研究。Johnson等[1]针对强对流天气的回波识别阈值研究已取得很大进展,并且该方法在美国的实地测验过程中也取得较好的结果;Cotton等[2]利用冰晶的浓度进行预报;Jr Auer等[3], Smyth等[4], Witt等[5]结合回波反射率和云顶温度进行冰雹识别。国内虽然在这方面起步较晚,但近些年也有很大进展:夏文梅等[6]研究V型缺口在C波段多普勒雷达中的关系,路志英等[7]将暴雨冰雹的强度特征和纹理特征与探空数据(0℃和-20℃温度层高度)结合,利用粗糙集理论进行数据挖掘并建立识别模型。冰雹暴雨等强对流天气的回波图像具有云层图像的客观规律,利用这些规律也可得到判别雹云的数据[8-9]。【本研究切入点】目前,利用K-means聚类和CNN边缘检测对独立云层单体图像进行处理,可得到云层的轮廓方差特征,利用该特征可区别雹云与非雹云[10-11]。但将云层图像的内外轮廓距离差与云高数据相结合,有可能得到更准确的预测,所以本研究将两者相结合来分析雹云与非雹云。【拟解决的关键问题】利用云层图像内外轮廓距离差的方差及云层云高的一阶统计测度,构造距离判别函数对雹云与非雹云进行判别。距离判别的雹云识别原理如图 1所示。
|
图 1 距离判别的雹云识别解释图 Fig.1 Interpretation map of hail cloud recognition based on distance identification |
在计算雹云内外轮廓距离差前,要进行K-means聚类,以各像素间的相似度距离作为不同颜色间的差距。为让聚类结果更加准确,一般需要将图像像素值从RGB模型转到Lab模型。由于a、b层的像素矩阵Na、Nb已经包含所有像素信息,所以不需要将L层的信息表达出来。RGB模型转到Lab模型公式如下:
| $ \begin{array}{l} \;\;\;\;\;{N_a} = 1.474\;9\left( {0.221\;3R - 0.339\;0G + } \right.\\ \left. {0.117\;7B} \right) + 128, \end{array} $ | (1) |
| $ \begin{array}{l} \;\;\;\;\;{N_b} = 0.624\;5\left( {0.191\;4R - 0.605\;7G{\rm{ - }}} \right.\\ \left. {0.800\;6B} \right) + 128。\end{array} $ | (2) |
将K-means聚类后的图像采用canny算法进行边缘提取,将得到的边缘图像叠加得到一个二层轮廓的单体,计算内外轮廓的距离差,利用距离差计算内外轮廓的方差。内外层轮廓距离差算法步骤如下。
Step 1:将聚类分割单体得到的图像按公式(1)(2)的逆运算得到RGB值,按照下式将图像二值化处理。
| $ \begin{array}{l} {\rm{Gray = 0}}{\rm{.01}} * R + 0.59 * G + 0.3 * B, \\ g\left( {x, y} \right) = \left\{ \begin{array}{l} 0, \;\;\;\;\;\;\;{\rm{Gray > 127}}\\ 255, \;\;\;{\rm{Gray}} \le 127 \end{array} \right.。\end{array} $ | (3) |
Step 2:将得到的二值图像运用canny算法进行边缘检测,得到黄色区域轮廓、蓝色区域轮廓。将两个轮廓进行叠加,得到两层轮廓单体图像TZE。
Step 3:在TZE图像上以黄色轮廓的几何中心O为原点,建立直角坐标系,其中xi, yi表示像素值为1的横纵坐标。
| $ O = \\\left( {\frac{{\max \left\{ {{x_i}} \right\} - \min \left\{ {{x_j}} \right\}}}{2}, \frac{{\max \left\{ {{y_i}} \right\} - \min \left\{ {{y_j}} \right\}}}{2}} \right)。$ | (4) |
Step 4:从原点O射出一条射线,得到射线与两个轮廓的交点坐标(xYi, yYi)(xBi, yBi),绕原点每隔6°旋转画一射线,共得到60个交点,通过下式计算内外层轮廓距离差序列。
| $ \begin{array}{l} \;\;\;\;{d_i} = \sqrt {{{\left( {{x_{Bi}} - {x_{Yi}}} \right)}^2}{\rm{ + }}{{\left( {{y_{Bi}} - {y_{Yi}}} \right)}^2}} , i = 1, \\ 2, \cdots , 60。\end{array} $ | (5) |
Step 5:依据距离差序列计算方差,方差公式如下:
| $ {\sigma _i} = \frac{1}{{59}}\sum\limits_{j = 1}^{60} {\left( {{M_i}\left( j \right) - \overline M } \right)} , $ | (6) |
其中i表示图像序号,j表示射线的旋转次数。
根据以上步骤即可算出石河子地区雹云与非雹云图像内外轮廓差的距离方差。
2 雹云单体特征提取 2.1 云层图像云高数据的提取在强冰雹云中,云顶的温度可达-40℃以下,云低温度在0℃以上,云中有一条0℃等温线。所以各云层云滴结构也不同,顶部是冰晶和雪花,中部是过冷水滴和冰晶,底部是水滴。根据探空资料统计发现[12],一般0℃高度在4 km左右,-20℃层高度在7 km左右,所以根据云层的高度可反映雹云的部分特征。
以计算轮廓方差时提取的云层图像作为云高数据提取的原图。利用雷达软件,在一幅云层图像上不重复的选取k个值作为云层图像的云高数据(本研究设定k=20, 表 1)。
| 表 1 云高数据(节取,km) Table 1 Data of cloud height(section, km) |
为掌握数据的规律,有必要进一步讨论和分析得到的数据。
利用概率统计中的分布列,选取集中趋势中的算数平均值、离散趋势中的方差以及数据分布形状中的偏度和峰度这4个指标作为判断雹云与非雹云的统计测度。
均值:云高的均值。
| $ R = \sum\limits_{i = 1}^k {i \times {p_i}。} $ | (7) |
方差:用来度量云高与其均值之间的偏离程度。
| $ D = \sum\limits_{i = 1}^k {{{\left( {i - {\rm{mean}}} \right)}^2}} \times {p_i}。$ | (8) |
偏度:用于度量分布偏斜方向和程度的测度,是次数分配的非对称程度。
| $ \begin{array}{l} \;\;\;\;{\rm{skewness = }}\frac{1}{{{{\left( {{\rm{var}}\;{\rm{iance}}} \right)}^{\frac{3}{2}}}}} \cdot \sum\limits_{i = 1}^k {\left( {i - } \right.} \\ {\left. {{\rm{mean}}} \right)^3} \cdot {p_i}。\end{array} $ | (9) |
峰度:放映随机变量的分布形状量。
| $ \begin{array}{l} \;\;\;\;{\rm{kurtosis = }}\frac{1}{{{{\left( {{\rm{var}}\;{\rm{iance}}} \right)}^2}}} \cdot \sum\limits_{i = 1}^k {\left( {i - } \right.} \\ {\left. {{\rm{mean}}} \right)^4} \cdot {p_i}。\end{array} $ | (10) |
利用表 1中的数据可计算得到云高的均值、方差、偏度及峰度的一阶统计测度。
3 基于距离分析的雹云判别模型判别分析是多元统计分析中用于判别样本所属类型的一种方法,是将已知研究对象分成若干类型、且已得到各种类型样本的观测数据情况下,同时指定一种判别规则,建立判别式,对未知类型的样本进行判别分类。
3.1 距离判别法其基本思想是由训练样本得出每个分类的重心坐标,然后对待测样本求出它们离各个类别重心的距离远近,从而归入离得最近的类。最常用的距离是马氏距离,因为马氏距离可消除离散程度不一致所造成的影响。
本研究有两个已知总体G1(雹云)与G2(非雹云),一个待测样本X。判断测试样本X属于总体G1(雹云)还是总体G2(非雹云),主要看X到总体G1的重心x(1)近还是到总体G2的重心x(2)近。比较两者之间的距离D(X, G1)与D(X, G2),如果D(X, G1)D(X, G2),则X属于类G1;如果D(X, G1)>D(X, G2),则X属于类G2;如果D(X, G1)=D(X, G2),则样本X待判。
定义X到第i类重心x(i)的距离为马氏距离,即
| $ \begin{array}{l} \;\;\;\;{D^2}\left( {X, {G_i}} \right) = {\left( {X - {{\overline x }^{\left( i \right)}}} \right)^\prime }{\left( {\sum {_i} } \right)^{ - 1}}\left( {X - {{\overline x }^i}} \right)\left( {i = } \right.\\ \left. {1, 2} \right), \end{array} $ | (11) |
则判别准则可以写成如下形式:
| $ \begin{array}{l} W\left( X \right) = {D^2}\left( {X, {G_2}} \right) - {D^2}\left( {X, {G_1}} \right)\\ \left( \begin{array}{l} X \in {G_1}, {\rm{当}}W\left( X \right) > 0\\ X \in {G_2}, {\rm{当}}W\left( X \right) < 0\\ \;\;\;{\rm{待判, 当}}W\left( X \right) = 0 \end{array} \right.. \end{array} $ | (12) |
设有2个五维总体:G1(雹云),G2(非雹云),它们的样本估计均值分别为μ1和μ2,样本估计协方差矩阵分别为∑1和∑2(∑1, ∑2>0)。对任意给定的五维样本X=(x1, x2, x3, x4, x5),判定它来自哪个总体。按照距离最近的原则对X进行判别归类时,首先计算样本X到2个总体的马氏距离Di2(X), i=1, 2,然后再把X判别到距离最小的那个样本。如果
| $ D_l^2 = \mathop {\min }\limits_{i = 1, 2} \left\{ {D_i^2\left( X \right)} \right\}, $ | (13) |
则
距离判别的特点是直观、简单,它对变量的分布类型无严格要求,尤其是并不要求总体协方差阵相等。
3.2 模型构造本研究利用2009年至2011年3年的统计数据,新疆阿克苏市、阿瓦提县、拜城的降雹图像以及非降雹图像提取云高数据共18副图像作为训练样本,由第1节及2.2节计算步骤及方法可得到如表 2所示的雹云与非雹云图像特征值。利用此特征值对雹云与非雹云进行判别分析并构造判别模型,结果如表 3所示(所用软件为sas 9.2)。
| 表 2 石河子地区雹云与非雹云图像的特征值 Table 2 Eigenvalues of hail cloud and non hail cloud in Shihezi area |
| 表 3 线性判别函数 Table 3 Linear discriminant function |
由表 3中的判别函数的系数可以得到两组的判别函数分别是
| $ \begin{array}{l} \;\;\;\;{f_1} = - 348.202 + 135.890{x_1} - 83.774{x_2} - \\ 7.359{x_3} + 56.591{x_4} + 603.445{x_5}, \\ \;\;\;\;{f_2} = - 326.753 + 132.654{x_1} - 85.444{x_2} - \\ 8.006{x_3} + 60.605{x_4} + 489.303{x_5}。\end{array} $ |
其判别原则是:如果样本的f1(雹云)>f2(非雹云),则属于f1(雹云);如果f1(雹云)<f2(非雹云),则属于f2(非雹云)。
3.3 模型检验利用已知的分组数据对上述判别函数f1、f2进行检验,数据选取阿克苏地区2009年至2011年3年的另外4组统计数据作为待测样本(表 4),得到如表 5所示的分组结果。
| 表 4 待测样本一阶统计测度及距离方差 Table 4 First order statistical measure and distance variance of the sample to be measured |
| 表 5 分组结果 Table 5 Results of grouping |
从模型检验结果可知,测试样本集中共有4个样本,第1个和第4个被判成降雹,第2个及第3个被判为无雹,测试样本均正确归类。另从分组的出错估计可知该模型将降雹错判为非雹的概率是10%,将非雹错判为降雹的概率是12.5%,该模型的判别准确率为88.75%,准确率较高,表明此模型具有一定的判别效果。但模型存在一定的误判,将雹云判为非雹云;且因为样本容量小,所以判别函数在一定程度上受到限制。
4 结论基于距离判别法的雹云分类模型能有效地对雹云与非雹云进行分类;雹云与非雹云内外轮廓距离差的反差大小可反映降雹的可能性,云层高度信息也可作为是否降雹的一个依据,将两者相结合可增大判别的精准率,减少因冰雹灾害产生的损失。由于本研究样本容量有限,所以判别样本库的建立是提高判别准确率的有效途径。
| [1] |
JOHNSON J T, MACKEEN P L, WITT ARTHUR, et al. The storm cell identification and tracking algorithm:An enhanced WSR-88D algorithm[J]. Weather and Forecasting, 1998, 13(2): 263-276. DOI:10.1175/1520-0434(1998)013<0263:TSCIAT>2.0.CO;2 |
| [2] |
COTTON W R, TRIPOLI G J, RAUBER R M, et al. Numerical simulation of the effects of varying ice crystal nucleation rates and aggregation processes on orographic snowfall[J]. Journal of Applied Meteorology, 1986, 25(11): 1658-1680. DOI:10.1175/1520-0450(1986)025<1658:NSOTEO>2.0.CO;2 |
| [3] |
AUER A H JR. Hail recognition through the combined use of radar reflectivity and cloud-top temperatures[J]. Monthly Weather Review, 1994, 122(9): 2218-2221. DOI:10.1175/1520-0493(1994)122<2218:HRTTCU>2.0.CO;2 |
| [4] |
SMYTH T J, BLACKMAN T M, ILLINGWORTH A J. Observations of oblate hail using dual polarization radar and implications for hail-detection schemes[J]. Quarterly Journal of the Royal Meteorological Society, 1999, 125(555): 993-1016. DOI:10.1002/(ISSN)1477-870X |
| [5] |
WITT A, EILTS M D, STUMPF G J, et al. An enhanced hail detection algorithm for the WSR-88D[J]. Weather and Forecasting, 1998, 13(2): 286-303. DOI:10.1175/1520-0434(1998)013<0286:AEHDAF>2.0.CO;2 |
| [6] |
夏文梅, 王晓君, 孙康远, 等. V型缺口在C波段多普勒雷达中的应用研究[J]. 气象, 2016, 42(1): 67-73. XIA W M, WANG X J, SUN K Y, et al. Application study of 'V' notch used in C band doppler radar[J]. Meteorological Monthly, 2016, 42(1): 67-73. |
| [7] |
路志英, 刘海, 贾惠珍, 等. 基于雷达反射率图像特征的冰雹暴雨识别[J]. 物理学报, 2014, 63(18): 189201. LU Z Y, LIU H, JIA H Z, et al. Recognition of hail and rainstorm based on the radar reflectivity image features[J]. Journal of Physics, 2014, 63(18): 189201. DOI:10.7498/aps.63.189201 |
| [8] |
李少云, 王德良, 樊志超, 等. 郴州市冰雹天气预测预警及人工防雹方法研究[J]. 南方农业, 2014, 8(27): 156-158. LI S Y, WANG D L, FAN Z C, et al. Research on hail weather predict and forecast and artificial hail suppression method in Chenzhou city[J]. South China Agriculture, 2014, 8(27): 156-158. |
| [9] |
徐艳华. 冰雹的预测及其防治[J]. 气象水文海洋仪器, 2009, 26(3): 159-161. XU Y H. Hail prediction and prevention[J]. Meteorological, Hydrological and Marine Instruments, 2009, 26(3): 159-161. |
| [10] |
王雪, 李国东, 廖飞佳. 雹云图像的识别指标设计[J]. 哈尔滨理工大学学报, 2016, 21(1): 46-50. WANG X, LI G D, LIAO F J. Design the recognition index of hail cloud image[J]. Journal of Harbin University of Science and Technology, 2016, 21(1): 46-50. |
| [11] |
王雪, 李国东. 快速聚类和3阶CNN算法在雹云判别中的应用[J]. 湖南科技大学学报:自然科学版, 2016, 31(3): 123-128. WANG X, LI G D. Application of K-means clustering and CNN algorithm in hail cloud determination[J]. Journal of Hunan University of Science & Technology:Natural Science Edition, 2016, 31(3): 123-128. |
| [12] |
刘鹏, 蔡衡, 黄天福. 冰雹云识别和作业时机的选择[J]. 农业服务, 2011, 28(2): 255-256. LIU P, CAI H, HUANG T F. Identification of hail clouds and timing of operations[J]. Agricultural Services, 2011, 28(2): 255-256. |
 2018, Vol. 34
2018, Vol. 34 


