【研究意义】频繁序列是一种基本的序列模式,定义为相对于给定的最低频率阈值,频繁发生的事件或项目的有序列表,其中项目可以是DNA序列中的核苷酸。序列模式挖掘是数据挖掘中的一项重要任务,在模式挖掘中,频繁序列挖掘问题已被深入研究,是计算生物学、时间序列分析和文本挖掘的核心任务,应用领域广泛,包括分析时间戳购物数据,挖掘网络访问模式(WAP)[1],查找DNA序列中的相关基因[2],以及分类蛋白质[3]等。在实际中,序列模式挖掘被广泛地应用于各种序列数据集中,如生物信息学上的基因微阵列数据,从中挖掘哪些基因组合模式在某类病人中会频繁出现;以单词作为项目(item)的文档序列,研究在不同文档中单词序列的出现模式;用户点击流数据,用于挖掘用户的频繁点击模式,建立用户模型,完善网站功能与UI结构。除此之外,只要是序列数据集,都可以利用序列模式挖掘获得规律。【前人研究进展】目前序列挖掘的研究主要分为两类。一类将基于约束规划(CP)技术与模式挖掘相结合。2008年,De Raedt等[4]针对项集挖掘(CP4IM)提出CP的数据挖掘(DM)框架,提供了一个表述性的且灵活的表示模型。模式的新的约束通常需要在特定的方法中实现,但可以轻松地集成到该CP框架中,使数据挖掘问题受益于几种通用和高效的CP求解技术。2011年Guns等[5]提出在项集挖掘中使用的一些典型约束(例如频率,极大性,单调性)如何在CP中制定使用。这项研究是项集挖掘的第一个CP方法,显示出良好的表述性因素。2013年,Jabbour等[6]提出一种基于布尔可满足性问题(SAT)的编码,用于发现项目序列以及项集序列中的频繁、闭合和最大模式的问题。这种新的研究趋势为人工智能(AI)和数据挖掘之间的交叉渗透提供了很好的机会。另一类,对当前最常用且最有效的序列挖掘技术——模式增长(pattern growth)[7]方法进行改进。由于频繁序列挖掘器需要探索指数级的搜索空间,使得在大量长频繁序列模式存在的情况下,如在具有小字母表的DNA或蛋白质序列数据集中,或者在支持度阈值较低时、字母表较大的weblog数据集中,挖掘极具挑战性。因此有研究者提出基于二叉决策图(BDD)的数据挖掘方法:2009年,Loekito等[8]提出了一种称为SeqBDD的新的BDD类型,并成功将其应用于频繁子序列挖掘,展现出BDD的良好压缩性能。2010年,Cambazard[9]通过将所有项集的集合编译成BDD来解决频繁项集挖掘问题,然后通过查询BDD来提取频繁的项集。【本研究切入点】鉴于CP技术的表述性和灵活性,但存在搜索空间爆炸的问题;而二叉决策图(BDD)及其拓展结构具有高紧凑性和易操作性,一定程度上可以解决搜索空间爆炸问题,为处理大规模数据提供技术支撑。因此,提出基于SAT的频繁序列挖掘的符号OBDD算法,解决模式挖掘中输出尺寸巨大,很难快速从中检索相关信息等问题。【拟解决的关键问题】将频繁序列挖掘问题构建为SAT模型,通过对SAT的符号OBDD表示,并通过对SAT中约束进行OBDD操作给出了基于SAT的频繁模式挖掘的符号求解技术。最后通过实例证实算法的可行性以及准确性。
1 预备知识 1.1 布尔可满足性问题(SAT)布尔可满足性问题是一个判定经典命题逻辑公式是否一致的问题,是研究最多的多项式复杂程度的非确定性问题(NP-C问题)之一。
定义1.1.1 合取范式Φ(Conjunctive Normal Form,简称CNF):命题变元(p)及其否定(¬p)称为文字(literals);有穷个文字的析取构成子句(clause);有穷个子句的合取(conjunction)组成合取范式Φ。
合取范式Φ可以理解为一些布尔变量的或与表达式,表达式中只能使用与、或、非。使用线性Tseitin的编码[10]可以将任何命题公式转化为CNF。以下几种都是合取范式:
| $ \begin{array}{l} \neg A \wedge \left( {B \vee C} \right)\\ \left( {A \wedge B} \right) \wedge \left( {\neg B \vee C \vee \neg D} \right) \wedge \left( {D \vee \neg E} \right)\\ \left( {\neg A \vee B} \right)\\ A \wedge B \end{array} $ |
定义1.1.2 解释(interpretation)M:给定一个合取范式Φ以及Φ的一个赋值M,M为一个模型,当且仅当M(Φ)=true,称M满足合取范式Φ。
定义1.1.3 布尔可满足问题:给定一个布尔公式Φ(本文布尔公式以合取范式表示),若存在Φ的一个解释M,使得解释M满足布尔公式Φ,称布尔公式Φ是可满足的(satisfiable);如果在Φ的赋值空间内不存在这样的解释M,则称布尔公式Φ是不可满足的(unsatisfiable)。
1.2 SAT求解器目前大多数高效的SAT求解器都是基于DPLL算法[11](Davis-Putnam-Logemann-Loveland),它是一种完全的、基于回溯的算法。DPLL算法主要采用了深度优先搜索(Depth-first Search,DFS)算法思想。深度优先搜索算法指的是按照某种条件往前试探搜索,如果前进中遭到失败则回溯到上一层结点另选通路继续搜索,直到找到符合条件的目标为止。基本的DPLL算法包含3个主要步骤:
① 变量决策:在搜索树的每个层级上选择一个还未被赋值的决策变量并赋为一个布尔值。
② 赋值过程:推导并传播强制文字分配,简化子句,减少原始问题中的子句数。
③ 回溯过程:当搜索遇到冲突时,搜索过程从深的决策层返回到浅决策层。冲突子句(学习子句)通过自下而上遍历蕴涵图(implication graph)产生[12-13]。当产生的冲突子句仅包含一个来自当前决策层的文字时,学习或冲突分析过程停止。该冲突子句表明,当前层级的唯一文字(称为断言文字)隐含在上一层级(称为断言层),是该子句中其他文字的最大层级。求解器回溯到断言层并将断言文字分配为true。当生成空冲突子句时,原始公式记录为不可满足;当找到模型时,该公式为可满足的,记录模型。
1.3 频繁序列挖掘(FPS)定义1.3.1 项目序列(Sequences of items):给定项目的有限集合字母表Σ,通配符是不在Σ中的新符号,该符号可匹配字母表中的任一符号。Σ上的项目序列s由属于Σ的符号s0…sn-1表示。其长度表示为|s|,序列中符号的所有位置由集合Ps={0, …, |s|-1}表示。
定义1.3.2 模式(Pattern):Σ上的模式为序列x=x0…xm-1,其中x0∈Σ,xm-1∈Σ,xi∈Σ∪{*},i=1, …, m-2。
若∀i∈{0, …, m-1},xi=sl+i或xi=*,则称在序列s的位置l∈Ps处,x包含于序列s=s0…sn-1,记为x≼ls。如果对于∃l∈Ps使得x≼ls,则称x包含于s。x覆盖于s定义为集合Ls(x)={l∈Ps|x≼ls}。x在s中的支持度的值为|Ls(x)|。
定义1.3.3 频繁模式:给定序列s,模式x,最小支持度阈值λ≥1,若Ls(x)≥λ,则x是序列s中相对于支持度λ频繁的模式。一个项目序列中的频繁模式挖掘问题包含计算所有相对于λ频繁的模式集合Msλ。
例如,对于序列s=aaccbcabcba,模式x=a*c。由于x≼0s,x≼1s,x≼6s,得到Ls(x)={0,1, 6}, 这种情况下,若假定最小支持度阈值等于3,那么模式x是序列s的一个频繁模式。
1.4 二叉决策图(BDD)BDD[14]是一个规范的有向无环图(DAG)数据结构,用于紧凑地表示布尔公式。BDD也可以视为相同子树合并的二叉决策树。有序二叉决策图(OBDD)[15]是布尔函数的一种有效图形和数学描述技术。
定义1.4[16] 对于从{0,1}n到{0, 1}的布尔函数f(x1, x2, …, xn)和给定的变量序π,一个OBDD就是用于表示布尔函数f(x1, x2, …, xn)的一个有向无环图,它满足:
① OBDD中的结点分为非终结点和终结点两类。没有后继子结点或者没有输出弧的结点称为终结点,即终结点0和终结点1,分别表示布尔常量0和1;除终结点之外的结点称为非终结点;
② 每个非终结点u具有四元组属性(poin-ter(u), var(u), low(u), high(u)),其中,pointer(u)表示结点u所对应的布尔函数;var(u)表示结点u的标记变量;low(u)表示结点u所对应的函数中变量var(u)取值为0时对应的0-分支子结点;high(u)表示结点u所对应的函数中变量var(u)取值为1时对应的1-分支子结点;
③ 每个非终结点有且仅有两条输出弧,将它们和各自的两个分支子结点连接在一起。结点u和low(u)的连接弧称为0-边,结点u和high(u)的连接弧称为1-边;
④ 对于OBDD中的任意结点u,都有low(u)≠high(u);对于OBDD中的任意两个var(u)=var(v)的不同结点u和v,都有low(u)≠low(v),或者high(u)≠high(v),或者low(u)≠low(v)且high(u)≠high(v);
⑤ 在OBDD的任一有向路径上,布尔函数f(x1, x2, …, xn)中的每个变量均以变量序π所规定的次序依次最多出现一次。
定义1.4中所定义的OBDD实质上就是简化的OBDD,即ROBDD(Reduced OBDD)。
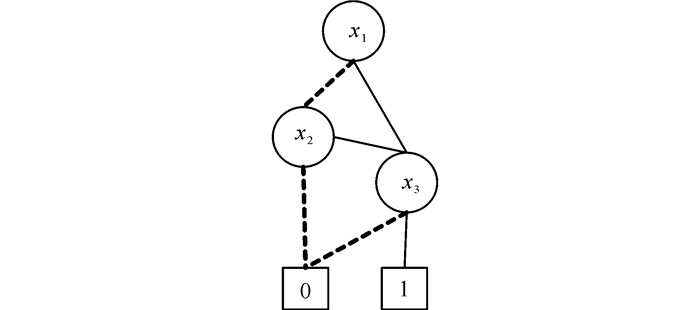
例如,对于布尔函数f=(x1+x2)·x3在变量序:x1<x2<x3下所对应的OBDD如图 1所示。在布尔函数的OBDD的表示中,对于变量的一组赋值,所得到的函数值由根结点到一个终结点的一条路径决定。这条路径所对应的分支由变量的这组赋值来决定,该分支的终结点所标识的值就是变量在这组赋值下所对应的函数值。
|
图 1 布尔函数f=(x1+x2)·x3的OBDD表示 Fig.1 OBDD for Boolean function f=(x1+x2)·x3 |
在OBDD中提供了以下2条简化规则。
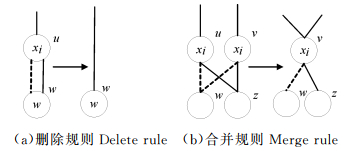
规则1(删除规则):对于OBDD中的结点u,如果low(u)=high(u),则删除结点u,并将结点u的所有入边指向low(u)结点;
规则2(合并规则):对于OBDD中的结点u和v,如果var(u)=var(v),low(u)=low(v)且high(u)=high(v),则删除其中一个结点,并将被删除结点的所有入边指向保留结点。该规则同样适用于具有相同标号的终结点。
OBDD中的删除规则和合并规则如图 2所示。
|
图 2 OBDD的简化规则 Fig.2 Simplified rules for OBDD |
基本思想在于使用命题变量来表示候选模式中元素的位置,以及使用基数约束[6]推导候选模式的支持度。
令Σ={e1, …, em}为字母表,s为Σ上的序列,长度为n,λ为最小支持度阈值。将s中出现的每个字符e关联到ke个命题变量的集合xe, 0, …, xe, (ke-1)使得ke=min(max(Ls(e))+1, n-λ+1),变量xe, i表示e在候选模式中,位置为i。xe, i=1表示候选模式中存在元素e,且位于模式的第i位,xe, i=0表示元素e不位于模式的第i位。{0, …, min(max(Ls(e)), n-λ)}对应于在候选模式中e的所有可能位置集合,因此只需将min(max(Ls(e))+1, n-λ+1)个变量关联到每个字符e,减少约束个数,以便加速求解。
约束1:第一个符号必须是一个固定的字符(不同于通配符)。该属性由以下简单子句表示:
约束2:由二进制子句组成的以下约束获取候选模式不存在的位置:
| $ \underset{e\in \mathit{\Sigma }, 0\le l\le n-1, 0\le i\le {{k}_{e}}-1}{\mathop{\vee }}\, \left( {{x}_{e, i}}\wedge {{s}_{l+i}}\ne e \right)\to {{y}_{l}}, $ |
其中y0, …, yn-1是n个新的命题变量。如果候选模式不在s中的位置l,则在上述公式中yl=1。在经典命题逻辑中,A→B:=¬A∨B,因此上述公式可以看作是二进制子句集(表达式sl+i≠e是常数,即sl+i≠e∈{0, 1})。
约束3:在枚举序列s中相对于支持度阈值λ的所有频繁模式问题中,需要表示候选模式至少出现λ次。该属性通过以下基数约束获得:
若该约束不满足,则意味着至少存在n-λ+1个位置候选模式不出现。可见,候选模式出现的位置最多存在λ-1个,即不是频繁的。否则至少存在λ个候选模式的位置,即该模式为频繁的。因此,该约束能够推导出所考虑候选模式的支持度,以判定它是否大于或等于最小支持度阈值。
在给定序列s中枚举所有频繁模式的问题由约束1、约束2和约束3表示。
例:考虑序列aabb的频繁模式挖掘问题,最小支持度阈值为2。编码对应于以下公式:
| $ {\rm{约束1}}:{x_{a, o}} \vee {x_{b, o}}, $ | (1) |
| $ {\rm{约束2}}:{x_{a, o}} \to \left( {{y_2} \wedge {y_3}} \right), $ | (2) |
| $ {x_{a, 1}} \to \left( {{y_1} \wedge {y_2} \wedge {y_3}} \right), $ | (3) |
| $ {x_{b, o}} \to \left( {{y_0} \wedge {y_1}} \right), $ | (4) |
| $ {x_{b, 1}} \to \left( {{y_0} \wedge {y_3}} \right), $ | (5) |
| $ {x_{b, 2}} \to \left( {{y_2} \wedge {y_3}} \right), $ | (6) |
| $ {\rm{约束3}}:{y_0} + {y_1} + {y_2} + {y_3} \le 2。$ | (7) |
对于所有的布尔解释M,若M(xa, i)=M(xb, i),则y0+y1+y2+y3=4。因此,M(xa, i)≠M(xb, i), 表示在同一位置不能有不同的实体字符。此外,由约束3可得对于所有布尔解释M,必须有M(xa, 1)=0。即元素a不出现于所有候选模式的第1位。用{xa, 0, xa, 1, xa, 2, xb, 0, xb, 1, xb, 2}的子集描述公式的每个布尔模型,可得模式为{{xa, o},{xb, o}和{xa, o,xb, 2}}。对应于模式a,b和a*b。
2.2 SAT的符号OBDD表示OBDD为布尔函数的表示形式,故在OBDD表示SAT之前,需先将SAT中的约束子句转化为布尔函数。
例如,对于上述例子中的约束,公式(2)~公式(6)可以分别表示为布尔函数x′a, o+y2·y3;x′a, 1+y1·y2·y3;x′b, o+y0·y1;x′b, 1+y0·y3;x′b, 2+y2·y3其中“·”“′”和“+”分别表示布尔“与”“非”和“或”运算。由此可得所有约束子句对应的OBDD表示,如图 3所示。

|
图 3 约束子句的符号OBDD表示 Fig.3 Symbolic OBDD representation of the constraint clauses |
运用深度优先结合OBDD算法挖掘频繁序列。算法步骤如下:
Step 1:根据给定的序列以及最小支持度阈值,列举所有约束子句,并分别转化为布尔函数。将约束1表示为OBDD。
Step 2:将SAT中约束2的变量根据该变量与其他变量之间约束关系的个数大小进行递增排序,然后将SAT中的约束按照此变量序进行归类,将每一类中的约束进行OBDD的“与”操作,最后对所有约束2以及约束1进行OBDD的“与”操作。
基于SAT的符号OBDD描述,求解SAT所有解的最直接方法就是利用OBDD的“与”操作,将SAT中的约束逐个的进行“与”运算,最后得到的OBDD即为SAT的所有解。但符号直接求解法在求解过程中,可能会使计算过程中生成的OBDD过于庞大,从而产生组合爆炸。而且基于OBDD的各种操作,其计算时间主要取决于参与操作的OBDD的大小。为改善算法的性能,先对SAT中的所有变量根据其在约束图中的度的大小进行递增排序,其中变量的度是指该变量与其他变量之间的约束关系的个数。假设按度的大小递增排序后的变量序为y1<y2<…<yn,然后将SAT中的约束按照此变量序进行归类,即所有包含变量y1的约束归为一类,然后在剩余的约束中将包含变量y2的约束也归为一类,依此类推。先将每一类中的约束进行OBDD的“与”操作,然后对所有约束进行OBDD的“与”操作。
Step 3:将约束3表示为OBDD,然后和约束1, 2“与”后的OBDD进行“与”操作,所得的OBDD即为满足所有约束的SAT的所有解,也即所给序列中相对于最小支持度阈值λ的所有频繁模式。图中的任意一条从根结点到终结点1的路径上取值为1的变量即为SAT的解,在路径中缺少的变量表示可以取0和1值。
3 实例分析基于DPLL的基本思路,结合符号OBDD算法,对FPS问题的SAT模型进行求解,同时为验证该算法的正确性和可行性,运用实例进行分析,对于上述例子(序列aabb的频繁模式挖掘问题),求解的主要步骤如下:
① 列举所有约束子句,并转化为布尔函数,约束1的OBDD如图 3a所示。
② 对SAT中约束2的所有变量根据该变量与其他变量之间的约束关系的个数大小进行递增排序,排序后的变量序为xa, o<xb, o<xa, 1<xb, 1<xb, 2<y0<y1<y2<y3。
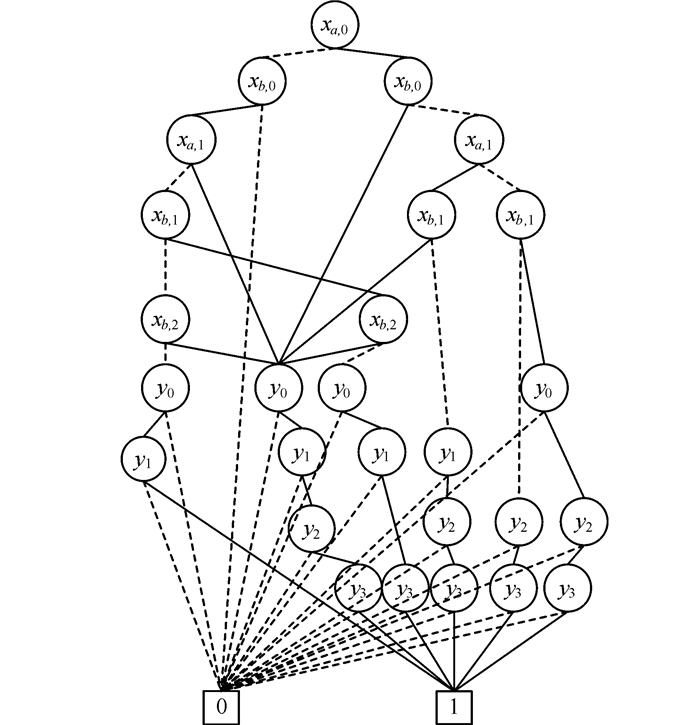
③ 将SAT中的约束按照此变量序进行归类:约束(4)xb, o→(y0∧y1)和约束(5)xb, 1→(y0∧y3)为一类;约束(3)xa, 1→(y1∧y2∧y3)为一类;约束(2)xa, o→(y2∧y3)和约束(6)xb, 2→(y2∧y3)归为一类,并按类进行OBDD的“与”操作,然后再“与”上约束1,由此可得约束1“与”约束2的OBDD表示,如图 4所示。
|
图 4 约束1“与”约束2的OBDD表示 Fig.4 OBDD representation of constraint 1 "and" constraint 2 |
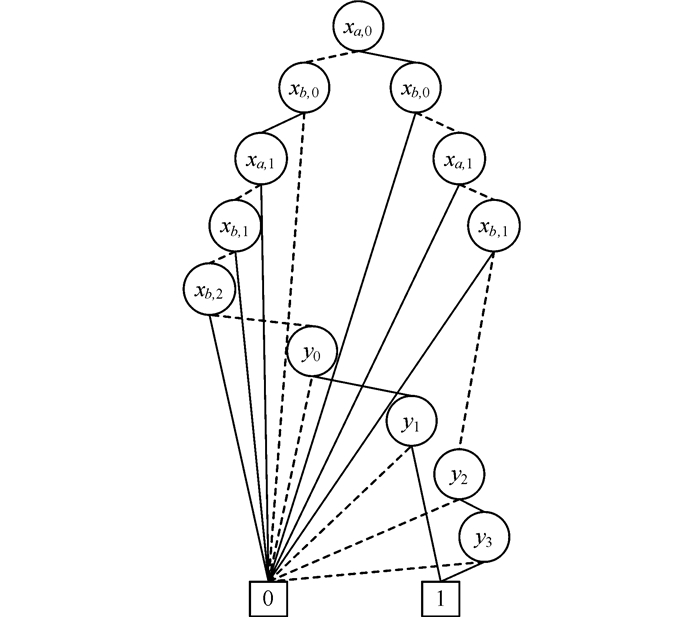
④ 将约束3表示为OBDD,如图 3g所示。对约束1、约束2、约束3进行OBDD“与”操作,可得SAT所有解的OBDD表示(图 5),即所给序列中相对于最小支持度阈值λ的所有频繁模式。图中从根结点到终结点1的路径x′a, oxb, ox′a, 1x′b, 1x′b, 2y0y1和xa, ox′b, ox′a, 1x′b, 1y2y3分别表示频繁模式{xb, o}和{{xa, o},{xa, o, xb, 2}}, 对应于模式b和a,a*b。
|
图 5 SAT所有解的OBDD表示 Fig.5 OBDD representation of all solutions of SAT |
本研究鉴于OBDD的高紧凑性和易操作性的特点,基于布尔可满足的思想与理论,以频繁序列挖掘问题为对象,探讨该问题的SAT模型以及相应的求解算法,减少了问题的空间需求,减缓了组合爆炸问题,得到了良好的研究结果。
数据挖掘是当前研究的主流方向。本研究只是在序列挖掘方面作了一些有益的探索工作,下一步研究方向和方法主要集中于两点:①将SAT模型以及BDD符号算法用于闭合、最大、最小频繁项集挖掘、关联规则挖掘等; ②由于符号OBDD算法的求解时间主要依赖于OBDD图的大小,因此如何减小参与操作的OBDD图的大小,进一步提高算法的执行效率,是值得探究的方向之一。
| [1] |
PEI J, HAN J, WANT W. Mining sequential patterns with constraints in large databases[C]. McLean Virginia: Proceedings of the 11th International Conference on Information and Knowledge Management (CIKM), 2002: 18-25. http://www.researchgate.net/publication/2563007_Mining_Sequential_Patterns_with_Constraints_in_Large_Databases
|
| [2] |
MA Q, WANG J, SASHA D, et al. DNA sequence classification via an expectation maximizationalgorithm and neural networks:A case study[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C:Applications and Reviews, 2001, 31(4): 468-475. DOI:10.1109/5326.983930 |
| [3] |
FERREIRA P G, AZEVEDO P J. Protein sequence classification through relevant sequences mining and bayes classifiers[C]//Portuguese Conference on Artificial Intelligence. [S.l.: s.n.], 2005: 236-247. http://www.springerlink.com/index/y8j0n7n2121j506h.pdf
|
| [4] |
DE RAEDT L, GUNS T, NIJSSEN S. Constraint programming for itemset mining[C]. New York, NY: KDD '08 Proceedings of the 14th ACM SIGKDD international conference on knowledge discovery and data mining, 2008: 204-212. http://dl.acm.org/citation.cfm?id=1401919
|
| [5] |
GUNS T, NIJSSEN S, DE RAEDT L. Itemset min- ing:A constraint programming perspective[J]. Artif Intell, 2011, 175: 1951-1983. DOI:10.1016/j.artint.2011.05.002 |
| [6] |
JABBOUR S, SAIS L, SALHI Y. Boolean satisfiability for sequence mining[C]. New York, NY: CIKM '13 Proceedings of the 22nd ACM International Conference on Information & Knowledge Management, 2013: 649-658. http://dl.acm.org/citation.cfm?id=2505577
|
| [7] |
PEI J, HAN J, MORTAZAVI-ASL B, et al. Mining sequential patterns by pattern-growth:The PrefixSpan approach[J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(11): 1424-1440. DOI:10.1109/TKDE.2004.77 |
| [8] |
LOEKITO E, BAILEY J, PEI J. A binary decision diagram based approach for mining frequent subsequences[J]. Knowledge & Information Systems, 2010, 24(2): 235-268. |
| [9] |
CAMBAZARD H, HADZIC T, O'SULLIVAN B. Knowledge compilation for itemset mining[C]//Conference on ECAI 2010: European Conference on Artificial Intelligence. [S.l.]: IOS Press, 2010: 1109-1110. http://dl.acm.org/citation.cfm?id=1861229
|
| [10] |
TSEITIN G. On the complexity of derivations in the propositional calculus[J]. Zap Nauchn Sem Lomi, 1968, 234-259. |
| [11] |
DAVIS M, LOGEMANN G, LOVELAND D W. A machine program for theorem-proving[J]. Communications of the ACM, 1962, 5(7): 394-397. DOI:10.1145/368273.368557 |
| [12] |
MARQUES-SILVA J P, SAKALLAH K A. GRA- SP—A new search algorithm for satisfiability[C]//IEEE/ACM International Conference on Computer-Aided Design, 1996. Iccad-96. IEEE: [s.n.], 1997: 220-227. https://link.springer.com/chapter/10.1007%2F978-1-4615-0292-0_7
|
| [13] |
ZHANG L, MADIGAN C F, MOSKEWICZ M H, et al. Efficient conflict driven learning in a Boolean satisfiability solver[C]//IEEE/ACM International Conference on Computer-Aided Design. IEEE Press: [s.n.], 2001: 279-285. http://dl.acm.org/citation.cfm?id=603095.603153
|
| [14] |
BRYANT R E. Graph-based algorithms for boolean function manipulation[J]. IEEE Trans Comput, 1986, C-35(8): 677-691. DOI:10.1109/TC.1986.1676819 |
| [15] |
GU T L, XU Z B. Ordered binary decision diagram and itsapplication[M]. Beijing: Science Press, 2009.
|
| [16] |
BRYANT R E. Symbolic Boolean manipulation with ordered binary decision diagrams[J]. ACM Computing Surveys, 1992, 24(3): 293-3l8. DOI:10.1145/136035.136043 |
 2018, Vol. 34
2018, Vol. 34 

