语音从人的口腔中发出时周围往往伴有各种各样的噪声, 例如, 马路上的汽车噪声、工厂和工地的机械轰鸣声, 房屋中的空调声、风扇声、日光灯的蜂鸣声、打字声、谈话声和小孩的哭闹声等。在语音信息的采集过程中, 难免会受到这些噪声的干扰。噪声不仅降低了语音的可懂度和清晰度, 甚至严重地影响着语音处理的准确性。因此, 减噪处理是语音处理的关键技术之一。
目前语音减噪方法主要有小波变换法[1]、MMSE法[2]、信号子空间法[3]、自适应滤波器减噪[4]、维纳滤波法[5]和谱减法[6]等。其中, 自适应滤波器减噪、维纳滤波法减噪和谱减法是使用最广泛的减噪算法。自适应滤波器减噪法有较快的收敛性和平稳性, 但计算量大, 需要不断的逐个点更新, 瞬时跟踪能力较弱; 维纳滤波法的适应面较广, 但不能用于噪声为非平稳的随机过程, 对于向量情况应用不方便; 相对于前两种方法, 由美国Utah大学的Boll[7]提出的谱减法由于具有引入约束条件少和运算量小的特点, 而被广泛采用。谱减法的研究起源于改进噪声中的线性预测(Linear Prediction, LP)分析, 而今已被发展成估计噪声频谱并进行减噪的经典算法。随着减噪研究的不断深入, 人们陆续提出了一些谱减法的变形形式, 其中1982年由Thomson提出的多窗谱估计的谱减法[8], 对Boll的谱减法进行了重要的改进[6]使得多窗谱估计的谱减法成为当前减噪处理的研究热点。因此, 本文通过分析谱减法及其改进方法中的过减因子和增益补偿因子, 研究了基于谱减法的藏语语音的减噪方法。
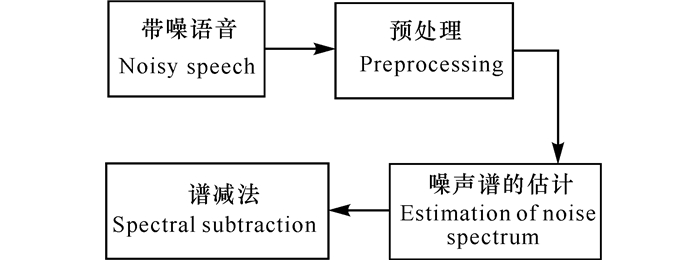
1 谱减法谱减法主要利用在无声期间统计得到的噪声方差来代替当前帧的噪声频谱, 其基本原理如图 1所示:
|
图 1 谱减法基本原理 Fig.1 The basic principle of spectral subtraction |
设语音信号的时间序列为x(n), 加窗分帧处理后得到第i帧语音信号为xi(m), 帧长为N。任何一帧语音信号xi(m)做DFT(离散傅里叶变换)后为
| $ {x_i}\left( k \right) = \sum\limits_{m = 0}^{N - 1} {{X_i}\left( m \right)} {\rm{exp}}\left( {j\frac{{2\pi mk}}{N}} \right){\rm{ }}\;\;\;\;\;k = 0,1, \ldots ,N - 1 。$ | (1) |
要对xi(k)求出每个分量的幅值和相角, 幅值是|xi(k)|, 它的相角是
| $ x_{{\rm{angle}}}^i\left( k \right) = {\rm{arctan}}\left[ {\frac{{lm({x_i}\left( k \right))}}{{{\rm{Re}}({x_i}\left( k \right))}}} \right]。$ | (2) |
已知前导噪声段时长为IS, 对应的帧数为NIS, 可以求出该噪声段的平均能量和谱减算法为
| $ D\left( k \right) = \frac{1}{{NIS}}\sum\limits_{i = 1}^{NIS} {|{x_i}\left( k \right){|^2}} 。$ | (3) |
| $ \begin{array}{l} {\left| {{{\hat x}_i}\left( k \right)} \right|^2} = \\ \left\{ \begin{array}{l} {\left| {{x_i}\left( k \right)} \right|^2} - \alpha \times D\left( k \right)\;\;\;\;\;{\left| {{x_i}\left( k \right)} \right|^2} \ge \alpha \times D\left( k \right)\\ \beta \times D\left( k \right)\;\;\;\;\;{\left| {{x_i}\left( k \right)} \right|^2} < \alpha \times D\left( k \right) \end{array} \right.。\end{array} $ | (4) |
谱减算法中α和β是两个常数, α称为过减因子; β称为增益补偿因子。求出了谱减后幅值为
传统的周期图法只用一个数据窗, 而Thomson提出的多窗谱估计的谱减法对同一数据序列用多个正交的数据窗分别求直接谱, 其次求平均得到谱估计, 因此可以得到较小的估计方差。Thomson使用的数据窗是一组相互正交的离散球序列(Discrete Prolate Spheroidal Sequences, DPSS), 也叫Slepian窗。多窗谱是一种比周期图法更准确的谱估计方法。多窗谱定义如下:
| $ {S^{mt}}\left( \omega \right) = \frac{1}{L}\sum\limits_{k = 0}^{L - 1} {{S^{mt}}\left( \omega \right)} , $ | (5) |
其中L为数据窗个数; Smt(ω)为第k个数据窗的谱:
| $ S_k^{mt}\left( \omega \right) = {\left| {\sum\limits_{n = 0}^{N - 1} {{a_k}\left( n \right)x\left( n \right){e^{ - jm\omega }}} } \right|^2}, $ | (6) |
其中x(n)为数据序列; N为序列长度; ak(n)为第k个数据窗, 满足多个数据窗之间相互正交:
| $ \begin{array}{*{20}{l}} {\sum {a_k}\left( n \right){a_j}\left( n \right) = 0\;\;\;{\rm{ }}k \ne j,}\\ {\sum {a_k}\left( n \right){a_j}\left( n \right) = 1{\rm{ }}\;\;k = j}。\end{array} $ | (7) |
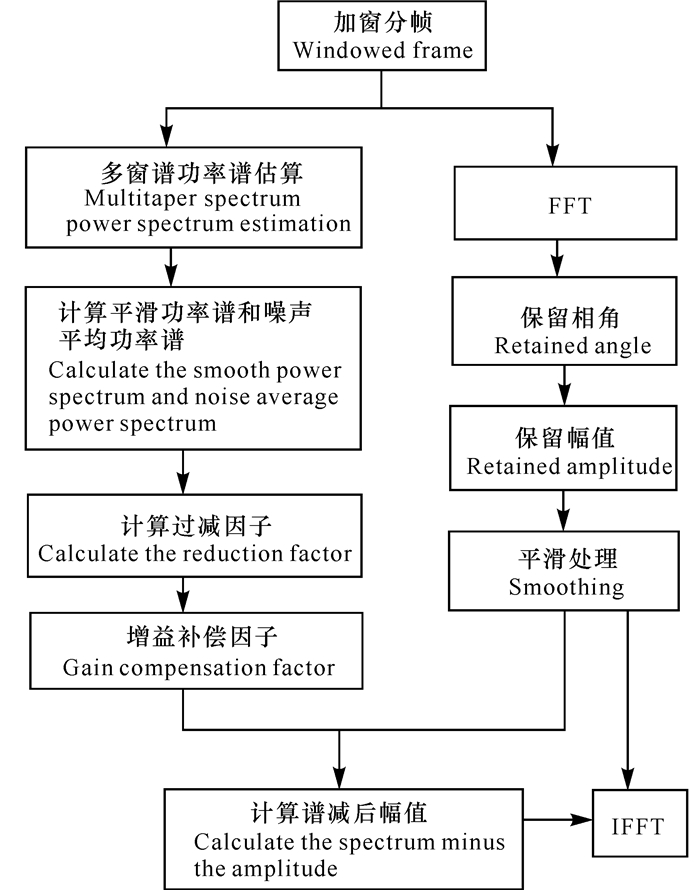
多窗谱估计中的过减因子和增益补偿因子两个参数对整个算法有着重要影响, 过减因子α主要影响语音谱的失真参数, 增益补偿因子β可以控制残留噪声的多少以及音乐噪声的大小[9]。藏语言文字是一种以辅音字母和元音字母为构件的拼音文字, 以音节为单位, 一般一个字为一个音节, 各音节间用音节符“·”分隔。本文为了从字、词、句及篇章等各个层次上研究考察藏语语音的减噪效果, 将藏语语音减噪算法设计如下(图 2):
|
图 2 基于谱减法的藏语语音减噪算法流程 Fig.2 The flow chart of Tibetan speech noise reduction algorithm based on spectral subtraction |
基于谱减法的藏语减噪算法具体步骤如下:
步骤1:读入语音文件, 消除直流分量, 幅值做归一化。
步骤2:设置初始噪声比后生成叠加高斯白噪声的带噪语音, 计算叠加噪后的信噪比。
步骤3:设置参数, 比如前导无话段长度、帧长、帧移、过减因子和增益补偿因子。
步骤4:计算多窗谱改进谱减法:
(1) 设置窗后开始分帧, 求帧数, 本实验中同样使用了汉明窗。
(2) 每帧语音信号计算快速傅里叶变换(FFT)。
(3) 求出正频率部分的幅值和相位角。
(4) 相邻帧之间做平滑处理, 然后计算平均幅值谱。
(5) 多窗谱法对每一帧数据进行功率谱估计, 对功率谱的相邻帧之间进行平滑处理。
(6) 前导无话段中求出噪声平均功率谱, 利用谱减关系计算出增益因子。
(7) 用增益补偿因子计算谱减后幅值, 幅值经快速傅里叶逆变换(IFFT), 求出谱减后语音序列。
步骤5:计算谱减后的信噪比, 输出信噪比与信噪增益, 合成减噪后语音。
3 结果与分析本文实验语料均来自藏语网站, 从大到小分为4个层次, 即包含631音节的篇章、平均包含11个音节的10个句子、20个多音节的词和短语、100单音节。语音的信噪比分别为-5 dB、0 dB、5 dB, 采样率为8 000 Hz、16 bit量化的纯净语音信号, 分别叠加高斯白噪声。
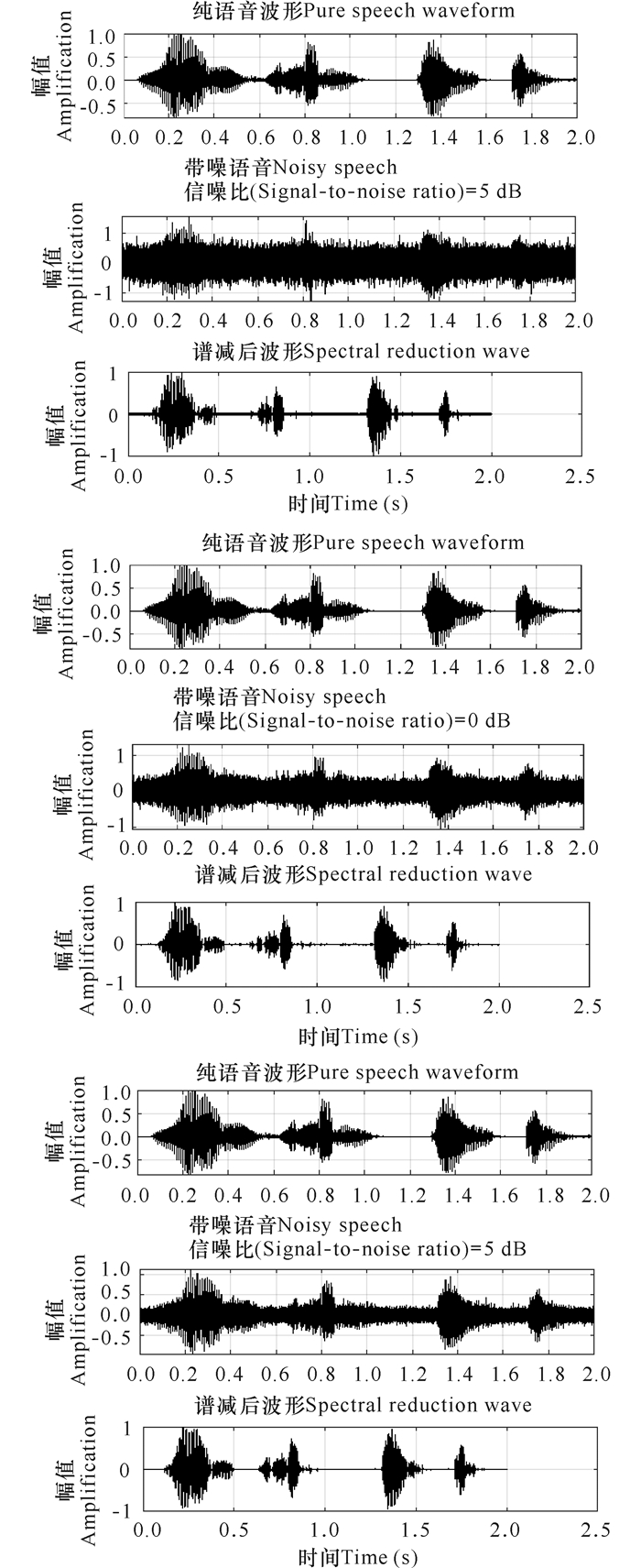
3.1 主观评测算法对-5 dB、0 dB、5 dB带噪语音处理后的结果、纯净语音以及谱减后的效果如图 3所示。不同信噪比时多窗谱减后的波形和纯净语音波形大同小异(图 3)。由6位测听员对4个语料在信噪比为0 dB下的减噪效果进行了测听, Mean Opinion Score(MOS)分值如表 1所示。句子减噪效果最好, 其次是多音节, 说明句子和多音节的减噪效果优于篇章和单音节的减噪效果(表 1)。
|
图 3 藏语多音节使用多窗谱估计的改进谱减法效果 Fig.3 Improved spectral subtraction effect of multisyllable using multitaper spectrum estimation in Tibetan |
| 表 1 MOS值 Table 1 MOS value |
适当地选择过减因子α和增益补偿因子β, 可以有效除掉噪声或控制残留噪声以及音乐噪声的大小。反之将导致语音失真[9]。通过实验发现, 藏语语音减噪中, α取值为1.8~3.0, β取值为0.001时较为合适。当过减因子α取1.7或者1.8时信噪比最高, α的值小于1.7或大于1.8时信噪比逐步减小; β=0.001时信噪比最高, β的值小于0.001或大于0.001时同样信噪比逐步减小。同时, 语料越大, 输出的信噪比就越提高。相对来说, 句子和多音节的减噪效果优于篇章和单音节的减噪效果。具体实验数据见表 2~4。
| 表 2 不同信噪比下调整过减因子 Table 2 Adjusting the reduction factor under different signal to noise ratio |
| 表 3 不同信噪比下调整增益补偿因子 Table 3 Adjusting the gain compensation factor under different signal to noise ratio |
| 表 4 相同信噪比下4部分藏语语料测算结果 Table 4 The calculation results of four parts of Tibetan language data under the same signal to noise ratio |
过减因子和增益补偿因子是决定谱减法减噪效果的重要参数, 本文通过统计分析藏语语音在不同信噪比下的过减因子α和增益补偿因子β, 研究了基于谱减法的藏语减噪算法, 得出较为理想的α和β的取值范围, 并发现句子和多音节的减噪效果优于篇章和单音节的减噪效果。
| [1] |
姚学锋, 吴震, 金观昌. 数字散斑相关法中的小波减噪分析[J]. 清华大学学报:自然科学版, 2001, 41(4/5): 108-111. YAO X F, WU Z, JIN G C. Wavelet denoising using the digital speckle correlation method[J]. J Tsinghua Univ:Sci & Tech, 2001, 41(4/5): 108-111. |
| [2] |
EPHRAIM Y, MALAH D. Speech enhancement using a mini-mum mean-square error short-time spectral amplitude estimator[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1984, 32(6): 1109-1121. |
| [3] |
EPHRAIM Y, VAN TREES H L. A signal subspace approachfor speech enhancement[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1995, 3(4): 251-266. |
| [4] |
宋知用. MATLAB在语音信号分析与语音合成中的应用[M]. 北京: 北京航空航天大学出版社, 2013: 184-194. SONG Z Y. The application of MATLAB in speech signal analysis and synthesis applications[M]. Beijing: Beihang University Press, 2013: 184-194. |
| [5] |
张青, 吴进. 基于多窗谱估计的改进维纳滤波语音增强[J]. 计算机应用与软件, 2017, 34(3): 67-70, 118. ZHANG Q, WU J. Improved wiener filter speech enhancement based on multi-taper spectrum estimation[J]. Computer Applications and Software, 2017, 34(3): 67-70, 118. |
| [6] |
武鹏鹏, 赵刚, 邹明. 基于多窗谱估计的改进谱减法[J]. 现代电子技术, 2008(12): 150-152. WU P P, ZHAO G, ZOU M. An improved spectral subtraction method based on multitaper estimation[J]. Modern Electronic Technology, 2008(12): 150-152. |
| [7] |
BOLL S. Suppression of acoustic noise in speech using spectral subtraction[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1979, 27(2): 113-120. |
| [8] |
HU Y, LOIZOU P C. Speech enhancement based on wavelet thresholding the multitaper spectrum[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 2004, 12(1): 59-67. |
| [9] |
[投稿]谱减法语音降噪原理[EB/OL].[2017-0-11]. http://blog.csdn.net/leixiaohua1020/article/details/47276353. [Submission] The principle of noise reduction in spectral subtraction[EB/OL].[2017-0-11].http://blog.csdn.net/leixiaohua1020/article/details/47276353. |
 2018, Vol. 34
2018, Vol. 34 


