2. 玉林师范学院物理科学与工程技术学院,广西玉林 537000
2. Institute of Physics Science and Engineering Technology, Yulin Normal University, Yulin, Guangxi, 537000, China
【研究意义】 现代材料的性能,特别是超塑性材料、纳米晶材料和复合材料的性能,极依赖于其内部的界面位错结构[1-3]。晶界结构的转变就是这一过程的重要体现。当体系温度接近熔点时,由于晶界处的熔点温度低于完整晶粒的熔点温度,会出现晶界预熔化现象[4-10]。由于晶界通常只有几个原子层厚度,在现有的实验条件下难以直接观察到晶界预熔化现象,因此可采用强大的计算机模拟技术来弥补实验的不足。【前人研究进展】已有学者采用分子动力学方法研究晶界在材料块体熔点附近的预熔化行为,模拟结果均表明:施加外应变时,应变效应导致热力学熔点降低,促进表面熔化进程。2002年Elder等[11-12]从经典密度泛函理论出发,提出了晶体相场(PFC)模型。该模型采用具有周期对称性的原子密度作为序参量,其自由能函数包含了周期对称性、弹性能以及各向异性等特点。因此,能够在原子尺度模拟扩散时间尺度的微观结构的演化现象[13-18]。2008年Berry等[19]应用由Ramakrishnan等提出的局域密度泛函理论的模型,推导出纯物质三维BCC结构的无量纲形式的PFC模型。【本研究切入点】目前,结合自由能曲线研究应变作用下三维位错的预熔化现象的研究还未见报道。【拟解决的关键问题】运用PFC模型,研究外应变作用下的位错预熔化现象,在BCC晶体中观察位错和晶界的预熔现象,揭示晶界预熔化的机理。
1 PFC模型 1.1 自由能函数在三维晶体预熔的PFC模型中,其无量纲自由能函数形式为[20]
| $ F=\int{{\rm{d}}\mathit{r}[\frac{B1}{2}{{n}^{2}}+\frac{Bs}{2}n\left( 2{{\nabla }^{2}}+{{\nabla }^{4}} \right)n-w\frac{{{n}^{3}}}{6}+\frac{{{n}^{4}}}{12}], } $ | (1) |
其中n=(ρ-ρ0)/ρ0表示相对原子密度差,ρ0表示平均原子密度,ρ表示局部原子密度;B1和Bs是根据接近液体凝聚点的二体相关函数来决定的参量,温度正比于ΔB=B1-Bs;w与三体关系函数有关。因此,ΔB=B1-Bs被看成是与温度成比例,整个系统的固-液转换过程是通过改变ΔB(或Bl)而进行的。方程(1)的能量极小值的体心立方原子密度单模近似解为
| $ \ \ \ \ n\left( r \right)=A(\rm{cos}~\mathit{qx}~\rm{cos}~\mathit{qy}+\rm{cos}~\mathit{qx}~\rm{cos}~\mathit{qz}+\\ \rm{cos}~\mathit{qy}~\rm{cos}~\mathit{qz})。$ | (2) |
由于n和ρ是保守场的变量,因此保守场的动力学方程可写为
| $ \begin{align} &\ \ \ \ \frac{\partial n}{\partial t}={{\nabla }^{2}}~\frac{\delta F}{\delta n}={{\nabla }^{2}}n{{B}_{l}}+{{\nabla }^{2}}n{{B}_{s}}\left( 2{{\nabla }^{2}}+{{\nabla }^{4}} \right)- \\ &{{\nabla }^{2}}w\frac{{{n}^{2}}}{2}+{{\nabla }^{2}}\frac{{{n}^{3}}}{3} 。\end{align} $ | (3) |
式中t表示时间变量,δ是变分符号。采用半隐式Fourier谱方法进行数值计算,详细步骤见文献[21]。
1.2 样品参数设置设置为三维单晶体系,样品的尺寸区域为V= (256Δx)3 =(28a)3,其中a为晶格常数是a=8.923 7,满足周期边界条件;取向角为θ=1°;空间步长为Δx=0.976 031;时间步长为Δt=0.5;设置
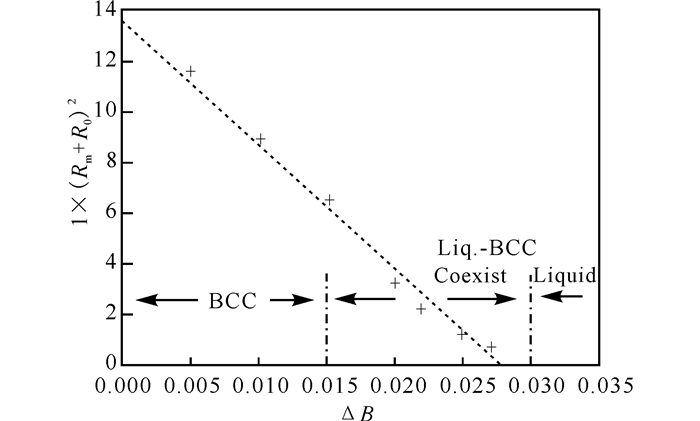
实验发现,熔解温度与围绕着位错核心的溶解区域半径Rm有关,即1/Rm2与ΔB成线性关系[15]。我们首先设置一个补偿量R0, 当温度为零时其与位错的核心尺寸有关,其中R0和Rm都是以晶格常数a做为单位,图 1为1/(Rm+R0)2与ΔB的关系曲线,此时得到最佳拟合结果R0=0.028 12 a,我们将这个曲线称为位错熔解半径与温度关系曲线。在图 1中可以观察到,整个系统按固液区分可以分为3种状态:固态、固-液共存态以及液态。如图 1中的BCC范围,当ΔB小于0.015 0,此时是整个系统的温度非常低的时候,系统处于固态;当ΔB大于0.021 2,此时晶界的位错将出现明显的预熔化现象,一直到ΔB为0.029 6附近,预熔现象进一步加剧将出现大量的熔解,系统处于固-液共存态;当ΔB大于0.030, 系统最终变纯液态。因此,为了研究在固-液共存区域处,不同温度下晶界在外加应力作用下的运动过程,本实验的体系温度的设定可参考图 1。
|
图 1 位错熔解半径与温度的关系曲线 Fig.1 The curve of the relationship between the dislocation melted radius and temperature |
实验样品的制备分为两个阶段:第一阶段是制备出处于固-液共存区域,不同温度条件下的单晶样品,目的是为了使其处于预熔或者熔解状态。对于样品1和样品2,按如下表 1中的数据选取样品的温度参数值。利用PFC方法设置样品,温度参数如表 1所示,并在该温度弛豫5 000步达到平衡。第二阶段为加应力过程,采用等体积条件假设,设e为无量纲应变速率,其中e=6×10-6,应变为E=enΔt,n为步数。
| 表 1 样品参数 Table 1 Sample parameters |
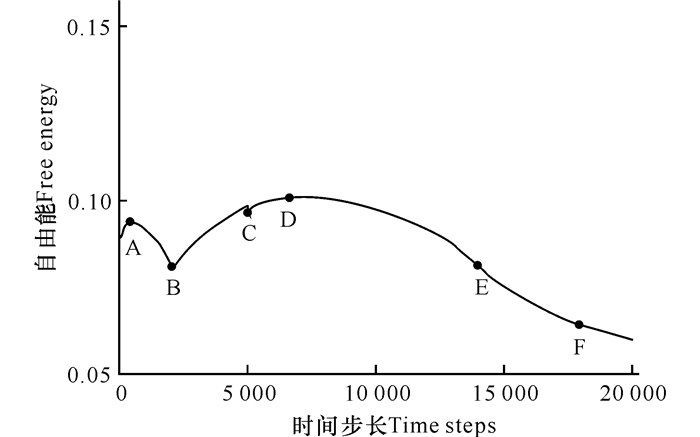
由图 2可见,样品升温过程中自由能先升高到A点,之后弛豫,出现位错消耗能量, 自由能降到B点。在加应力过程中,自由能上升到C点,位错攀移运动,自由能升高,并在D点达到最大值。随后由于位错对的湮没消耗大量能量,自由能降低。由图 3可以看出,在升温过程中出现位错对;随着外应力的施加,位错对出现了滑移现象,它们相互靠近,最终湮没,形成一个完整的晶粒。
|
图 2 样品1(ΔB=0.023 0)自由能曲线图 Fig.2 The free energy curve of the sample 1 (ΔB=0.023 0) |

|
(a)tA=456;(b)tB=2 041;(c)tC=5 001;(d)tD=6 608;(e)tE=14 000;(f)tF=18 000 图 3 样品1(ΔB=0.023 0)位错熔解截面图 Fig.3 The dislocation melting section of the sample 1 (ΔB=0.023 0) |
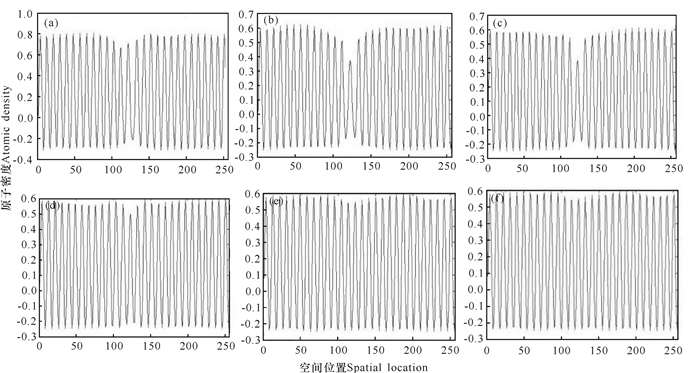
由图 4可见,中心线上的原子密度随着原子排列的空间位置变化而变化,且原子排列呈周期性,所以原子密度分布也体现出周期性变化,起初幅度比较均匀, 而后由于温度的升高出现位错对,此时对应的原子密度曲线的中心处幅度不断变小,之后随着应力的施加, 位错湮没形成完整晶界,这时原子密度分布的幅度又趋于平稳。
|
(a)tA=456;(b)tB=2 041;(c)tC=5 001;(d)tD=6 608;(e)tE=14 000;(f)tF=18 000 图 4 样品1(ΔB=0.023 0)位错竖直中心线上的时间平均数密度n Fig.4 The time average density n of the dislocation vertical center line of the samples 1 (ΔB=0.023 0) |
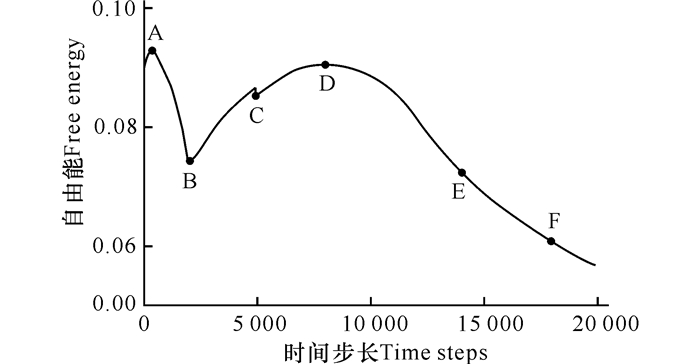
根据样品2的自由能曲线(图 5),在样品制备过程中,自由能由于升温先升高到A点,之后出现位错消耗能量, 自由能下降到B点,然后在弛豫过程中能量慢慢上升到C点;在加应力过程中,位错运动, 自由能依旧升高并在D点达到最大值,随后由于位错对的连通需要消耗大量能量, 自由能慢慢降低。
|
图 5 样品2 (ΔB=0.026 0)自由能曲线 Fig.5 The free energy curve of the sample 2(ΔB=0.026 0) |
由图 6可以看出,在升温过程中出现位错对;随着外应力的施加,样品2(ΔB=0.026 0)与样品1(ΔB=0.023 0)不同:位错对出现滑移现象并相互靠近的结果不再是形成一个完整的晶界,而是发生了连通变为一个圆形,且位错对在应力的作用下引起了熔化区域的更进一步增加,熔解面积明显增加,位错的熔解半径也进一步扩大。

|
(a)tA=372;(b)tB=2 091;(c)tC=5 001;(d)tD=7 842;(e)tE=14 000;(f)tF=18 000 图 6 样品2 (ΔB=0.026 0)位错熔解截面图 Fig.6 The dislocation melting section of the sample 2 (ΔB=0.026 0) |
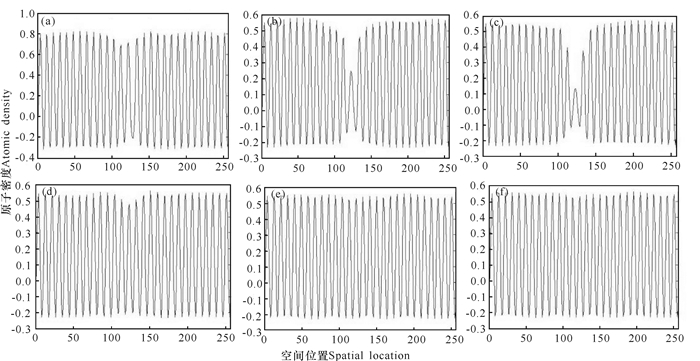
根据图 7,中心线上的时间平均数密度随着原子排列的空间结构的变化而变化。由图 7可知原子排列呈周期性,所以时间平均数密度也出现周期性变化,起初幅度比较平均;而后由于温度的升高出现位错对,此时对应的原子密度曲线的中心处幅度不断变小,之后随着应力的施加,位错对的湮灭形成完整晶界的原子密度的幅度又趋于平稳。
|
(a)tA=372;(b)tB=2 091;(c)tC=5 001;(d)tD=7 842;(e)tE=14 000;(f)tF=18 000 图 7 样品2(ΔB=0.026 0)位错竖直中心线上的时间平均数密度n Fig.7 The time average density n of the dislocation vertical center line of the samples 2 (ΔB=0.026 0) |
本研究运用PFC模型研究外应变作用下BCC晶体中晶界和位错的预熔化现象,结果表明:
(1) 当温度较低时,位错出现明显熔解现象,并且随着温度的升高,位错熔解的区域不断扩大,在接近熔点温度时, 晶界处的位错首先诱发晶界出现预熔化现象; 当熔解趋于稳定后, 在应力作用下开始出现位错滑移现象,同一水平直线上的一组位错对相互靠近,最终湮没变为一个完整晶界。
(2) 当温度较高时,位错出现更加明显的熔解,并且随着温度的升高,位错熔解区域也不断扩大,体系的温度影响并决定位错的熔解。体系温度越高,位错处的熔解就越容易进行。
| [1] |
STRAUMAL B B, ZIęBA P, GUST W. Grain boundary phase transitions and phase diagrams[J]. International Journal of Inorganic Materials, 2001, 3(8): 1113-1115. DOI:10.1016/S1466-6049(01)00108-8 |
| [2] |
STRAUMAL B, KOGTENKOVA O, PROTASOVA S, et al. Wetting and premelting of triple junctions and grain boundaries in the Al-Zn alloys[J]. Materials Science and Engineering:A, 2008, 495(1/2): 126-131. |
| [3] |
LUO J. Liquid-like interface complexion:From activated sintering to grain boundary diagrams[J]. Current Opinion in Solid State and Materials Science, 2008, 12(5/6): 81-88. |
| [4] |
ALSAYED A M, ISLAM M F, ZHANG J, et al. Premelting at defects within bulk colloidal crystals[J]. Science, 2005, 309(5738): 1207-1210. DOI:10.1126/science.1112399 |
| [5] |
TALLON J L. Premelting near crystal defects[J]. Nature, 1978, 276(5690): 849. |
| [6] |
BARTIS F J. Pre-melting near crystal dislocations[J]. Nature, 1977, 268(5619): 427-428. DOI:10.1038/268427a0 |
| [7] |
OXTOBY D W. New perspectives on freezing and melting[J]. Nature, 1990, 347(6295): 725-730. DOI:10.1038/347725a0 |
| [8] |
PUSEY P N. Freezing and melting:Action at grain boundaries[J]. Science, 2005, 309(5738): 1198-1199. DOI:10.1126/science.1116597 |
| [9] |
HSIEH T E, BALLUFFI R W. Experimental study of grain boundary melting in aluminum[J]. Acta Metallurgica, 1989, 37(6): 1637-1644. DOI:10.1016/0001-6160(89)90130-2 |
| [10] |
卢柯, 生红卫, 金朝晖. 晶体的熔化和过热[J]. 材料研究学报, 1997, 11(6): 658-665. LU K, SHENG H W, JIN Z H. Melting and superheating of crystals[J]. Chinese' Journal of Materials Research, 1997, 11(6): 658-665. |
| [11] |
ELDER K R, KATAKOWSKI M, HAATAJA M, et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88(24): 245701. DOI:10.1103/PhysRevLett.88.245701 |
| [12] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70(5): 051605. DOI:10.1103/PhysRevE.70.051605 |
| [13] |
罗志荣, 卢成健, 高英俊. 相场法研究初始微结构对晶粒长大的影响[J]. 广西科学, 2016, 23(5): 432-436, 442. LUO Z R, LU C J, GAO Y J. Phase field study on effect of initial microstructure on grain growth[J]. Guangxi Sciences, 2016, 23(5): 432-436, 442. |
| [14] |
刘瑶, 袁龙乐, 卢强华, 等. 晶体相场模拟取向角对晶界湮没过程的影响[J]. 广西科学, 2016, 23(5): 437-442. LIU Y, YUAN L L, LU Q H, et al. Phase-field-crystal simulation of effect of different orientation angle on annihilation of grain boundary[J]. Guangxi Sciences, 2016, 23(5): 437-442. |
| [15] |
杨瑞琳, 刘瑶, 胡绪志, 等. 双位错滑移运动的晶体相场模拟[J]. 广西科学, 2016, 23(5): 443-447. YANG R L, LIU Y, HU X Z, et al. Phase-field-crystal simulation of double dislocation gliding[J]. Guangxi Sciences, 2016, 23(5): 443-447. |
| [16] |
黄世叶, 李胜男, 胡绪志, 等. 晶界位错运动的空位晶体相场模拟[J]. 广西科学, 2016, 23(5): 459-464. HUANG S Y, LI S N, HU X Z, et al. Vacancy phase-field-crystal simulation of dislocation motion of grain boundary[J]. Guangxi Sciences, 2016, 23(5): 459-464. |
| [17] |
叶里, 胡绪志, 黄礼琳, 等. 拉应力作用下晶界位错运动过程的晶体相场模拟[J]. 广西科学, 2016, 23(5): 470-473, 484. YE L, HU X Z, HUANG L L, et al. Phase-field-crystal simulation of grain boundary dislocation motion under tensile stress[J]. Guangxi Sciences, 2016, 23(5): 470-473, 484. |
| [18] |
叶里, 黄礼琳, 孔令一, 等. 晶体弹性行为的晶体相场模拟[J]. 广西科学, 2016, 23(5): 474-477. YE L, HUANG L L, KONG L Y, et al. Phase-field-crystal simulation for elastic behavior of crystals[J]. Guangxi Sciences, 2016, 23(5): 474-477. |
| [19] |
BERRY J, ELDER K R, GRANT M. Melting at dislocations and grain boundaries:A phase field crystal study[J]. Physical Review B, 2008, 77(22): 224114. DOI:10.1103/PhysRevB.77.224114 |
| [20] |
卢成健, 路哲, 刘文祥, 等. 三维晶体相场法模拟位错的预熔及熔解[J]. 广西物理, 2013, 34(2): 8-11. LU C J, LU Z, LIU W X, et al. Three-dimensional phase field crystal simulation of dislocation pre-melting and melting[J]. Guangxi Physics, 2013, 34(2): 8-11. |
| [21] |
YU Y M, BACKOFEN R, VOIGT A. Morphological instability of heteroepitaxial growth on vicinal substrates:A phase-field crystal study[J]. Journal of Crystal Growth, 2011, 318(1): 18-22. DOI:10.1016/j.jcrysgro.2010.08.047 |
 2017, Vol. 33
2017, Vol. 33 


