2. 玉林师范学院物理科学与工程技术学院,广西玉林 537000
2. Institute of Physics Science and Engineering Technology, Yulin Normal University, Yulin, Guangxi, 537000, China
【研究意义】纳米晶体材料由于具有独特的结构特征(含有大量的内界面),为深入研究固体内界面结构与性能提供了良好条件,以及表现出一系列优异的理化及力学性能,所以纳米晶体材料是近年来的研究热点。材料在介观和宏观尺度上的性能在很大程度上由复杂的拓扑几何缺陷所决定[1]。虽然之前已经建立了大量的模型来研究晶体相的形核和生长等现象,但很难建立起一种包含多个尺度的模型。最近,Elder提出了一种新的晶体相场模型。它的优势在于该模型在原子长度上以自然方式将弹性和塑性变形结合起来,在扩散时间尺度上使人们能够获得比分子动力学(MD)方法大得多的时间尺度,被视作在界面计算领域的最新方法。晶体相场(PFC)方法的优势就在于它在MD模拟方法和传统相场方法之间建立了桥梁,能够弥补分子模拟方法和相场之间的不足[2]。【前人研究进展】晶体相场方法不同于传统的相位场(PF)[3-7]方法中序参量的空间均匀的相平衡和平滑变化的界面[8]。目前PFC方法已经成功模拟了非平衡晶体生长[9]、在纳米薄膜上的外延岛形成[10]、晶界位错预熔化[11]、异质外延生长[12]、晶体结构的相转变[13]、韧性材料的微裂纹扩展与连通[14]、位错运动的空位模拟等[15-17],对于实验也有指导意义。为了扩大晶体相场模型的适用范围,很多学者对该模型做了大量的改进工作,取得了很大进展。如Wu等[18]提出的双模PFC模型能够很好描述正方相、面心立方相等复杂的晶体点阵结构。【本研究切入点】对于正方相的研究,虽然已经有研究团队做过类似模拟,例如六角相向正方相的转变[19]或外加应力下晶界位错运动的研究,但是,应用PFC模型来详细研究大角度正方相的位错运动还未见报道。【拟解决的关键问题】应用双模PFC模型来研究晶体的正方相大角度取向角的晶界湮没过程,揭示施加应力后晶界位错运动的规律。
1 PFC模型PFC模型通过引入具有周期结构特征的原子密度相场变量构建自由能密度函数,能够揭示晶体学结构特征以及原子尺度的行为[19]。在晶体相场(PFC)模型中,晶体密度场基本上是以单傅立叶模式描述的,即正弦密度波。它已被应用于大规模的固体动力学数值研究。
根据文献[2],用原子密度函相场变量,其表达式[20]可写为
| $ \rho ={{\sum }_{n, m}}{{a}_{n, m}}{{e}^{i\mathit{\vec{G}}\cdot \vec{r}}}+{{\rho }_{0}}, $ | (1) |
式子右边第一项是原子的周期排列特征项,第二项是反映均匀相的原子密度。Wu等[18]提出的双模PFC模型,无量纲化的自由能函数形式为
| $ \begin{align} & \ \ \ F=\int \text{d}\mathit{V}\text{ }\!\![\!\!\text{ }\frac{\rho }{\text{2}}\{-\varepsilon \text{+}{{\left( {{\nabla }^{\text{2}}}\text{+1} \right)}^{\text{2}}}\times [{{\mathit{R}}_{\text{1}}}\text{+(}{{\nabla }^{\text{2}}}\text{+} \\ & {{\mathit{Q}}^{\text{2}}}_{\text{1}}{{)}^{\text{2}}}]\}\mathit{\rho }+\frac{{{\rho }^{4}}}{4}]=\int{{{F}_{0}}\text{d}\mathit{V}}, \\ \end{align} $ | (2) |
其中F0为自由能密度函数,ρ为无量纲的原子密度场,ε是与温度有关的参数;Q1是次近邻倒格矢的模与最近邻倒格矢的模之比,对于二维正方晶格来说,
| $ \begin{align} &\ \ \ {{F}_{0}}=\frac{4-\varepsilon }{2}\rm{ }{{\rho }^{2}}+\frac{\rho }{2}\rm{ }({{\nabla }^{8}}+6{{\nabla }^{6}}+13{{\nabla }^{4}}+ \\ &12{{\nabla }^{2}})\rho +\rm{ }\frac{{{\rho }^{4}}}{4}, \\ \end{align} $ | (3) |
式中(∇2)n为高阶的Laplace算子,n=2, 3, 4。
2 计算方法 2.1 动力学方程与数值计算保守的原子密度场变量的演化可用与时间相关的Cahn-Hilliard动力学方程描述:
| $ \frac{\partial \rho }{\partial t}={{\nabla }^{2}}\frac{~\delta {{F}_{0}}}{\delta \rho }, $ | (4) |
可以利用式(3)将动力学方程(4)写为
| $ \begin{align} &\ \ \ \ \ \frac{\partial \rho }{\partial t}\rm{ }=[{{\nabla }^{10}}+6{{\nabla }^{8}}+13{{\nabla }^{6}}+12{{\nabla }^{4}}+(4-\\ &\varepsilon ){{\nabla }^{2}}]\rho +{{\nabla }^{2}}{{\rho }^{3}}, \\ \end{align} $ | (5) |
由于方程(5)是高阶的非线性偏微分方程,本研究将采取半隐式伪谱法[20]来求解该动力学方程。在本研究中,将空间步长Δx和Δy均取为π/4,时间步长为0.5,模拟区域为512Δx+512Δy。正方相的单相原子密度函数形式为
| $ \begin{align} &\ \ \ \ \ \rho \approx {{\rho }_{0}}+2{{A}_{s}}\left( \rm{cos}{{\mathit{q}}_{\mathit{s}}}\mathit{x}\rm{cos}{{\mathit{q}}_{\mathit{s}}}\mathit{y} \right)+ \\ &4{{B}_{s}}\left( \rm{cos}{{\mathit{q}}_{\mathit{s}}}\mathit{x}\rm{cos}{{\mathit{q}}_{\mathit{s}}}\mathit{y} \right), \\ \end{align} $ | (6) |
式(6)中的参数As、Bs见文献[19]。
2.2 应变施加本研究选取的参数为(r,ρ_0)=(0.15, -0.21),旋转角度为40°。应变施加将采取等面积不变模型[5, 21],即ΔxΔy=Δx′Δy′,其中Δx、Δy是变形前的空间步长,Δx′、Δy′是变形后的空间步长。设
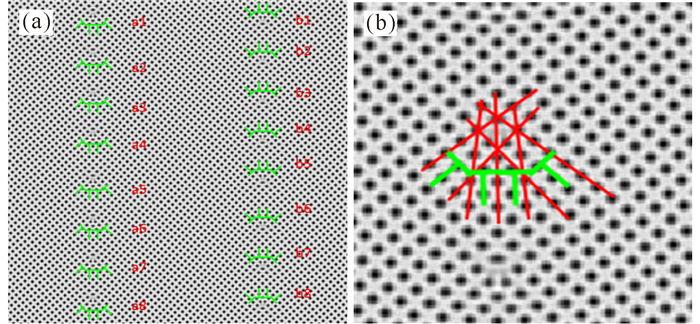
图 1a为弛豫7万步后的样品。由图 1a可见,对称倾侧晶界的夹角为大角度时,晶界位错排列比较整齐。在稳定的两侧晶界都形成若干刃型位错。这些刃型位错可以分为两组,所属同列晶界,位错方向相同,所属异侧晶界,位错方向相反。晶界上分别由8对位错对(标记为a1~a8和b1~b8)排列而成。每个位错对都由两个主位错,两个副位错组成,其中,两侧的为主位错,中间的为副位错。图 1b是位错a6的放大细节图。
|
图 1 样品的晶界位错排列(a)和放大的位错组态图(b) Fig.1 Grain boundary dislocation arrangement of the sample (a) and the diagram of enlarged dislocation configuration (b) |
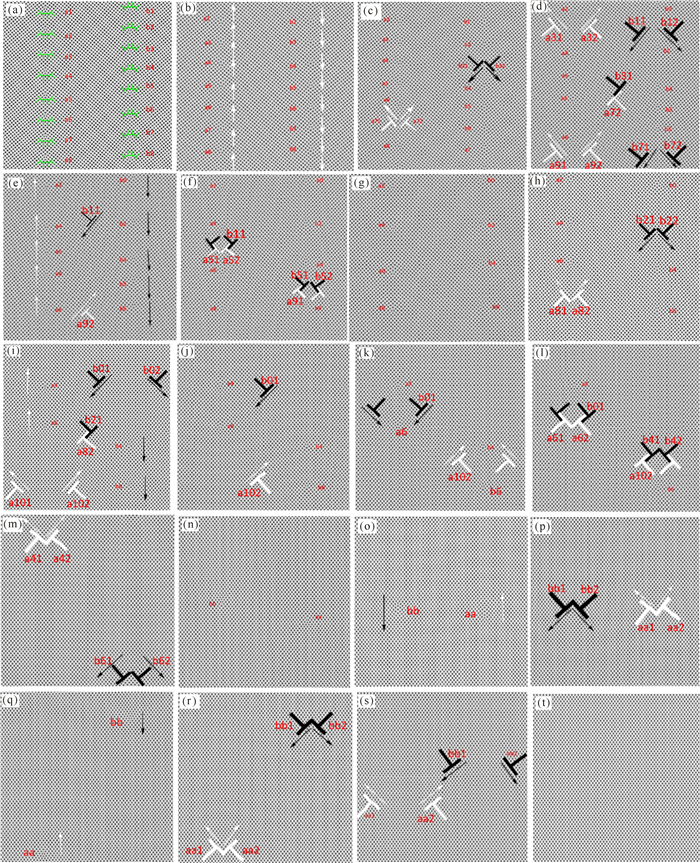
在外加应力作用下,整个体系的畸变能不断增加(图 2a~c段),总的自由能上升,当应力达到一定值时导致位错分解发生滑移(图 3c),使得自由能降低(图 2c~e段)。随着应变的不断增加,当施加的应变足以克服晶界的额外阻力时,左右两条晶界中部分位错有序地从晶界发射,余下的位错则将继续沿着晶界攀移;从晶界发射的位错,继续滑移运动直至与其极性相反的位错相遇发生湮没。详细的晶界湮没过程如图 3a~t所示。

|
图 2 自由能变化曲线 Fig.2 The curve of free energy |
|
(a)ε=0;(b)ε=0.043 8;(c)ε=0.474 0;(d)ε=0.053 4;(e)ε=0.058 5;(f)ε=0.070 5;(g)ε=0.071 4;(h)ε=0.090 0;(i)ε=0.097 2;(j)ε=0.099 6;(k)ε=0.108 0;(l)ε=0.109 5;(m)ε=0.129 9;(n)ε=0.148 5;(o)ε=0.156 6;(p)ε=0.159 6;(q)ε=0.176 4;(r)ε=0.186 9;(s)ε=0.193 5;(t)ε=0.196 8 图 3 40°取向角晶界位错运动演化过程 Fig.3 The evolutionary process of dislocation motion at 40° of orientation angle |
图 3中每个点均与图 2中的点一一对应。由图 3可见,40°晶界的湮没过程主要分为5个过程:1)晶界位错攀移(图 3a~c);2)位错分解,滑移,湮没[22-23](图 3c~g);3)剩下一部分晶界位错继续攀移,分解,滑移,湮没(图 3h~l);4)剩下另一部分晶界位错分解,滑移,形成新的位错(图 3m~n,p~q);5)最后剩下的位错分解,滑移,湮没(图 3r~t)。在图 3a~b晶界位错只发生攀移,对应图 2自由能曲线在升高,所以可以说明攀移会使整体的自由能升高;同样在图 3r~s只发生滑移,对应图 2自由能降低,可以理解为位错滑移会使体系的自由能下降。当ε=0.043 8时(图 3b),一些位错已经完成攀移,还有部分位错正在开始攀移。随着应变量的增加,位错沿着晶界攀移的数目也就越来越多,对应图 2自由能在上升。当ε=0.047 4时(图 3c),应力值达到一定值后,a7、b3两对位错发射,并进行滑移,对应图 2自由能曲线c~e段,自由能开始下降。当ε=0.053 4时(图 3d),a3、b1、a9、b7 4对位错都已分解,另外位错b31与a72滑移后在晶粒内部相遇并湮没,可由图 2对应曲线中看到自由能大幅降低。当ε=0.058 5时(图 3e),位错攀移,左边的位错向上攀移,右边的向下攀移,同时位错a9、b1分裂。当ε=0.070 5时(图 3f),位错b1滑移到a5处,与a5发生湮没,与此同时,位错a9滑移至b5处,在b5处与之结合湮没,这两组均属于位错在晶界上湮没合并。当ε=0.071 4时(图 3g),余下的位错在晶界上又组成整齐的晶界。可以看到在图上剩余4组位错,a2、a4、a6、a8与b0、b2、b4、b6。在图 2自由能曲线e~f可以看到有一段相对平缓的区域,称之为平台期。之所以形成平台期是因为在这个期间部分位错滑移和部分位错攀移,攀移是自由能升高,而滑移使自由能降低,当它们达到平衡时,自由能变化保持稳定,呈现平台期。当ε=0.090 0时(图 3h),随着外加应变的逐步增加,晶界上的位错再次发射,对应的本段自由能曲线即将呈下降趋势。当ε=0.097 2时(图 3i),a8和b2位错在晶粒内部结合,与此同时b0与a10发射位错,所以对应的图 2自由能曲线h~i段一直处于下降状态。图 3j~k点位错进行攀移和滑移,有4对位错在攀移,1对位错在滑移,即攀移占主导,所以相应的图 2自由能曲线j~k段有一定程度的上升阶段。在图 3k点b0、a10位错继续滑移湮没,当ε=0.109 5时(图 3l),b0位错滑移穿过晶粒内部,直到在对面晶界的a6处与之结合湮没,同样a10滑移到b4处,与之结合湮没,所以由图 2的l点可以看到,自由能降低至最低点。此时,只剩下1对位错。如图 3m,再次重复之前行为位错发射,位错滑移,但是在ε=0.148 5时(图 3n),两两位错滑移到一起,形成了新的位错,根据它的位错方向,我们把它们命名为bb、aa位错。从图 3n~o可以看到,左侧位错bb在向下攀移,右侧位错aa在向上攀移,对应图 3n~o段自由能在升高。图 3m~n与图 3p~q重复同样的行为,均为位错滑移到某个位置形成新的位错对,对应图 2自由能曲线呈相同趋势,即先上升再下降。当ε=0.186 9时(图 3r),图中仅剩的两个位错对分解,当ε=0.193 5时(图 3s),位错bb1与aa2即将滑移到晶界内部进行湮没。当ε=0.196 8时(图 3t),样品将变为完整的单晶,没有任何位错。由于湮没的位错数目越多,自由能曲线的谷越深;晶界同时攀移的位错数目越多,自由能曲线的峰越高[24],所以图 2a~c段的曲线峰最高。
4 结论PFC模型能较好地用于研究大角度的正方相的位错在施加应力作用下的运动。本研究晶界上每组位错都由4个位错组成1个位错对。晶界的湮没过程主要特征如下:开始时位错沿晶界攀移,随后晶界发生位错分解并发射,位错运动方式由攀移转为滑移;滑移位错与其他位错在晶内相遇发生湮没,其余晶界位错进行攀移,再次出现晶界位错分解发射位错,位错滑移穿过晶界内部,到达对面晶界处发生湮没;最后剩下的位错又发生分解,滑移,湮没,形成完整单晶。在位错的运动过程中,两个副位错随各自临近主位错运动,在主位错相互湮没时,各自携带的副位错由于方向相反,也两两湮没。在40°晶界位错运动过程中,自由能曲线可能出现一段平台期,产生原因是位错攀移导致的自由能上升与位错滑移导致的自由能下降的能量达到平衡。
| [1] |
卢柯, 周飞. 纳米晶体材料的研究现状[J]. 金属学报, 1997, 33(1): 99-106. LU K, ZHOU F. Recent research progress on nanocrystalline materials[J]. Acta Metallurgica Sinica, 1997, 33(1): 99-106. |
| [2] |
EMMERICH H, GRÁNÁSY L, LÖWEN H. Selected issues of phase-field crystal simulations[J]. The European Physical Journal Plus, 2011, 126: 102. DOI:10.1140/epjp/i2011-11102-1 |
| [3] |
CHEN L Q. Phase-field models for microstructure evolution[J]. Annual Review of Materials Research, 2002, 32(1): 113-140. DOI:10.1146/annurev.matsci.32.112001.132041 |
| [4] |
JAATINEN A, ALA-NISSILA T. Eighth-order phase-field-crystal model for two-dimensional crystallization[J]. Physical Review E, 2010, 82(6): 061602. DOI:10.1103/PhysRevE.82.061602 |
| [5] |
高英俊, 罗志荣, 胡项英, 等. 相场方法模拟AZ31镁合金的静态再结晶过程[J]. 金属学报, 2010, 46(10): 1161-1172. GAO Y J, LUO Z R, HU X Y, et al. Phase field simulation of static recrystallization for AZ31 Mg alloy[J]. Acta Metallurgica Sinica, 2010, 46(10): 1161-1172. |
| [6] |
张宪刚, 宗亚平, 吴艳. 相场再结晶储能释放模型与显微组织演变的模拟研究[J]. 物理学报, 2012, 61(8): 467-475. ZHANG X G, ZONG Y P, WU Y. A model for releasing of stored energy and microstructure evolution during recrystallization by phase-field simulation[J]. Acta Physica Sinica, 2012, 61(8): 467-475. |
| [7] |
魏承炀, 李赛毅. 温度梯度对晶粒生长行为影响的相场模拟[J]. 物理学报, 2011, 60(10): 100701. WEI C Y, LI S Y. Effect of temperature gradient on grain growth behavior from phase field simulations[J]. Acta Physica Sinica, 2011, 60(10): 100701. DOI:10.7498/aps.60.100701 |
| [8] |
HIROUCHI T, TAKAKI T, TOMITA Y. Developme-nt of numerical scheme for phase field crystal deformation simulation[J]. Computational Materials Science, 2009, 44(4): 1192-1197. DOI:10.1016/j.commatsci.2008.08.001 |
| [9] |
TANG S, YU Y M. Phase-field-crystal simulation of nonequilibrium crystal growth[J]. Physical Review E, 2014, 89(1): 012405. DOI:10.1103/PhysRevE.89.012405 |
| [10] |
ELDER K R, HUANG Z F. A phase field crystal study of epitaxial island formation on nanomembranes[J]. Journal of Physics:Condensed Matter, 2010, 22(36): 364103. DOI:10.1088/0953-8984/22/36/364103 |
| [11] |
BERRY J, ELDER K R, GRANT M. Melting at dislocations and grain boundaries:A phase field crystal study[J]. Physical Review B, 2008, 77(22): 224114. DOI:10.1103/PhysRevB.77.224114 |
| [12] |
陈成, 陈铮, 张静, 等. 晶体相场法模拟异质外延过程中界面形态演化与晶向倾侧[J]. 物理学报, 2012, 61(10): 108103. CHEN C, CHEN Z, ZHANG J, et al. Simulation of morphological evolution and crystallographic tilt in heteroepitaxial growth using phase-field crystal method[J]. Acta Physica Sinica, 2012, 61(10): 108103. DOI:10.7498/aps.61.108103 |
| [13] |
YU Y M, RAINER B, AXEL V J. Morphological instability of heteroepitaxial growth on vicinal substrates:A phase-field crystal study[J]. Journal of Crystal Growth, 2011, 318(1): 18-22. DOI:10.1016/j.jcrysgro.2010.08.047 |
| [14] |
高英俊, 罗志荣, 黄礼琳, 等. 韧性材料的微裂纹扩展和连通的晶体相场模拟[J]. 中国有色金属学报, 2013, 23(7): 1892-1899. GAO Y J, LUO Z R, HUANG L L, et al. Phase-field-crystal modeling for microcrack propagation and connecting of ductile materials[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(7): 1892-1899. |
| [15] |
黄世叶, 李胜男, 胡绪志, 等. 晶界位错运动的空位晶体相场模拟[J]. 广西科学, 2016, 23(5): 459-464. HUANG S Y, LI S N, HU X Z, et al. Vacancy phase-field-crystal simulation of dislocation motion of grain boundary[J]. Guangxi Sciences, 2016, 23(5): 459-464. |
| [16] |
叶里, 黄礼琳, 孔令一, 等. 晶体弹性行为的晶体相场模拟[J]. 广西科学, 2016, 23(5): 474-477. YE L, HUANG L L, KONG L Y, et al. Phase-field-crystal simulation for elastic behavior of crystals[J]. Guangxi Sciences, 2016, 23(5): 474-477. |
| [17] |
叶里, 胡绪志, 黄礼琳, 等. 拉应力作用下晶界位错运动过程的晶体相场模拟[J]. 广西科学, 2016, 23(5): 470-473, 484. YE L, HU X Z, HUANG L L, et al. Phase-field-crystal simulation of grain boundary dislocation motion under tensile stress[J]. Guangxi Sciences, 2016, 23(5): 470-473, 484. |
| [18] |
WU K A, ADLAND A, KARMA A. Phase-field-crystal model for fcc ordering[J]. Physical Review E, 2010, 81(6): 061601. |
| [19] |
高英俊, 罗志荣, 黄创高. 晶体相场方法研究二维六角相向正方相结构转变[J]. 物理学报, 2013, 62(5): 050507. GAO Y J, LUO Z R, HUANG C G. Phase-field-crystal modeling for two-dimensional transformation from hexagonal to square structure[J]. Acta Physica Sinica, 2013, 62(5): 050507. |
| [20] |
毛鸿, 罗志荣, 黄世叶, 等. 材料裂纹扩展分叉机理的晶体相场法研究[J]. 广西科学, 2015, 22(5): 499-505. MAO H, LUO Z R, HUANG S Y, et al. Phase-field-crystal modeling for crack propagation and branch of materials[J]. Guangxi Sciences, 2015, 22(5): 499-505. |
| [21] |
高英俊, 罗志荣, 黄礼琳, 等. 变形合金的亚晶组织演化的相场模型[J]. 金属学报, 2012, 48(10): 1215-1222. GAO Y J, LUO Z R, HUANG L L, et al. Phase field model for microstructure evolution of subgrain in deformation alloy[J]. Acta Metallurgica Sinica, 2012, 48(10): 1215-1222. |
| [22] |
杨涛, 陈铮, 董卫平. 应力诱发双位错组亚晶界湮没的晶体相场模拟[J]. 金属学报, 2011, 47(10): 1301-1306. YANG T, CHEN Z, DONG W P. Phase field crystal simulation of stress-induced annihilation of sub-grain boundary with double-array dislocation[J]. Acta Metallurgica Sinica, 2011, 47(10): 1301-1306. |
| [23] |
任秀, 王锦程, 杨玉娟, 等. 纯物质晶界结构及运动的晶体相场法模拟[J]. 物理学报, 2010, 59(5): 3595-3600. REN X, WANG J C, YANG Y J, et al. Simulation of the structure and motion of grain boundary in pure substances by phase field crystal model[J]. Acta Physica Sinica, 2010, 59(5): 3595-3600. DOI:10.7498/aps.59.3595 |
| [24] |
刘瑶, 袁龙乐, 卢强华, 等. 晶体相场模拟取向角对晶界湮没过程的影响[J]. 广西科学, 2016, 23(5): 437-442. LIU Y, YUAN L L, LU Q H, et al. Phase-field-crystal simulation of effect of different orientation angle on annihilation of grain boundary[J]. Guangxi Sciences, 2016, 23(5): 437-442. |
 2017, Vol. 33
2017, Vol. 33 


