2. 玉林师范学院物理科学与工程技术系,广西玉林 537000
2. Institute of Physics Science and Engineering Technology, Yulin Normal University, Yulin, Guangxi, 537000, China
【研究意义】晶体材料通常由大量晶粒组成,取向不同的两晶粒间便会形成晶界[1-2]。按照两晶粒取向差的大小,晶界可大致分为小角度晶界和大角度晶界。小角度晶界的取向差小于10°,由一系列位错按特定方式排列而成。晶体中的位错引起晶体点阵结构发生畸变[2],但在稳定条件下,位错可以保持稳定结构。在外加应力的作用下,位错会发生运动,致使晶界(包括亚晶界)迁移,甚至是湮没[3-5]。因此,晶界的结构和迁移方式对晶体材料的加工具有重要影响[6],也是拓扑几何缺陷(空位、空洞、位错、晶界和微裂纹等)决定材料在介观和宏观尺度上的性能的一个重要例证[6]。然而,以目前的实验条件,很难实时观察晶体内部这些微结构的动态过程,但借助计算机模拟方法可以弥补这些实验上的不足。特别是近几年提出的晶体相场(PFC)方法[7-9],能够在扩散时间尺度(10-6s)上描述纳米尺度的原子运动,相对于分子动力学(MD)与传统相场方法[10-12]具有一定的优势。【前人研究进展】 PFC方法已得到广泛应用,例如可用于位错和晶界的迁移[13-14]、裂纹扩展[15-16]、结构相变[17-18]、晶界熔解[19-20]、小角度对称倾转亚晶界的湮没过程[21-23]和空位相互作用[24-26]等。【本研究切入点】 应用PFC方法模拟四晶粒的晶界位错运动和相互作用,分析位错的运动和自由能变化之间的内在联系,揭示位错运动、位错反应形式以及能量变化规律。【拟解决的关键问题】应用PFC方法模拟了取向差不同的条状晶形成对称和非对称亚晶界位错在外加应力作用下的运动、相互作用以及湮没的过程,同时从能量变化角度分析该过程的规律。
1 模型与方法原子密度场函数ρ(r)用相场变量表示,
| $ \rho \left( r \right)=\sum\limits_{n, m}{{{a}_{n, m}}{{e}^{iG\cdot r}}}+{{\rho }_{0}}, $ | (1) |
其中an, m代表Fourier系数,G代表倒格矢,r代表空间位置矢量。晶格原子的周期排列结构特征由∑anm所体现,ρ0代表原子平均密度。体系的自由能函数F表示为
| $ F=\int{\{\frac{\rho }{2}\left[\gamma +{{\left( 1+{{\nabla }^{2}} \right)}^{2}} \right]\rho +\frac{{{\rho }^{4}}}{4}\}\rm{d}\mathit{r}, } $ | (2) |
其中γ代表温度的参数。
Cahn-Hilliard动力学方程与时间相关,可以用来描述保守的原子密度场变量的演化,方程的表达式为
| $ \frac{\partial \rho }{\partial t}={{\nabla }^{2}}~\frac{\delta F}{\delta \rho }={{\nabla }^{2}}\left( \gamma \rho +{{\left( 1+{{\nabla }^{2}} \right)}^{2}}\rho +{{\rho }^{3}} \right)。$ | (3) |
对(3)式求解,得到稳定的三角相的二维单模近似解ρ为
| $ \begin{align} &\ \ \ \rho =A[\rm{cos}\left( \mathit{qx} \right)\rm{cos}\left( \mathit{qy}/\sqrt{3} \right)-\\ &\rm{cos}\left( 2\mathit{qy}/\sqrt{3} \right)/2]+{{\rho }_{0}}, \\ \end{align} $ | (4) |
其中,波矢
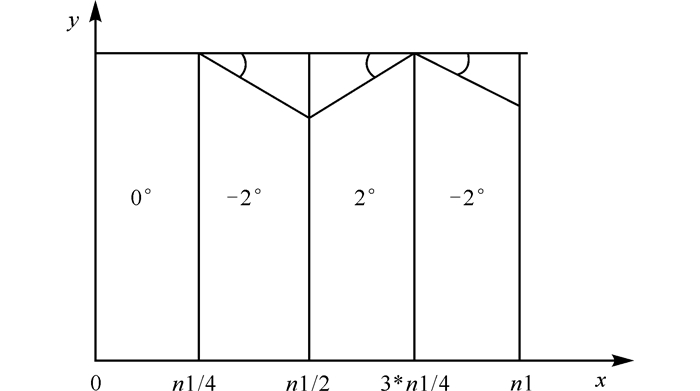
采用周期性边界条件进行模拟,选取空间步长为Δx=Δy=π/4,时间步长Δt=0.5。模拟参数γ=-0.25,ρ0=0.285。计算区域Lx×Ly=1024Δx×516Δy,设置成8个不同区域:4个晶粒区域,晶粒的初始取向角分别为0°,-2°, 2°,-2°,如图 1所示。样品经过105步弛豫,体系处于稳定状态。
|
图 1 晶粒初始化示意图 Fig.1 Schematic diagram of initial grains |
对样品施加应变。在二维条件下,变形采用等面积模型,即
| $ \mathit{\Delta x\Delta y}=\mathit{\Delta {x}'\Delta }{y}', $ | (5) |
式(5)中,Δx′和Δy′分别为变形后的空间步长,Δx和Δy分别为变形前的空间步长。设n为时间步数,Δt为时间步长,应变速率为
| $ \mathit{\Delta {x}'} =\left( 1+\varepsilon \right)\mathit{\Delta }x=\mathit{\Delta }x\left( 1+n\dot{\varepsilon }\mathit{\Delta }t \right), $ | (6) |
| $ \Delta {y}'=\mathit{\Delta }y/\left( 1+\varepsilon \right)=\mathit{\Delta }y/\left( 1+n\dot{\varepsilon }\mathit{\Delta }t \right)。$ | (7) |
在外应力的作用下,体系自由能曲线图像如图 2所示, 晶界位错的运动如图 3所示,图 3中a~m与图 2自由能曲线每一点对应。整个过程通过自由能曲线可细分为6个阶段,a~c为第1阶段,c~f为第2阶段,f~g为第3阶段,g~h为第4阶段,h~i为第5阶段,i~m为第6阶段。即自由能图像上的每一个极大值和极小值都对应一个阶段的终点和起点。弛豫后加力前的样品晶粒结构如图 3a所示,晶界能看到12个位错,分别用A~L表示。AB、CD、EFGH、IJKL这4列晶界中,同一列晶界的位错方向相同,而每一列都与相邻列的位错方向相反。加应变后,位错开始运动,AB和CD分别竖直向下和竖直向上作攀移运动,EFGH和IJKL也是如此,如图 3b所示。此时由自由能图像可知,在这一过程中,随着位错的攀移,能量不断增加,在积累到足够的能量后,即到了c点后,能量开始下降,位错也开始分解(图 3c)。

|
图 2 自由能曲线 Fig.2 Free energy curve |

|
图 3 体系演化过程 Fig.3 System evolution process |
由图 3d可知, 继续加力至24 000步,可以看到明显的位错分解图像,A分解为A1和A2,B分解为B1和B2,C~K位错也是如此,而位错L尚且没有完全分解,因为位错A未分解之前的运动方向为竖直向下,所以分解后的A1和A2朝着远离对方的方向运动,即竖直向下,即A1和A2分别沿着左下和右下运动;同理,位错B1和B2分别沿着左下和右下运动,位错C1、D1和C2、D2分别沿着左上和右上运动,图 3e即为运动过程的图像。随着应变的施加,位错A2和D1会相遇,由于两者的位错方向刚好相反,相遇后会产生湮没现象;同理,位错D2和F1也会产生湮灭现象,位错A1和J2也会湮没,此时晶粒的状态对应图 3f,能量也同时降低到极小值。此时,晶粒内还有3对相距比较近的位错:H2-I1、E2-J1、K1-F2,其中H2-I1和K1-F2这两对位错相距更近一些,E2-J1稍微远一点。
由图 3g可知,相距更近的位错对H2-I1和K1-F2相互吸引,最终湮没,而相距较远的位错对E2-J1仍然保持着原来的运动方向。此时,可以看到,图 2的自由能曲线图像再次出现了一个极小值g。至此,第4阶段结束。第5阶段g~h、第6阶段h~i(图 3g~i)所示)与第1阶段a~c、第2阶段c~f相似。在第5阶段中,剩余的位错随着应力的施加继续攀移,对应图 2能量也继续增加,当能量达到足够高时,位错就会摆脱晶界的束缚而产生滑移,最终两两相遇的位错发生湮灭现象。第6阶段完成后,整个体系只剩下2对位错,直到q点之前,这两对位错都没有发生湮没现象,只是一直在晶粒内运动。经过长时间的相向运动,它们最终还是在同一直线上相遇,至此,整个体系重新变成没有进行任何旋转变化的单晶。
根据以上分析,可以很好的理解图 2自由能曲线呈现波动式上升的变化。最初存在一个较高的峰,这是由于较多的位错攀移;较陡的下降,是因为较多的位错同时湮没。之后的峰谷波动就较为平缓,因为位错攀移和湮没的数量减少了。
4 结论位错的相互作用存在4种情况:二位错相向运动,若位错矢量方向完全相反且在同一直线上, 则相遇后发生湮没;如果运动方向不在一条直线上,但距离较近,则可以相互吸引,最后依然可以湮没;如果运动方向不在一条直线上,且距离较远,则无法相互吸引,只会朝着各自的运动方向继续运动;如果运动方向在一条直线上,但是位错方向不完全相同,它们相遇后不会湮没,而是组合形成一个复合位错。
| [1] |
徐恒均, 刘国勋. 材料科学基础[M]. 北京: 北京工业大学出版社, 2001. XU H J, LIU G X. Fundamentals of materals science[M]. Beijing: Beijing University of Technology Press, 2001. |
| [2] |
胡庚祥, 蔡珣, 戎咏华. 材料科学基础[M]. 3版. 上海: 上海交通大学出版社, 2010. HU G X, CAI X, RONG Y H. Fundamentals of materials science[M]. 3rd ed. Shanghai: Shanghai Jiaotong University Press, 2010. |
| [3] |
BOBYLEV S V, OVID'KO I A. Transformations of faceted grain boundaries in high-Tc superconductors[J]. Physical Review B, 2003, 67(13): 132506. DOI:10.1103/PhysRevB.67.132506 |
| [4] |
OVID'KO I A, SKIBA N V. Enhanced dislocation emission from grain boundaries in nanocrystalline materials[J]. Scripta Materialia, 2012, 67(1): 13-16. DOI:10.1016/j.scriptamat.2012.03.007 |
| [5] |
GUKKIN M Y, OVIDKO I A. Transformations of low-angle tilt boundaries in high-Tc superconductors[J]. Physical Review B, 2001, 63(6): 064515. DOI:10.1103/PhysRevB.63.064515 |
| [6] |
HAYAKAWA M, YAMAGUCHI K, KIMURA M. Visualization of subgrain structure for a ferritic 12Cr-2W steel using backscattered scanning electron microscopy[J]. Materials Letters, 2004, 58(21): 2565-2568. DOI:10.1016/j.matlet.2004.03.003 |
| [7] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70(5): 051605. DOI:10.1103/PhysRevE.70.051605 |
| [8] |
STEFANOVIC P, HAATAJA M, PROVATAS N. Phase field crystal study of deformation and plasticity in nanocrystalline materials[J]. Physical Review E, 2009, 80(4): 046107. DOI:10.1103/PhysRevE.80.046107 |
| [9] |
BERRY J, GRANT M, ELDER K R. Diffusive atomistic dynamics of edge dislocations in two dimensions[J]. Physical Review E, 2006, 73(1): 31609. |
| [10] |
WANG Y Z, LI J. Phase field modeling of defects and deformation[J]. Acta Materialia, 2010, 58(4): 1212-1235. DOI:10.1016/j.actamat.2009.10.041 |
| [11] |
YU Y M, BACKOFEN R, VOIGT A. Morphological instability of heteroepitaxial growth on vicinal substrates:A phase-field crystal study[J]. Journal of Crystal Growth, 2011, 318: 18-22. DOI:10.1016/j.jcrysgro.2010.08.047 |
| [12] |
ELDER K R, ROSSI G, KANERVA P, et al. Patterning of heteroepitaxial overlayers from Nano to micron scales[J]. Physical Review Letters, 2012, 108(22): 226102. DOI:10.1103/PhysRevLett.108.226102 |
| [13] |
GAO Y J, HUANG L L, DENG Q Q, et al. Phase field crystal simulation of dislocation configuration evolution in dynamic recovery in two dimensions[J]. Acta Materialia, 2016, 117: 238-251. DOI:10.1016/j.actamat.2016.06.021 |
| [14] |
罗志荣, 卢成健, 高英俊. 相场法研究初始微结构对晶粒长大的影响[J]. 广西科学, 2016, 23(5): 432-436, 442. LUO Z R, LU C J, GAO Y J. Phase field study on effect of initial microstructure on grain growth[J]. Guangxi Sciences, 2016, 23(5): 432-436, 442. |
| [15] |
黄礼琳, 叶里, 胡绪志, 等. 不同晶向取向的裂纹扩展演化模拟[J]. 广西科学, 2016, 23(5): 454-458, 469. HUANG L L, YE L, HU X Z, et al. Simulation study of crack propagation and evolution in different crystal orientations[J]. Guangxi Sciences, 2016, 23(5): 454-458, 469. |
| [16] |
温振川, 宁岁婷, 张睿, 等. 纳米级缺口起裂临界条件的晶体相场模拟[J]. 广西科学, 2016, 23(5): 448-453. WEN Z C, NING S T, ZHANG R, et al. Phase-field-crystal simulation of critical conditions for the crack initiation of nanoscale notch[J]. Guangxi Sciences, 2016, 23(5): 448-453. |
| [17] |
CHEN L Q. Phase-field method of phase transitions/domain structures in ferroelectric thin films:A review[J]. Journal of the American Ceramic Society, 2008, 91(6): 1835-1844. DOI:10.1111/j.1551-2916.2008.02413.x |
| [18] |
GREENWOOD M, ROTTLER J, PROVATAS N. Phase-field-crystal methodology for modeling of structural transformations[J]. Physical Review E, 2011, 83(3): 031601. |
| [19] |
MELLENTHIN J, KARMA A, PLAPP M. Phase-field crystal study of grain-boundary premelting[J]. Physical Review B, 2008, 78(18): 184110. DOI:10.1103/PhysRevB.78.184110 |
| [20] |
高英俊, 黄礼琳, 周文权, 等. 高温应变下的亚晶界湮没与位错旋转机制的晶体相场模拟[J]. 中国科学:技术科学, 2015, 45(3): 306-321. GAO Y J, HUANG L L, ZHOU W Q, et al. Phase field crystal simulation of subgrain boundary annihilation and dislocation rotation mechanism under strain at high temperature[J]. Scientia Sinica:Technologica, 2015, 45(3): 306-321. |
| [21] |
高英俊, 袁龙乐, 刘瑶, 等. 不同温度晶界位错湮没过程的晶体相场模拟[J]. 广西科学, 2014, 21(3): 203-208. GAO Y J, YUAN L L, LIU Y, et al. Phase field crystal simulation of dislocation annihilation at different temperature[J]. Guangxi Sciences, 2014, 21(3): 203-208. |
| [22] |
刘瑶, 袁龙乐, 卢强华, 等. 晶体相场模拟取向角对晶界湮没过程的影响[J]. 广西科学, 2016, 23(5): 437-442. LIU Y, YUAN L L, LU Q H, et al. Phase-field-crystal simulation of effect of different orientation angle on annihilation of grain boundary[J]. Guangxi Sciences, 2016, 23(5): 437-442. |
| [23] |
杨瑞琳, 刘瑶, 胡绪志, 等. 双位错滑移运动的晶体相场模拟[J]. 广西科学, 2016, 23(5): 443-447. YANG R L, LIU Y, HU X Z, et al. Phase-field-crystal simulation of double dislocation Gli-ding[J]. Guangxi Sciences, 2016, 23(5): 443-447. |
| [24] |
黄世叶, 李胜男, 胡绪志, 等. 晶界位错运动的空位晶体相场模拟[J]. 广西科学, 2016, 23(5): 459-464. HUANG S Y, LI S N, HU X Z, et al. Vacancy phase-field-crystal simulation of dislocation motion of grain boundary[J]. Guangxi Sciences, 2016, 23(5): 459-464. |
| [25] |
叶里, 胡绪志, 黄礼琳, 等. 拉应力作用下晶界位错运动过程的晶体相场模拟[J]. 广西科学, 2016, 23(5): 470-473, 484. YE L, HU X Z, HUANG L L, et al. Phase-field-crystal simulation of grain boundary dislo-canon motion under tensile stress[J]. Guangxi Sciences, 2016, 23(5): 470-473, 484. |
| [26] |
叶里, 黄礼琳, 孔令一, 等. 晶体弹性行为的晶体相场模拟[J]. 广西科学, 2016, 23(5): 474-477. YE L, HUANG L L, KONG L Y, et al. Phase-field-crystal simulation for elastic behavior of crystals[J]. Guangxi Sciences, 2016, 23(5): 474-477. |
 2017, Vol. 33
2017, Vol. 33 


