【研究意义】医保欺诈成为当前医保领域的一个难题。医保数据具有保险类数据的特征,数据量大、数据属性类型多、动态性强,且包括众多的数据以及庞大而复杂的属性关系。大数据背景下,运用相关聚类算法主动挖掘医疗保险欺诈行为,显得尤其重要。【前人研究进展】当前研究大多采用神经网络等有监督的学习方法或者未赋予指标权重,主观性较强。比如王熙照等[1]根据模糊等价关系将给定对象划分成一些等价类,在一定程度上会导致划分不精确等问题。【本研究切入点 】在经典的聚类分析算法中,无论是采用欧氏距离还是马氏距离,都未将所有指标赋予各自的权重。本研究就医保欺诈行为的主动发现这一问题进行探讨,并采用非辅助学习 (无监督学习) 方法。通过比较分析,采用聚类分析算法,对数据进行分类处理,认为出现的孤立点为疑似欺诈点。【拟解决的关键问题】本研究将先构造交叉熵函数,再通过粒子群优化算法不断更新属性权重,得到最终满足交叉熵函数CFuzziness (ω) 的条件。另外,为提高FCM聚类算法的速度,将通过聚类有效性评价来估计聚类个数,最后将属性权重以及聚类个数应用于经典FCM聚类算法进行聚类分析。
1 基于PSO的加权FCM算法传统聚类方法忽略各因素的权重差异,因此本研究引入交叉熵函数CFuzziness (ω),该函数刻画随着权重ω的改变,分类模糊程度的变化。通过调整ω的值,使分类的模糊程度尽量小。ω的最优解使同一类的点尽量靠近,不同类的点尽量远离,即ω应对应于CFuzziness (ω) 取最小值时的最优解。常用的梯度下降算法[1]的时间复杂度大,且容易陷入局部最优解,因此本研究采用粒子群优化算法[2]求解ω的最优解。另外,运用聚类有效性评价[3]中的CH有效性指标[4]来确定最佳聚类数,然后再根据聚类数来进行下一步的FCM聚类算法[5]。
1.1 符号定义相关的符号含义如表 1所示。
| 表 1 符号说明表 Table 1 Symbol description |
引入基于属性权重的欧氏距离dpq(ω),称之为改进的欧氏距离,其定义为
| $ d_{pq}^{\left( \omega \right)} = \sqrt {\sum\limits_{k = 1}^m {{\omega _k}{{\left( {{X_{pk}}-{X_{qk}}} \right)}^2}} }, $ | (1) |
其中ω={ω1, ω2, …, ωm}是权重向量,对应于属性向量;ωk∈[0, 1]为第k维属性对应的权重,在相似性度量中,第k维属性的作用与ωk的成正比,则类间距离可定义为
| $ d\left( {s, t} \right) = \frac{1}{{{n_s}{n_t}}}\sum\limits_{i = 1}^{{n_s}} {\sum\limits_{j = 1}^{{n_t}} {d_{{X_{si}}{X_{tj}}}^{\left( \omega \right)}} } 。$ | (2) |
为得到属性权重ωk,引入交叉熵函数CFuzziness (ω)[1],采用改进的欧氏距离dpq(ω)作为度量指标后,在相似性关系不变 (即如果Spq>0.5,则Spq(ω)>0.5;如果Spq < 0.5,则Spq(ω) < 0.5) 的前提下,相似性度量定义也相应变化,表示为
| $ S_{pq}^{\left( \omega \right)} = \frac{1}{{1 + \beta \times d_{pq}^{\left( \omega \right)}}}。$ | (3) |
常数β∈[0, 1],β值通过调整,使得Spq(ω)能够近似于正态分布散落在[0, 1]内。由下式得到β的近似值[1]:
| $ \frac{2}{{n\left( {n-1} \right)}}\sum\limits_{q < p} {{S_{pq}} = \frac{2}{{n\left( {n-1} \right)}}} \sum\limits_{q < p} {\frac{1}{{1 + \beta \times {d_{pq}}}}} = $ | (4) |
为让聚类结果具有模糊性相对较小的性质,通过调整数据集各属性权重,使得相似数据间的距离更小,而不相似数据间的距离更大,即通过综合函数来评价各个点之间在各属性作用下的相似程度,使总体范围内的模糊性最小。基于以上分析,引进交叉熵函数[1]:
| $ \begin{array}{l} \;\;\;\;\;\;{\rm{CFuzziness}}\left( \omega \right) = \frac{{-2}}{{n\left( {n-1} \right)}}\sum\limits_{q < p} {\frac{1}{2}} \left( {S_{pq}^{\left( \omega \right)} \times } \right.\\ \left. {\log {S_{pq}} + \left( {1-S_{pq}^{\left( \omega \right)}} \right) \times \log \left( {1 - {S_{pq}}} \right)} \right)。\end{array} $ | (5) |
本研究利用粒子群优化算法[6]来极小化交叉熵CFuzziness (ω)。假设目标搜索空间是一个D维数据集,PSO算法初始化为一个群落,这个群落由N个粒子组成,其中第i个粒子用一个D维的向量Xi={xi1, xi2, …, xiD}, i=1, 2, …, N来表示,也用一个D维的向量描述第i个粒子“飞行”的速度,记作:
| $ {V_i} = \left\{ {{v_{i1}}, {v_{i2}}, \cdots, {v_{iD}}} \right\}, i = 1, 2, \cdots, N, $ | (6) |
迄今为止第i个粒子搜索到的最佳位置称为个体极值,记作:
| $ {P_{best}} = \left\{ {{p_{i1}}, {p_{i2}}, \cdots, {p_{iD}}} \right\}, i = 1, 2, \cdots, N, $ | (7) |
迄今为止整个粒子群搜索到的最佳位置为全局极值,记作:
| $ {g_{best}} = \left\{ {{p_{g1}}, {p_{g2}}, \cdots, {p_{gD}}} \right\}, g = 1, 2, \cdots, D。$ | (8) |
粒子在飞行时不断地根据公式 (9) 和 (10) 来决策,并通过下面两个公式[7]来更新位置xid和速度Vid:
| $ {V_{id}} = w \times {v_{id}} + {c_1}{r_1}\left( {{p_{id}}-{x_{id}}} \right) + {c_2}{r_2}\left( {{p_{gd}}-{x_{id}}} \right), $ | (9) |
| $ {x_{id}} = {x_{id}} + {v_{id}}, i = 1, 2, \cdots, N, g = 1, 2, \cdots, D。$ | (10) |
粒子群优化算法优化属性权重ω值的流程[8]如下:
1) 初始化粒子群中的群体规模N,各粒子速度Vi和粒子位置Xi;
2) 通过∑ViXi计算得到各粒子的适应度值,即目标函数值Fi t[i];
3) 比较各粒子的适应度值Fi t[i]与个体极值Pbest(i),若Fi t[i]>Pbest(i),则Fi t[i]取代Pbest(i);
4) 比较各粒子的适应度值Fi t[i]与全局极值gbest,若Fi t[i]>gbest(i),则用Fi t[i]取代gbest;
5) 根据公式 (9) 和 (10) 更新粒子的速度Vi和位置Xi;
6) 满足最大循环次数或最小误差时退出循环,否则返回步骤2)。
1.4 聚类有效性评价通常,在聚类之前需要划分聚类数,而对于数据集划分的类数往往是未知的,也不容易得到。聚类有效性评价就是通过选定聚类有效性指标[9]来评价聚类算法和聚类个数的优劣,使得聚类有效性指标最优时的聚类个数为最佳聚类个数。本研究选取Calinski-Harabasz (CH) 有效性指标[3]来进行评价。
对于m维数据集X={X1,X2, …, Xn}, n为数据集中数据对象个数,其中Xi={x1, x2, …, xm}表示第i个数据对象。划分式聚类算法[10]将数据集X分为NC个子集X={C1, C2, …, CNC},Ci为X的簇 (子类),用c表示数据集X的中心点,ci表示簇Ci的中心点,ni表示簇Ci中的数据对象的个数,d(Xi, Xj) 表示数据对象i和数据对象j之间的距离。
于是CH有效性指标的定义如下[11]:
| $ {\rm{CH}}\left( {NC} \right) = \frac{{\frac{1}{{NC-1}}\sum\limits_{i = 1}^{NC} {{n_i}{d^2}\left( {{c_i}, c} \right)} }}{{\frac{1}{{n-NC}}\sum\limits_{i = 1}^{NC} {\sum\limits_{x \in {c_i}} {{d^2}\left( {x, {c_i}} \right)} } }}. $ | (11) |
采用估计聚类个数工具箱 (NCT)[11]进行聚类有效性评价,NCT包括4个外部有效性指标和8种内部有效性指标。主文件设计为如何使用聚类算法、有效性指标和方法来估计聚类个数。
1.5 加权模糊C-均值 (WFCM)K-Means[12]隶属度取值为0或者1,根据“类内误差的平方和最小”这个准则不断迭代。设X={X1, X2, …, Xn}⊂RP,RP表示p维的向量空间,NC表示聚类数,隶属度μij表示第j个数据样本从属于第i类的程度,目标函数为
| $ \left( {\min } \right){J_1} = \sum\limits_{i = 1}^{NC} {\sum\limits_{j = 1}^N {{\mu _{ij}}{{\left\| {{x_j}-{v_i}} \right\|}^2}} } 。$ | (12) |
K-Means算法简单快速,时间复杂度为O (nKτ),呈线性关系,因此对于大数据特别是数值型大数据的处理比较有效,但是K-means也有以下3个方面的缺点:
①对于初始聚类中心有很强的敏感性以及依赖性;
②K的选取需要一定的先验知识;
③不适用于数据分布呈凸形状的聚类,对孤立点很敏感。
典型K-Means聚类算的基本根据是“类内加权误差平方和最小化”[13],其目标函数为
| $ \left( {\min } \right){J_2} = \sum\limits_{i = 1}^{NC} {\sum\limits_{k = 1}^N {\mu _{ik}^2{{\left\| {{x_k}-{v_i}} \right\|}^2}} } 。$ | (13) |
Bezdek对于上一目标函数推广到更为普遍的形式:
| $ \left( {\min } \right){J_m} = \sum\limits_{i = 1}^{NC} {\sum\limits_{k = 1}^N {\mu _{ik}^m{{\left\| {{x_k}-{v_i}} \right\|}^2}} } . $ | (14) |
建立在FCM算法的基础上,李伯年[14]将FCM算法里的欧式距离进行优化,推广到广义的欧式距离,即加权模糊C-均值聚类算法 (WFCM),适用于大数据的排序与聚类。WFCM算法的基本步骤类似于FCM算法步骤,只是在目标函数上存在区别以及更新隶属度矩阵要考虑属性的权重。
WFCM的目标函数为
| $ \begin{array}{l} \left( {\min } \right){J_m} = \sum\limits_{i = 1}^{NC} {\sum\limits_{k = 1}^N {\mu _{ik}^m{\omega _l}{{\left\| {{x_k}-{v_i}} \right\|}^2}} }, l = 1, \cdots, \\ m, \left( {m为数据的维数} \right)。\end{array} $ | (15) |
WFCM算法的具体步骤如下:
1) 声明聚类的簇的个数NC,取值范围为[2, n],n为数据个数,给定停止迭代的阈值ε以及初始的聚类中心V0、迭代累计数b=0,另外数据维数m的取值为2;
2) 初始隶属度矩阵U0=[uij(0)]根据先验知识确定,并用下列公式计算及更新隶属度矩阵Ub=[uij]:
| $ u_{ij}^{\left( {b + 1} \right)} = {\left[{\sum\limits_{k = 1}^{NC} {{{\left( {\frac{{{{\left( {d_{ij}^{\left( \omega \right)}} \right)}^2}}}{{{{\left( {d_{kj}^{\left( \omega \right)}} \right)}^2}}}} \right)}^{\frac{1}{{m-1}}}}} } \right]^{ -1}}, 1 \le i \le NC, 1 \le j \le n。$ | (16) |
其中dij(ω)=
3) 用下列公式修正聚类中心Vb+1:
| $ v_i^{\left( {b + 1} \right)} = \frac{{\sum\limits_{j = 1}^n {\left( {u_{ij}^{\left( b \right)}} \right){m_{{x_j}}}} }}{{\sum\limits_{j = 1}^n {\left( {u_{ij}^{\left( b \right)}} \right)m} }}, 1 \le i \le NC; $ | (17) |
4) 如果‖Vb-Vb+1‖≤ε,停止算法并输出隶属度矩阵U以及聚类中心V,否则令b=b+1,并回到步骤2) 继续执行。停止迭代以后,若max (uij)=ukj,则xj∈第k类。
2 医保欺诈行为主动发现中的应用 2.1 数据分析及预处理医保数据是深圳医院一个月30多万条记录的数据,具有庞大而复杂的属性关系,且含有众多缺失或属性不清晰的数据。因此,先进行数据预处理。定性定量地从病人、医生、科室的角度进行分析:从病人的角度,包括一张卡一定时间内反复多次拿药、单张账单费用较高、一人持多卡即一卡多用这3种情况。再结合疑似欺诈账单号,从医生的角度和科室的角度来进行分析,重点是从病人的角度来分析。
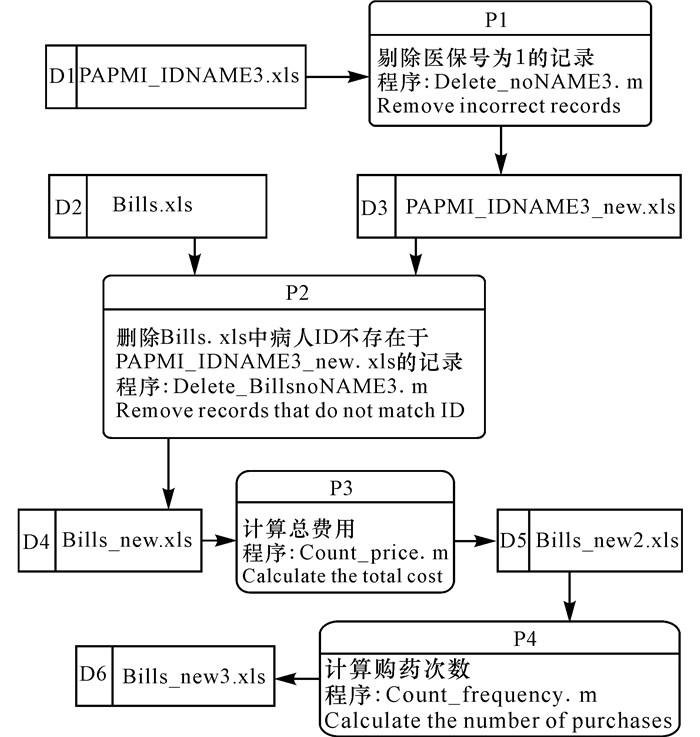
经过数据准备阶段以后,得到两个新表PAPMI_IDNAME3和Bills。首先,用Delete_noNAME3去处理表PAPMI_IDNAME3,生成不含有医保号为1的表PAPMI_IDNAME3_new。其次,根据PAPMI_IDNAME3_new删除Bills中病人ID不存在于PAPMI_IDNAME3_new的记录,用Delete_BillsnoNAME3去实现。再次,因为账单Bills_new中同一个账单号可以有多条记录,所以应将同一个账单号的多条记录叠加一起。观察数据,知道表中除第3列 (总价) 的数据不同,其余都相同,依次对第3列的数据相加后为总费用,仍存储于第3列,使用函数Count_price处理后生成数据表Bills_new2。最后,运用函数Count_frequency统计每个病人ID购药的次数,生成表Bills_new3,其新增的第6列为统计出来的每个病人ID购药的次数。
为方便直观地了解本阶段的处理过程,用Visio绘制数据流模型图如图 1所示。
|
图 1 数据预处理阶段数据流模型 Fig.1 Data flow model of the data preprocessing stage |
经过数据预处理阶段后,生成包括59 081条数据记录的表Bills_new3,其6列数据分别是执行科室、病人ID、总费用、下医嘱医生ID、账单号、购药次数。为了采用粒子群优化算法求解权重ω的最优解,主函数Calcu_weight调用6个M文件,分别为PSOstep.m、CFBeta.m、Gwank.m、ISwarm.m、PProcess.m、standard.m。
主函数Calcu_weight为
>>bills=xlsread (‘Bills_new3.xls’);
>>DATA=bills (1:10000, :);
>>DATA=standard (DATA);
>>DIS=pdist (DATA);
>>DDIS=squareform (DIS);
>>Scope=[0, 1;0, 1;0, 1;0, 1;0, 1];
>>w=PProcess (30, 5, Scope, @ISwarm, @PSOstep, @Gwank, 0, 0, 1000);
基于以上程序,得到各项属性的权重如表 2所示。
| 表 2 各属性权重表 Table 2 Attribute weight |
因为估计聚类个数工具箱 (NCT) 的使用中,利用zeros (n, n) 创建高维数据,但是由于内存溢出的限制,必须对Bills_new3拆分后运算,然后依次对它们运行NCT估计聚类个数。
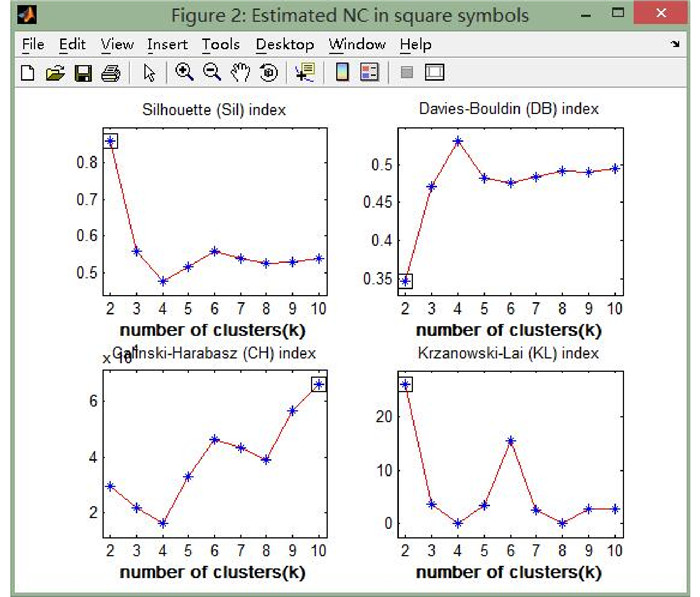
估计聚类个数工具箱 (NCT)[13]包括4个外部有效性指标和8种内部有效性指标,其中包括Calinski-Harabasz (CH) 有效性指标[4],本研究仅利用NCT中的CH指标。通过MATLAB对data1使用NCT估计聚类个数的部分输出结果如图 2所示。
|
图 2 MATLAB使用NCT估计聚类个数输出结果 Fig.2 The NCT estimated number of cluster outputs by MATLAB |
观察可知,CH有效性指标显示当聚类个数为10时,CH值最大,即类的自身紧密,类与类之间分散,即更优的聚类结果。同理,再依次对data2, …, data10的数据进行聚类有效性评价,c为最佳聚类数。结果 (省略小数) 整理如表 3所示。
| 表 3 全部data的估计聚类个数结果 Table 3 The estimated number of clustering results for all data |
基于数据表Bills_new3、属性权重ω以及最佳聚类个数c,对数据表运用加权模糊C-均值聚类方法进行聚类,编写4个M文件:WFCMClust.m、distwfcm.m、stepwfcm.m、initwfcm.m,其中主函数WFCMClust.m分别调用其它两个函数。4个M文件的作用分别如下:
①WFCMClust.m:采用加权模糊C-均值对数据集data聚为cluster_n类;
②distwfcm.m:循环计算得所有数据点与每一个聚类中心的距离;
③stepwfcm.m:迭代计算出新的隶属度矩阵、目标函数值以及新的聚类中心;
④initwfcm.m:初始化隶属度函数矩阵。
将结果隶属度矩阵U提取出来并整理成表WFCM_data1.xls,部分数据如表 4所示。其中,表的行代表数据记录,列代表聚类后的簇编号,每一行中最大的目标函数值所在的列即为该数据行所归属的类。
| 表 4 WFCM算法输出的隶属度矩阵 Table 4 The membership matrix of WFCM algorithm output |
对WFCM_data1进行聚类分析,目的是根据隶属度矩阵进行聚类划分,划分的原则是每一行中最大的目标函数值所在的列即为该数据行所归属的类,代码如下:
>>data=xlsread (‘WFCM_data1’);
>>[max_data, index]=max (data, [], 2);
>>plot (index, ‘*’); %绘制散点图分布,目的是大体上观察聚类效果
>>Bills_new3=xlsread (‘Bills_new3’); %录入原始数据
>>Bills_new3=[Bills_new3, index]; %将簇编号添加到最后一列,即第7列
>>sortrows (Bills_new3, 7);%将表Bills_new3按第7列排序,方便选出疑似欺诈记录
>>xlswrite (‘Result’, Bills_new3);
运行以上程序后,输出结果为Result.xls,其中第7列已经排序。
3 实例分析根据之前的假设,医保欺诈行为不存在模仿与学习,呈孤立点状分布,即不涉及医保欺诈的账单记录归在一类中,而其他涉嫌医保欺诈的账单记录则归在其他类里。类似于以上data1的处理过程,对data2~data10的数据用WFCM算法以及聚类分析后,整理成169条记录的result.xls,部分记录见表 5。
| 表 5 根据隶属度矩阵进行聚类分析的输出结果 Table 5 The result of clustering analysis according to membership matrix |
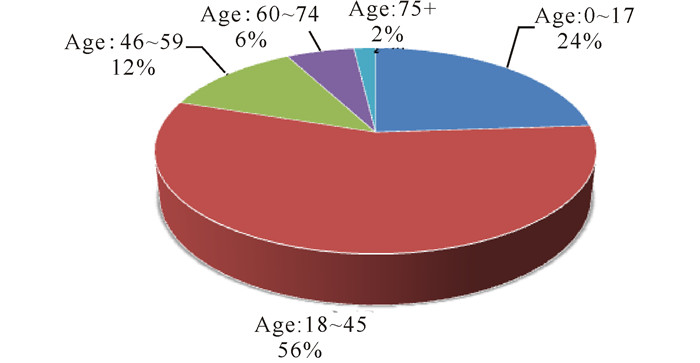
本研究的数据是2014年1月1日至2014年1月31日深圳市全部医院的医疗保险数据,年龄这一属性应该列入定量的标准中。利用病人资料的身份证号码变成计算年龄,绘出各个年龄阶段所占比例的情况 (图 3)。
|
图 3 各年龄阶段所占比例 Fig.3 The pie chart of the age |
从一定程度上考虑,即使有监护人,年龄太小或者年龄太老的病人涉嫌医保欺诈的可能性都很小,因此编写M函数deal_age.m为169条记录的result.xls添加年龄,并删除0~17岁及75岁以上病人的记录,最终输出127条嫌疑记录,部分结果见表 6。
| 表 6 聚类分析最终结果——疑似医保欺诈记录 Table 6 Clustering analysis results-suspected medical insurance fraud records |
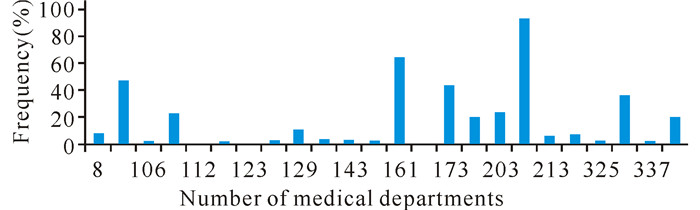
医生和科室也可能是医保欺诈问题的对象,因此应从科室的角度和医生的角度来发现医保欺诈记录。涉嫌医保欺诈科室通常为下医嘱科室,因此本研究重点分析下医嘱科室信息,考虑到某些科室需要长期接待同一病人或者属于高频次使用的科室,所以还需利用疑似账单号筛选出与之相关的科室,并统计出与这些疑似医保欺诈的账单号关联的次数来确定嫌疑科室。用delete_unsuspected.m删除账单号不存在于疑似欺诈账单号Suspected中的相关记录,然后重新通过数据透视图对所有科室绘制柱形图,如图 4所示。
|
图 4 关联可疑账单号后的下医嘱科室交易频次 Fig.4 The frequency column chart of medical advice department associated with the suspicious bill number |
从图 4中可以看出,某些科室的交易频次相对差别存在较大差异,频次较高的科室可作为重点排查和整治的目标,这才能准确地划分出的嫌疑科室。
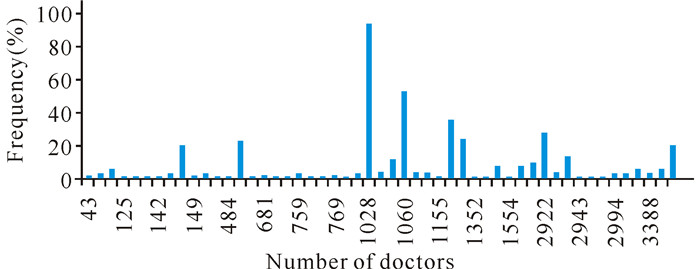
同样利用delete_unsuspected.m处理的结果,通过数据透视图对所有科室绘制柱形图,频次较高的医生可作为重点排查和整治的目标,这才能准确地划分出嫌疑医生,并以此作为划分嫌疑医生的标准 (图 5)。
|
图 5 关联可疑账单号后的医生交易频次 Fig.5 The frequency column chart of doctor associated with the suspicious bill number |
研究表明,将PSO算法优化的权重应用于WFCM聚类算法与聚类有效性评价,用聚类有效性评价估计最佳聚类数代替人工对聚类数的经验取值,既提高了聚类算法的高效性,又避免了主观评价对分类的影响。将研究结果应用于30万条医保欺诈数据的主动发现,得出疑似医保欺诈的127条记录。然而在研究的过程由于技术和篇幅的有限,也由于本文所提供的数据有限性和属性粗糙性,还有大量的未完成的探索性及尝试性的工作没有体现在论文中,但是对于此课题的探索和研究依然没有终止。
| [1] |
王熙照, 王丽娟, 王利伟. 传递闭包聚类中的模糊性分析[J]. 计算机工程与应用, 2003, 39(18): 92-94. WANG X Z, WANG L J, WANG L W. The fuzziness analysis of transitive closure clustering[J]. Computer Engineering and Applications, 2003, 39(18): 92-94. |
| [2] |
李宁. 粒子群优化算法的理论分析与应用研究[D]. 武汉: 华中科技大学, 2006. LI N.Analysis and application of particle swarm optimization[D].Wuhan:Huazhong University of Science and Technology, 2006. http://www.oalib.com/references/17399220 |
| [3] |
BEZDEK J C. Cluster validity with fuzzy sets[J]. Journal of Cybernetics, 1974, 3(3): 58-73. |
| [4] |
CALIЍSKI T, HARABASZ J. A dendrite method for cluster analysis[J]. Communications in Statistics, 1974, 3(1): 1-27. |
| [5] |
李明华, 刘全, 刘忠, 等. 数据挖掘中聚类算法的新发展[J]. 计算机应用研究, 2008, 25(1): 13-17. LI M H, LIU Q, LIU Z, et al. New developments of clustering methods in data mining[J]. Application Research of Computers, 2008, 25(1): 13-17. |
| [6] |
王纵虎, 刘志镜, 陈东辉. 基于粒子群优化的模糊C-均值聚类算法研究[J]. 计算机科学, 2012, 39(9): 166-169. WANG Z H, LIU Z J, CHEN D H. Research of PSO-based fuzzy C-means clustering algorithm[J]. Computer Science, 2012, 39(9): 166-169. |
| [7] |
武妍, 徐敏. 一种改进的粒子群优化算法[J]. 计算机工程与应用, 2006, 42(33): 40-42. WU Y, XU M. Modified particle swarm optimization algorithm[J]. Computer Engineering and Applications, 2006, 42(33): 40-42. |
| [8] |
刘逸. 粒子群优化算法的改进及应用研究[D]. 西安: 西安电子科技大学, 2012. LIU Y.Improvements and applications of particle swarm optimization algorithm[D].Xi'an:Xidian University, 2012. |
| [9] |
刘燕驰, 高学东, 国宏伟, 等. 聚类有效性的组合评价方法[J]. 计算机工程与应用, 2011, 47(19): 15-17. LIU Y C, GAO X D, GUO H W, et al. Ensembling clustering validation indices[J]. Computer Engineering and Applications, 2011, 47(19): 15-17. |
| [10] |
孙吉贵, 刘杰, 赵连宇. 聚类算法研究[J]. 软件学报, 2008, 19(1): 48-61. SUN J G, LIU J, ZHAO L Y. Clustering algorithms research[J]. Journal of Software, 2008, 19(1): 48-61. |
| [11] |
WANG K J.(Simple) Tool for estimating the number of clusters[EB/OL].2016-04-10, http://www.mathworks.com/matlabcentral/fileexchange/13916.
|
| [12] |
SULAIMAN S N, ISA N A M. Adaptive fuzzy-K-means clustering algorithm for image segmentation[J]. IEEE Transaction on Consumer Electronics, 2010, 56(14): 2661-2668. |
| [13] |
DUNN J C. Well-separated clusters and the optimal fuzzy partitions[J]. Journal of Cybernetics, 1974, 4(1): 95-104. |
| [14] |
李柏年. 加权模糊C-均值聚类[J]. 模糊系统与数学, 2007, 21(1): 106-110. LI B N. Weigh on cluster fuzzy C-mean[J]. Fuzzy Systems and Mathematics, 2007, 21(1): 106-110. |
 2017, Vol. 33
2017, Vol. 33 

