【研究意义】图是一种用来描述事物之间特定关系的重要数学模型和数据结构,广泛应用于生活中的各个领域,例如万维网、社交网络、蛋白质交互网络、化学分子结构等[1]。随着图数据规模的不断增大,对其进行有效和快速的分析和处理仍然面临着严峻的挑战,而图模式匹配技术 (Graph Pattern Matching) 作为实现图数据上高效查询的重要方法,已成为国内外学者的研究热点。【前人研究进展】从匹配结果与模式图是否完全一致的角度看,图匹配问题可以分为精确匹配和非精确匹配,其中,精确匹配一般通过定义图同构和子图同构来分析数据图和模式图之间的关系;非精确图匹配一般通过定义编辑距离、最小公共超图和最大公共子图来衡量两个图之间的相似程度[1]。研究者对最大公共子图问题进行了大量的研究,1973年,Levi[2]描述了一种求解最大公共子图的方法;1982年,Mcgregor[3]提出最大公共子图的回溯搜索算法;2004年,Krissinel等[4]针对公共子图同构,提出一种有更好搜索策略的基于回溯的树搜索算法;2005年,Suters等[5]提出一种基于最大团问题的“团分支”算法;2007年,Abu-khzam等[6]提出带有回溯策略的顶点覆盖和最大独立集相结合的技术;2016年,Nirmala等[7]在顶点覆盖的基础上提出二元搜索树的算法,能够更快地求解基于点的最大公共子图;2011年,Ndiaye等[8]首次提出结合约束满足问题 (CSP) 的求解思想,建立最大公共子图的软约束模型,利用约束传播等方法对模型进行求解,后来Minot等[9]在这种软约束模型的基础上,利用相容图和独立子图的思想完成最大公共子图的求解。Ndiaye等[8]和Minot等[9]证明引入约束满足问题模型可以清晰的刻画两个图的信息以及对应关系,改善了最大公共子图的求解效率。约束满足问题是人工智能领域的一个重要研究课题,它在复杂调度、资源分配、优化排序、模式识别与规划等领域都有广泛的应用[10]。其目标是寻找能满足所有约束条件的解,然而,在求解经典约束满足问题时,会因为约束限制过于严格而使得整个问题无解,所以,为了满足实际需要,研究者对经典CSP进行了拓展,提出了软约束满足问题 (Soft SCP),将CSP的求解目标转化为对Soft CSP求解。Soft CSP是在经典CSP的基础上,给CSP中的每个约束附加一个权值,该权值表示约束的优先级、满足程度等,通过放松一些约束条件,就可能找到问题的最优解,弥补了经典CSP的不足[11]。【本研究切入点】在Soft CSP中引入代数决策图 (ADD) 技术,可以用于求解最大公共子图。【拟解决的关键问题】在Ndiaye等[8]和Minot等[9]提出的软约束模型基础上,引入了符号ADD求解方法,并结合深度优先分支定界算法,实现对最大公共子图问题的求解。
1 预备知识 1.1 软约束满足问题软约束满足问题一般可以定义为一个四元组〈X, D, C, λ〉,其中:
(1)X={x1, x2, …, xn}为n个变量的有限集;
(2)D={D(x1), D(x2), …, D(xn)}为n个变量的值域集合;Di为变量Xi的值域,i={1, 2, …, n};
(3)C={c1, c2, …, cm}为约束关系集,ci(xi1, xi2, …, xij)⊆D(xi1)×D(xi2)×…×D(xij),i=1, 2, …, m, 1≤j≤n,vij∈X(l=1, 2, …, j),Dij为变量xij的域,称xi为定义在变量集{xi1, xi2, …, xij}⊆X上的j元约束。若C所有的约束均为一元或者二元约束,则称该Soft CSP为二元Soft CSP。本文仅讨论二元Soft CSP,对于二元CSP中的一组变量{x1, x2, …, xn}的一个完全赋值。
λ表示在匹配过程中不匹配节点所产生的代价值,这里指不匹配的节点个数。若二元Soft CSP中的一组变量{x1, x2, …, xi}⊆X,t= < v1, v2, …, vi>∈D(x1)×D(x2)×…×D(xi), 1≤i≤n, 其中vi为变量xi的取值。当t=n时,称赋值t是Soft CSP的一个完全实例化,否则为部分实例化,将总约束代价值表示为cost (t),则有约束的约束值表示cost (t)=λ。Soft CSP求解的目标是找到变量集X的一种完全实例化t,从而使得cost (t) 最小。
1.2 代数决策图 (ADD)有序二叉决策图 (OBDD) 是布尔函数的一种有效图形和数学描述技术[12-13]。在OBDD的基础上,Bahar等[14]通过引入多个非布尔终节点,将OBDD的布尔域扩展到有限域,给出了ADD的相关定义和基本操作,极大地改善了伪布尔函数和有限域取值函数的描述能力。
定义1.1 任意一个自变量取值只能是0或1,函数值可为实数的n元函数,称为n元伪布尔函数。如果实数集为R,B={0, 1},那么n元伪布尔函数可以表示为f:Bn→R。
定义1.2 对于从{0, 1}n到S的伪布尔函数f(x1, x2, …, xn),它的伪布尔函数族是指在布尔变量x1, x2, …, xn的不同输入模式下的伪布尔函数构成的一个伪布尔函数的集合,记为#f(x1, x2, …, xn)。
定义1.3 对于从{0, 1}n到S的伪布尔函数f(x1, x2, …, xn),ADD是一个有向无环图,它用来表示伪布尔函数族#f(x1, x2, …, xn),满足:
(1)S为ADD代数结构的有限值域,且S⊆Z(整数集合)。
(2) 节点分为根节点、终节点和内部节点3类。终节点集合为T。对于∀t∈T,s(t) 均被标识为值域S中的一个元素。
(3) 每个非终节点都满足四元组属性 (fu, var, left, right),fu表示非终结点u所对应的伪布尔函数,var表示非终结点u标记变量;标识节点u的var=0时,对应0-分支子节点和连接弧0-边;high标识节点u的var=1时,多对应1-分支子节点和连接弧1-边。
(4) 每个节点都对应唯一的函数fu。
(5) 在给定变量序x1, x2, …, xn下,任何一条有向路径上,每个变量都必须依照变量序所限定的次序至少出现一次。
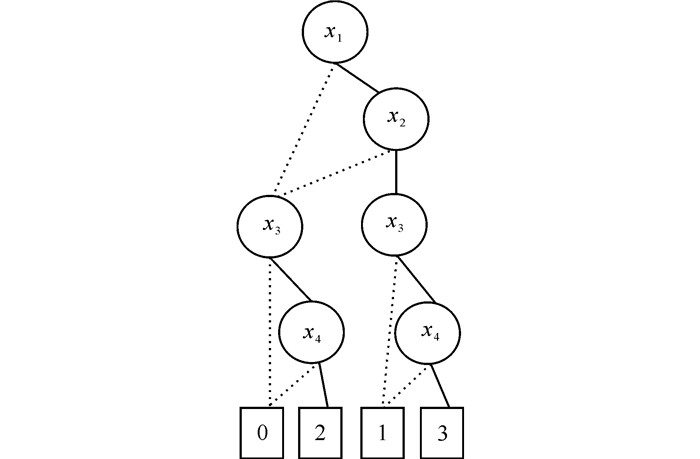
例如,伪布尔函数f(x1, x2, x3, x4)=x1x2+2x3x4,在变量序π:x1 < x2 < x3 < x4的ADD如图 1所示。
|
图 1 伪布尔函数f(x1, x2, x3, x4)=x1x2+2x3x4的ADD表示 Fig.1 ADD for pseudo-Boolean functions f(x1, x2, x3, x4)=x1x2+2x3x4 |
图是由顶点集和顶点间的二元关系集合 (边的集合或弧的集合) 组成的数据结构,通常可以用G= < V, E>来表示,V和E分别表示图的顶点集与边集。
两个图的公共子图通常用来定义两个图之间的距离,而最大公共子图是通过删除节点个数或者边数得到,最大公共子图分为基于边的最大部分子图和基于点的最大公共导出子图 (MCIS)。本研究主要研究基于点的最大公共导出子图,在图中寻找两个图之间所包含的最大节点数的公共子图,即为最大公共导出子图 (MCIS)。
定义2.1 已知两个图结构G和G′,如果存在另外一个图结构g,满足g⊆G,g⊆G′,并且不存在图结构g′(g′⊆G,g′⊆G′),使得|g′|≥|g|,则称g是图G和G′的最大公共子图,记为MCIS (G, G′)。
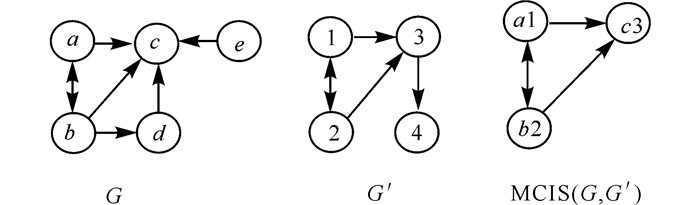
如图 2所示定义两个图G和G′,它们的最大公共子图[15]为g=MCIS (G, G′)。
|
图 2 图G、G′和MCIS (G, G′) Fig.2 The diagrams of G, G′ and MCIS (G, G′) |
在最大公共子图求解过程中,为提高求解效率,引入了全局约束all Different,目的是对不同顶点的所有可能的赋值进行约束。由于每条边的二进制约束只包含一对不同的顶点,不存在两个不同的顶点有相同的赋值,所以在全局约束的限制条件下,能更加有效地缩减搜索空间。
定义2.2 对变量x1, x2, …, xn,有
all Different (x1, …, xn)={(d1, …, dn)|∀di∈D(xi), ∀i≠j, di≠dj}。
从语法看,定义一个全局约束all Diff < V, E, V′, E′, L>,则有
(1) 两个变量集:V,V′。
(2) 两个边集:E⊆V×V和E′⊆V′×V′。
(3)L是一组值对 (xu, u),即任意一个顶点在值域中,变量x′所对应的取值,同时,L中任意两个不同的值对 (xu, u) 和 (xv, v),满足xu≠xv,u≠v。
那么从语义上分析,该约束是全局一致性的,比如:对于任意一个值对 (xu, u)∈L,如果存在u′∈D(xu),那么u′=f(u)。
2.3 MCIS的Soft CSP符号模型 2.3.1 MCIS的Soft CSP模型给定两个图,分别为数据图G=(V, E) 和模式图G′=(V′, E′),其中V和V′分别表示两个图中节点的集合,E、E′分别表示两个图中边的集合。最大公共子图要求图G中的变量在G′中都有相应的赋值,同时,相匹配的节点都保持节点之间的邻接关系 (边关系)。所以给定图G中任意两个节点u和v,所对应的变量分别xu和xv,它们的值域分别为D(xu) 和D(xv)。此外定义一个值φ,表示两图中不匹配的节点的值,则对于MCIS进行Soft CSP建模如下:
定义一个四元组Soft CSP〈X, D, C, λ〉,则有
(1) 任意顶点u所对应的变量xu满足:u∈V,即X={xu|u∈V}∪{xφ};
(2) 变量xu的值域满足:
D(xφ)={φ}, ∀u∈V, D(xu)={u′∈V′}∪{φ}。
(3) 给定任意两个变量xu和xv,利用分层约束将约束划分为
硬约束:∀{u, v}⊆V,
Cedge(xu, xv)≡(xu=φ)∨(xv=φ)∨((u, v)∈E⇔(xu, xv)∈E′)。
软约束:全局约束all Diff〈V, E, V′, E′, L〉。
根据Soft CSP的定义,对不满足约束条件的变量和赋值,定义一个代价值为cost (t),表示不匹配的节点所产生的代价,最终目标是在满足约束的条件下使求得的代价值最小 (节点数最多),得到Soft CSP的最优解。
2.3.2 Soft CSP的符号ADD描述给定一个二元Soft CSP P=〈X, D, C, λ〉,为后续表述方便,变量集X中有n个变量,分别用变量下标1, 2, …, n来表示变量,即|X|=n在变量的值域集D中有d=max{|D(xi)|1≤i≤n}。
在Soft CSP的符号ADD表示中,可以用二进制向量X=(x0, …, xl-1) 表示变量集X中的n个变量;用二进制向量V=(v0, …, vm-1) 来表示每个变量域Di中的任意值,其中:l=⌈logn⌉, m=⌈logd⌉,xi, vj∈{0, 1}, i=0, 1, …, l-1, j=0, 1, …, m-1。用二进制向量 (X, V)=(x0, …, xl-1, v0, …, vm-1) 来表示Soft CSP中的任意一元约束ci,其中 (X, V)=(x0, …, xl-1) 和V=(v0, …, vm-1) 分别是变量xi和变量xi在值域D(xi) 中赋值的二进制向量表示。用二进制向量 (X, Y, V, W)=(x0, …, xl-1, y0, …, yl-1, v0, …, vk-1, w0, …, wk-1) 表示Soft CSP中的任意二元约束cij,其中Y=(y0, …, yl-1),W=(w0, …, wk-1) 分是变量xj和变量xj在值域D(xj) 中赋值的二进制向量表示。因此一元和二元约束可以表示为如下的特征函数:
| $ \begin{array}{l} C\left( {X, Y, V, W} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} \lambda \left( {{x_0}\; \wedge \; \cdots \; \wedge \;{x_{t-1}}\; \wedge \;{y_0}, \cdots \; \wedge \;{y_{t-1}}{v_0}} \right.\; \wedge \; \cdots \; \wedge \;{v_{t-1}}\\ \;\;\;\;\;\;\;\;\left. { \wedge \;{w_0}, \cdots \; \wedge \;{w_{m - 1}}} \right), {C_{ij}} \in C, {d_i} \in {D_i}, {d_j} \in {D_j}, \\ \;\;\;\;\;\;\;{d_i}, {d_j} \in D\\ \lambda \left( {{x_0}\; \wedge \; \cdots \; \wedge \;{x_{t - 1}}\; \wedge {v_0}, \cdots \wedge \;{v_{m - 1}}} \right), {C_{ij}} \in C, \\ \;\;\;\;\;\;\;{d_i} \in {D_i}, {d_j} \in {D_j}, \\ \bot, \;\;{C_{ij}} \in C, {d_i} \notin {D_i}或\;{d_j} \notin {D_j}\;或\;{d_i}, {d_j} \notin D, \\ T, {C_{ij}}\; \in C, {d_i} \notin {D_i}或\;{d_j} \notin {D_j}, \\ 0, \;否则, \end{array} \right. \end{array} $ |
其中λ是一元和二元约束的代价值。在特征函数中,若变量i的值不在域Di或者D中,则设λ=Τ,特征函数可由ADD来表示。
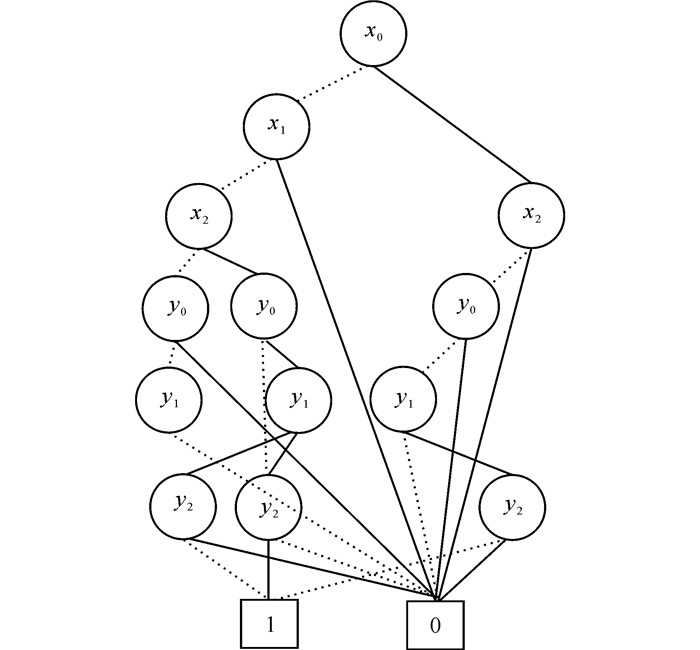
给定数据图G和模式图G′,分别用伪布尔函数表示如下图 3。图 2中的图G,使用如下节点编码:
|
图 3 G图中约束集的ADD表示 Fig.3 ADD formulation of constraint sets in figure G |
| $ a:000, b:001, c:010, d:100, e:110, $ |
其对应的伪布尔函数为
| $ \begin{array}{l} G\left( {x, y} \right) = {{x'}_0}{{x'}_1}{{x'}_2}{{y'}_0}{{y'}_1}{y_2} + \\ {{x'}_0}{{x'}_1}{x_2}{{y'}_0}{{y'}_1}{{y'}_2} + {{x'}_0}{{x'}_1}{{x'}_2}{{y'}_0}{y_1}{{y'}_2} + \\ {{x'}_0}{{x'}_1}{x_2}{{y'}_0}{y_1}{{y'}_2} + {{x'}_0}{{x'}_1}{x_2}{y_0}{{y'}_1}{{y'}_2} + \\ {{x'}_0}{x_1}{{x'}_2}{y_0}{{y'}_1}{{y'}_2} + {x_0}{{x'}_1}{{x'}_2}{{y'}_0}{y_1}{{y'}_2}。\end{array} $ |
在变量序π:x0 < x1 < x2 < y0 < y1 < y2的前提下,根据伪布尔函数的表示,可以将G图中约束集的ADD表示为图 3。
同样对图 3的模式图G′使用如下节点编码
| $ \begin{array}{*{20}{c}} {1:00}&{2:01}&{3:01}&{4:11} \end{array} $ |
其对应的伪布尔函数为
| $ \begin{array}{l} G'\left( {v, w} \right) = {{v'}_0}{{v'}_1}{{w'}_0}{w_1} + {{v'}_0}{{v'}_1}{w_0}{{w'}_1} + \\ {{v'}_0}{v_1}{w_0}{{w'}_1} + {v_0}{{v'}_1}{w_0}{w_1} + {{v'}_0}{v_1}{{w'}_0}{{w'}_1}。\end{array} $ |
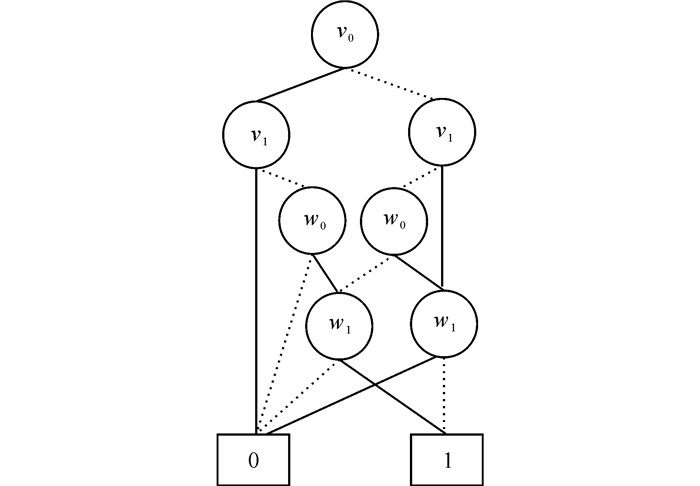
在变量序π:v0 < v1 < w0 < w1的前提下,根据上述的伪布尔函数,可以将G′图中约束集的ADD表示为图 4。
|
图 4 图G′中约束集的ADD表示 Fig.4 ADD formulation of constraint sets in figure G′ |
运用深度优先分支定界法 (DFBB) 结合ADD符号算法对Soft CSP进行求解。DFBB算法的基本思想是按照变量实例化顺序,依次对问题中变量进行实例化,在搜索过程中保存最优完全实例化t,此时最优代价用cost (t) 表示。同时,在每次实例化一个变量时,比较当前赋值的总代价和最优代价,如果当前赋值代价小于最优代价cost (t),则继续下一个变量,否则选择该变量值域中的其他值来进行实例化。算法会有回溯的过程,即对于当前变量值域为空时,表示由部分实例化t扩展不能得到最优解,执行回溯,对上一层进行实例化,并更新下界值,直至找到最优解。
根据MCIS的Soft CSP模型,最大公共导出子图求得的是节点数最多的公共子图, 所以,根据模型定义一个节点不匹配数λ(φ)。在DFBB搜索过程中,对每个变量进行依次赋值时,如果出现不满足约束 (不匹配的节点),则记为λ(φ)=cos (t)=1,否则记为λ(φ)=cos (t)=0。同时,求解过程中,利用深度优先搜索对变量进行赋值时,只要出现不匹配的节点,用φ表示,即表示该变量的取值为φ。然后继续对下一个变量进行实例化,直至对所有空间搜索完毕,算法执行结束,得到一组或者多组解,找到匹配节点数对最多的解,即λ(φ) 值最小的解。
基于DFBB的符号ADD算法的流程如图 5所示。

|
图 5 基于DFBB的符号ADD算法流程 Fig.5 A flow diagram of symbolic ADD algorithm based on DFBB |
基于DFBB的基本思路,结合ADD符号算法,对MCIS的Soft CSP模型进行求解,同时为了验该算法的正确性和可行性,运用实例进行分析,求解的主要步骤如下:
(1) 对问题进行建模,给定MCIS的Soft CSP模型Soft CSP〈X, D, C, λ〉。设定变量选取顺序,构建变量序π,并将约束集表示为符号ADD形式。
(2) 采用基于DFBB算法的ADD符号技术进行求解,对于上述两图的变量集、值域集和约束集分别表示为
①变量集:
| $ \begin{array}{l} \;\;\;\;\;\;X = \left\{ {{{x'}_0}{{x'}_1}{{x'}_2}, {{x'}_0}{{x'}_1}{x_2}, {{x'}_0}{x_1}{{x'}_2}, {x_0}{{x'}_1}{{x'}_2}, } \right.\\ \left. {{x_0}{x_1}{{x'}_2}} \right\} \cup \left\{ \varphi \right\}。\end{array} $ |
②值域集:
| $ D = \left\{ {{{v'}_0}{{v'}_1}, {{v'}_0}{v_1}, {v_0}{{v'}_1}, {v_0}{v_1}} \right\} \cup \left\{ \varphi \right\}。$ |
③约束集表示为G(x, y) 和G′(v, w)。
在ADD算法中,Soft CSP的初始目标值上界用ub表示,且有ub=T,下界用lb表示,且lb=⊥。按照变量实例化顺序,对数据图中的顶点变量{a, b, c, d, e}依次进行实例化。
首先赋值t={},则lb=0,ub=5,从X中选择一个待实例化变量x0′x1′x2′(变量xa),并从X中删去变量x0′x1′x2′,并进行赋值。当xa=v0′v1′时,此时更新待实例化变量集和当前值域,则有
变量集:X1={x0′x1′x2, x0′x1x2′, x0x1′x2′, x0x1x2′}∪{xφ};值域:D1={v0′v1, v0v1′, v0v1}∪{φ};
继续对xb进行实例化,xb=v0′v1,则此时
变量集:X2={x0′x1x2′, x0x1′x2′, x0x1x2′}∪{φ};值域集D2={v0v1′, v0v1}∪{φ};
此时判断以上取值是否满足约束条件,C(xa, xb)={v0′v1′v2′v0′v1′v2}。根据符号ADD操作规则,判断 (xa, xb) 是否满足边约束,由如下所示的符号ADD操作来实现:
a→b边约束为C(xa, xb)=x0′x1′x2′y0′y1′y2。
b→a边约束为C(xb, xa)=x0′x1′x2y0′y1′y2′。
1→2边约束为C(1, 2)=v0′v1′w0′w1。
判断是否满足约束条件,将边a→b约束与图G中的约束集G(x, y)ADD进行ADD符号操作中的∧操作 (合取操作),用F表示得到的约束图。判断得到的结果,如果结果为相应的边约束的ADD表示,那么,该变量的赋值满足Soft CSP中的强约束Cedge,例如:
边a→b:F(a→b)=x0′x1′x2′y0′y1′y2∧G(x, y)ADD=x0′x1′x2′y0′y1′y2;
边b→a:F(b→a)=x0′x1′x2y0′y1′y2′∧G(x, y)ADD=x0′x1′x2′y0′y1′y2,
边1→2:F(1→2)=v0′v1′v2′v0′v1′v2∧G′ADD=v0′v1′v2′v0′v1′v2。
通过操作得知,〈xa, 1〉和〈xb, 2〉满足约束条件,更新目标值的上界和下界,lb=0小于ub,继续对变量xc、xd进行赋值,xc=v0v1′,则有变量集:X3={x0x1′x2′, x0x1x2′}∪{φ}。值域集D2={v0v1}∪{φ}。
同样对边a→b、b→c、1→3、2→3进行约束条件判断,结果表明〈xc, 3〉满足约束条件。
当xd=v0v1时,变量集:X4={x0x1x2′}∪{φ}。值域集D2={}∪{φ}。
同样对边a→c、b→c、1→3、2→3进行约束条件判断,结果表明〈xd, 4〉不满足约束条件,则xd=φ。同理对xe进行赋值,可以得到xe=φ,此时已经对变量全部实例化,得到d, e即为不匹配的节点,更新目标值的上界和下界,分别为lb=ub=2。求解得到的一组解为{xa=1, xb=2, xc=2, xd=φ, xe=φ},此时约束代价值为λ(φ)=2。根据DFBB算法,可以得知当前值域为空,算法进行回溯,继续对变量重新进行赋值。在这个过程中,Soft CSP的目标值不断更新,最终求得的每组解,都会产生一个代价值。通过比较,取λ(φ) 值最小的解为问题的最优解,即求得两图之间的最大公共子图。该算例中最小代价值为λ(φ)=2,即最大匹配节点数为3,所以问题的最优解为{xa=1, xb=2, xc=3},从而求得最大公导出子图。
3 结论从理论上分析,一方面约束满足模型能够充分的对问题的结构信息、约束关系进行分析和刻画。另一方面ADD符号技术极大地改善了伪布尔函数和有限域取值的函数的描述能力,具有高效紧凑和容易操作的优点,减少问题的空间需求,能够减缓状态爆炸问题。
基于此,本研究对图结构进行的ADD刻画,实现了以较小的空间存储一定规模的有向图结构。求解过程中,在Soft CSP建模中引入边和全局约束等约束条件,对变量和相应的取值进行约束,同时采用ADD符号技术和深度优先分支定界法的思想,使得在算法能有效缩减搜索空间,从而提高问题的求解效率,最终求得最大公导出子图。
| [1] |
于静, 刘燕兵, 张宇, 等. 大规模图数据匹配技术综述[J]. 计算机研究与发展, 2015, 52(2): 391-409. YU J, LIU Y B, ZHANG Y, et al. Survey on large-scale graph pattern matching[J]. Journal of Computer Research and Development, 2015, 52(2): 391-409. |
| [2] |
LEVI G. A note on the derivation of maximal common subgraphs of two directed or undirected graphs[J]. Calcolo, 1973, 9(4): 341-352. DOI:10.1007/BF02575586 |
| [3] |
MCGREGOR J J. Backtrack search algorithms and the maximal common subgraph problem[J]. Software Practice and Experience, 1982, 12(1): 23-34. DOI:10.1002/(ISSN)1097-024X |
| [4] |
KRISSINEL E B, HENRICK K. Common subgraph isomorphism detection by backtracking search[J]. Software Practice and Experience, 2004, 34(6): 591-607. DOI:10.1002/(ISSN)1097-024X |
| [5] |
SUTERS W H, ABU-KHZAM F N, ZHANG Y, et al.A new approach and faster exact methods for the maximum common subgraph problem[M]//WANG L S.Computing and combinatorics.Berlin Heidelberg:Springer, 2005.
|
| [6] |
ABU-KHZAM F N, SAMATOVA N F, RIZK M A, et al.The maximum common subgraph problem:Faster solutions via vertex cover[C]//Proceedings of 2007 IEEE/ACS international conference on computer systems and applications.Amman:IEEE, 2007, 367-373.
|
| [7] |
NIRMALA P, LEKSHMI R S, NADARAJAN R. Vertex cover-based binary tree algorithm to detect all maximum common induced subgraphs in large communication networks[J]. Knowledge and Information Systems, 2016, 48(1): 229-252. DOI:10.1007/s10115-015-0874-z |
| [8] |
NDIAYE S N, SOLNON C.CP models for maximum common subgraph problems[M]//LEE J.Principles and practice of constraint programming-CP 2011.Berlin Heidelberg:Springer, 2011:637-644.
|
| [9] |
MINOT M, NDIAYE S N.Searching for a maximum common induced subgraph by decomposing the compatibility graph[C]//Bridging the gap between theory and practice in constraint solvers, CP2014-workshop.Lyon, France, 2016.
|
| [10] |
徐周波, 古天龙, 常亮, 等. 加权约束满足问题的符号ADD求解算法[J]. 模式识别与人工智能, 2011, 24(1): 14-21. XU Z B, GU T L, CHANG L, et al. Symbolic ADD algorithms for weighted constraint satisfaction problem[J]. Pattern Recognition and Artificial Intelligence, 2011, 24(1): 14-21. |
| [11] |
徐周波. 约束满足问题的符号算法及其在装配规划中的应用研究[D]. 西安: 西安电子科技大学, 2011. XU Z B.Research on symbolic algorithm for constraint satisfaction problem and their application in assembly planning[D].Xi'an:Xidian University, 2011. |
| [12] |
古天龙, 徐周波. 有序二叉决策图及应用[M]. 北京: 科学出版社, 2009. GU T L, XU Z B. Ordered binary decision diagram and its application[M]. Beijing: Science Press, 2009. |
| [13] |
BRYANT R E. Symbolic boolean manipulation with ordered binary-decision diagrams[J]. ACM Computing Surveys, 1992, 24(3): 293-318. DOI:10.1145/136035.136043 |
| [14] |
BAHAR R I, FROHM E A, GAONA C M, et al. Algebric decision diagrams and their applications[J]. Formal Methods in System Design, 1997, 10(2/3): 171-206. DOI:10.1023/A:1008699807402 |
| [15] |
ZAMPELLI S.A constraint programming approach to subgraph isomorphism[D].Louvain:Université Catholique de Louvain, 2008.
|
 2017, Vol. 33
2017, Vol. 33 

