【研究意义】K最近邻 (K-Nearest Neighbor, KNN) 算法是数据挖掘“十大经典算法”之一[1]。KNN算法是在一组历史数据记录中, 寻找一个或者若干个与当前记录最相似的历史记录的已知特征值, 来预测当前记录的未知或者遗失特征值[2]。KNN是基于统计的分类方法[3],如果待分类样本在特征空间中的k个最相似 (即特征空间中最邻近) 的样本中的大多数样本属于某一个类别,则该样本也属于这个类别。因此具有简单直观、无需先验统计知识、性能优越的特点,得到了广泛应用。但是传统的KNN算法是一种懒惰的学习方法,具有以下缺点:1) 在样本较大以及特征属性较多时,分类的效率就大大降低;2) 参数k值只能由经验设置,并且对某一个数据集分类效果较好的取值对于其他数据集可能并没有很好的分类效果。【前人研究进展】为了克服传统KNN算法的缺点,学者们提出了许多针对KNN的改进算法。这些算法大致可以分为两类。一类是通过优化或者降维来减少样本之间相关性的计算,以提高分类的效率。如胡元等[4]提出了一种基于区域划分的KNN文本快速分类算法,该算法是将训练样本集按空间分布划分成若干个区域,然后根据测试样本与各个区域之间的位置关系快速查找其k个近邻,大大降低了KNN算法的计算量。林啟锋等[5]提出结合同义向量聚合和特征多类别的改进KNN分类算法,该算法明显提高了文本分类效率和分类的精度。耿丽娟等[6]提出多层差分KNN算法,该算法对已知样本数据类域进行分层,大大降低了无效的计算量,提高了分类的准确性。另一类是通过改进参数k取值的方法,提高分类准确率。Sun和Huang[7]提出对测试样本用其最近邻样本的k值。首先对训练集中的每一个样本训练一个能将它正确分类的最小的k值,然后对测试样本计算最近邻,选用其最近邻的k值来作KNN分类。孙可等[8]提出引入稀疏学习理论,利用训练样本重构测试样本的方法。重构过程中使用样本间的相关性,利用投影变换矩阵w确定KNN算法中的k值。该算法的缺点是k值是全局的,即对所有的测试样本都用同一个k值,这对于分布不均匀的样本集是不合理的,会影响分类的准确率。杨柳等[9]提出一种自适应的大间隔近邻分类算法,该算法将自适应选择k值引入到大间隔近邻分类算法中,减少了k值的选择对分类性能的影响。黄少滨等[10]提出一种自适应最近邻的聚类融合算法,该算法能够根据数据分布的密度,为每一个数据点自动的选择合适的最近邻数。【本研究切入点】在上述研究的基础上,针对现有的KNN算法选取k近邻时采用固定k值的缺点,对每一个测试样本选取不同的k近邻,将自适应选取k值的方法引入到KNN算法中,提出了一种基于局部密度和纯度的自适应k近邻算法。本研究直接考虑样本间的相关性,在KNN算法中直接由数据本身驱动选取k值,避免了人为设定k值对分类准确率的影响。【拟解决的关键问题】对于不同的测试样本k的取值也不固定,通过计算测试样本局部密度和纯度来间接地控制k的取值,使得每个测试样本都由它的k(不固定) 个相关的最近邻样本预测,分类的准确性得到提高。
1 KNN算法KNN算法[11]是Cover和Hart于1968年提出的,该算法的思路:1) 计算出待分类样本与已知类别的训练样本之间的距离或者相似度;2) 找到距离或者相似度与待分类样本数据最近的k个邻居;3) 根据这k个邻居所属的类别来判断待分类样本数据的类别。如果待分类样本数据的k个邻居中大多数属于某一个类别,那么待分类的测试样本也属于这个类别。
定义1(相似度) 向量空间模型下,我们把样本表示成向量,测试样本X={X1, X2, X3…Xm},Y={Y1, Y2, Y3…Yn},Xi=(Xi1, Xi2, Xi3…Xid),Yi=(Yi1, Yi2, Yi3…Yid),其中,d是样本属性的个数,m是测试样本X的个数,n是训练样本Y的个数。
我们采用欧氏距离来确定样本的相似性。欧氏距离的计算公式为
| $ {\rm{distance}}\left( {{X_i},{Y_i}} \right) = \sqrt {\sum\limits_{j = 1}^d {{{\left( {{X_{ij}} - {Y_{ij}}} \right)}^2}} } 。$ | (1) |
由定义1可知,样本Xi与Yi的欧氏距离度量了两个样本的相似程度。当Xi与Yi距离越小,两个样本的相似程度越高。
KNN算法流程:
步骤1:准备数据,设定k值;
步骤2:构造一个大小为k的按距离从大到小的优先级队列priorityQueue,存储最近邻的训练元组。从训练元组中选取前k个元组作为最近邻元组的初始值,用公式 (1) 分别计算测试元组到这k个元组的距离,然后将训练元组的序号和距离存入priorityQueue;
步骤3:遍历整个训练元组集,计算测试元组与当前训练元组的距离L,将L与优先级队列中的最大距离Lmax进行比较。如果L≥Lmax,那么舍弃该训练元组,遍历下一个训练元组。如果L < Lmax,则删除优先级队列中最大距离的元组,将当前训练元组存入priorityQueue中;
步骤4:遍历结束,计算priorityQueue中k个元组的多数类,并将其作为测试元组的类别;
步骤5:测试元组集测试完毕后计算分类准确率,继续设定k值重新训练,最后取分类准确率最高的k值。
针对传统的k近邻算法中k需要人工指定的缺点,孙可等[8]提出引入稀疏学习理论,利用训练样本重构待分类样本的方法,寻找投影变换矩阵W,然后利用得到的W确定待分类样本分类所需的k值,进而进行k近邻分类,完成了k值是根据样本特性自动选定的功能。但该算法也有不足之处:k值是固定的,也就是说对于每一个待分类样本使用的k值都一样。但是在实际应用中,这种采取固定k值的方法经常是不合理的。
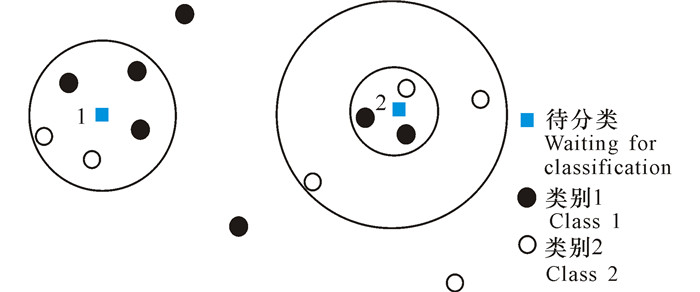
如图 1所示,当k=5时,根据k近邻算法可以得到2个样本空间 (图 1中两个实线圆圈)。其中待分类样本1的k个最近邻样本选取比较合理,但对于待分类样本2而言,实际上令k=3更为合理 (如虚线圆圈所示),因为虚线圆圈中样本的密度明显比实线圆圈中样本的密度大,如果把它们也作为最近邻样本,很可能会影响到分类准确率。因此本研究认为对于不同的测试样本,k值的选取应该根据样本的密度来决定。为了更准确地学习k值,还应当考虑类别的纯度和k的取值之间的关系。
2 改进的KNN算法 2.1 相关概念定义2 设k代表近邻样本数,ki代表近邻样本中最大类别的样本个数,d为待测样本与第k个近邻样本的距离。称F(k) 为待测样本的k的可信度,计算公式如下:
| $ F\left( k \right) = k/d + {k_i}/k。$ | (2) |
如果F(k) 越大,k的可信度越高。公式 (2) 由两部分组成:第一,距离待测样本单位长度上样本的个数 (也就是样本的密度),如果密度越大,k的可信度越高;第二,待测样本的k近邻样本中最大类别所占的比重 (也就是纯度),如果纯度越大,k的可信度越高。k的可信度越高,待测样本的近邻样本数的取值越好。
为了使KNN算法中k值不再固定,本研究从k值的选取进行改进。算法的思路:对待测样本的每一个近邻样本计算k的可信度,利用可信度来控制k的取值。
2.2 算法的步骤基于局部密度和纯度的自适应k近邻算法的步骤如下:
输入:测试样本X={X1, X2, X3…Xm},训练样本Y={Y1, Y2, Y3…Yn}。
输出:测试样本X的类别属性。
步骤1:用公式 (1) 计算出测试样本Xi与每一个训练样本Yi的距离distance;
步骤2:对每一个测试样本Xi按照距离distance大小排序,然后依次保存在数组juli[]中;
步骤3:对于任意的测试样本Xi(i∈[1, m])//设h的初始值为-1
for j=1 :10
{ if juli[j]==0 & & juli [j+1]==0
j++
else if juli[j]==0 & & juli [j+1]!=0
break
else //设max为F (j) 的最大值,h是max对应的k值
{ if max > F (j)
{ max=F (j)
h=j }
else
j++}
}
if (h==-1) k[i]=j;
else k[i]=h;
得到每一个待测试样本Xi对应的的k值k[i];
步骤4:对于任意的测试样本Xi计算出k个元组的多数类,并将其作为测试元组的类别。
2.3 算法的实现下面用一个例子说明算法的实现过程。
例1 表 1是Glass数据集的一部分,随机抽出15条数据 (X1-X15) 为训练集,后两条 (X16和X17) 为测试数据,前9个属性为条件属性,最后一个属性为类别。
| 表 1 训练集与测试样本 Table 1 Training set and testing samples |
下面用本文的算法来判断X16和X17的类别。
步骤1:计算测试样本X16与训练样本间的距离。由公式 (1) 得到X16与训练样本X1-X15的欧式距离分别为{2.049,2.114,2.3,1.013,1.902,5.394,1.034,2.4,1.8,2.3,0.615,2.771,1.978,0.866,0.595}。
步骤2:按距离大小排序:{0.595,0.615,0.866,1.013,1.034,1.8,1.902,1.978,2.049,2.114,2.3,2.3,2.4,2.771,5.394}
步骤3:按公式 (2) 计算测试样本X16对应的k的可信度,选取出可信度最大的k值来选取近邻样本。则
F(1)=1/0.595+1/1=2.68,
F(2)=2/0.615+2/2=4.25,
F(3)=3/0.866+3/3=4.46,
F(4)=4/1.013+3/4=4.69,
F(5)=5/1.034+3/5=5.44,
F(6)=6/1.8+3/6=3.83,
F(7)=7/1.902+3/7=4.109,
F(8)=8/1.978+4/8=4.54,
F(9)=9/2.049+4/9=4.84,
F(10)=10/2.114+4/10=5.13。
比较求得的各个k的可信度,可判断出当k=5时,可信度最大。所以测试样本X16对应的k值为5。
步骤4:根据上一步求得的k值,可判断测试样本X16的类别为3,得到正确的类别判断。
同理,计算出X17对应的k值为1,判断出测试样本X17类别为1,得到正确的类别判断。
对于测试样本X16和X17,根据传统的KNN算法,所有测试样本的近邻数是一样的,如果k的取值都是5,那么对于X16没什么影响,可以得到正确的分类结果。但是对于X17,可以得到5个近邻:X5,X14,X4,X8,X9,其中2个为类别1,2个为类别2,1个为类别3,可能会得到错误的分类结果。
通过上述例子的演算结果可以看出,对于不同的测试样本选择合适的k值,能够更好地判断出测试样本的类别。通过综合考虑测试样本的局部密度以及最大类所占的比重,可以使测试样本选择可信度高的k值,使得测试样本的k值是通过学习样本的相关性得到的,而不是人为设定的,对于不同的测试样本选取的k值也不固定,从而提高了分类的准确率。
3 实例验证 3.1 数据来源本研究选用的7个数据集全部来自UCI数据库 (http://archive.ics.uci.edu/ml/datasets.html),考虑到选取数据集的一般性,我们选取了二类数据集和多类数据集。实验采用eclipse软件,在PC机上进行编程操作。数据集信息统计如表 2所示。
| 表 2 数据集信息统计 Table 2 Data set information statistics |
实验采用五折交叉验证法 (Cross validation) 进行分类准确度评价。数据集被随机均分成5个子集,本研究提出的算法在每个数据集上运行5次,每次取一个子集作为测试集,其余的4个子集作为训练集,然后取5次实验结果的平均值作为该数据集的分类结果。
本实验采用的评价指标是分类的正确率,正确率越高表明分类的效果越好。分类正确率的计算公式如下:accuracy=ncorrect/n,其中ncorrect为测试样本中正确分类的个数,n为测试样本的总数。
将每组数据使用本文提出的算法和传统的KNN算法、AdaNN算法[7]进行比较,此处把传统的KNN算法称为算法1,把AdaNN算法称为算法2,把基于局部密度和纯度的自适应k近邻算法称为算法3。在相同的条件下比较3种算法的分类准确率,为使所得结果更加准确,我们采用的是五折交叉法。令算法1中的k=5,而算法2和算法3的k值是由数据驱动产生,无需事先处理。
3.3 结果与分析如表 3所示,表中加粗的数据表示每一个数据集对应的最好的分类准确率。对表 3进行分析,可以发现:
| 表 3 分类准确率比较 Table 3 Accuracy comparison |
1) 对于表 3中的同一组数据,算法3得到的分类准确率相比于算法1和算法2要高,说明本文提出的自适应k值的选取方法是可行的,能够得到较高的分类准确率。
2) 对于不同的数据集,无论样本个数的大小,属性个数的多少,算法3都能得到较理想的结果,说明本文提出的基于局部密度和纯度的自适应k近邻算法是可行的。
4 结论本研究提出了一种基于局部密度和纯度的自适应k近邻算法,有效地解决了传统KNN分类算法的两个缺陷:k值需要事先给定且固定;未考虑样本之间的相关性。该算法的思想是根据测试样本的局部密度和最大类别的纯度来计算k的可信度,选取k的最大的可信度来选择测试样本的近邻,实现了k值的选取由数据本身驱动,无需人为设定。因此,本算法可以用于无法通过经验或者需要长时间实验选取k值的情况,大幅度减少选取k值的时间。最后通过对UCI标准数据集实验验证表明,与已有的两种算法对比,本文的方法可以得到较高的分类准确率。虽然取得了一些有益的结果,但是在对不平衡数据集如何更好的选取k值和搜索近邻问题上仍然需要进一步深入研究和探讨。
| [1] |
WU X D, KUMAR V, QUINLAN J R, et al. Top 10 algorithms in data mining[J]. Knowledge and Information Systems, 2008, 14(1): 1-37. DOI:10.1007/s10115-007-0114-2 |
| [2] |
俞蓓, 王军, 叶施仁. 基于近邻方法的高维数据可视化聚类发现[J]. 计算机研究与发展, 2000, 37(6): 714-720. YU B, WANG J, YE S R. Visual clustering for high dimensional data based on nearest neighbor[J]. Journal of Computer Research and Development, 2000, 37(6): 714-720. |
| [3] |
MITCHELL H B, SCHAEFER P A. A "soft" K-nearest neighbor voting scheme[J]. International Journal of Intelligent Systems, 2001, 16(4): 459-468. |
| [4] |
胡元, 石冰. 基于区域划分的kNN文本快速分类算法研究[J]. 计算机科学, 2012, 39(10): 182-186. HU Y, SHI B. Fast kNN text classification algorithm based on area division[J]. Computer Science, 2012, 39(10): 182-186. |
| [5] |
林啟锋, 蒙祖强, 陈秋莲. 结合同义向量聚合和特征多类别的KNN分类算法[J]. 计算机科学, 2013, 40(12): 55-58. LIN Q F, MENG Z Q, CHEN Q L. KNN text categorization algorithm based on semantic-vector-combination and multiclass of feature[J]. Computer Science, 2013, 40(12): 55-58. |
| [6] |
耿丽娟, 李星毅. 用于大数据分类的KNN算法研究[J]. 计算机应用研究, 2014, 31(5): 1342-1344. GENG L J, LI X Y. Improvements of KNN algorithm for big data classification[J]. Application Research of Computers, 2014, 31(5): 1342-1344. |
| [7] |
SUN S L, HUANG R Q.An adaptive k-nearest neighbor algorithm[C]//Proceedings of 2010 seventh international conference on fuzzy systems and knowledge discovery.Piscataway, Shandong:IEEE, 2010:91-94.
|
| [8] |
孙可, 龚永红, 邓振云. 一种高效的K值自适应的SA-KNN算法[J]. 计算机工程与科学, 2015, 37(10): 1965-1970. SUN K, GONG Y H, DENG Z Y. An efficient SA-KNN algorithm with adaptive K value[J]. Computer Engineering & Science, 2015, 37(10): 1965-1970. |
| [9] |
杨柳, 于剑, 景丽萍. 一种自适应的大间隔近邻分类算法[J]. 计算机研究与发展, 2013, 50(11): 2269-2277. YANG L, YU J, JING L P. An adaptive large margin nearest neighbor classification algorithm[J]. Journal of Computer Research and Development, 2013, 50(11): 2269-2277. |
| [10] |
黄少滨, 李建, 刘刚. 一种基于自适应最近邻的聚类融合方法[J]. 计算机工程与应用, 2012, 48(19): 157-162. HUANG S B, LI J, LIU G. Clustering ensemble algorithm based on adaptive nearest neighbors[J]. Computer Engineering and Applications, 2012, 48(19): 157-162. |
| [11] |
LIU Y, CHEN G S.KNN algorithm improving based on cloud model[C]//Proceedings of 2010 2nd international conference on advanced computer control (ICACC).Changsha:IEEE, 2010:63-66.
|
| [12] |
邓振云, 龚永红, 孙可, 等. 基于局部相关性的kNN分类算法[J]. 广西师范大学学报:自然科学版, 2016, 34(1): 52-58. DENG Z Y, GONG Y H, SUN K, et al. A kNN classification algorithm based on local correlation[J]. Journal of Guangxi Normal University:Natural Science Edition, 2016, 34(1): 52-58. |
 2017, Vol. 33
2017, Vol. 33