【研究意义】以节点表示实体,边表示实体之间的关系,就可以将现实世界中的很多系统抽象为复杂网络,如人际关系网、论文合作网、电影明星合作网、博客引用网、电话通讯网等[1]。这些复杂网络往往具有潜在的社区结构,比如同一社区内的节点连接紧密,而社区之间的节点连接则较稀疏。对复杂网络中的社区结构进行发现与分析,可以很好地理解其结构和行为,具有重要的研究价值与意义[2-3]。【前人研究进展】已有许多学者从不同角度对如何发现网络中的社团结构问题进行了研究,比较经典的社区挖掘算法有GN算法[4]、谱分析思想的算法[5]、层次距离算法[6]、边集聚系数法[7]等,Fortunato[8]也对复杂网络社区挖掘算法进行了详细的介绍和研究。传统的社团发现算法大多存在算法复杂度较高的问题,难以有效处理包含大量节点的社交网络。有的算法需要预先确定网络中的社区数目以及社区的大致规模,限制了算法的实际应用效率。Raghavan等[9]提出了一种基于标签传播的社区发现算法,即标签传播算法 (Label propagation algorithm,LPA),该算法能够在接近线性时间内查找出网络中的社区结构,在处理大规模的网络时具有很好的时间效率,且不需要事先知道网络中有多少个社区、社区规模如何,因此受到越来越多的关注。
LPA算法是一种基于标签传播机制的启发式算法,其主要思想在于初始化时为网络中每个节点赋予一个独特的标签,根据每个节点的邻居节点集合的标签分布对该节点的标签进行迭代更新,通过多次迭代,网络中各节点的标签会趋于稳定,那些具有相同标签的节点则组合成同一社区。在现实的社交网络图中,节点与节点之间的关系不仅仅是存在边或者不存在边这两种状态,还有联系紧密程度的区分。LPA算法在更新节点标签时,标签选择的策略仅考虑了邻接点中相同标签的个数,忽略了邻接点联系的紧密程度,有很大的局限性,Zhang等[10]提出了相干邻居亲近度 (Coherent neighborhood propinquity) 的概念来度量网络中任意节点对间的亲近程度。Lou等[11]将相干邻居亲近度引入标签传播算法,提出了CNP-LPA算法,该算法并不直接在原始网络上传播标签,而是对网络进行预处理,计算网络中任意节点对的CNP值,基于得到的CNP网络传播标签。在更新标签时,使用节点对的CNP值对标签进行加权,选择权值最大的标签进行更新。然而,CNP-LPA算法进行预处理时只考虑到了网络节点间的亲密程度,没有考虑到节点间依赖度。【本研究切入点】在实际的社交网络中,影响力较小的节点所属的社区往往依赖于本区域内影响力较大的节点 (核心节点)。此外,通过预处理得到的CNP网络,边的数目相比原始网络往往会大大增加,这就使得后续标签传播过程花费的时间明显增加。【拟解决的关键问题】针对上述问题,本研究在CNP-LPA算法基础上,引入节点间依赖度,提出一种改进算法CNP-LPA+,其核心思想是在预处理阶段合并所有依赖度高的节点 (冗余节点),仅仅保留网络中的核心节点,根据得到的核心CNP网络传播标签,传播过程完成后,将有相同标签的核心节点归入同一社区,冗余节点所属社区与本区域内核心节点所属社区保持一致。选取空手道关系网络、美国政治书籍网络、科学家引用网络等6组社交网络作为测试数据集,使用模块度Q作为评估LPA、CNP-LPA、CNP-LPA+ 3种算法发现质量的评价函数。模块度Q是最广泛使用的衡量社区发现质量的函数,由Newman和Girvan[12]提出。实验结果证明CNP-LPA+算法在6组数据集上均取得了最高的Q值,显著提高了社区发现的质量,并减少了标签传播过程花费的时间。
1 朴素标签传播算法 (LPA) 及其改进 1.1 朴素LPA以节点表示实体,边表示实体之间的关系,就可以将社交网络抽象成一个无向简单图,形式化描述为G=(V, E),其中V(v∈V) 表示节点集,E(e∈E) 表示边集,且满足E⊂V×V。
G中任意的节点v(v∈V),LPA算法初始时都为其分配一个唯一的标签cv,用于表示节点v所属的社区,N(v) 表示节点v的邻居集合,更新规则如式 (1) 所示:
| $ {c_v} = \arg \mathop {\max }\limits_l \left| {{N^l}\left( v \right)} \right|, $ | (1) |
|Nl(v)|表示v邻居节点集合中标签为l的节点个数,每个节点的标签被更新为其数量最多的邻居节点所拥有的标签。LPA算法的时间复杂度为O(t|E|),其中t用来表示迭代次数,|E|表示网络中的边数,算法时间复杂度接近线性,在处理大规模的社交网络时具有很好的效率。LPA算法标签的更新策略忽略了网络中节点与节点之间联系的紧密程度,Lou等[11]将相干邻居亲近度引入LPA算法,提出了CNP-LPA算法。
1.2 CNP-LPA 1.2.1 相干邻居亲近度Zhang等[10]提出了相干邻居亲近度 (Coherent Neighborhood Propinquity) 的概念,用来度量网络中任意节点对 (v1, v2) 之间的亲近程度,如式 (2) 所示:
| $ \begin{array}{l} P\left( {{v_1},{v_2}} \right) = \left| {E\left( {{v_1},{v_2}} \right)} \right| + \left| {N\left( {{v_1}} \right) \cap } \right.\\ \left. {N\left( {{v_2}} \right)} \right| + \left| {E\left( {G\left[ {N\left( {{v_1}} \right) \cap N\left( {{v_2}} \right)} \right]} \right)} \right|, \end{array} $ | (2) |
P(v1, v2) 表示网络中任意节点对 (v1, v2) 的CNP值,它由3个部分组成。|E(v1, v2)|表示节点v1与v2直接相连的边的数目。|N(v1)∩N(v2)|表示v1与v2共享的邻居节点数,它的值等于v1邻居节点集合与v2邻居节点集合的交集大小。|E(G[N(v1)∩N(v2)])|表示包含在v1与v2共享邻居节点集合的交集节点间连接的边的数目。P(v1, v2) 值越大,说明节点v1, v2之间联系越紧密,也越可能同属于一个社区。
图 1a中vA与vB共享的邻居节点有3个,如图 1b所示,|N(vA)∩N(vB)|=3。vA与vB共享邻居节点C、D、E之间连接的边有2条,如图 1c所示,|E(G[N(vA)∩N(vB)])|=2。图 1a中,vA与vB间存在边,|E (vA, vB)|=1。因此,对于图 1a中节点对 (vA, vB),P(vA, vB)=1+3+2=6。
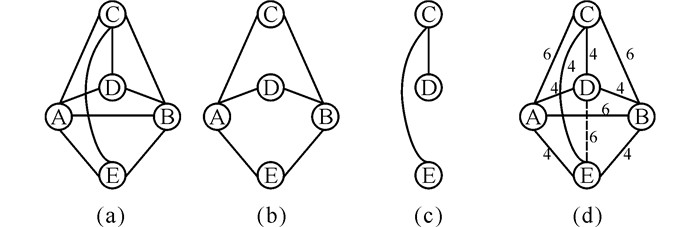
|
图 1 相干邻居亲近度 Fig.1 Coherent Neighborhood Propinquity |
同理对于节点对 (vD, vE),|N(vD)∩N(vE)|=3,|E(G[N(vD)∩N(vE)])|=3。而在图 1a中,vD与vE并不存在边,|E(vD, vE)|=0,P(vD, vE)=0+3+3=6。求出网络中所有节点对的CNP值后,就可以将原始网络转换为相应的CNP网络。图 1d是图 1a生成的CNP网络,边上的数字表示相关节点对的CNP值。图 1中原始网络G中边的数目|E|=9,而相应的CNP网络Gp中边的数目|Ep|=10。
1.2.2 CNP-LPA算法CNP网络形式化描述为Gp=(V, Ep, P),V(v∈V) 表示节点集,Ep(ep∈Ep) 表示边集。v1, v2∈V, 且ep(v1, v2)∈Ep,则P(v1, v2) 表示节点对 (v1, v2) 的CNP值。
CNP-LPA算法在预处理阶段将原始网络G转换为CNP网络Gp,并基于Gp传播标签。更新标签时,根据节点对的CNP值对标签进行加权。两个节点之间的CNP值越大,表示它们联系越紧密,它们的标签对对方的影响也就越大,选择总的CNP值最大的标签进行更新,更新规则如式 (3) 所示:
| $ {c_v} = \arg \mathop {\max }\limits_l \sum\limits_{s \in {v^l}} {P\left( {v,s} \right)} 。$ | (3) |
在实际的社交网络中,影响力较小的节点所属的社区往往依赖于本区域内影响力较大的节点。可以发现图 2中v12所属的社区一定和v1所属社区保持一致,同样v16所属社区依赖于v33和v34,本研究只考虑单个节点之间的依赖度,将节点间依赖度引入CNP-LPA算法,提出了CNP-LPA+算法。
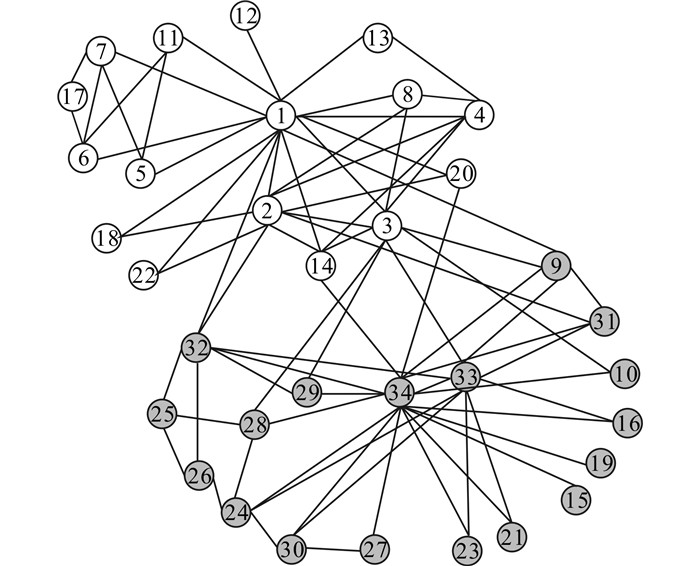
|
图 2 空手道关系网络图 Fig.2 Zachary's karate club network |
节点间依赖度定义:无向简单网络G=(V, E), ∀u, v∈V,且e(u, v)∈E,则D(u, v) 表示节点u依赖于节点v的程度,D(u, v) 值越大,节点u越依赖于节点v,节点u所属的社区越可能与节点v所属社区保持一致。
给出一种直观的方法来度量节点间依赖度,节点u的覆盖范围包含在节点v覆盖范围之中的程度就是节点u依赖于节点v的程度。
| $ D\left( {u,v} \right) = \frac{{\left| {N\left( u \right) \cap N\left( v \right)} \right| + 1}}{{\left| {N\left( u \right)} \right|}}。$ | (4) |
排除没有邻居节点的孤立节点,则D(u, v)∈(0, 1],当D(u, v)=1时,表示节点u在网络中的覆盖范围完全包含在节点v的覆盖范围之中。
冗余节点定义:u∈V, ∃v∈N(u),使D(u, v)≥c(c为给定的阈值),说明节点u覆盖范围大部分包含在节点v的覆盖范围中,确定节点v的社区就可以确定节点u所属的社区,称节点u为冗余节点。
核心节点定义:u∈V, ∀v∈N(u), 使D(u, v) < c,即节点u的任意邻居节点v的覆盖范围都不能大部分包含节点u的覆盖范围,称节点u为核心节点。
2.2 核心CNP网络核心CNP网络形式化描述为Gc=(Vc, Ec, Pc),Vc(vc∈Vc) 表示核心节点集,Ec(ec∈Ec) 表示核心边集,且满足Ec⊂Vc×Vc。∀v1, v2∈Vc, 且ec(v1, v2)∈Ec,则Pc(v1, v2) 表示核心节点对 (v1, v2) 的CNP总值。
图 3a是空手道关系网络的一部分,图 3b是其对应的CNP网络,可以看出后者相比前者增加了5条边。为了避免这个问题,作如下约定:原始网络G=(V, E) 中的节点对 (v1, v2),如果v1, v2间存在边,则保留该节点对的CNP值;如果不存在边,则将该节点对的CNP值清零。图 3a中节点对 (v1, v17),(v5, v6), (v5, v17), (v7, v11), (v11, v17) 间均不存在边,因此忽略这5对节点的CNP值,图 3c就是图 3a对应简化的CNP网络。在图 3a中,D(v17, v6)=D(v17, v7)=1,v17的覆盖范围被完全包含在v6或者v7的覆盖范围中,v17所属的社区可以与v6保持一致,也可以并入v7所属的社区。D(v5, v1)=D(v11, v1)=1,v5与v11的覆盖范围完全包含在v1的覆盖范围中,则v5与v11可以直接并入v1所属的社区。在后续标签传播过程中不再考虑v5, v11, v17。
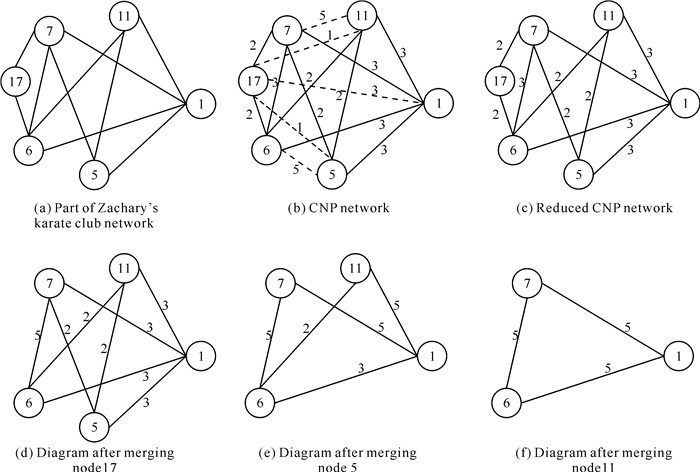
|
图 3 冗余节点合并过程 Fig.3 Process of merging redundant nodes |
CNP-LPA+算法的主要思想就是在预处理阶段时,首先将原始网络转换为简化的CNP网络,在简化CNP网络的基础上,合并冗余节点到相应的核心节点,冗余节点与第三方节点之间的CNP值继承到相应的核心节点上。接着根据预处理阶段得到的核心CNP网络传播标签,传播过程完成后,将有相同标签的核心节点归入同一社区,冗余节点所属社区与相应的核心节点保持一致。合并过程如下:
在图 3c的基础上,将节点17并入节点6,并更新节点间的CNP值:
a) 令P(v6, v17)=0;
b) P(v6, v7)=P(v6, v7)+P(v7, v17)=3+2=5;
c) P(v7, v17)=0;
更新后如图 3d所示,接着在图 3d基础上将节点5并入节点1,并更新节点间的CNP值:
d) 令P(v1, v5)=0;
e) P(v1, v7)=P(v1, v7)+P(v5, v7)=3+2=5;
f) P(v5, v7)=0;
g) P(v1, v11)=P(v1, v11)+P(v5, v11)=3+2=5;
h) P(v5, v11)=0;
更新后如图 3e所示,接着在图 3e基础上将节11并入节点1,并更新节点间的CNP值:
i)P(v1, v11)=0;
j)P(v1, v6)=P(v1, v6)+P(v6, v11)=3+2=5;
k)P(v6, v11)=0。
到此为止,合并全部完成。图 3f就是图 3a对应的核心CNP网络,其边数仅仅只有3条。预处理阶段结束后,CNP-LPA+算法在得到的CNP核心网络基础上传播标签,更新标签的规则如式 (5),其中v∈vc,vcl表示v的邻居节点中标签为l的核心节点集合,Pc(v, s) 即核心节点对 (v, s) 之间的CNP总值。
| $ {c_v} = \arg \mathop {\max }\limits_l \sum\limits_{s \in v_c^l} {Pc\left( {v,s} \right)} 。$ | (5) |
这里给出CNP-LPA+算法的伪代码:
Input:网络G(V, E),节点间依赖度阈值c。
步骤1:计算每条边e(u, v) 对应节点对 (u, v) 间CNP值,得到G的简单CNP网络;
步骤2:根据给定的阈值c,合并所有冗余节点,得到核心CNP网络Gc=(Vc, Ec, Pc);
步骤3:给每个核心节点v∈Vc赋予唯一的标签;
步骤4:迭代次数t=1;
步骤5:随机排序核心节点集Vc;
步骤6:基于Gc=(Vc, Ec, Pc) 传播标签,根据式 (5) 更新标签,采用异步更新的方式来避免出现标签震荡;
步骤7:若t达到设置的最大迭代次数或每个核心节点标签CNP权值达到最大,算法结束;否则t=t+1,返回步骤5。
算法运行完成后,将具有相同标签的核心节点归入同一社区,冗余节点所属社区与相应的核心节点保持一致。CNP-LPA+算法同时考虑到了节点间亲近度与节点间依赖度,在预处理阶段就将冗余节点并入本区域内的核心节点,并基于核心CNP网络传播标签,不仅减少了标签传播花费的时间,更重要的是在社区发现准确性方面有了显著的提高。
2.4 CNP-LPA+算法时间复杂度分析步骤1中∀e(u, v)∈E,需要计算节点对 (u, v) 的CNP值P(u, v),时间复杂度为O(|E|);
步骤2中需要合并所有冗余节点,∀v∈V,v是否为冗余节点,只需要在其邻居节点范围内寻找是否存在节点包含了v的大部分覆盖范围。如果是则合并冗余节点v,时间复杂度为O(|E|);
步骤3中初始化核心节点标签时间为O(|V|);
步骤5中随机排序核心节点序列O(|V|);
步骤6中一次标签传播时间为O(|E|);
步骤7中生成社区的时间为O(|V|)。
可见CNP-LPA+算法与标准LPA算法同样具有接近线性的时间复杂度。
3 实例验证本研究选取6组真实的社交网络数据集分别对LPA算法、CNP-LPA算法、CNP-LPA+算法进行测试分析。表 1是这些数据集的介绍。由于这些算法的结果都具有一定的随机性,因此所有的实验都进行10次,结果取平均值。3种算法均使用C++语言实现,实验环境为Windows10,Inter(R) Core(TM) i5-4690 CPU@3.50GHz,8 GB内存。
| 表 1 真实社交网络数据集 Table 1 Real-world networks with community structure |
CNP-LPA算法在预处理阶段将原始网络G转换为CNP网络Gp,而CNP-LPA+算法则需转换为核心CNP网络Gc(注意给定不同的阈值参数c,G所得到的核心CNP网络Gc也不同,实验中阈值c默认取0.8),G、Gp、Gc边数的不同,后续标签传播过程花费时间也不同。图 4中蓝色柱条代表CNP网络,红色柱条代表核心CNP网络,柱条上的值等于两者边数比上原始网络边数的比值。karate数据集原始网络有78条边,其对应的CNP网络则有343条边 (343/78=4.4),而当阈值c取0.8时,它的核心CNP网络仅有32条边 (32/78=0.41)。
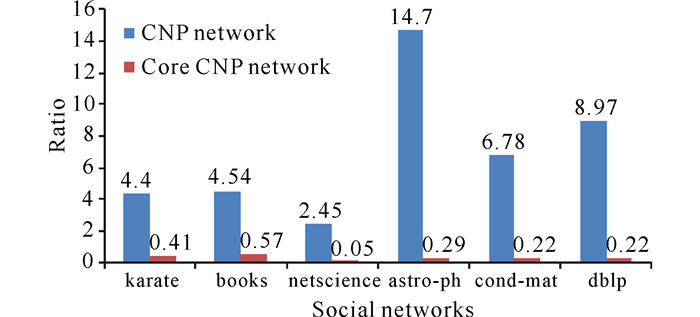
|
图 4 CNP网络与核心CNP网络边数 Fig.4 Edges of CNP network and core CNP network |
从图 4可以看出6组数据集的CNP网络Gp边数均远远超过了原始网络G的边数,其中astro-ph数据集Gp边数是G边数的14.7倍,是6组数据集中最高的。与此同时所有数据集的核心CNP网络Gc的边数都小于G的边数,其中netscience数据集Gc的边数仅是G边数的1/20,只保留了原始网络中最关键的边。
预处理阶段结束后,CNP-LPA算法基于CNP网络传播标签,而CNP-LPA+算法基于核心CNP网络传播标签,显然边数越少标签传播越快。设置最大迭代次数为20次,6组数据集在CNP-LPA算法与CNP-LPA+算法下传播标签平均所花费时间如表 2所示。
| 表 2 标签传播时间 Table 2 Time of spreading label |
由表 2可以看出,当网络数据集中节点与边数较少时,CNP-LPA算法传播时间与CNP-LPA+传播时间的差距尚处于可以容忍的范围内,但当节点数增大时,传播时间的差距就变得非常明显。如astro-ph数据集,CNP-LPA算法标签传播平均需要29 s,而CNP-LPA+算法平均仅需要0.257 s;特别是dblp数据集,在20次的迭代范围内,CNP-LPA算法标签传播并没有结束,而此时所花费时间已经超过129 s,而CNP-LPA+算法则正常运行结束,平均花费时间只有2.056 s,明显优于前者。
使用模块度Q作为评价社区质量的指标,分别对LPA、CNP-LPA、CNP-LPA+ 3种算法进行测试分析,结果如表 3所示。
| 表 3 模块度Q对比 Table 3 Average modularity of LPA, CNP-LPA, CNP-LPA+ |
由表 3可以看出,除了前2个数据集,CNP-LPA算法全部优于LPA算法,而CNP-LPA+算法在所有数据集上优于LPA和CNP-LPA算法。特别是在karate, books, astro-ph数据集上,在CNP-LPA算法相比LPA算法并无提升的情况下,CNP-LPA+算法获得了很好的效果,达到或者明显超过了LPA算法划分的准确性。而在netscience, cond-mat, dblp 3组数据集上,在CNP-LPA算法相比LPA算法已经获得了明显的提升的基础上,CNP-LPA+算法相比CNP-LPA算法获得了进一步的提升,这充分说明了CNP-LPA+算法的有效性。
综上所述,CNP-LPA+算法相比较CNP-LPA算法不仅减少了标签传播的时间,最重要的是在社区发现准确性方面有了显著的提高。
4 结论本研究在分析CNP-LPA算法的特点和不足的基础上,提出了一种新的基于相干邻居亲近度的标签传播算法CNP-LPA+,该算法同时考虑到相干邻居亲近度与节点间依赖度,并基于核心CNP网络传播标签,相比CNP-LPA算法不仅减少了标签传播过程所花费的时间,进一步提高了社区发现的准确性。CNP-LPA+算法仍然保持近似线性的时间复杂度。在接下来的工作中,将考虑更多节点间依赖度的度量方法,比较不同方法对标签传播算法的影响,还可以将节点间依赖度应用到具有重叠现象的社区发现等问题中。
| [1] |
林友芳, 王天宇, 唐锐, 等. 一种有效的社会网络社区发现模型和算法[J]. 计算机研究与发展, 2012, 49(2): 337-345. LIN Y F, WANG T Y, TANG R, et al. An effective model and algorithm for community detection in social networks[J]. Journal of Computer Research and Development, 2012, 49(2): 337-345. |
| [2] |
刘大有, 金弟, 何东晓, 等. 复杂网络社区挖掘综述[J]. 计算机研究与发展, 2013, 50(10): 2140-2154. LIU D Y, JIN D, HE D X, et al. Community mining in complex networks[J]. Journal of Computer Research and Development, 2013, 50(10): 2140-2154. |
| [3] |
SERRANO M Á, BOGUÑÁ M, SAGUÉS F. Uncovering the hidden geometry behind metabolic networks[J]. Molecular Biosystems, 2011, 8(3): 843-850. |
| [4] |
GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826. DOI:10.1073/pnas.122653799 |
| [5] |
CAPOCCI A, SERVEDIO V D P, CALDARELLI G, et al. Detecting communities in large networks[J]. Physica A:Statistical Mechanics and Its Applications, 2005, 352(2/3/4): 669-676. |
| [6] |
BOCCALETTI S, LATORA V, MORENO Y, et al. Complex networks:Structure and dynamics[J]. Physics Reports, 2006, 424(4/5): 175-308. |
| [7] |
RADICCHI F, CASTELLANO C, CECCONI F, et al. Defining and identifying communities in networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(9): 2658-2663. DOI:10.1073/pnas.0400054101 |
| [8] |
FORTUNATO S. Community detection in graphs[J]. Physics Reports, 2010, 486(3/4/5): 75-174. |
| [9] |
RAGHAVAN U N, ALBERT R, KUMARA S. Near linear time algorithm to detect community structures in large-scale networks[J]. Physical Review E, Statistical Nonlinear, and Soft Matter Physics, 2007, 76(3): 036106. |
| [10] |
ZHANG Y Z, WANG J Y, WANG Y, et al.Parallel community detection on large networks with propinquity dynamics[C]//Proceedings of the 15th ACM SIGKDD international conference on knowledge discovery and data mining.York, NY, USA:ACM, 2009.
|
| [11] |
LOU H, LI S H, ZHAO Y X.Detecting community structure using label propagation with weighted coherent neighborhood propinquity[M]//BRESNAN J (ed.).The mental representation of grammatical relations.Massachusetts:MIT Press, 1982:3095-3105.
|
| [12] |
NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2004, 69(2): 026113. |
| [13] |
ZACHARY W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research, 1977, 33(4): 473. |
| [14] |
NEWMAN M E. Modularity and community structu-re in networks[J]. P Natl Acad Sci USA, 2006, 103(23): 8577-8582. DOI:10.1073/pnas.0601602103 |
| [15] |
FIEDLER M. Algebraic connectivity of graphs[J]. Czech Math J, 1973, 23(98): 298-305. |
| [16] |
NEWMAN M E J. The structure of scientific collaboration networks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2001, 98(2): 404-409. DOI:10.1073/pnas.98.2.404 |
| [17] |
Laboratory for Web algorithmics[EB/OL].[2016-11-12]. http://law.di.unimi.it/datasets.php.
|
 2017, Vol. 33
2017, Vol. 33 

