【研究意义】高速公路在一定程度上缓解了交通压力,但是由于收费站的设置,使得收费站路段成为高速公路的交通瓶颈。因此,如何提高高速公路收费站路段的通行能力是亟需解决的问题。目前,我国已基本实现全国高速公路收费站ETC联网,建立全国ETC联网运营管理机制。在正常交通情况下,ETC车道禁止停车,但是目前很多收费站的ETC通道的建设并不完善,部分ETC通道仍然采用“人工/ETC”混合收费方式[1],造成高速公路收费站还是偶尔出现拥堵现象。因此,研究收费站全面开通ETC通道的必要性,对提高收费站路段的通行能力有重要意义。【前人研究进展】元胞自动机交通流模型主要考虑单个车辆在相互作用下的个体行为,通过研究每辆车的前后作用,了解交通流动特性[2]。Nagel和Schreckenberg于1992年提出了一种一维元胞自动机交通流模型——NaSch模型,适用于模拟高速公路交通流。朱留华等[3]基于NaSch模型,建立了关于单车道电子收费和人工收费系统的元胞自动机交通流模型并进行数值模拟,同时还对两种收费共存系统的交通流特性进行分析。对交通能耗的研究国内外学者已开展了大量的工作。最早是在跟驰模型中探讨交通能耗,随后,利用CA模型对交通能耗进行研究,田欢欢等[4]、梁玉娟[5-6]、韦兰香等[7]则在元胞自动机NaSch模型的基础上,对交通流的能耗进行研究。【本研究切入点】针对当前高速公路存在的“人工/ETC”混合收费方式,从车辆动能损失的角度对收费站路段的交通特性进行理论研究的文献较少。【拟解决的关键问题】基于元胞自动机NaSch模型,建立存在混合收费方式的收费站路段的车辆能耗模型,根据实际的交通状况,取定人工收费车辆在收费站的滞留时间和车辆的随机延迟概率,研究人工收费车辆的比例系数和收费站前减速路段的长度对车辆能耗的影响,发现比例系数越大,减速路段越长,车辆的能耗值越小,道路交通越拥堵。
1 模型的建立假设车辆行驶在一条长度L=7.5 km的单车道上(图1),道路由1 000个元胞构成,每一个元胞对应的实际道路长度7.5 m。行车道上的车辆自左向右行驶,每一个元胞在每一时刻处于空闲或容纳一辆车的状态,有斜线的元胞为有车状态,空白元胞为无车状态,灰色元胞为收费站前的减速路段,其长度用La表示,黑色元胞为收费站的位置(第600个元胞),用Ls表示。另外,系统采用周期性边界条件,即车辆行驶在一条环形路上。在本文中,长度单位均以元胞为单位做无量纲化处理。
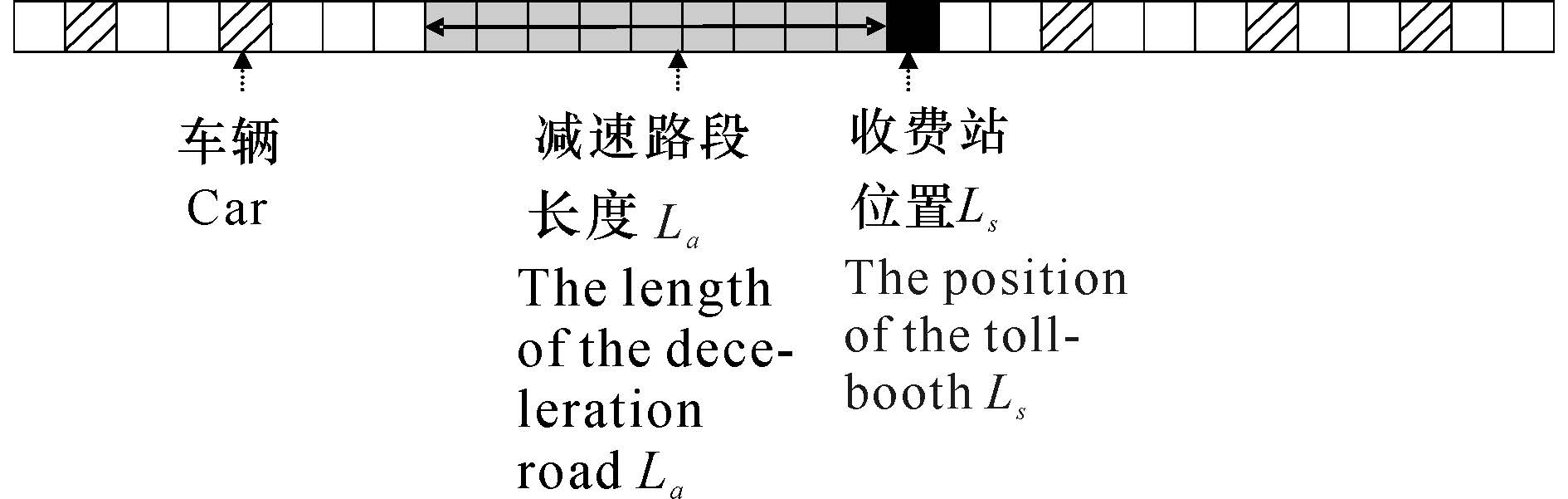
|
图 1 有收费站的高速公路路段模型示意图 Fig.1 Schematic model of the highway with to llbooth |
假设道路有人工收费和ETC收费两种模式,人工收费车辆必须在收费站停车付费,ETC收费车辆经过收费站时不需要停车。所有车辆行驶到收费站前时,首先判断站内是否有车辆正在付费,如果有,则必须停车等待,否则:(1)ETC收费车辆继续行驶;(2)人工收费车辆进站付费,达到规定停靠时间T后离开。
1.2 修正NaSch 模型的演化规则(1)确定性加速过程:vnt→min (vn(t)+1,vmax );
(2)确定性减速过程:vn(t)→min (vn(t),gapn(t));
(3)以概率P随机减速过程:vn(t)→max (vn(t)-1,0);
(4)位置更新过程:xn(t)→xn(t)+vn(t)。其中,vn(t)和xn(t)分别为车道上第n辆车在t时刻的速度和位置,xn+1(t)则是车道上第n+1辆车在t时刻的位置,gapn(t)=xn+1(t)-xn(t)-1是t时刻第n辆车与前方紧邻车辆之间的元胞数;P为车辆的随机延迟概率。每一辆车的状态由该车的速度v来表示,v∈[0,vmax],即速度可在0与最高车速之间取任意值。当车辆行驶在减速路段上时,用vmax1表示其最大速度,令vmax1=1cell/s(27 km/h),车辆在其他区域上行驶时,用vmax2表示其最大速度,令vmax2=5cell/s(135 km/h)。又假设车辆在所有区域的随机延迟概率都相同,令P=0.25。
1.3 车辆能耗若车辆的质量为m,速度为v,则其动能为mv2/2。当车辆作减速运动时,其动能减少,即能量消耗,简称能耗。文中第n辆车从t-1到t时间内的能耗[4]为
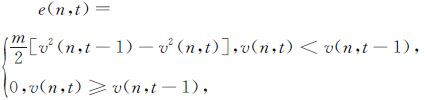
|
则每辆车在单位时间内的平均总能耗为
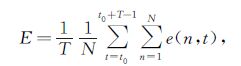
|
其中N是车道上的总车辆数,T是统计时间,t0是驰豫时间。
根据NaSch模型的演化规则,车辆的减速行为分为确定性减速和随机减速。确定性减速是由于车辆的速度大于其与前车的距离,为了避免碰撞必须减速;随机减速是由于驾驶员本身的习惯、道路的状况、气候等原因而减速。我们把由于确定性减速而产生的车辆能耗称为相互作用能耗,把由于随机减速而产生的车辆能耗称为随机减速能耗,两者之和为总能耗。
2 数值模拟及分析基于以上模型,利用C语言编写程序,在模拟中假设长L的行车道上共有N辆车,车辆密度ρ=N/L,平均车流量J=ρV,而车辆的平均速度为
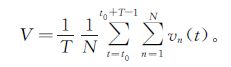
|
在数值模拟计时开始时,让人工收费车辆和ETC收费车辆以一定的比例和一定的车辆密度ρ随机分布在一维1 000个元胞链L上。每一次运行取40 000时间步进行数值模拟,为消除暂态的影响,开始的20000时间步不进行统计,之后的20 000时间步内的每一时间步对速度νn(t)和能耗e(n,t)进行统计,而每一次运行的平均速度和平均能耗即将20 000时间步的速度和能耗对时间求平均。考虑到存在随机问题,为减小随机误差,对20次运行取平均值。
在实际的交通中,人工收费车辆在高速公路进口处的收费站领卡,而在高速公路出口处的收费站交卡、交费后才驶离。领卡耗时较短,对道路交通的影响较小;交卡、交费耗时较长,对道路交通的影响较大。故在进行数值模拟时,以交卡、交费耗时作为人工收费车辆在收费站的滞留时间T。经过实际测量发现,车辆在收费站滞留的时间从10.02s到24.83s不等,滞留时间的平均值为16.48s。因此,在进行数值模拟时,人工收费车辆的滞留时间T取值为17s。为方便研究,车辆的质量m取1。
2.1 人工收费车辆比例系数f对车辆能耗的影响取定收费站前减速路段的长度为La=100,改变人工收费车辆的比例系数f进行数值模拟,结果如图 2~6所示。
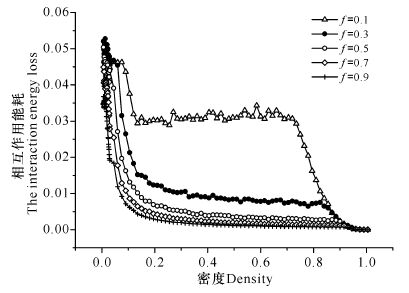
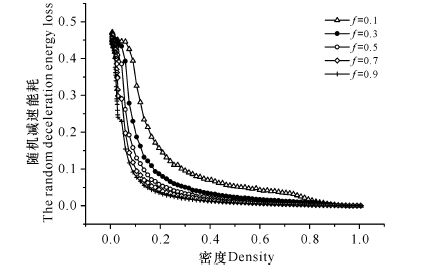
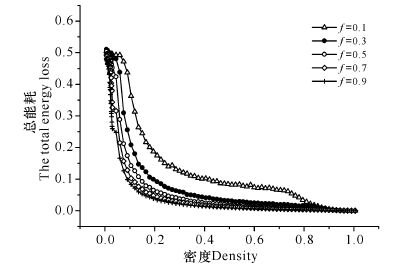
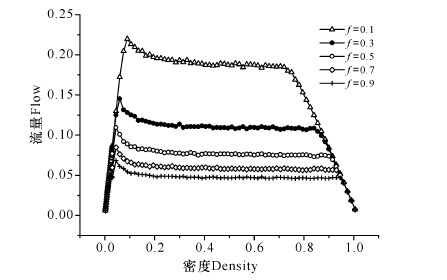
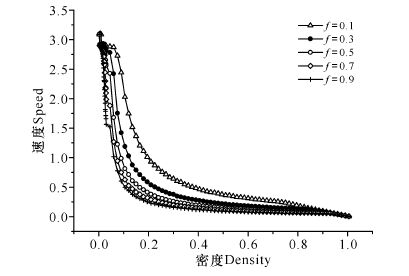
图 2结果显示,在不同的比例系数f下,相互作用能耗均随着密度的增加而逐渐减小到零;在同一密度下,比例系数f越大,相互作用能耗越小。图 3结果显示,在不同的比例系数f下,随机减速能耗均随着密度的增加而逐渐减小到零;在同一密度下,比例系数f越大,随机减速能耗越小。从图 4可以看出,人工收费车辆的比例系数不同,车辆的动能损耗也不同。在同一密度下,f越大,总能耗越小。当取定密度为ρ=0.1,比例系数f分别为0.1,0.3,0.5,0.7,0.9时,对应的总能耗分别为0.44,0.26,0.17,0.13,0.10,此时对应的流量和平均速度也越小(图 5、图 6)。出现此现象,是因为在取定La的情况下,人工收费车辆的比例系数f越大,车辆的平均速度越小,车辆低速跟车行驶的现象越明显,则车辆减速前后的速度差值越小,能耗值越小,说明道路交通越拥堵。
|
图 2 不同比例系数f下的相互作用能耗-密度图(La =100) Fig.2 The interaction energy loss -density plot under different proportional coefficient f(La =100) |
|
图 3 不同比例系数f下的随机减速能耗-密度图(La=100) Fig.3 The random deceleration energy loss-density plot under different proportional coefficient f(La=100) |
|
图 4 不同比例系数f下的总能耗-密度图(La=100) Fig.4 The total energy loss-density plot under differ-ent proportional coefficient f(La=100) |
|
图 5 不同比例系数f下的流量-密度图(La=100) Fig.5 Flow-density plot underdifferent proportional coefficient f(La=100) |
|
图 6 不同比例系数f下的速度-密度图(La=100) Fig.6 Speed-density plot under different proportional coefficient f(La =100) |
从图 4还可以看出,在同一比例系数f下,道路上的车辆密度越大,总能耗值越小。当取定比例系数f=0.5,密度ρ分别为0.1,0.2,0.3,0.5,0.7,1.0时,对应的总能耗分别为0.17,0.06,0.04,0.02,0.01,0.00,此时对应的流量和平均速度也越小(图 5、图 6)。出现此现象是因为,密度小时,车辆数目少,车辆处于自由、高速运动的状态,当车辆发生减速时,减速前后的速度差值大,能耗值也大;当密度增大时,车辆数目增多,车辆之间相互制约的作用越严重,平均速度越小,车辆低速跟车行驶的现象越明显,则车辆减速前后的速度差值越小,能耗值越小,也说明道路交通越拥堵。
2.2 收费站前减速路段的长度La对车辆能耗的影响取定人工收费车辆的比例系数为f=0.5,改变收费站前减速路段的长度La,得到的模拟结果如图 7~11所示。
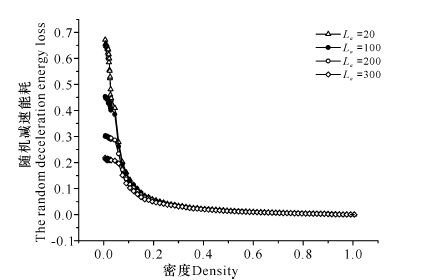
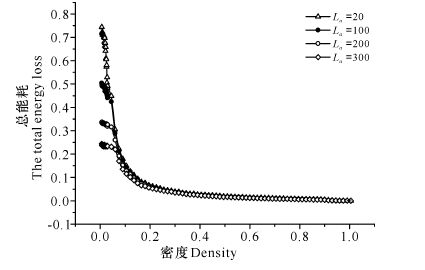
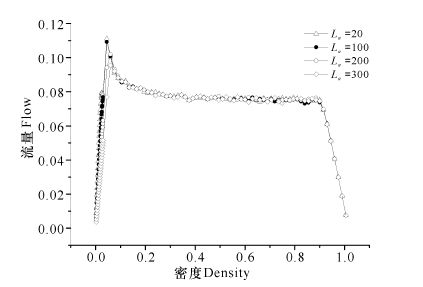
图 7结果显示,在不同的La下,相互作用能耗均随着密度的增加从初值逐渐减小到零;La越大,相互作用能耗的最大值越小。图 8结果显示,在不同的La下,随机减速能耗均随着密度的增加从初值逐渐减小到零;La越大,随机减速能耗的最大值越小。从图 9可以看出,收费站前减速路段的长度La不同,车辆动能损耗的最大值也不同,La分别为20,100,200,300时,对应的总能耗最大值分别为0.74,0.50,0.34,0.24。而在密度约小于0.2时,在同一密度下,La越大,总能耗越小。当取定密度为ρ=0.2,La分别为20,100,200,300时,对应的总能耗分别为0.68,0.48,0.33,0.24,此时对应的流量和平均速度也越小(图 10、图 11)。出现此现象是因为,在取定f的情况下,收费站前减速路段的长度越大,车辆的平均速度越小,车辆低速跟车行驶的现象越明显,则车辆减速前后的速度差值越小,能耗值越小,也说明道路交通越拥堵。而在密度大于0.2时,收费站前减速路段的长度对总能耗几乎没有影响。出现这种现象是因为,当密度增大时,车辆数目增多,车辆之间相互制约的作用严重,平均速度小,车辆处于时停时走的低速跟车行驶状态,道路交通拥堵,此时减速路段的长度La不再影响道路的通行能力。

|
图 7 不同减速路段长度La下的相互作用能耗-密度图(f=0.5) Fig.7 The interaction energy loss-density plot under different deceleration roadlength La(f =0.5) |
|
图 8 不同减速路段长度La下的随机减速能耗-密度图(f=0.5) Fig.8 The random deceleration energy loss-density plot under different deceleration road length La(f=0.5) |
|
图 9 不同减速路段长度La下的总能耗-密度图(f =0.5) Fig.9 The total energy loss-density plot under differ-ent deceleration road length La(f =0.5) |
|
图 10 不同减速路段长度La下的流量-密度图(f=0.5) Fig.10 Flow-density plot under different deceleration road length La(f =0.5) |

|
图 11 不同减速路段长度La下的速度-密度图(f=0.5) Fig.11 Speed-density plot under different deceleration road length La(f=0.5) |
文献[7]研究结果显示,为减少高速公路收费站路段的交通拥堵现象,收费站应该全面采取ETC收费方式,缩短车辆在收费站的滞留时间,提高收费站路段的通行能力,缓解交通压力。事实上,在有人工和ETC收费方式共存的收费站路段上,人工收费车辆的比例系数和收费站前减速路段的长度也会对道路交通产生影响。本文在元胞自动机NaSch交通流模型的基础上,针对人工和ETC收费方式共存的单向单车道的收费站路段提出车辆的能耗公式,在取定人工收费车辆在收费站的滞留时间(T=17s)和车辆随机延迟概率(P=0.25)的情况下,数值模拟周期边界条件下人工收费车辆的比例系数f和收费站前减速路段的长度La对车辆能耗的影响,发现f和La对车辆能耗均有一定程度的影响:
(1) 人工收费车辆的比例系数越大,道路上车辆的能耗值就越小,对应的流量和平均速度也越小,道路交通越拥堵;
(2) 在低密度时,收费站前减速路段越长,道路上车辆的能耗值就越小,对应的流量和平均速度也越小;在中密度和高密度时,收费站前减速路段的长度对车辆能耗没有影响,对流量和平均速度也没有影响。
| [1] |
李国辉,胡丽丽,丁高阳.广东ETC车道“人工/ETC”混合收费方式让快速通行大打折扣[EB/OL].[2015-08-06].http://news.ycwb.com/2015-08/06/content_20507296.htm. LI G H,HU L L,DING G Y.Guangdong ETC Lanes “artificial/ETC” Mixed Charging Methods Let the Rapid Transit Sell at a Discount Greatly[EB/OL].[2015-08-06].http://news.ycwb.com/2015-08/06/content_20507296.htm. |
| [2] |
郭四玲.元胞自动机交通流模型的相变特性研究和交通实测分析[D].南宁:广西大学,2006:15-22. GUO S L.Study on the Characteristics of Phase Transition in Cellular Automaton Models for Traffic Flow and Analysis of Traffic Empirical Data[D].Nanning:Guangxi University,2006:15-22. http://cdmd.cnki.com.cn/article/cdmd-10593-2006174998.htm |
| [3] |
朱留华, 陈时东, 孔令江, 等. 过路收费站对高速公路交通的影响[J]. 物理学报, 2007, 56(10): 5674-5678. ZHU L H, CHEN S D, KONG L J, et al. The influence of tollbooths on highway traffic[J]. Acta Physica Sinica, 2007, 56(10): 5674-5678. |
| [4] |
田欢欢, 薛郁, 康三军, 等. 元胞自动机混合交通流模型的能耗研究[J]. 物理学报, 2009, 58(7): 4506-4513. TIAN H H, XUE Y, KANG S J, et al. Study on the energy consumption using the cellular automaton mixed traffic model[J]. Acta Physica Sinica, 2009, 58(7): 4506-4513. |
| [5] |
梁玉娟. 从动能损失看弯道路段的通行能力[J]. 四川师范大学学报:自然科学版, 2011, 34(3): 355-359. LIANG Y J. Investigation of the traffic capacity in the bend by the loss of kinetic energy[J]. Journal of Sichuan Normal University:Natural Science, 2011, 34(3): 355-359. |
| [6] |
梁玉娟. 基于坡道元胞自动机模型的能耗研究[J]. 广西科学, 2011, 18(1): 44-47. LIANG Y J. Investigation of the energy dissipation based on celluar automatic model of slope[J]. Guangxi Sciences, 2011, 18(1): 44-47. |
| [7] |
韦兰香, 梁玉娟. 收费站对高速公路交通流能耗的影响[J]. 广西科学, 2016, 23(1): 92-96. WEI L X, LIANG Y J. Study on the influence of tollbooth on highway traffic flow’s energy loss[J]. Guangxi Sciences, 2016, 23(1): 92-96. |
 2016, Vol. 32
2016, Vol. 32 


