直流电阻率法是一种广泛应用于浅地表地球物理勘探的方法。该方法通过研究地表或井中建立的稳定电流场分布规律来推断地下电性结构[1-2],多应用于矿产资源勘探[3]、环境监测[4]、水文地质调查[5-6]等领域。传统直流电阻率法主要以探明地下电导率或电阻率分布为目标,而水文地质模型中的岩石电阻率与介质孔隙度、含水饱和度等参数密切相关。理论上,这些参数会影响直流电阻率的正演响应,反之也可以通过响应规律来推断相关参数的地下分布。目前,相关研究中的现有模型在某些情况下能够提供合理的预测,但这些模型普遍依赖于经验参数(如渗透阈值和孔隙度)的选择。这些经验参数的确定往往需要大量实验数据支持,且在不同地质条件下可能具有显著差异,这限制了模型的普适性和预测精度。因此,如何提高模型的普适性和预测精度成为当前研究面临的主要挑战之一[7]。
在水文地质领域,阿尔奇公式(Archie′s formula)常被用于描述岩石电阻率与孔隙度、含水饱和度等参数的关系[8]。该公式不仅在油气勘探中用于精确估算储层的饱和度和孔隙度[8],还被广泛应用于水资源调查和环境监测等领域[9]。近年来,学界围绕阿尔奇公式开展了3个方面研究,一是针对复杂地质条件的公式校正与参数优化[10-12],二是基于该公式的直流电阻率响应机制研究[13-14],三是通过耦合流体介质建模方法提升电性结构表征精度[15],这些进展显著提升了油气储层识别的可靠性[16]。现有电导率模型仍存在两个主要局限,一是模型参数多依赖经验取值,二是对孔隙结构非均质性的表征不足。研究表明,直流电阻率响应主要受流体3个方面的物性调控:①电导率。流体电导率作为影响地层电阻率的主要因素之一,直接决定地层电阻率特征——高电导率流体(如盐水)导致地层电阻率显著降低,而低电导率流体(如油、气)则使地层电阻率升高[16],该特性成为区分含油气层和含水层的关键依据。②黏度。虽不直接影响电阻率,但通过调控流体流动性与空间分布产生间接效应,高黏度流体易形成非均匀分布格局,引发电阻率的空间异质性[17]。③介电常数。通过改变电场传播速度影响测量结果,高介电常数流体(如水)会增加介质的总电容,进而影响电阻率测量结果[18]。实际储层中多相流体(油、水、气)的共存使电阻率响应更趋复杂。研究者们通过多相流体模拟体系,揭示了多相体系对电阻率的协同作用机制[16],并深入讨论了有效介质理论、分形理论和渗流理论等模型在预测微观尺度上多孔介质中两相电导率方面的应用,数值模拟与室内实验的联合验证,为完善电导率预测模型提供了重要支撑[7]。
综上所述,在使用直流电阻率法进行水文勘探时,孔隙度、含水饱和度等流体性质对观测响应存在较大影响。大量实验研究表明,实际电导率数据的分布特征比经验模型的预测结果更为复杂,现有模型算法的适用性和局限性仍需深入探讨。为此,本文首先基于阿尔奇公式建立孔隙度、含水饱和度及溶液电阻率等参数与岩石电阻率的定量关系;其次开展三维直流电阻率正演模拟研究,开发更适用于渗流条件的正演模拟算法;最后通过构建典型砂岩型模型和砂岩型油水模型进行数值模拟,分析不同相态流体条件下孔隙度、含水饱和度及溶液电阻率等参数对正演视电阻率响应的影响规律。研究成果将有助于充分挖掘直流电阻率响应所蕴含的流体分布信息,为渗流场研究提供可靠的技术支撑。
1 直流电阻率有限元正演对于地下均匀分布的稳定电流场,假设在地表放置点电源A,则点电源A在地下均匀半空间产生三维电位u的控制方程为
| $ \nabla \cdot(\sigma \nabla u)=-2 I \delta(A), $ | (1) |
式中,σ为电导率,I为电流大小,δ为狄拉克函数。对于地下半无限空间,存在一个足够大的圆柱面Γ∞,它同地面Γs共同组成封闭区域Ω。此时直流电阻率的边值问题可表述为
| $ \left\{\begin{array}{l} \nabla \cdot(\sigma \nabla u)=-2 I \delta(A) \\ \left.\sigma \frac{\partial u}{\partial \boldsymbol{n}}\right|_{\Gamma_s}=0 \\ \frac{\partial u}{\partial \boldsymbol{n}}+\left.\frac{u \cos \theta}{\boldsymbol{r}}\right|_{\Gamma_{\infty}}=0 \end{array}, \right. $ | (2) |
式中,n为边界外法向方向矢量,θ为点电源A与n的夹角,r为位置矢量。式(2)描述的点源场边值问题等价于下列变分问题[19]:
| $ \left\{\begin{array}{l} F(u)=\int_{\Omega}\left[\frac{1}{2} \sigma(\nabla u)^2-2 I \delta(A) u\right] d \Omega+ \\ \quad \frac{1}{2} \int_{\Gamma_{\infty}} \frac{\sigma \cos (\boldsymbol{r}, \boldsymbol{n})}{\boldsymbol{r}} u^2 d \Gamma \\ \delta F(u)=0 \end{array}\right., $ | (3) |
采用有限单元法对式(3)进行离散求解:
| $ F(u)=\sum F_e(u)=\frac{1}{2} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{K} \boldsymbol{U}-\boldsymbol{U}^{\mathrm{T}} \boldsymbol{P}, $ | (4) |
式中,U为全部节点电位组成的阵列;K为刚度矩阵;P= (0, …, C, …, 0)T,P中只有与电源点A所在节点相对应的元为常数C,其余元均为0。对式(4)求变分并令其等于0,可得线性方程:
| $ K U=P \text { 。} $ | (5) |
为提高三维问题求解的稳定性,本文采用直接解法求解式(5)获得求解域节点电位,进而计算视电阻率。
为检验本文开发的三维直流电阻率正演程序精度,分别以均匀半空间(100 Ω·m)和三层水平层状模型为例,采用二极装置,在点距为3、5、7、10 m条件下,将三维有限元数值解与一维解析解进行对比。均匀半空间的计算结果如表 1所示,解析解与数值解的相对误差绝对值在0.716%-1.811%,平均误差为0.783%,满足5%的容许误差范围要求。
| 点距/m Distance of point/m |
解析解/(Ω·m) Analytical solutions/(Ω·m) |
数值解/(Ω·m) Numerical solutions/(Ω·m) |
相对误差绝对值/% Absolute value of relative error/% |
| 3 | 100.487 | 99.545 | 0.937 |
| 5 | 100.843 | 100.121 | 0.716 |
| 7 | 101.209 | 99.657 | 1.533 |
| 10 | 101.772 | 99.928 | 1.811 |
三层水平层状模型如图 1所示,第一、二层的厚度均为20 m,第三层厚度为∞。各层电阻率依次为100、1 000、100 Ω·m。正演视电阻率计算结果见表 2,解析解与有限元数值解的相对误差绝对值在0.906%-1.925%,平均误差为1.249%,在5%的容许误差范围内。表 1、表 2的计算结果表明,所开发的有限元正演程序具有较高的可靠性。
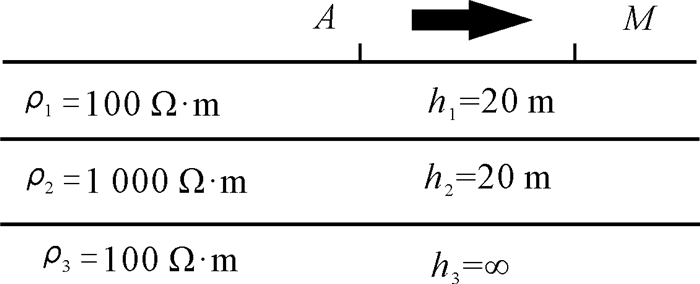
|
| 图 1 三层水平层状模型 Fig. 1 Three-layer horizontal layered model |
| 点距/m Distance of point/m |
解析解/(Ω·m) Analytical solutions/(Ω·m) |
数值解/(Ω·m) Numerical solutions/(Ω·m) |
相对误差绝对值/% Absolute value of relative error/% |
| 3 | 124.524 | 126.921 | 1.925 |
| 5 | 141.282 | 143.055 | 1.255 |
| 7 | 157.954 | 156.523 | 0.906 |
| 10 | 182.485 | 180.345 | 1.173 |
2 基于阿尔奇公式的正演计算
阿尔奇公式是1942年由Archie提出的经典经验公式,用于描述岩石电导率与孔隙度、含水饱和度、岩性之间的关系。其原始形式为地层电阻率因素(地层因子)的表达式:
| $ F=\frac{R_0}{R_w}=\frac{a}{\varphi^m}, $ | (6) |
式中,R0为地层水100%饱和时的地层电阻率,单位为Ω·m;Rw为地层水电阻率,单位为Ω·m;a为与岩性相关的比例系数,φ为岩石孔隙度,m为岩石的胶结指数,均为无量纲[20]。通过变换式(6)可得到地层电阻率表达式[21-22]:
| $ R_t=\frac{a b R_w}{\varphi^m S_w^n}, $ | (7) |
式中,Rt为地层电阻率,单位为Ω·m;b为岩性常数,n为饱和度指数,均为无量纲;Sw为含水饱和度,变化范围为0-1。阿尔奇公式在水文地质领域应用广泛,其通过地层电阻率因数评价孔隙有效性,并利用比例系数和胶结指数来表征不同胶结程度岩石的孔隙贡献[23-24]。岩性、孔隙结构、泥质含量、喉道分选、孔隙类型的变化均会导致岩电参数发生改变。在直流电阻率正演模拟中,可根据式(7)通过孔隙度、含水饱和度等参数计算地层电阻率,进而结合地下电阻率分布推导视电阻率响应ρs。
由式(7)可知,对地层电阻率产生主要影响的参数为孔隙度、含水饱和度以及地层水电阻率。根据调查资料,常见岩石孔隙度为0.1%-28.0%,其中砂岩的孔隙度为1.6%-28.0%,含水饱和度均在0-1变化。地层水电阻率的取值随着充填流体性质的变化而变化,取值在0.1-1 000.0 Ω·m不等。胶结指数反映孔隙度的曲折程度,常取值1.3-2.1。饱和度指数用于校正饱和度微观分布不均匀性,常取值0.3-2.5。充分考虑阿尔奇公式中各参数影响,结合各参数取值范围,得到地层电阻率Rt和岩石孔隙度φ随φ-m的变化趋势曲线[图 2(a)],以及地层电阻率Rt和含水饱和度Sw随Sw-n的变化趋势曲线[图 2(b)]。在参数取值范围内,φ-m、Sw-n与Rt呈正相关,二者影响趋势相似;φ-m、Sw-n分别与φ、Sw呈负相关。综上,地层电阻率的变化特征由参数取值范围及其相互作用决定。岩石孔隙度及孔隙流体性质通过影响含水饱和度和孔隙度,最终改变直流电阻率的视电阻率响应。
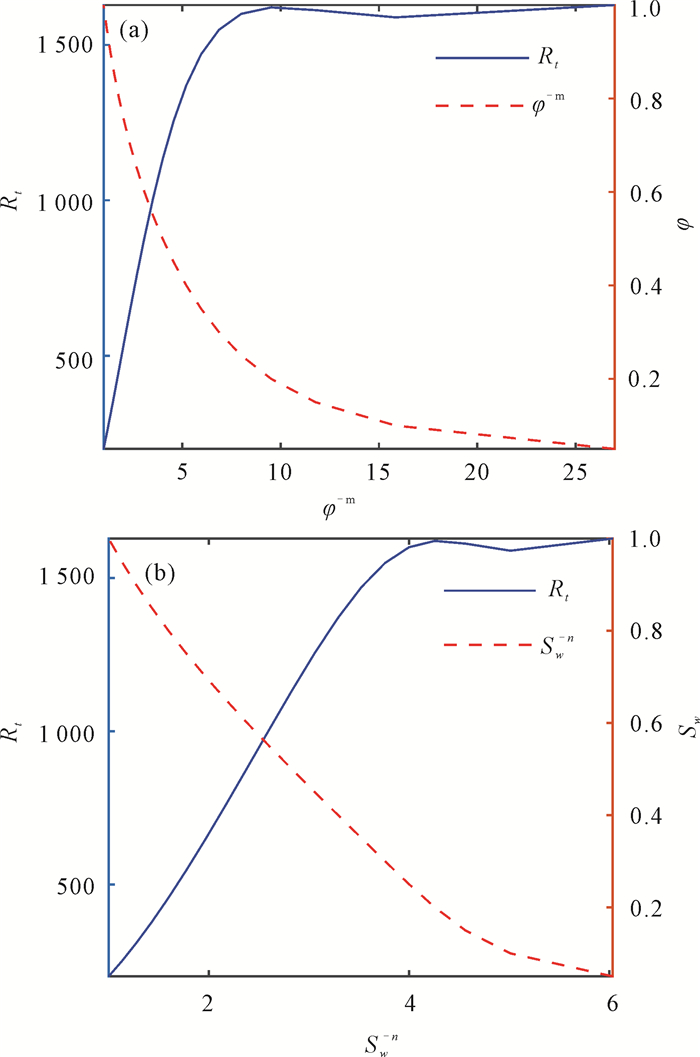
|
| (a) Trends of Rt and φ with respect to φ-m; (b) Trends of Rt and Sw with respect to Sw-n. 图 2 数值变化趋势曲线 Fig. 2 Trend of numerical changes |
3 理论模型计算
模型1:三维砂岩储层模型
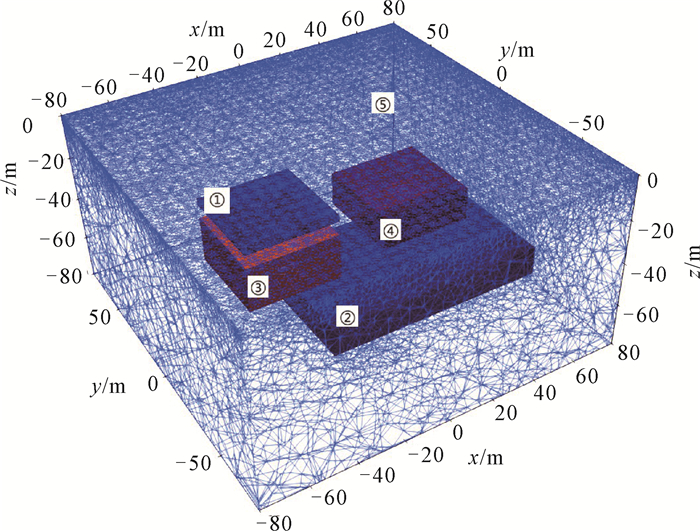
针对常见浅层阶梯状地下水分布特征及砂岩中高阻岩层嵌入情况,设计一个三维砂岩储层模型(图 3)。将均匀背景标记为①;背景空间内上方存在一个块状异常体,标记为②,范围为x=-40 m至20 m,y=-∞至+∞,z=-5 m至-10 m;在其下方为阶梯状异常体③,由两个异常体块组成,范围分别为x=-∞至0 m,y=-∞至+∞,z=-10 m至-15 m和x=-30 m至50 m,y=-∞至+∞,z=-16 m至-21 m。模型参数设置参考内蒙古某地C类储层测井资料[24],详见表 3,其中异常体②表征砂岩中的高阻岩层,异常体③代表高孔隙度、高渗透率储层。图 4为根据参数设置得到的理论地层电阻率Rt的剖面(y=0),可见异常体②表现为高阻特征,异常体③表现为低阻特征。
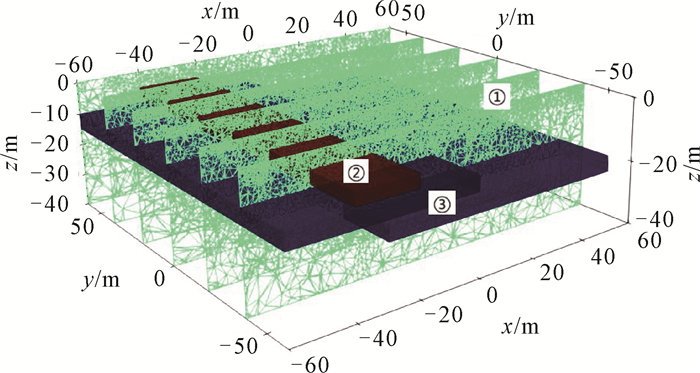
|
| 图 3 三维砂岩储层模型示意图 Fig. 3 3D sandstone reservoir model |
| 序号 No. |
比例系数 a |
岩性常数 b |
胶结指数 m |
饱和度指数 n |
孔隙度 φ |
含水饱和度 Sw |
地层水电阻率/(Ω·m) Rw/(Ω·m) |
地层电阻率/(Ω·m) Rt/(Ω·m) |
| ① | 0.59 | 1.15 | 2.16 | 1.87 | 0.2 | 0.5 | 10.0 | 802.141 8 |
| ② | 0.59 | 1.15 | 2.16 | 1.87 | 0.2 | 0.8 | 50.0 | 1 165.393 2 |
| ③ | 0.59 | 1.15 | 2.16 | 1.87 | 0.2 | 0.8 | 2.0 | 66.615 7 |
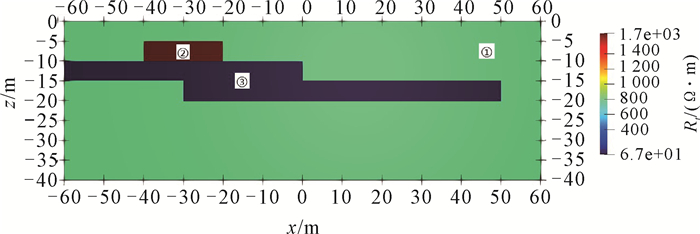
|
| 图 4 三维砂岩储层模型理论地层电阻率Rt剖面(y=0) Fig. 4 Theoretical stratigraphic resistivity Rt profiles of 3D sandstone reservoir model (y=0) |
采用二极装置,在地表以原点0为中心,沿x、y方向布设40×40观测网,极距3 m。正演计算时对地下空间进行非结构四面体网格剖分,单元数为841 106。正演结果见图 5(白色线框标示实际异常体边界)。x为-40 m至-20 m的近地表区域出现明显高视电阻率响应,视电阻率峰值约700 Ω·m,水平位置基本与理论模型中高阻异常体②吻合。x<0 m,z为-5 m至-15 m的区域出现明显低视电阻率响应,左侧响应值440-500 Ω·m;中部(x为-40 m至-20 m)受上方高阻影响,响应值约500 Ω·m;右侧受阶梯状双层异常影响,低视电阻率响应范围较左侧更大,响应值420-500 Ω·m,低视电阻率响应继续向x>0 m方向扩展至x=50 m处。对比实际模型,低视电阻率响应在横向分布上与阶梯状低阻异常体③对应性较好。综上所述,直流电阻率正演结果能有效反映地下异常的横向分布特征,但纵向分辨能力相对有限。
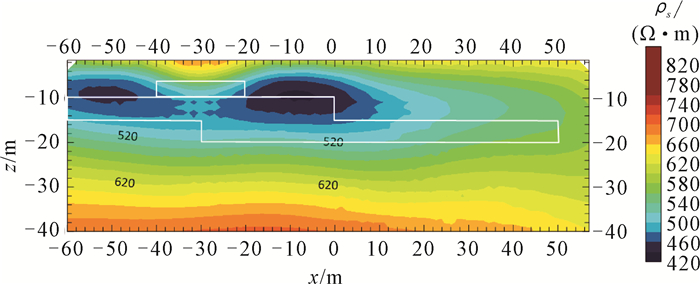
|
| 图 5 三维砂岩储层模型正演模拟剖面(y=0) Fig. 5 Forward modeling profile of 3D sandstone reservoir model (y=0) |
模型2:三维砂岩油水层模型
石油通常赋存在砂岩层中,并与水层及气层伴生分布。为研究传统水驱采油过程中水油分布的直流电阻率正演响应,设计一个三维砂岩背景下的水层和油层模型(图 6)。模型将砂岩作为背景(标记为⑤),内部包含编号为①-④的异常体,其参数设置参考内蒙古某地C类储层测井资料[25]。具体参数设置及异常体位置尺寸详见表 4、表 5,其中①与②为地下水体,③与④为油层。根据参数设置得到的理论地层电阻率Rt的y=0剖面,电阻率为5.9-150.0 Ω·m,其中①与②表现为低阻特征,③与④表现为高阻特征(图 7)。采用二极装置,在地表以原点为中心,沿x、y方向布设40×40的观测网,极距为5 m。正演计算时整个区域剖分单元数为911 406。不同异常体的组合可以反映阿尔奇参数的空间变化特征。图 8展示了不同异常体组合的正演响应结果,视电阻率为29.1-31.7 Ω·m。
|
| 图 6 三维砂岩油水层模型示意图 Fig. 6 Schematic diagram of 3D sandstone oil-water layer model |
| 序号 No. |
地质体类型 Geological body type |
比例系数 a |
岩性常数 b |
胶结指数 m |
饱和度指数 n |
孔隙度 φ |
含水饱和度 Sw |
地层水电阻率/(Ω·m) Rw/(Ω·m) |
地层电阻率/(Ω·m) Rt/(Ω·m) |
| ① | Groundwater | 1 | 1 | 1.596 | 2.647 | 0.05 | 1.00 | 0.050 | 5.962 3 |
| ② | Groundwater | 1 | 1 | 1.834 | 1.783 | 0.10 | 0.40 | 0.017 | 5.942 6 |
| ③ | Oil layer | 1 | 1 | 1.596 | 2.647 | 0.05 | 0.55 | 0.138 | 880.090 9 |
| ④ | Oil layer | 1 | 1 | 1.834 | 1.783 | 0.10 | 0.40 | 0.429 | 149.963 1 |
| ⑤ | Limestone | 1 | 1 | 2.119 | 1.364 | 0.16 | 0.20 | 0.069 | 30.110 2 |
| 序号 No. |
地质体类型 Geological body type |
x轴坐标/m x-axis coordinates/m |
y轴坐标/m y-axis coordinates/m |
z轴坐标/m z-axis coordinates/m |
| ① | Groundwater | -50--10 | -20-20 | -18--21 |
| ② | Groundwater | -20-80 | -30-30 | -63--77 |
| ③ | Oil layer | -50--10 | -20-20 | -27--47 |
| ④ | Oil layer | 10-50 | -20-20 | -26--42 |
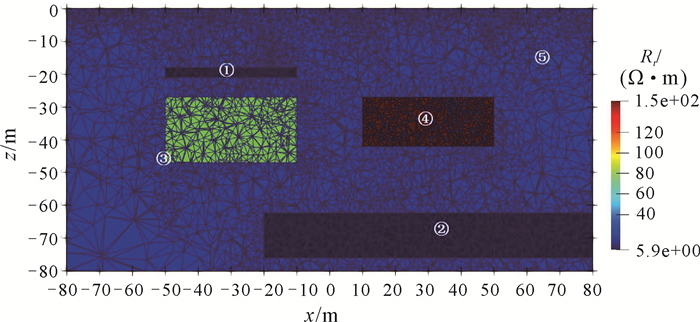
|
| 图 7 三维砂岩油水层模型地层电阻率Rt剖面(y=0) Fig. 7 Stratigraphic resistivity Rt profile of 3D sandstone oil-water layer model |
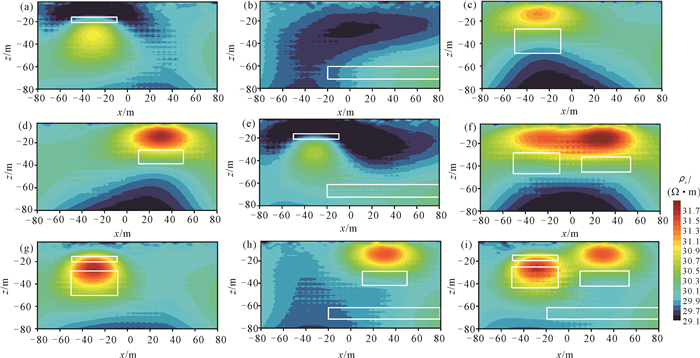
|
| (a) anomaly ① positive result; (b) anomaly ② positive result; (c) anomaly ③ positive result; (d) anomaly ④ positive result; (e) anomaly ①+② positive result; (f) anomaly ③+④ positive result; (g) anomaly ①+③ positive result; (h) anomaly ②+④ positive result; (i) anomaly ①+②+③+④ positive result. 图 8 三维砂岩油水层模型正演模拟剖面(y=0) Fig. 8 Forward modeling profile of 3D sandstone oil-water layer model (y=0) |
单异常体情况。图 8(a)仅含地下水异常体①,在x为-70 m至10 m,z为0 m至-20 m贴近地表处出现明显低视电阻率响应,响应范围大于实际异常体,但能较好反映实际异常体的水平位置。图 8(b)仅含地下水异常体②,有明显低视电阻率响应,响应自x为-60 m一直向x轴正方向和z轴深部延伸,异常形态清晰。图 8(c)仅含油层异常体③,表现为中高视电阻率响应,异常形态清晰(x为-60 m至0 m,z为-5 m至-30 m),能较好反映实际异常体的横向位置。图 8(d)仅含油层异常体④,表现为高视电阻率响应(x为0 m至60 m,z为-5 m至-25 m),同样能较好反映实际异常体的横向位置。
双异常体情况。当两个或多个异常体相邻时,其视电阻率响应会产生叠加效应。图 8(e)同时包含地下水低阻异常体①和②,左右两侧均出现低视电阻率响应,且右侧响应延伸至更深位置,准确反映了异常体的空间分布。图 8(f)同时包含油层高阻异常体③和④,在x为-50 m至50 m范围出现明显高视电阻率响应,且从左到右响应增大,右侧异常电阻率更高。高阻和低阻异常体及其组合在正演结果中形成鲜明对比,这有助于识别地下不同异常体的位置和物性。图 8(g)同时存在地下水低阻异常体①和油层高阻异常体③,正演结果仅呈现明显的高视电阻率响应(x为-50 m至-10 m,z为-10 m至-40 m),未见明显低视电阻率响应。对比图 8(a)、(c)、(g)可知,油层的高阻响应与地下水的低阻响应叠加后,导致含水饱和度降低、溶液电阻率增大,使原本的低阻响应转变为高阻响应。这一现象可用于推测地下水下方可能存在油层。图 8(h)同时存在地下水低阻异常体②和油层高阻异常体④,仅呈现单一高视电阻率响应(x为1 m至50 m,z为-5 m至-25 m)。对比图 8(b)、(d)、(h)发现,当油层下方溶液电阻率减小时,会削弱原有的高视电阻率响应,据此可推测油层下方可能存在地下水。
四异常体组合。正演结果[图 8(i)]综合了图 8(g)、(h)的特征,在两处区域出现明显高视电阻率响应,范围分别为x=-50 m至-10 m、z=-10 m至-40 m,x=1 m至-50 m、z=-5 m至-25 m。
4 结论本文通过对基于阿尔奇模型的三维直流电阻率正演研究,得出以下结论:
① 岩石孔隙度及孔隙流体性质会显著影响岩石电阻率,从而改变直流电阻率正演的视电阻率响应特征。基于阿尔奇公式建立的岩石电阻率与孔隙度、含水饱和度及溶液电阻率之间的关系模型,更适用于渗流场的电物性模拟研究。
② 针对砂岩储层模型与砂岩油水层模型,通过分析视电阻率响应变化特征,可有效推断油层或地下水层中含水饱和度与溶液电阻率等流体参数的变化规律,进而实现对渗流场物性分布的全面分析。
后续研究将在现有正演模型基础上,开展孔隙度、含水饱和度及溶液电阻率等参数的三维反演成像,以直接获取渗流场的流体性质空间分布特征。
| [1] |
TELFORD W M, GELDART L P, SHERIFF R E. Applied geophysics[M]. 2nd ed. Cambridge: Cambridge University Press, 1990.
|
| [2] |
REYNOLDS J M. An introduction to applied and environmental geophysics[J]. Preview, 2011(155): 33-40. |
| [3] |
ZHDANOV M S, KELLER G V. The geoelectrical methods in geophysical exploration[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1994, 31(4): 195. |
| [4] |
LOKE M H, ACWORTH I, DAHLIN T. A comparison of smooth and blocky inversion methods in 2D electrical imaging surveys[J]. Exploration Geophysics, 2003, 34(3): 182-187. DOI:10.1071/EG03182 |
| [5] |
HUBBARD S S, RUBIN Y. Hydrogeological parameter estimation using geophysical data: a review of selected techniques[J]. Journal of Contaminant Hydrology, 2000, 45(1/2): 3-34. |
| [6] |
BINLEY A, KEMNA A. DC resistivity and induced polarization methods[M]//BINLEY A, KEMNA A. Hydrogeophysics. Dordrecht: Springer Netherlands, 2005: 129-156.
|
| [7] |
CAI J C, WEI W, HU X Y, et al. Electrical conductivity models in saturated porous media: a review[J]. Earth-Science Reviews, 2017, 171: 419-433. DOI:10.1016/j.earscirev.2017.06.013 |
| [8] |
ARCHIE G E. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Transactions of the AIME, 1942, 146(1): 54-62. DOI:10.2118/942054-G |
| [9] |
WORTHINGTON P F. The uses and abuses of the archie equations, 1: the formation factor-porosity relationship[J]. Journal of Applied Geophysics, 1993, 30(3): 215-228. DOI:10.1016/0926-9851(93)90028-W |
| [10] |
SUN Z H, TORRES-VERDÍN C. The role of pore-shape and pore-space heterogeneity in non-archie behavior of resistivity index curves[J]. Journal of Geophysical Research: Solid Earth, 2022, 127(9): e2022JB024792. DOI:10.1029/2022JB024792 |
| [11] |
GUO Y H, SIMA L Q, WANG L, et al. Saturation evaluation of tight sandstone in the Dayi structure, West Sichuan Depression[J]. Frontiers in Earth Science, 2023, 11: 1223997. DOI:10.3389/feart.2023.1223997 |
| [12] |
XIAO L, SHI Y, LI G, et al. A method to predict the resistivity index for tight sandstone reservoirs from nuclear magnetic resonance data[J]. AAPG Bulletin, 2021, 105(5): 1009-1032. DOI:10.1306/05222018269 |
| [13] |
ZHDANOV M S. Geophysical inverse theory and regularization problems[M]//ZHDANOV M S. Methods in Geochemistry and Geophysics. Amsterdam: Elsevier, 2002.
|
| [14] |
LOKE M H. Electrical imaging surveys for environmental and engineering studies[C]. French Republic: IRIS Instruments, 2000.
|
| [15] |
HAN T, WEI Z, FU L Y. Cementation exponent as a geometric factor for the elastic properties of granular rocks[J]. Geophysics, 2020, 85(6): MR341-MR349. DOI:10.1190/geo2020-0250.1 |
| [16] |
KOWALSKY M B, FINSTERLE S, RUBIN Y. Estimating flow parameter distributions using ground-penetrating radar and hydrological measurements during transient flow in the vadose zone[J]. Advances in Water Resources, 2004, 27(6): 583-599. DOI:10.1016/j.advwatres.2004.03.003 |
| [17] |
REVIL A, CATHLES Ⅲ L M, LOSH S, et al. Electrical conductivity in shaly sands with geophysical applications[J]. Journal of Geophysical Research: Solid Earth, 1998, 103(B10): 23925-23936. DOI:10.1029/98JB02125 |
| [18] |
KNIGHT R J, ENDRES A L. Chapter 3: an introduction to rock physics principles for near-surface geophysics[M]//KNIGHT R J, ENDRES A L. Near-Surface Geophysics. Tulsa, Oklahoma: Society of Exploration Geophysicists, 2005: 31-70.
|
| [19] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.
|
| [20] |
冉冶, 王贵文, 王凯, 等. 四川安岳地区须家河组二段低渗储层不同孔隙结构岩电参数变化规律[J]. 地球物理学进展, 2015, 30(4): 1763-1771. |
| [21] |
郑庆林, 王钰森, 赵雨. 低孔隙度条件下阿尔奇含水饱和度解释模型改进[J]. 测井技术, 2006, 30(1): 57-59, 100. |
| [22] |
罗娜. 阿尔奇公式数值分析及其意义[J]. 石油学报, 2007, 28(1): 111-114. |
| [23] |
王伟, 赵娅, 李盼池, 等. 基于量子衍生涡流搜索的阿尔奇公式参数确定方法[J]. 地球物理学进展, 2022, 37(2): 678-683. |
| [24] |
张洁, 罗健, 夏瑜, 等. 阿尔奇公式的适用性分析及其拓展[J]. 地球物理学报, 2018, 61(1): 311-322. |
| [25] |
张明禄, 石玉江. 复杂孔隙结构砂岩储层岩电参数研究[J]. 石油物探, 2005, 44(1): 21-23, 28. |



