近年来，飞速发展的人工智能(Artificial Intelligence，AI)成为各学科发展的关键推动力，深度学习技术在AI领域中越来越重要。大语言模型(Large Language Model，LLM)是一种基于深度学习技术，以海量语料库为基础训练出的自然语言处理模型^[1-2]，如ChatGPT^[3-5]、Claude和DeepSeek等，均在AI领域产生了重要影响。神经网络作为实现深度学习的基础，通常是“黑箱”模型，无法揭示模型背后的潜在原理，降低了用户对系统的信任度。因此，探究数据之间的因果关系成为解决这个“黑箱”问题的关键路径。

因果关系是指自变量导致因变量发生变化的关系。在统计学中，当两个随机变量X和Y在统计上相关时，可能存在以下3种情况：①X→Y；②Y→X；③∃Z使得Z→X和Z→Y，其中Z为混杂变量。推断数据中因果关系的过程被称为因果发现，又称贝叶斯网络学习。因果网络是一种采用基于因果贝叶斯网络理论的有向无环图(Directed Acyclic Graph，DAG)来表示变量之间因果关系的图模型。在因果网络中，节点表示随机变量，有向边表示因果关系及其方向。因果网络是对多变量进行因果关系推断的关键工具，用于因果关系可视化^[6]。

基于观测数据的因果发现是一项具有挑战性的任务。现有的基于约束(Constraint-based)的因果发现算法易产生过多的冗余条件独立性测试，导致计算效率低。尽管无法完全避免所有冗余的条件独立性测试，但设计有效的分解策略可以尽可能减少冗余条件独立性测试，从而提高因果发现的效率。因此，本研究着眼于DAG的结构特性进行突破。DAG作为因果图模型的数学基础具有天然的模块化特性，本研究提出将图分割技术应用于因果分解，通过将复杂因果网络拆解为若干相对独立的子图模块，有效降低全局条件独立性测试的复杂度。在具体技术选择上，本研究采用K-means聚类进行因果分解。K-means聚类是一种经典的图分割技术，其分割效果好、泛化性强，能够适用于多种图结构^[7]。

综上，本研究将K-means聚类方法与条件独立性测试结合，提出一种新的因果分解方法(Causal decomposition method based on K-means clustering，CDKM)。CDKM通过无监督聚类将全局因果网络学习转化为多个子因果网络学习任务，相比递归型基于约束的方法，CDKM无需进行高阶条件独立性测试划分簇，避免了高阶条件独立性测试的使用，并显著减少了冗余测试，从而在因果发现中实现了更高的效率和更低的时间复杂度，为高维因果发现提供了高效解决方案。

1 相关工作 1.1 因果发现算法

基于约束的因果发现算法^[8-11]利用条件独立性测试方法推断数据中的因果关系，进而构建因果网络。因此，条件独立性测试是基于约束的方法的核心部分，决定了其效率和精度。其中，Peter-Clark (PC)算法作为一种经典方法，其首先基于观测变量集构建一个全连接无向图(骨架)，然后通过遍历式(条件)独立性测试对变量之间的边进行保留或删除，最后识别V-结构并通过一致性传播确定因果方向^[8]。PC算法能够与不同的条件独立性测试方法结合进行因果发现，但由于需要遍历式地进行条件独立性测试，会产生大量冗余测试，导致计算时间成本极高。Inductive Causation (IC)算法^[9]与PC算法的主要区别在于条件独立性测试和构建骨架的顺序。Fast Causal Inference (FCI)算法^[10]进一步扩展了处理隐变量和选择偏差的能力。Really Fast Causal Inference (RFCI)算法^[11]是FCI算法的变体，它在处理高维数据时更有效。

基于因果函数模型的算法^[12-15]的原理是假设因变量y和自变量x之间存在某种函数关系，进而推断因果关系。比如，若y=f(x)+ε_y，x=g(y)+ε_x，噪声项ε_y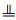x与y不独立，则x→y。线性非高斯无环模型(Linear Non-Gaussian Acyclic Model，LiNGAM)^[12]是一个经典的基于因果函数模型的方法，其可以从非时序连续数据中发现未观测到的线性混杂因素和扰动变量服从非高斯分布的完整因果网络，但LiNGAM的全局寻优思想会放大局部误差，导致其在高维因果网络上效果不够好。非线性加性噪声模型(Additive Noise Model，ANM)^[14]拓展了线性框架，通过判断回归后的残差与观测变量之间的独立性来进行因果方法的推断，提高了因果关系识别的能力。后非线性加性噪声模型(Post-Nonlinear Additive Noise Model，PNL)^[15]是ANM的一种广义模型，其原理与ANM相似。基于因果函数模型的因果发现方法主要采用ANM和PNL，这些方法可以处理不同类型的数据和问题，具有一定的灵活性，但也存在一定问题，如需要对模型进行假设、依赖数据的拟合和模型选择，以及难以处理多变量的情形等。

面对基于约束的算法会产生大量冗余的条件独立性测试的问题以及基于因果函数模型在高维因果网络上效果差的挑战，混合因果发现算法^[16-18]被提出。这种算法主要混合上述算法进行因果发现。Scalable cAusation Discovery Algorithm (SADA)^[16]通过在变量之间的稀疏概率图模型上找到切割点，将变量分成子集，也就是将原始的因果发现问题分解为多个子问题，然后在子问题上运行主流因果发现算法，如LiNGAM等，再通过组合所有子结果来重建完整的因果网络。SADA减少了一定的冗余条件独立性测试，提高了因果发现的效率和准确性，但因其需要通过穷举法最小化分离集，这意味着仍需要大量的条件独立性测试，导致计算时间复杂度较高。Causality Partitioning (CAPA)算法^[17]通过设计递归分解方法降低冗余条件独立性测试，同时采用基于回归的条件独立性测试处理线性非高斯加性噪声模型，CAPA算法能够显著减少不必要的条件独立性测试并有效区分Markov等价类。尽管CAPA算法比SADA更有效，但它在分解中需要进行高阶条件独立性测试，这影响了CAPA算法在高维因果发现任务中的效率和准确性。为了避免在分解中进行高阶条件独立性测试，Causal Decomposition based on Spectral Clustering (CDSC)算法^[18]通过构建原始变量集的Laplacian矩阵，利用谱聚类将原始变量集分解为多个子集，然后恢复每个子集的因果网络，最终合并这些子结果得到完整的因果网络。CDSC算法相对于其他因果分解方法的显著优势在于其使用简化的谱聚类，以保留子集的连通性，从而避免破坏分隔子集中的因果关系。但CDSC算法也有其缺点：当子集数量较多时，CDSC算法可能表现不佳。因为过多的子集数量可能导致子集内变量个数不足或变量在子集间的重叠度增加，影响精度和效率。

此外，基于评分的因果发现算法^[19-22]主要有贪婪等价搜索(Greedy Equivalence Search，GES)算法^[19]和快速贪婪等价搜索(Fast Greedy Equivalence Search，FGES)算法^[20]等。GES算法利用观测数据在DAG空间中搜索获取真实分布的完备图，但在有限样本的情况下计算复杂度较高。FGES算法是对GES算法的改进，采用启发式方法来减少搜索空间，但牺牲了一定的准确性。Non-combinatorial Optimization via Trace Exponential and Augmented lagRangian for Structure learning(NOTEARS)算法^[21]提供了一个新的因果发现视角，主要是将组合约束优化问题转化为实矩阵上纯连续优化问题，然后用数值优化算法进行求解。DAG structure learning with Graph Neural Networks (DAG-GNN)算法^[22]结合了深度学习和图神经网络，旨在从数据中学习DAG的结构。DAG-GNN能够捕获复杂的非线性关系，且可以自然地处理离散变量以及向量值变量，但其时间复杂度较高，难以处理高维因果发现问题。

1.2 K-means聚类

K-means聚类是一种基于距离度量的聚类算法，旨在将数据集划分为k个不同的簇，以使簇内的数据点尽可能相似，而簇间的数据点尽可能不相似。通过迭代更新簇的中心(质心)和将数据点分配到最近的簇中来优化簇的划分，直到满足停止迭代的条件。作为一种简单而有效的算法，K-means聚类可以将数据点分组成不同的簇，每个簇代表着一组具有相似特征的数据点。从因果发现的角度来看，这些簇可以被解释为潜在的因果成分或因果因素，它们在因果关系中可能起着相似的作用或具有相似的影响。因果分析通常涉及复杂的数据和概念，而K-means聚类的简单性使其成为解释和理解因果关系的理想选择。研究人员和决策者可以轻松理解该算法如何将数据分成不同的组，并且可以直观地解释结果。

K-means聚类首先从n个样本数据中随机选择k个对象作为初始质心，然后分别计算各样本到各质心的距离，将数据分配到距离最近的簇中，接着重新计算每个簇的中心点，并将新计算的质心作为每个簇的新中心点。这个过程不断地重复，直到质心不再改变时，停止并输出聚类结果^[23]。K-means聚类是一种广泛应用的无监督学习算法，已被证明在许多领域和应用中都具有良好的效果，如矿产资源勘探^[24]、市场细分^[25]、矿产远景预测^[26]和热环境区域化研究^[27]等。由于K-means聚类的稳定性、强泛化性及其优秀的聚类性能，本研究将其应用于因果分解中，为因果分析提供了新的思路和方法。

2 基于K-means聚类的因果分解算法 2.1 CDKM的框架

CDKM (图 1)的输入包括原始变量集V、因果发现算法Ag(本研究采用PC算法)和簇的个数k。CDKM首先利用K-means聚类将原始变量集V分割成k个簇$\left\{V_i\right\}_{i=1}^k$，接着在V_i中加入其他簇中相关距离最小的q个节点，得到更新后的k个簇$\left\{V_i\right\}_{i=1}^k$，增加节点的操作保证了每个簇之间都存在交集，这一步是为了后面的合并操作。紧接着是在每个簇V_i上利用因果发现算法Ag进行因果发现，得到各个子因果网络G_i，最后将每一个子因果网络G_i合并得到一个完整的因果网络G。

2.2 CDKM因果分解策略

在因果分解中，为了避免冗余的条件独立性测试，本研究利用K-means聚类对原始变量集V进行分解。K-means聚类通过计算数据点之间的距离来划分数据集。常用的欧式距离与因果性关系不大，相关性与因果性存在一定的关系，因此，本研究选用相关距离[式(1)]进行聚类。

$ d\left(v_i, v_j\right)=1-\frac{\operatorname{cov}\left(v_i, v_j\right)}{\sqrt{\operatorname{cov}\left(v_i, v_i\right) \operatorname{cov}\left(v_j, v_j\right)}}, $

(1)

其中，v_i，v_j是两个变量，cov(v_i，v_j)表示v_i和v_j的协方差，cov(v_i，v_i)为v_i的方差，cov(v_j，v_j)为v_j的方差。

CDKM的分解过程如算法1所示。

算法1  CDKM因果分解策略

输入: 原始变量集V，簇的个数k，增加的节点数q

输出: k个簇$\left\{V_i\right\}_{i=1}^k$

1.   初始化：$\left\{V_i=\phi\right\} k_{i=1}$

2.   对$\forall c_i \in\left\{v_1, v_2, \cdots, v_n\right\} \text {, 令 } V_i=\left\{c_i\right\}, i=1 , 2, \cdots, k$

3.   Repeat

4.     对$\forall v_j \in V \backslash\left\{c_1, c_2, \cdots, c_k\right\}$，计算v_j与c_i的相关距离d(c_i，v_j)=1-ρ(c_i，v_j)，其中$\begin{aligned} \rho\left(c_i, v_j\right)= \frac{\operatorname{cov}\left(c_i, v_j\right)}{\sqrt{\operatorname{cov}\left(c_i, c_i\right) \operatorname{cov}\left(v_j, v_j\right)}}, i=1, 2, \cdots, k \end{aligned}$

5.     If $d\left(c_i, v_j\right)=\min \left\{d\left(c_i, v_j\right)\right\}_{i=1}^k$ then

6.         将v_j添加到V_i中

7.         End if

8.         计算新的聚类中心$c_i^{\prime}=\frac{1}{\left|V_i\right|} \sum_{v_j \in V_i}{v_j}$，i=1，2，…，k，其中V_i表示第i个簇内的所有数据点集合

9.         If c_i^′≠c_i then

10.             令c_i=c_i^′

11.         End if

12.     until c_i=c_i^′

13.     对$\forall v_j \in V \backslash V_i=\left\{v_{i 1}, v_{i 2}, \cdots, v_{i p_i}\right\}$，p_i=$\left|V_i\right|, i=1, 2, \cdots, k$，计算v_j与v_it的相关距离d_i(v_it，v_j)(t=1，2，…，p_i)，得到相关距离矩阵D_i=(d_i(v_it，v_j))_pi×(n-pi)

14.     令$d_i=\left(d_i\left(v_{i j_1}, v_{j_1}\right), d_i\left(v_{i j_2}, v_{j_2}\right), \cdots, \right.\left.d_i\left(v_{i j_{n-p_i}}, v_{j_{n-p_i}}\right)\right)^{\mathrm{T}}$代表D_i中第m列的最小值

15.     在d_i中找到前q个最小值，令

$ \begin{aligned} & d_i^{\min }=\left(d_i\left(v_{i j_1^{\prime}}, v_{j_1^{\prime}}^{\prime}\right), d_i\left(v_{i j_2^{\prime}}, v_{j_2^{\prime}}\right), \cdots, d_i\left(v_{i j_q^{\prime}}, \right.\right. \\ & \left.\left.v_{j_q^{\prime}}^{\prime}\right)\right)^{\mathrm{T}} \end{aligned} $

16.     将节点v_j1^′，v_j2^′，…，v_jq^′添加到V_i

17.     Return更新后的k个簇$\left\{V_i\right\}_{i=1}^k$

2.3 子网络合并

对原始变量集V进行因果分解后，CDKM选用指定的因果发现算法Ag在每个簇V_i上进行因果发现，得到各个簇对应的子因果网络$\left\{G_i\right\}_{i=1}^k$，再将各个子因果网络$\left\{G_i\right\}_{i=1}^k$合并得到一个完整的因果网络G。

由于K-means聚类划分的簇之间不存在交集，无法发现不同簇节点间的因果关系，即无法建立子因果网络之间的因果关系；故在CDKM的分解部分中，在进行K-means聚类后，本研究为每个簇添加了其他簇中与其相关距离最小的q个节点，保证了不同簇之间存在重叠部分，使因果发现算法Ag能够恢复不同簇之间的因果关系。根据文献[18]，取q=2，这既可以防止簇中节点数目不足，导致在其上难以进行因果发现，也可以避免簇中节点数目过多进而影响算法的效率。

针对每个簇的因果发现和合并子因果网络的问题，本研究不失一般性地选用PC算法来作为因果发现算法。CDKM在确定因果方向时有两种操作：一是通过条件独立性测试检测到的对撞结构来确定因果方向；二是因条件独立性测试无法区分Markov等价类，即无法区分v₁→v₂→v₃、v₁←v₂←v₃和v₁←v₂→v₃，故在区分Markov等价类时，通过检验独立变量z是否独立于残差v₁-E(v₁|Z)和v₃-E(v₃|Z)来确定因果方向。

子因果网络之间存在重叠部分，使得它们之间可能会发生一些冲突，尤其是在处理含有大量变量的数据集时。在实践中，可能出现在G_i和G_j中分别推断出不同的因果方向的冲突。比如在G_i中的因果方向是v_i→v_j，而在G_j中的因果方向是v_i←v_j。一般而言，这种冲突取决于DAG对因果网络的假设^[20]。针对这类冲突，CDKM首先用两个变量的(条件)独立性测试计算出相应的显著性数值(简称SV)，然后选择SV较高的边作为最终结果。比如，若满足SV_vi→vj=P((v_i-E(v_i|Z))v_j)>SV_vi←vj=P((v_j-E(v_j|Z))v_i)，则CDKM会选择v_i→v_j作为v_i和v_j的最终因果方向。

总的来说，CDKM的合并操作可以归结为4步：首先，根据原始变量集V构建无边图G′；其次，将各G_i的因果边都添加到G′中；接着，对于G′出现的冲突因果边，删除SV更低的因果边，并更新G′；最后，令G=G′，从而得到完整因果网络G。算法2为CDKM合并子因果网络的伪代码。

算法2  合并子因果网络

输入: 原始变量集V，子因果网络$\left\{G_i\right\}_{i=1}^k$

输出: 完整因果网络G

1.     根据V构建无边图G′。

2.     对$\forall v_i \rightarrow v_j \in G_i, i=1, 2, \cdots, k, $令$v_i \rightarrow v_j \in G^{\prime}$。

3.     若v_i→v_j和v_i←v_j同时存在G′中，且SV_vi→vj≥SV_vi←vj，则删除v_i←v_j，否则删除v_i→v_j，更新G′。

4.     令G=G′，从而得到完整因果网络G。

2.4 时间复杂度

条件独立性测试占据了因果发现算法95%以上的时间^[8]。因此，CDKM的时间复杂度主要由K-means聚类和在簇内进行因果发现的时间复杂度组成。

命题1   令原始变量集V={v₁，v₂，…，v_n}，CDKM将V划分为k个簇{V_i}_i=1^k，其中每个簇的大小为|V_i|，设：p_max=max(|V₁|，|V₂|，…，|V_k|)，d为变量的维度，t为K-means聚类的迭代次数，m为条件独立性测试的时间复杂度，已知K-means聚类的时间复杂度为Ο(kndt)，PC算法的时间复杂度为Ο(mn²2^n-2)，若CDKM在每个簇内使用PC算法进行因果发现，则当n较大时，CDKM的时间复杂度为$O\left(k m p_{\max }^2 2^{p_{\max }^{-2}}\right)$，且满足$O\left(k m p_{\max }^2 2^{p_{\max }^{-2}}\right) \ll O\left(m n^2 2^{n-2}\right)$。

证明   因为CDKM在每个簇内使用PC算法进行因果发现，所以CDKM在每个簇上进行因果发现的时间复杂度为$O\left(m\left|V_i\right|^2 2^{\left|V_i\right|-2}\right)$，故在k个簇上进行因果发现的总时间复杂度上界为$O\left(k m p_{\max }^2 2^{p_{\max }}{ }^{-2}\right)$。又因为K-means聚类的时间复杂度为Ο(kndt)，所以CDKM的时间复杂度上界为$O(k n d t+\left.k m p_{\max }^2 2^{p_{\max }^{-2}}\right)$。当n较大时，p_max通常远小于n，但$2^{p_{\max }}{ }^{-2}$仍然是一个指数级增长的项，远快于多项式kndt的增长，即$O(k n d t) \ll O\left(k m p_{\max }^2 2^{p_{\max }^{-2}}\right)$，此时CDKM的时间复杂度主要取决于条件独立性测试的时间复杂度，因此CDKM的时间复杂度为$O\left(k m p_{\max }^2 2^{p_{\max }^{-2}}\right)$，由于$p_{\max } \; \ll \; n$，故$O\left(k m p_{\max }^2 2_{p_{\max }}^{-2}\right) \ll O\left(m n^2 2^{n-2}\right)$。

命题1说明了在高维情形下，CDKM相比于PC算法具有更低的时间复杂度，因果发现的速度更快，因此具有可行性。

3 实验与结果分析

为了验证和分析本研究提出的算法的有效性，本研究在8个现实因果网络上做了算法性能评估和对比实验。具体来说，一是使用不同数量的簇个数k对这8个数据集评价此算法的性能；二是本研究将CDKM与CDSC^[18]、PC^[8]、SADA^[16]这3个性能优越的因果发现算法进行比较，其中和PC算法的对比是关于CDKM分解操作的消融实验。

3.1 实验设置

实验的软件环境为Windows 11操作系统和Matlab2022a，硬件环境配备AMD Ryzen 5 5600H with Radeon Graphics处理器与16 GB内存。参数实验和对比实验均设置每个数据的样本容量为600，每个实验运行25次，取25次实验的平均值作为最终结果。

3.1.1 数据集

在这组实验中，本研究选用Sachs、Water、Insurance、Alarm、Barley、Hailfinder、Win95pts和Andes这8个现实世界的因果网络进行实验。表 1给出了这些因果网络的具体信息。它们涵盖了生物信息学(Sachs)、保险评估(Insurance)、环境保护(Water)、医学(Alarm)、农业(Barley)、天气预报(Hailfinder)和系统故障排障(Win95pts、Andes)等方面的应用。

因为这些原始变量集是因果网络而不是具体的数据，故在进行分解之前，需先将因果网络生成数据。因为在现实世界中大规模的具有真值的因果发现问题不常见，而大多数的真实数据满足ANM^[28]：

$ v_i=\sum\limits_{v_j \in P a\left(v_i\right)} \omega_{i j} v_j+\varepsilon_i, $

(2)

其中，Pa(v_i)为v_i的父节点集合，ε_i为非高斯噪声项，ω_ij是父节点v_j对v_i的权重，生成数据的过程满足ω_ijPa(v_i)=1，var(ε_i)=1;故本研究选用ANM生成数据，数据生成过程参考文献[16]。

3.1.2 评估指标

本研究选用召回率(R)、精准率(P)和F1分数(F1)这3个指标评估CDKM的准确性，选用运行时间来评估算法的效率。

召回率衡量的是在实际存在因果关系的样本中，算法正确识别出存在因果关系的样本所占的比例，即

$ R=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}, $

(3)

其中，TP (True Positives)为识别出存在因果关系且实际也存在因果关系的样本数，FN (False Negative)为识别出不存在在因果关系但实际存在因果关系的样本数。

精准率衡量的是在算法识别为存在因果关系的样本中，实际存在因果关系的样本所占的比例，即

$ P=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}, $

(4)

其中，FP (False Positive)为识别出存在因果关系但实际不存在因果关系的样本数，F1分数是召回率和精准率的调和平均数，旨在综合考虑二者性能，使两者同时达到较高水平。其公式如下：

$ F 1=\frac{2 \times R \times P}{R+P} 。$

(5)

3.2 参数实验

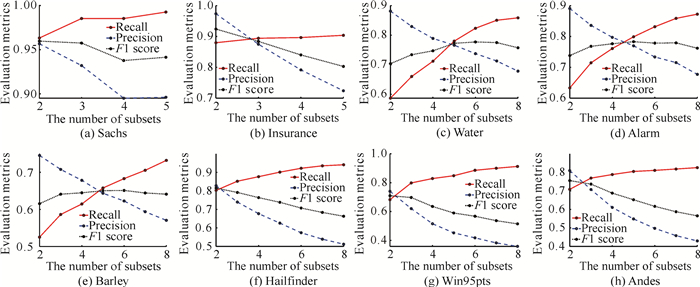
本节研究簇个数k对CDKM准确性和效率的影响，以及找到使得CDKM在各个数据集上表现最佳的k值。在这组实验中，设置k={2，3，…，8}。需要注意的是CDKM在Sachs和Insurance上的值不能设置太大，因为随着k值的增大，簇变得越来越相似，不同簇中的许多节点变得相同。

图 2说明了簇个数k对CDKM算法准确性的影响。CDKM在每个数据集上的召回率随着k值的增加而增大，即CDKM成功发现因果关系的比例在增大。相反，精准率随着k值的增大而减小，说明CDKM正确发现因果关系的可靠性在降低。这可能是当划分的簇个数过多时，簇内变量较少，可供参考的背景信息减少，从而增加了因果推断错误的风险。此外，CDKM在Sachs、Insurance、Hailfinder、Win95pts和Andes上的F1分数随着k值的增大而减小。这说明随着k值的增加，CDKM在因果发现任务中准确识别真实因果关系和避免错误推断的能力逐渐下降，导致其在整体因果发现效果上表现不佳。而CDKM在Water、Alarm和Barley上随着k值的增大F1分数表现出先升高后降低的趋势。这表明在这些数据集上，存在一个较优的簇个数范围，使得CDKM具备更强的能力去精准识别出数据中的因果关系，尽可能减少误判和漏判。不过，一旦簇个数超出这个范围，CDKM在因果发现任务中准确挖掘因果关联、有效区分真实因果与虚假关联的能力就会减弱，进而导致算法整体性能下滑。

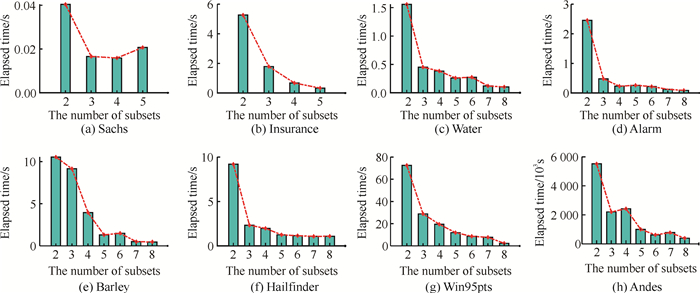
根据图 3，CDKM对Sachs、Insurance、Water、Alarm、Barley、Hailfinder、Win95pts和Andes这8个数据集的效率通常随着k值的增大而提高，这说明划分的簇个数越多，越能提升CDKM的效率，因为这样能够减少CDKM原本要执行的冗余条件独立性测试。

基于图 2和图 3，本研究总结了CDKM在Sachs、Insurance、Water、Alarm、Barley、Hailfinder、Win95pts和Andes这8个数据集上表现最佳的k值(表 2)。

最佳簇个数的选择通常要在准确性和效率之间进行权衡，当前最先进的递归方法在效率方面表现出色，但本研究更倾向于准确性而不是效率，特别考虑到算法的可接受性。由表 2可知，划分数据集的最优k值大多等于2。这表明划分的簇个数过多可能导致簇无法保持稀疏性，从而影响CDKM的准确性。因此，本研究更注重保持因果网络的准确性而不过度追求簇的数量，以确保结果的可靠性。

综上，不同的簇个数k会对CDKM的性能产生影响，且随着k值的增加，CDKM在每个因果网络上的召回率变大，精准率变小，运行时间变短，CDKM在Insurance、Hailfinder、Win95pts和Andes上的F1分数减小，而在Sachs、Water、Alarm和Barley这4个数据集上先变大后减小。这是因为随着划分簇个数的增加，使用条件独立性测试的次数减少，从而使CDKM的速度加快。

3.3 对比实验

本节将CDKM与SADA、PC、CDSC这3个性能优越的因果发现算法进行比较，主要比较这些算法在Sachs、Insurance、Water、Alarm、Barley、Hailfinder、Win95pts和Andes这8个数据集的召回率、精准率、F1分数和运行时间上的差异。CDKM的k值选用表 2中的最优k值。对比实验结果如表 3所示，其中召回率、精准率、F1分数以“平均值±标准差”的形式给出。

由表 3可以看出，在召回率方面，CDKM在Insurance数据集上表现优于其他3个算法，而在Sachs、Water、Alarm、Barley和Hailfinder数据集上略逊于PC算法。这表明CDKM在正确识别因果边上的能力仅次于PC算法，这是因为CDKM没有遍历式地对观测变量进行条件独立性测试，而PC算法采用了全局遍历条件独立性测试。CDKM在整体上略优于CDSC算法，这是因为K-means聚类在效果上较谱聚类更为出色，簇的划分更为合理，从而提高了正确识别因果关系的数量。相比之下，SADA在召回率上表现不佳，可能是由于在进行分割时切割点选择不当，破坏了图的连通性，导致一些因果关系被忽略。

从精准率来看，PC算法在这8个数据集上均表现出最优性能，CDKM整体上表现为次优。由于条件独立性测试具有较高的准确性，PC算法在精准率方面表现尤为突出。CDKM低于PC算法，可能是因为对数据进行划分后，簇内变量较少，可供参考的背景信息减少，从而增加了因果推断错误的风险。CDSC算法相较于CDKM略差，可能是由于其簇划分质量稍逊，导致条件独立性测试可能标记不正确的因果关系。而SADA在精准率上不足，可能是因为其对稀疏性约束的假设限制了其捕获复杂因果关系的能力。

最后，在综合考虑召回率和精准率的F1分数上，PC算法在Sachs、Water、Alarm、Barley、Hailfinder、Win95pts和Andes这7个数据集上均表现最优，证明了其在综合性能上的优势性。而在Insurance上，CDKM取得了最优表现。尽管CDKM在F1分数上略逊于PC算法，但其在与CDSC算法和SADA的比较中仍表现较好，这证明了CDKM在识别因果关系方面具有一定的准确性。CDKM在F1分数上的不足，可能源于其分割策略导致不同簇节点间的因果关系被遗漏或因果方向判断错误。

在Alarm和Andes上运行时间最少的是CDKM，在Barley和Win95pts上运行时间最少的是CDSC算法，在Insurance和Hailfinder上运行时间最少的是SADA，整体上看CDKM、CDSC算法和SADA的运行时间较少，而PC算法的运行时间高出很多，这是因为PC算法需遍历式地对观测变量进行条件独立性测试来找到所有条件集，故消耗时间多。SADA在Andes上的运行时间剧增，是因为随着数据维度的增加，用于分解的高阶条件独立性测试会大大增加SADA的运行时间。CDKM在高维上具有良好的时间表现，是因为K-means聚类在最佳簇个数k下划分子集，避免了分解时进行高阶条件独立性测试，大大提高了时间效率。

为了检验CDKM和PC算法在各数据集上的召回率、精准率和F1分数有无显著性差异，利用配对样本Wilcoxon符号秩检验进行检验，假设CDKM和PC算法在各数据集上的召回率、精准率和F1分数没有显著性差异，检验结果如表 4所示。

从表 4可以看出，计算出的P值均大于0.05，故在5%的显著性水平下无法拒绝原假设，证明CDKM和PC算法在各数据集上的召回率、精准率和F1分数没有显著性差异，表明CDKM能够保证准确性。尽管CDKM的召回率、精准率和F1分数低于PC算法，但不存在显著性差异，且CDKM的时间效率远高于PC算法，说明CDKM的方法是有效的。

4 结论

本研究将K-means聚类方法与条件独立性测试结合，提出了一种基于K-means聚类的因果分解方法CDKM。CDKM通过K-means聚类将原始因果发现问题划分为多个子因果发现问题，避免了高阶条件独立性测试，并减少了冗余测试。相比递归型基于约束的方法，CDKM能够根据需求灵活分割变量集。在8个现实数据集上的实验结果表明，CDKM可以极大地加速因果发现，降低时间复杂度，且精准度优于基线模型。

然而，CDKM也有其不足之处。CDKM利用K-means聚类对原始变量集进行分割，破坏了因果充分性，无法正确地识别出关键原因变量，从而导致精准率下降。此外，K-means对初始聚类中心的选择敏感，不同的初始中心会导致不同的聚类结果，聚类结果不稳定，可能会导致因果发现结果的不确定性，或者对数据中隐藏的因果关系产生误导。

未来，将聚类方法与条件独立性测试相结合，深入探究因果分割技术，有望解决因果分解领域固有的局限。通过改进初始聚类中心的选择，如采用K-means++方法^[29]，可以让聚类结果更具稳定性，但如何让划分子集保留完整的局部因果关系是一项艰巨的挑战。同时，针对缺失、嘈杂和动态的现实世界的数据，提出适用的因果发现方法至关重要，这是未来的研究重点之一。