在数学领域中, 优化是指在给定问题的解集合中依据合适的方法(如牛顿法、单纯形法等)来搜寻全局最优解或近似最优解。然而, 由于在实际工程问题中普遍存在测量误差、外部干扰等不规律性因素, 以及系统的复杂性, 这些因素导致理论模型与实际之间存在较大误差, 从而使得传统基于梯度的优化算法[1]难以准确地找到全局最优解。因此, 基于群体智能的元启发式优化算法开始被人们所关注, 其通过模拟自然界中各类生物的复杂行为进行迭代寻优。近些年已被成功应用于图像处理[2]、电力系统[3]、机器学习[4]、工程设计[5]等领域。
正余弦算法(Sine Cosine Algorithm, SCA)是一种模拟正余弦函数来回振荡行为的群体智能优化算法[6]。和其他群体智能优化算法一样, SCA在搜索全局最优时经过两个阶段: 全局探测和局部挖掘。因为SCA具有结构简单、实现方便等优点, 同时其随机参数可以很好地平衡算法的探索和开发能力, 所以被广泛应用于解决各类工程应用问题, 例如经济排放调度[7]、路径规划[8]、文本特征选择[9]、光纤放大器的设计[10]等。Rizk-Allah等[11]对SCA的最新研究进展进行了全面综述, 并将SCA变体算法的改进思路大致分为以下3类。①种群多样性的加强。一般来说, SCA的随机初始化方式会因群体分布不均, 从而降低种群多样性,最终导致局部收敛甚至搜索停滞。为算法迭代提供一个较优的初始种群位置, 可以显著提高算法的搜索能力, 因此各种混沌学理论被用于替代随机方法, 如Singer映射[12]和Logistic映射[13]。此外, Feng等[14]通过对立学习生成对立解来扩大搜索范围, 避免算法陷入局部最优。王华秋等[15]在初始化阶段引入拉丁超立方体, 通过均匀划分搜索空间并采样, 使初始种群分布更均匀。Chen等[16]在SCA中引入正交学习, 扩大了算法的邻域搜索能力。②位置更新方程的设计。在SCA中, 种群位置的更新机制主要依赖正弦和余弦函数, 通过二者在进化过程中平衡探索与开发, 从而提升算法收敛性能。但近年来随着人工智能、大数据、物联网、5G、元宇宙的发展, 优化问题正在向大规模、多任务、多目标、多参数等方向演化, 给SCA带来了巨大挑战。如何避免算法在面对复杂优化问题时陷入局部最优成为了该领域重点关注的研究热点。Sindhu等[17]提出一种具有精英策略引导最佳解机制的正余弦算法用于特征选择, 成功提升了算法的全局搜索能力。Raut等[18]为了最大限度提高种群的搜索效率, 在更新机制中充分结合莱维飞行策略并将其用于解决网络配置和分布式发电机同时分配的问题。但是, 这种单一改进策略在许多问题中依然很难发挥算法的全部性能。因此, Liu等[19]分别设计了增强的精英领导力、交叉和最优选择结合以及逐维更新这3种新颖策略来修正SCA。③与先进算法的混合。两种或两种以上算法的更新机制组合可以有效增强原始SCA的搜索能力, Issa等[20]提出粒子群优化与SCA的混合算法, 通过共享两种算法的进化机制, 在生物局部序列对比上得到成功应用。Gupta等[21]结合差分进化与SCA来解决多维背包问题。Ansari等[22]提出将海豚群优化算法与SCA混合来研究视频内容自动检测。
尽管SCA已经在各个方面取得了巨大进展, 但是仍需要进一步提升其性能。因此, 本文提出一种融合疯狂秃鹰搜索的混沌正余弦算法(Chaotic Sine Cosine Algorithm based on Crazy Bald-eagle Search, CSCA-CBS)。为了验证CSCA-CBS的优化能力, 在15个基准函数上进行测试, 并使用非参数检验方法进行统计学分析, 然后通过求解土壤水分特征曲线参数反演问题, 进一步验证CSCA-CBS的实用性和有效性。
为了优化SCA, 本文提出3种改进策略: ①引入Logistic-Tent映射策略初始化种群, 融合Tent映射的均匀分布特性和Logistic映射的非线性特征, 提高初始种群多样性; ②采用“疯狂算子”扰动种群, 增强全局探索能力并避免陷入局部最优, 同时将秃鹰搜索策略与“疯狂算子”相融合, 进一步提升全局探索性能和效率; ③提出逐维反向变异策略, 通过反向扩大搜索空间, 允许种群在陷入局部最优时接受部分较差解以跳出局部最优, 并增强变异策略效率, 减少维度间干扰, 从而提升算法寻优能力。
1 基本正余弦算法考虑一个n维最小化问题:
| $ \min\limits_{x_i \in \Omega} f\left(x_1, x_2, \cdots, x_n\right), $ | (1) |
其中, xi为决策变量, Ω={lbi≤xi≤ubi, i=1, 2, …, n}是解空间。ubi和lbi分别为xi在解空间中的上、下边界。
SCA利用正余弦函数构建描述全局探索与局部开发的数学模型:
| $ \begin{array}{l} \;\;\;\;\;\;x_{i, j}^{i t e r+1}= \\ \left\{\begin{array}{l} x_{i, j}^{i t e r}+r_1 \times \sin \left(r_2\right) \times\left|r_3 \times p_{\text {best }, j}^{i t e r}-x_{i, j}^{i t e r}\right|, \\ \;\;\;\;\;r_4<0.5 \\ x_{i, j}^{i t e r}+r_1 \times \cos \left(r_2\right) \times\left|r_3 \times p_{\text {best }, j}^{i t e r}-x_{i, j}^{i t e r}\right|, \mathrm{else} \end{array}\right., \end{array} $ | (2) |
| $ r_1=a-a \times \frac{i t e r}{M a x\_{i t e r}}, $ | (3) |
式中, xi, jiter和pbest, jiter分别表示个体i和最优个体在第j维经过第iter次迭代后的种群位置。r1为探索(r1>1)与挖掘(r1<1)的控制参数, r2、r3和r4分别是[0, 2π]、[0, 2]和[0, 1]间的随机数, 常数a=2, Max_iter为最大迭代次数。
令个体上一代的最佳位置x*iter=argminf(xi, jiter), 且y*iter+1=argminf(xi, jiter+1), 通过贪心选择策略来获取当前全局最优位置x*iter+1, 即:
| $ x_*^{i t e r+1}=\left\{\begin{array}{l} y_*^{i t e r+1}, f\left(y_*^{i t e r+1}\right)<f\left(x_*^{i t e r}\right) \\ x_*^{i t e r}, \text { otherwise } \end{array} 。\right. $ | (4) |
SCA中的随机初始解方式会导致种群分布不均匀, 多样性降低, 进而限制算法的优化能力。混沌学理论凭借其独特的遍历性和规律性, 与SCA的初始化需求高度契合, 有助于种群更充分地探索整个搜索空间。目前使用广泛的混沌映射主要是Logistic映射[23]和Tent映射[24], 且大量文献已证明这两种方法在种群分布上优于随机函数[25-26]。Logistic映射[图 1(a)]和Tent映射[图 1(b)]的直方图均反映了两种映射不同的局限性,因此它们难以很好地指导种群的高效探索。值得注意的是,Logistic映射使[0.0, 0.1]和[0.9, 1.0]的种群分布密集,而Tent映射可以大致认为是在整个搜索空间具有分布,但分布均匀度稍差。

|
| 图 1 混沌映射的分布情况对比图 Fig. 1 Comparison of chaotic mapping |
Logistic映射和Tent映射的公式分别如式(5)和式(6)所示:
| $ z_{n+1}=\mu z_n\left(1-z_n\right), $ | (5) |
| $ z_{n+1}=\left\{\begin{array}{l} k z_n / 2, z_n<0.5 \\ k\left(1-z_n\right) / 2, z_n \geqslant 0.5 \end{array}\right., $ | (6) |
其中,μ和k均为控制参数, μ∈[3.57, 4.00][27], k∈[2, 4], zn为状态值。
基于此, 本文将两种映射结合, 提出一种Logistic-Tent映射策略用于初始化种群, Logistic-Tent映射直方图[图 1(c)]既整体均匀, 又在某些区域有起伏, 能更好地兼顾全局和局部搜索, 从而提升算法的综合性能。具体公式如下:
| $ \begin{array}{l} \;\;\;\;\;\;z_{n+1}= \\ \left\{\begin{array}{l} \left(r z_n\left(1-z_n\right)+(4-r) z_n / 2\right) \text{ mod } 1, z_n<0.5 \\ \left(r z_n\left(1-z_n\right)+(4-r)\left(1-z_n\right) / 2\right) \text{ mod } 1, \text { else } \end{array}, \right. \end{array} $ | (7) |
其中, r为混沌参数, r∈(0, 4][27]。接着, 将产生的混沌序列值映射到搜索空间:
| $ x_{i, j}=l b_j+z_{i, j} \cdot\left(u b_j-l b_j\right), $ | (8) |
其中, xi, j表示第i个个体在第j维的位置, zi, j是第i个个体的状态,ubj和lbj为xi取值的上、下边界。
2.2 疯狂秃鹰搜索策略SCA由于缺乏对历史信息与当前信息的整合, 仅依赖正余弦函数进行交替迭代寻优难以平衡收敛速度与寻优精度, 在诸多复杂优化问题中表现乏力。作为一种新型的全局优化算法, 秃鹰搜索算法[28]会充分根据历史迭代中的最佳信息和平均化信息来选择当前最佳搜索区域, 其搜索行为如式(9)所示:
| $ x_{i, j}^{i t e r+1}=x_{\text {best }, j}^{i t e r}+\alpha \times r \times\left(x_{\text {mean }}^{i t e r}-x_{i, j}^{i t e r}\right), $ | (9) |
其中, xbest, jiter是秃鹰搜索当前的最佳位置, xmeaniter是搜索前后的平均位置, α∈[1.5, 2.0]表示控制秃鹰搜索范围的参数[28], r∈(0, 1)是伪随机数。
虽然加入秃鹰搜索策略能够有效弥补SCA的不足, 并使得种群一直朝着最优区域的方向进行移动, 但难免会出现种群的聚集现象, 从而大大降低种群多样性, 增加陷入局部最优的概率。于是, 本文引入疯狂算子对种群进行微小扰动, 使得种群可以在充分搜索的过程中维持其多样性。综上, 融合疯狂秃鹰搜索策略的SCA更新公式如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;x_{i, j}^{i t e r+1}= \\ \left\{\begin{array}{l} \tilde{x}_{\text {best }, j}^{i t e r}+r_1 \times \sin \left(r_2\right) \times\left|r_3 \times x_{\text {mean }}^{i t e r}-x_{i, j}^{i t e r}\right|, \\ \;\;\;\;\;\;\;r_4<0.5 \\ \tilde{x}_{\text {best }, j}^{i t e r}+r_1 \times \cos \left(r_2\right) \times\left|r_3 \times x_{\text {mean }}^{i t e r}-x_{i, j}^{i t e r}\right|, \text { else } \end{array}, \right. \end{array} $ | (10) |
| $ \begin{aligned} & \quad \tilde{x}_{\text {best }, j}^{iter}=x_{\text {best }, j}^{iter} \times\left(1+P\left(c_4\right) \times \operatorname{sign}\left(c_4\right)\right. \\ & \left.x_{\text {craziness }}\right) \end{aligned} $ | (11) |
其中,
| $ P\left(c_4\right)=\left\{\begin{array}{l} 1, c_4 \leqslant P_c \\ 0, \text { otherwise } \end{array}, \right. $ | (12) |
| $ \operatorname{sign}\left(c_4\right)=\left\{\begin{array}{l} -1, c_4 \geqslant 0.5 \\ 1, \text { otherwise } \end{array}, \right. $ | (13) |
其中, Pc表示疯狂概率,c4为一个随机数。
2.3 逐维反向柯西变异与高斯函数相比, 柯西函数能够在短时间内对种群进行大幅度扰动, 使算法在陷入局部最优区域时快速逃离[29]。然而, 柯西变异缺乏明确的逃离方向, 导致种群逃离行为杂乱无章, 甚至可能抛弃处于较优区域的个体。针对这个问题, 本文引入透镜成像反向学习策略将搜索空间范围进行反向扩大, 一是使得种群在陷入局部最优时能够适当接受个别较差的解作为踏板跳出局部最优区域;二是能够在柯西扰动时指明一条明确的逃离方向。另外, 为了进一步提高变异策略的效率以及维度之间的相互干扰, 通过逐维变异可以更好地得到变异解。整个变异过程的数学表达式如下:
| $ x_{\mathrm{best}, j}^{iter}=\frac{l b_j+u b_j}{2}+\frac{l b_j+u b_j}{2 k^{\prime}}-\frac{x_{\mathrm{best}, j}^{i t e r}}{k^{\prime}}, $ | (14) |
| $ x_{\text {best }, j}^{iter+1}=x_{\text {best }, j}^{iter}+x_{\text {best }, j}^{iter} \otimes \text { cauchy }(0, 1), $ | (15) |
其中, k′为缩放因子,
综上, CSCA-CBS的算法实现步骤如下:
算法1 CSCA-CBS算法
初始化: Logistic-Tent混沌序列初始化种群。
① 评估种群位置并排序, 并记录个体最优和全局最优。
② iter=1
③ while (iter<Max_iter)
④ for i=1∶N
⑤ for j=1∶D
⑥ 根据公式(3), (12), (13)计算r1, P(c4), sign(c4);
⑦ 产生[0, 2π], [0, 2], [0, 1]之间的随机数r2, r3, r4;
⑧ 根据公式(10)更新个体位置;
⑨ end for
⑩ 更新个体最优和全局最优;
⑪ 根据公式(14)产生种群的反向解;
⑫ 根据公式(15)对种群进行扰动, 确定全局最优解;
⑬ end for
⑭ iter=iter+1
⑮ end while
⑯ 输出全局最优解和最优适应度。
3 实验与结果分析 3.1 实验设置为了合理评估CSCA-CBS的优化性能, 选取15个常用的基准测试函数[30](表 1), 并设置种群规模N为50, 最大迭代次数Max_iter为1 000, 维度分别为30和100, 以确保实验的可靠性和公平性。其中, CSCA-CBS中的控制参数α=2, 疯狂因子xcraziness=0.000 1, 缩放因子k′=10 000。为了全面评估算法性能, 本文采用“平均值±标准差”的形式呈现结果, 并记录各函数收敛的平均迭代次数(AI)和优化成功率(SR), 以衡量算法的计算代价和可靠性, 保障数值结果的可靠性。
| 函数名称 Function name |
取值范围 Scope |
理论最优值 Optimum value |
精度阈值 Accuracy |
| f1: Sphere | [-100, 100] | 0 | 1e-6 |
| f2: Generalized rosenbrock | [-100, 100] | 0 | 1e+2 |
| f3: Ackley | [-32, 32] | 0 | 1e-6 |
| f4: Generalized griewank | [-600, 600] | 0 | 1e-6 |
| f5: Generalized rastrigin | [-5.12, 5.12] | 0 | 5e+1 |
| f6: Non-continuous rastrigin | [-500, 500] | 0 | 5e+1 |
| f7: Schwefel′s function 2.26 | [-500, 500] | 0 | 2e+3 |
| f8: Schwefel′s function 1.2 | [-100, 100] | 0 | 1e-6 |
| f9: Schwefel′s function 1.2.1 | [-100, 100] | 0 | 1e-6 |
| f10: High conditioned elliptic | [-100, 100] | 0 | 1e-6 |
| f11: Weierstrass | [-0.5, 0.5] | 0 | 1e-6 |
| f12: Schwefel′s function 2.22 | [-10, 10] | 0 | 1e-6 |
| f13: Schwefel′s function 2.21 | [-100, 100] | 0 | 1e-6 |
| f14: Generalized penalized 1 | [-50, 50] | 0 | 1e-6 |
| f15: Generalized penalized 2 | [-50, 50] | 0 | 1e-6 |
当求解最优值fmin(x)与理论最优值f*之间的距离|fmin(x)-f*|≤θ时, 即代表优化成功, 并记录此时的迭代次数。其中, θ表示精度阈值, 根据文献[31-32], 设置见表 1所示。整个数值仿真实验的工作硬件环境:操作系统为Windows 11, CPU为Intel (R) Core(TM) i5-1155G7, 主频为2.50 GHz, 内存为8 GB;编程软件为MATLAB 2021a。
3.2 不同改进策略的有效性分析为了分析不同改进策略对SCA优化性能的影响, 本节将原始SCA、基于Logistic-Tent序列的SCA(简称CSCA)、基于疯狂秃鹰搜索策略的SCA(简称CBSSCA)、结合逐维反向柯西变异策略的SCA(简称DRCSCA)同时用于求解表 1中15个基准函数。
由表 2可知, 由Logistic-Tent映射组合而成的CSCA在增加种群多样性的同时保证了种群的均匀分布, 因此在SCA的基础上使收敛效果明显提升1至3个数量级。引入疯狂算子对种群进行微小扰动后, 能使种群在充分搜索的过程中维持多样性。对于较难收敛的f2、f7、f14、f15, CBSSCA的性能相较于SCA提升了0至4个数量级, 而对于其余测试函数, CBSSCA在4个函数上达到了理论最优值。尽管Logistic-Tent映射和疯狂算子的加入使SCA在收敛速度和精度上均取得满意结果, 但SCA在迭代过程中仍会逐渐收敛到局部最优。为此, 在迭代后期提出了逐维反向柯西变异策略。从表 2可以看出, DRCSCA相较于SCA收敛性显著增强, 这表明逐维反向柯西变异策略的应用使算法性能得到了大幅提升。实验结果表明, 3种策略的引入均对算法性能产生积极影响, 且逐维反向柯西变异策略的效果最为显著。将3种策略融合后, CSCA-CBS在各个阶段都表现出更优异的性能。具体而言, 融合策略在算法的初始阶段、收敛阶段以及避免陷入局部最优方面均展现出明显的优势。
| 函数 Function |
SCA | CSCA | CBSSCA | DRCSCA | CSCA-CBS |
| f1 | 1.41E-04±3.92E-04 | 7.79E-06±1.37E-05 | 7.56E-186±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f2 | 1.24E+02±3.54E+02 | 6.57E+01±1.03E+02 | 2.66E+01±8.13E-01 | 2.87E+01±1.41E-01 | 2.88E+01±1.77E-01 |
| f3 | 1.29E+01±9.23E+00 | 1.27E+01±8.36E+00 | 1.40E+01±9.67E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f4 | 1.09E-01±2.03E-01 | 1.87E-01±1.74E-01 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f5 | 1.30E+01±3.12E+01 | 8.82E-01±1.49E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f6 | 7.32E+01±4.67E+01 | 6.10E+01±5.05E+01 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f7 | 8.26E+03±3.25E+02 | 8.37E+03±2.41E+02 | 5.80E+03±6.02E+02 | 9.72E+03±2.95E+02 | 9.28E+03±3.42E+02 |
| f8 | 9.65E+02±1.17E+03 | 1.29E+02±2.04E+02 | 1.17E-58±1.35E-58 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f9 | 2.16E+05±2.58E+05 | 3.06E+05±2.89E+05 | 3.52E+05±6.10E+05 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f10 | 1.03E-04±2.99E-04 | 7.10E-05±1.38E-04 | 1.09E-185±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f11 | 1.29E-05±2.61E-05 | 1.47E-05±2.97E-05 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f12 | 4.34E-07±5.97E-07 | 1.94E-08±3.74E-07 | 5.18E-96±8.53E-96 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f13 | 7.54E+00±5.80E+00 | 9.50E+00±1.01E+01 | 1.70E-30±4.12E-30 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f14 | 1.56E+03±3.62E+03 | 4.91E+03±1.19E+04 | 3.77E-01±5.60E-02 | 1.12E+00±3.66E-02 | 9.68E-01±1.30E-01 |
| f15 | 2.16E+00±1.88E-01 | 2.09E+00±2.34E-01 | 1.19E+00±3.49E-01 | 2.80E+00±3.27E-02 | 2.83E+00±1.03E-01 |
| Note: data in bold are the optimal results. | |||||
3.3 对比实验
选择ASCA[33]、IWCCSCA[34]、OBSCA[35]以及IM-CSA[36]等4种对比算法来展现本文所提出的CSCA-CBS的竞争力。本文将从计算代价和可靠性、解的质量分析以及收敛性能这3个方面进行详细比较。对比算法的各参数均按照对应文献进行设置, 所有测试函数结果均独立执行30维。
3.3.1 计算代价和可靠程度本文采用AI和SR这两个指标来评价各算法的计算代价和可靠性。30维独立运行的AI和SR结果见表 3。本文所提出的CSCA-CBS由于在初始化、全局探测以及后期开发阶段都对种群多样性进行了有效提升, 大大加快了算法的搜索速度。这使得CSCA-CBS在优化的12个函数中均实现了100%的成功率。另外, 由于将透镜成像反向学习策略引入到后期种群的大扰动阶段, CSCA-CBS极度地减小了计算代价, 平均仅迭代几次就可以达到所需精度。综合来看, 本文所提出的CSCA-CBS在计算代价和可靠程度方面表现最佳。
| 函数 Function |
SCA | CSCA | CBSSCA | DRCSCA | CSCA-CBS | |||||||||
| AI | SR | AI | SR | AI | SR | AI | SR | AI | SR | |||||
| f1 | N.A. | 0% | 76.43 | 100% | 51.81 | 100% | 51.81 | 100% | 1.00 | 100% | ||||
| f2 | 341.60 | 100% | 32.77 | 100% | 33.44 | 100% | 33.44 | 100% | 0.00 | 100% | ||||
| f3 | N.A. | 0% | 108.17 | 100% | 73.67 | 100% | 73.67 | 100% | 1.53 | 100% | ||||
| f4 | 968.97 | 6.67% | 74.17 | 100% | 62.00 | 100% | 62.00 | 100% | 1.00 | 100% | ||||
| f5 | 23.43 | 100% | 29.37 | 100% | 17.40 | 100% | 17.40 | 100% | 0.00 | 100% | ||||
| f6 | 617.53 | 73.33% | 48.57 | 100% | 37.60 | 100% | 37.60 | 100% | 0.20 | 100% | ||||
| f7 | 9.23 | 100% | 21.73 | 100% | N.A. | 0% | N.A. | 0% | N.A. | 0% | ||||
| f8 | N.A. | 0% | 79.23 | 100% | 295.00 | 100% | 295.00 | 100% | 0.97 | 100% | ||||
| f9 | N.A. | 0% | 111.70 | 100% | 197.00 | 100% | 197.00 | 100% | 1.10 | 100% | ||||
| f10 | 978.87 | 3.33% | 68.80 | 100% | 52.61 | 100% | 52.61 | 100% | 1.00 | 100% | ||||
| f11 | N.A. | 0% | 150.53 | 100% | 783.42 | 40% | 783.42 | 40% | 2.13 | 100% | ||||
| f12 | 984.30 | 3.33% | 102.27 | 100% | 69.20 | 100% | 69.20 | 100% | 1.73 | 100% | ||||
| f13 | N.A. | 0% | 118.63 | 100% | 103.01 | 100% | 103.01 | 100% | 1.73 | 100% | ||||
| f14 | N.A. | 0% | N.A. | 0% | N.A. | 0% | N.A. | 0% | N.A. | 0% | ||||
| f15 | N.A. | 0% | 976.70 | 3.33% | N.A. | 0% | N.A. | 0% | N.A. | 0% | ||||
| Note: data in bold are the optimal results.“N.A.” indicates a solution failure, i.e., the result still does not reach the threshold accuracy at the end of 1 000 iterations θ. | ||||||||||||||
3.3.2 解的质量分析
5种不同SCA变体求解15个基准函数在30维下的质量分析见表 4。本文通过Wilcoxon秩和检验进行统计, 显著性水平为0.05。由表 4可知, 与ASCA、IWCCSCA、OBSCA和IM-SCA相比, CSCA-CBS能够在11个函数上获得更优的结果, 并且这11个函数均获得理论最优值。对比ASCA, CSCA-CBS在除f2、f7、f14、f15以外均取得了更优结果。与IWCCSCA相比, CSCA-CBS分别在6个函数上获得最优结果以及在5个函数上取得相似结果, 但在f2上略逊一筹。与OBSCA相比, CSCA-CBS在6个函数上表现更优。而与IM-SCA相比, CSCA-CBS有4个较优和8个同等结果。综上, 本文所提的CSCA-CBS虽然在f2、f7、f14、f15这4个函数上与其他SCA变体一样陷入局部最优, 但在剩下的11个函数均取得了理论最优, 说明CSCA-CBS能够在大多数函数上充分对搜索空间进行探索, 并具备较强的全局优化能力。为了观察和分析维度变化对算法性能的影响, 表 5列出了在其他参数不变、问题维度为100维的条件下5种SCA变体的求解精度, 每个算法分别独立运行30次并取平均值。由表 5可知, CSCA-CBS的性能依然是最好的, 对于f1、f3-f6、f8-f13, CSCA-CBS在30次实验中均能找到理论最优解。
| 函数 Function |
ASCA | IWCCSCA | OBSCA | IM-SCA | CSCA-CBS |
| f1 | 1.28E-01±2.87E-01 | 7.19E-128±3.94E-127 | 1.78E-247±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f2 | 9.15E+00±1.34E+01 | 2.83E+01±4.82E-01 | 2.83E+01±4.84E-01 | 2.78E+01±7.01E-01 | 2.88E+01±1.77E-01 |
| f3 | 3.10E-02±4.59E-02 | 0.00E+00±0.00E+00 | 3.55E-15±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f4 | 1.31E-01±2.40E-01 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f5 | 5.65E-02±1.29E-01 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f6 | 3.83E+01±4.87E+01 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f7 | 1.36E-02±1.71E-02 | 5.81E+02±6.66E+01 | 8.42E+03±2.00E+02 | 1.07E+04±2.06E+02 | 9.28E+03±3.42E+02 |
| f8 | 4.29E+01±7.77E+01 | 4.20E-127±2.17E-126 | 4.60E-53±1.03E-52 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f9 | 1.58E+04±3.84E+04 | 6.29E-112±3.44E-111 | 2.24E-84±3.10E-84 | 6.83E-292±0.00E+00 | 0.00E+00±0.00E+00 |
| f10 | 5.12E-02±2.00E-01 | 2.80E-133±1.53E-132 | 1.65E-247±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f11 | 9.11E-03±2.60E-02 | 0.00E+00±0.00E+00 | 2.11E+01±2.63E+01 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f12 | 1.04E-04±1.57E-04 | 1.29E-68±6.37E-68 | 4.04E-149±8.89E-149 | 3.42E-191±0.00E+00 | 0.00E+00±0.00E+00 |
| f13 | 1.83E-02±1.51E-02 | 1.95E-64±1.06E-63 | 1.35E-72±2.98E-72 | 2.94E-168±0.00E+00 | 0.00E+00±0.00E+00 |
| f14 | 7.80E-02±2.63E-02 | 3.01E-01±2.66E-01 | 3.62E+01±5.09E+00 | 7.40E-01±4.30E-02 | 9.68E-01±1.30E-01 |
| f15 | 5.11E-03±1.58E-02 | 1.12E+00±1.10E+00 | 1.72E+00±1.91E-01 | 9.48E-01±1.06E-01 | 2.83E+00±1.03E-01 |
| +/≈/- | 4/0/11 | 1/5/9 | 2/3/10 | 3/8/4 | -/-/- |
| Note: data in bold are the optimal results.-, +, and ≈ indicate that the compared algorithms are significantly inferior, superior, and approximately equal to CSCA-CBS, respectively. | |||||
| 函数 Function |
ASCA | IWCCSCA | OBSCA | IM-SCA | CSCA-CBS |
| f1 | 9.02E-02±1.59E-01 | 2.41E-127±1.15E-126 | 5.94E-160±1.25E-159 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f2 | 7.26E+00±1.14E+01 | 9.82E+01±2.59E-01 | 1.39E+02±9.03E+01 | 9.87E+01±2.42E-01 | 9.89E+01±4.81E-02 |
| f3 | 3.80E-02±5.52E-02 | 0.00E+00±0.00E+00 | 3.55E-15±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f4 | 7.53E-02±1.48E-01 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f5 | 2.93E-02±4.34E-02 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f6 | 2.65E+02±23.37E+02 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f7 | 3.56E-02±5.24E-02 | 2.30E+03±1.51E+02 | 3.37E+04±5.63E+02 | 3.92E+04±3.87E+02 | 3.58E+04±7.61E+02 |
| f8 | 6.46E+03±5.07E+03 | 5.70E-119±3.12E-118 | 4.90E+03±6.74E+03 | 9.71E-258±0.00E+00 | 0.00E+00±0.00E+00 |
| f9 | 2.12E+12±1.38E+12 | 9.24E-41±4.94E-40 | 9.09E-02±2.00E-01 | 6.23E-167±0.00E+00 | 0.00E+00±0.00E+00 |
| f10 | 8.20E-02±1.41E-01 | 3.33E-115±1.82E-114 | 1.71E-161±3.79E-161 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f11 | 2.30E+00±1.81E+00 | 0.00E+00±0.00E+00 | 1.40E+02±7.85E+01 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f12 | 1.89E-01±1.74E-01 | 8.08E-63±4.43E-62 | 5.99E-94±1.23E-93 | 2.10E-172±0.00E+00 | 0.00E+00±0.00E+00 |
| f13 | 2.17E-02±1.93E-02 | 4.64E-62±2.52E-61 | 3.34E+01±1.66E+01 | 1.84E-116±9.98E-116 | 0.00E+00±0.00E+00 |
| f14 | 4.00E-02±1.03E-01 | 1.70E-01±2.52E-01 | 2.13E+01±4.52E+00 | 1.07E+00±6.77E-02 | 1.14E+00±6.30E-02 |
| f15 | 2.55E-03±3.17E-03 | 3.27E+00±3.77E+00 | 7.33E+01±6.61E+01 | 3.97E+00±1.78E-01 | 9.88E+00±3.01E-02 |
| +/≈/- | 4/0/11 | 0/5/10 | 0/3/12 | 0/6/9 | -/-/- |
| Note: data in bold are the optimal results.-, +, and ≈ indicate that the compared algorithms are significantly inferior, superior, and approximately equal to CSCA-CBS, respectively. | |||||
3.3.3 收敛性能
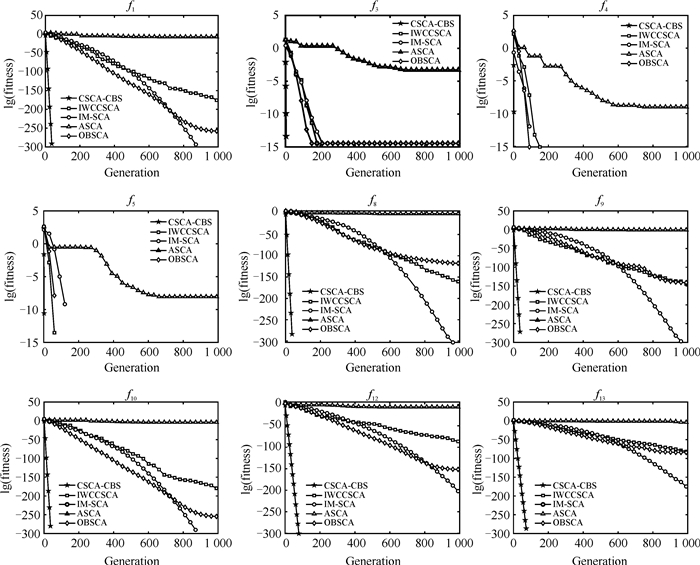
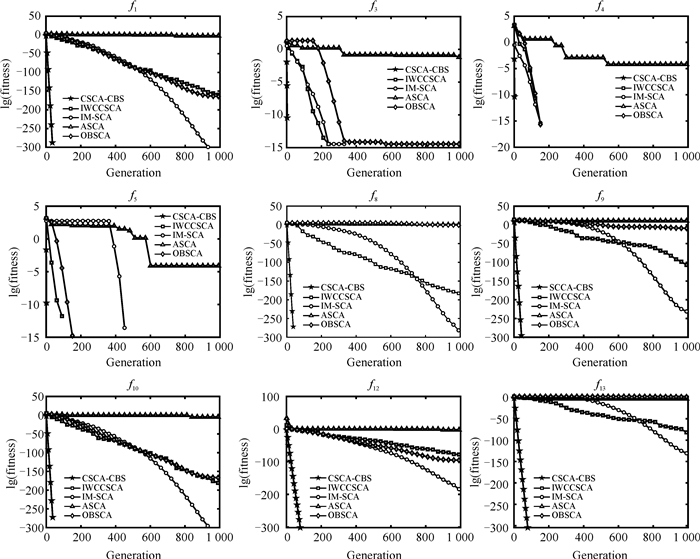
图 2和图 3分别展示了CSCA-CBS以及其他几种改进的SCA变体基准算法在维度为30和100时对9个基准函数的收敛曲线, 以直观地展示算法的收敛速度和全局搜索能力。从图 2、3可以看出, 无论在低维(维度30)还是高维(维度100)的情况下, 当迭代次数不到100次时, 本文所提出的CSCA-CBS可以找到9个函数的全局最优值, 而对比算法则需要迭代到接近1 000次才能接近或达到最优值, 有的算法甚至会在迭代过程中陷入局部最优。因此, 无论函数特征如何, CSCA-CBS均展现出强大的全局最优搜索能力。
|
| 图 2 CSCA-CBS、ASCA、IWCCSCA、OBSCA、IM-SCA的收敛曲线(30维) Fig. 2 Convergence curves of CSCA-CBS, ASCA, IWCCSCA, OBSCA, and IM-SCA (30 D) |
|
| 图 3 CSCA-CBS、ASCA、IWCCSCA、OBSCA、IM-SCA的收敛曲线(100维) Fig. 3 Convergence curves of CSCA-CBS, ASCA, IWCCSCA, OBSCA, and IM-SCA (100 D) |
综上, 相对于ASCA、IWCCSCA、OBSCA和IM-SCA, CSCA-CBS在计算代价和可靠程度、解的质量分析、收敛性能方面都具有显著优势。
3.4 与非SCA比较为了进一步测试CSCA-CBS在其他非SCA中的显著优势, 选用了近3年内开发的4种优秀算法进行比较, 包括IAGA[30]、SOGWO[37]、ICS-FG[38]、EFPA-G[39]。表 6列出IAGA、SOGWO、ICS-FG、EFPA-G和CSCA-CBS在30维下独立运行30次后获得的平均值和标准差, 其中算法参数设置来源于其对应文献。
| 函数 Function |
IAGA | SOGWO | ICS-FG | EFPA-G | CSCA-CBS |
| f1 | 1.54E-32±6.44E-32 | 4.92E-85±1.79E-84 | 2.02E-88±1.10E-87 | 2.82E-269±0.00E+00 | 0.00E+00±0.00E+00 |
| f2 | 2.44E+01±9.75E+00 | 2.61E+01±6.00E-01 | 2.83E+01±3.80E-01 | 2.87E+01±6.90E-02 | 2.88E+01±1.77E-01 |
| f3 | 2.96E-15±1.35E-15 | 9.59E-15±2.66E-15 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f4 | 0.00E+00±0.00E+00 | 1.01E-03±4.07E-03 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f5 | 0.00E+00±0.00E+00 | 1.78E-01±9.74E-01 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f6 | 0.00E+00±0.00E+00 | 2.50E+00±4.57E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f7 | 8.94E-02±4.22E-02 | 6.10E+03±7.61E+02 | 4.47E+03±1.37E+02 | 6.91E+03±6.56E+02 | 9.28E+03±3.42E+02 |
| f8 | 3.51E-35±8.14E-35 | 3.21E-27±1.30E-26 | 8.51E-08±4.66E-07 | 1.85E-266±0.00E+00 | 0.00E+00±0.00E+00 |
| f9 | 4.51E-20±9.39E-20 | 3.98E+02±2.12E+03 | 2.34E-61±1.06E-60 | 8.17E-225±0.00E+00 | 0.00E+00±0.00E+00 |
| f10 | 1.08E-32±2.19E-32 | 6.82E-85±3.21E-84 | 7.26E-100±3.98E-99 | 3.67E-267±0.00E+00 | 0.00E+00±0.00E+00 |
| f11 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 | 0.00E+00±0.00E+00 |
| f12 | 2.14E-22±3.57E-22 | 2.93E-49±2.65E-49 | 2.32E-34±1.25E-33 | 6.22E-135±2.86E-134 | 0.00E+00±0.00E+00 |
| f13 | 4.83E-13±5.86E-13 | 2.36E-21±6.80E-21 | 8.87E-35±4.86E-34 | 3.98E-135±8.68E-135 | 0.00E+00±0.00E+00 |
| f14 | 4.67E-01±6.36E-01 | 1.39E+00±4.50E+00 | 3.62E-01±1.29E-01 | 1.22E-01±5.20E-02 | 9.68E-01±1.30E-01 |
| f15 | 5.74E-01±8.26E-01 | 1.72E-01±1.18E-01 | 2.13E+00±8.53E-02 | 2.21E-02±1.76E-02 | 2.83E+00±1.03E-01 |
| +/≈/- | 4/4/7 | 3/1/11 | 3/5/7 | 4/5/6 | -/-/- |
| Note: data in bold are the optimal results.-, +, and ≈ indicate that the compared algorithms are significantly inferior, superior, and approximately equal to CSCA-CBS, respectively. | |||||
由表 6可知, 相比于IAGA, CSCA-CBS对函数f2、f7、f14、f15的优化结果较差, 而对于f4、f5、f6、f11这4个函数均能够搜索到全局最优解;CSCA-CBS对函数f2、f7、f15的优化结果同样差于SOGWO、ICS-FG和EFPA-G, 但所有算法对f11有着一样的优化效果;对于ICS-FG和EFPA-G来说, 对函数f3、f4、f5、f6、f11的优化效果与CSCA-CBS相近。综上, CSCA-CBS在数值优化结果、稳定性等方面都比IAGA、SOGWO、ICS-FG、EFPA-G优异。
3.5 非参数检验为了进一步证明本文所提出的CSCA-CBS的显著性能, 本文采用两种非参数统计检验方法(包括Friedman检验和Kruskal-Wallis检验)来对上述所有比较算法进行分析和排名。
表 7列出了对所有基准测试函数在30维下的求解性能排名统计情况。每个算法及其排名均按升序列出(得分越低越好)。如表 7所示, 10种算法在两次非参数统计检验中的排名几乎一致, 本文所提算法CSCA-CBS在优化问题中的综合实力为第一名, 其中OBSCA和ICS-FG的排名略有不同。Friedman检验和Kruskal-Wallis检验方法表明, 与其他9种先进算法相比, CSCA-CBS明显更好, 相对原始SCA来说有着显著的性能改进。
| 排名 Rank |
Friedman | Kruskal-Wallis | |||
| 算法 Algorithm |
得分 Score |
算法 Algorithm |
得分 Score |
||
| 1 | CSCA-CBS | 2.60 | CSCA-CBS | 54.33 | |
| 2 | IM-SCA | 2.73 | IM-SCA | 62.17 | |
| 3 | EFPA-G | 2.80 | EFPA-G | 66.21 | |
| 4 | IWCCSA | 3.27 | IWCCSA | 77.02 | |
| 5 | ICS-FG | 4.33 | OBSCA | 84.57 | |
| 6 | OBSCA | 4.47 | ICS-FG | 85.02 | |
| 7 | IAGA | 4.53 | IAGA | 90.75 | |
| 8 | SOGWO | 6.40 | SOGWO | 109.99 | |
| 9 | ASCA | 8.20 | ASCA | 130.54 | |
| 10 | SCA | 9.27 | SCA | 150.16 | |
4 土壤水分特征曲线参数反演问题
为了验证本文所提出的CSCA-CBS在实际应用上的实用性和有效性, 将其应用于土壤水分特征曲线的参数反演问题上。
4.1 问题描述土壤水分特征曲线是获得土壤学传导率的常用手段, 也是定量分析土壤水分含量并用于预测的重要理论依据。Van Genuchten (VG)方程是目前来说使用最为广泛的模型, 具体表达式如下:
| $ \theta(h)=\frac{\theta_s-\theta_r}{\left[1+|\alpha h|^N\right]^M}+\theta_r, $ | (16) |
式中, θ(h)是不同土壤吸水力h下的土壤含水率;θs是土壤饱和含水率;θr是土壤残余含水率;α、N、M为土壤水分特征曲线的形状参数, M=1-1/N, N>1。由式(16)可知, [θs, θr, α, N]是需要根据实测数据待反演的4个参数。
本文使用绝对值误差来构成目标函数, 反演的最优参数如公式(17)所示:
| $ \left[\theta_s, \theta_r, \alpha, N\right]=\operatorname{argmin}\left\{\sum\limits_{i=1}^m\left|\theta(h)-\theta_i\right|\right\}, $ | (17) |
其中, θi为实测土壤含水率, m为实测数据组数。
4.2 数值实验在VG方程参数反演的数值实验中, 土壤数据来源于对西北某干旱地区的实测采集[40]。本节主要分为两个部分:①比较不同方法对粉壤土的求解结果, 主要将SCA、CSCA-CBS与非线性单纯形法(SM)、阻尼最小二乘法(DLSM)、遗传算法(GA)、混合遗传算法(HGA)、随机粒子群算法(SPSO)、混合粒子群算法(HPSO)的求解结果进行比较;②比较不同改进方法对3种类型土壤VG方程的求解精度和优化性能, 主要包括HPSO[41]、改进PSO(IPSO)[42]以及SCA, 并将反演结果与实测值进行比较。VG方程参数的取值范围是θs∈[0.2, 0.7], θr∈[0.0, 0.2], α∈[0, 1], n∈[1, 10]。种群规模N=200, 最大迭代次数为1 000。整个数值实验均独立运行40次。
表 8列出了使用SM、DLSM、GA、HGA、SPSO、HPSO、SCA和CSCA-CBS对粉壤土VG方程进行参数反演的结果, 其中SM、DLSM、GA、HGA、SPSO、HPSO的求解数据来源于文献[41]。由表 8可知, GA和HPSO的反演结果较为相似, 其函数值误差仅相差0.000 1, 于是可将粉壤土VG方程的参数θr和θs分别锁定为0.057和0.363;其次, 将CSCA-CBS与GA进行比较, 可进一步将参数α锁定为0.014, 并且CSCA-CBS的最优函数误差值达到最小, 证明了其在粉壤土中的应用效果。
| 算法 Algorithm |
θr | θs | α | N | 函数值 Function value |
| SM | 0.053 | 0.363 | 0.013 | 4.241 | 0.108 2 |
| DLSM | 0.053 | 0.363 | 0.014 | 4.197 | 0.147 3 |
| GA | 0.057 | 0.363 | 0.014 | 2.945 | 0.063 8 |
| HGA | 0.066 | 0.358 | 0.014 | 4.073 | 0.077 9 |
| SPSO | 0.066 | 0.359 | 0.013 | 4.044 | 0.077 4 |
| HPSO | 0.057 | 0.363 | 0.013 | 3.167 | 0.063 9 |
| SCA | 0.061 | 0.364 | 0.012 | 3.267 | 0.065 1 |
| CSCA-CBS | 0.057 | 0.363 | 0.014 | 2.949 | 0.061 7 |
| Note: data in bold are the optimal results. | |||||
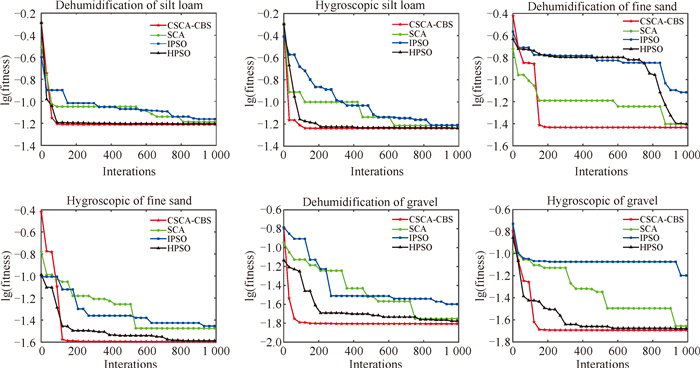
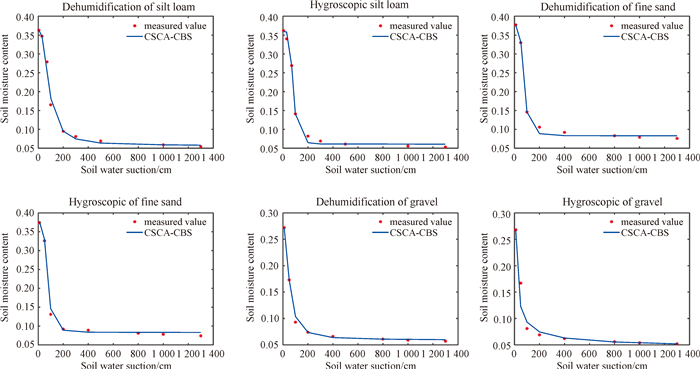
表 9给出了CSCA-CBS与SCA、IPSO、HPSO在3类土壤(粉壤土、细砂和砾石)下的参数反演结果, 其中每种土壤具有脱湿和细湿两种情况。从计算的最优函数值来看, CSCA-CBS无论在哪种土壤下都能获得最优的函数值。由图 4可以看出, CSCA-CBS在迭代搜索过程中均表现出比其他方法更好的优化性能, 特别是对于细砂和砾石这两种土壤。另外, CSCA-CBS也能够在不同土壤环境下计算出与实际测量值十分吻合的反演参数, 如图 5所示。综上所述, 本文提出的CSCA-CBS可用于求解VG方程的参数反演问题, 并能提供一种比较可靠的解决方案。
| 土壤类型 Soil type |
算法 Algorithm |
θr | θs | α | n | 函数值 Function value |
| Dehumidification of silty loam | HPSO | 0.057 | 0.362 | 0.014 | 2.983 | 0.062 5 |
| IPSO | 0.064 | 0.360 | 0.013 | 3.323 | 0.069 1 | |
| SCA | 0.058 | 0.365 | 0.014 | 3.176 | 0.065 1 | |
| CSCA-CBS | 0.057 | 0.363 | 0.014 | 2.949 | 0.061 7 | |
| Hygroscopic of silt loam | HPSO | 0.061 | 0.347 | 0.013 | 5.779 | 0.058 2 |
| IPSO | 0.059 | 0.354 | 0.013 | 3.625 | 0.061 6 | |
| SCA | 0.000 | 0.368 | 0.015 | 2.111 | 0.061 2 | |
| CSCA-CBS | 0.061 | 0.361 | 0.013 | 5.501 | 0.057 8 | |
| Dehumidification of fine sand | HPSO | 0.083 | 0.377 | 0.015 | 4.442 | 0.039 4 |
| IPSO | 0.050 | 0.700 | 0.330 | 1.542 | 0.076 7 | |
| SCA | 0.000 | 0.700 | 0.550 | 1.349 | 0.039 5 | |
| CSCA-CBS | 0.083 | 0.377 | 0.01 | 4.622 | 0.036 9 | |
| Hygroscopic of fine sand | HPSO | 0.081 | 0.374 | 0.015 | 5.012 | 0.025 9 |
| IPSO | 0.059 | 0.700 | 0.271 | 1.648 | 0.035 2 | |
| SCA | 0.083 | 0.371 | 0.015 | 5.170 | 0.033 6 | |
| CSCA-CBS | 0.081 | 0.374 | 0.015 | 5.013 | 0.025 4 | |
| Dehumidification of gravel | HPSO | 0.060 | 0.275 | 0.024 | 2.801 | 0.016 7 |
| IPSO | 0.048 | 0.700 | 0.417 | 1.707 | 0.025 2 | |
| SCA | 0.058 | 0.273 | 0.023 | 3.033 | 0.017 7 | |
| CSCA-CBS | 0.061 | 0.273 | 0.023 | 3.223 | 0.015 6 | |
| Hygroscopic of gravel | HPSO | 0.045 | 0.589 | 0.322 | 1.718 | 0.020 9 |
| IPSO | 0.043 | 0.700 | 0.465 | 1.674 | 0.063 4 | |
| SCA | 0.056 | 0.268 | 0.022 | 3.593 | 0.022 1 | |
| CSCA-CBS | 0.056 | 0.269 | 0.022 | 3.630 | 0.020 3 | |
| Note: data in bold are the optimal results. | ||||||
|
| 图 4 VG方程参数反演平均迭代曲线 Fig. 4 Average iteration curves for parametric inversion of the VG equations |
|
| 图 5 CSCA-CBS对不同土壤水分特征曲线的反演结果 Fig. 5 Inversion results of CSCA-CBS for different soil moisture characteristic curves |
5 结论
本文提出了一种融合疯狂秃鹰搜索算法的混沌正余弦算法CSCA-CBS, 主要从3个方面进行改进:①引入一种混合的混沌映射策略, 以提升初始种群的多样性;②采用疯狂秃鹰搜索策略, 以增强原始SCA的全局探索能力;③提出逐维反向变异策略, 以帮助种群跳出局部最优。为检验CSCA-CBS的可靠性,本文在不同维度和不同测试函数下进行了广泛的对比实验。结果表明,与先进的SCA变体以及非SCA相比, CSCA-CBS在收敛速度和精度上均优于对比算法。随后, 利用CSCA-CBS求解土壤水分特征曲线参数的结果表明, CSCA-CBS具有更快的计算速度和更高的求解精度, 极大地提高了参数优化的普适性, 这为解决VG方程问题提供了有效方法。
| [1] |
郑立辉, 郭亚军, 潘德惠. 一种基于梯度搜索的全局优化新算法[J]. 控制理论与应用, 1997, 14(3): 343-348. |
| [2] |
WU M, OU X F, LU Y L, et al. Heterogeneous Cuckoo search-based unsupervised band selection for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 62: 1-16. |
| [3] |
MEHEDI I M, AHMADIPOUR M, SALAM Z, et al. Optimal feature selection using modified cuckoo search for classification of power quality disturbances[J]. Applied Soft Computing, 2021, 113: 107897. DOI:10.1016/j.asoc.2021.107897 |
| [4] |
XIONG Y B, WU J, WANG Q, et al. SAPNN: self-adaptive probabilistic neural network for medical diagnosis[J]. International Journal of Computational Science and Engineering, 2024, 27(1): 68-77. DOI:10.1504/IJCSE.2024.136252 |
| [5] |
王伟, 龙文. 动态透镜成像学习人工兔优化算法及应用[J]. 广西科学, 2023, 30(4): 735-744. DOI:10.13656/j.cnki.gxkx.20230928.013 |
| [6] |
MIRJALILI S. SCA: a sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120-133. DOI:10.1016/j.knosys.2015.12.022 |
| [7] |
LIU J S, ZHAO F Y, LI Y, et al. A new global sine cosine algorithm for solving economic emission dispatch problem[J]. Information Sciences, 2023, 648: 119569. DOI:10.1016/j.ins.2023.119569 |
| [8] |
AKAY R, YILDIRIM M Y. Multi-strategy and self-adaptive differential sine-cosine algorithm for multi-robot path planning[J]. Expert Systems with Applications, 2023, 232: 120849. DOI:10.1016/j.eswa.2023.120849 |
| [9] |
文武, 万玉辉, 文志云. 基于正余弦算法的文本特征选择[J]. 计算机工程与科学, 2022, 44(8): 1467-1473. |
| [10] |
蒋杰伟, 金库, 刘尚辉, 等. 基于正余弦扰动的海洋捕食者算法优化RFA设计[J]. 光电子·激光, 2023, 34(7): 673-681. |
| [11] |
RIZK-ALLAH R M, HASSANIEN A E. A comprehensive survey on the sine-cosine optimization algorithm[J]. Artificial Intelligence Review, 2023, 56(6): 4801-4858. DOI:10.1007/s10462-022-10277-3 |
| [12] |
王庆, 李玉琛, 蒙飞, 等. 混沌正余弦算法在含风能电力系统经济排放调度中的应用[J]. 电力系统保护与控制, 2022, 50(24): 172-177. |
| [13] |
JIAO S B, WANG C, GAO R, et al. A novel hybrid Harris hawk sine cosine optimization algorithm for reactive power optimization problem[J]. Journal of Experimental & Theoretical Artificial Intelligence, 2024, 36(6): 901-937. |
| [14] |
FENG Z K, DUAN J F, NIU W J, et al. Enhanced sine cosine algorithm using opposition learning, adaptive evolution and neighborhood search strategies for multivariable parameter optimization problems[J]. Applied Soft Computing, 2022, 119: 108562. |
| [15] |
王华秋, 熊维双. 采用聚类的变异正余弦优化算法研究[J]. 重庆理工大学学报(自然科学), 2022, 36(11): 292-302. |
| [16] |
CHEN H, HEIDARI A A, ZHAO X H, et al. Advanced orthogonal learning-driven multi-swarm sine cosine optimization: framework and case studies[J]. Expert Systems with Applications, 2020, 144: 113113. |
| [17] |
SINDHU R, NGADIRAN R, YACOB Y M, et al. Retraction note: sine-cosine algorithm for feature selection with elitism strategy and new updating mechanism[J]. Neural Computing and Applications, 2024, 36(18): 11019. |
| [18] |
RAUT U, MISHRA S. An improved sine-cosine algorithm for simultaneous network reconfiguration and DG allocation in power distribution systems[J]. Applied Soft Computing, 2020, 92: 106293. |
| [19] |
LIU J S, ZHAO F Y, LI Y, et al. A new global sine cosine algorithm for solving economic emission dispatch problem[J]. Information Sciences, 2023, 648: 119569. |
| [20] |
ISSA M, HASSANIEN A E, OLIVA D, et al. ASCA-PSO: adaptive sine cosine optimization algorithm integrated with particle swarm for pairwise local sequence alignment[J]. Expert Systems with Applications, 2018, 99: 56-70. |
| [21] |
GUPTA S, SU R, SINGH S. Diversified sine-cosine algorithm based on differential evolution for multidimensional knapsack problem[J]. Applied Soft Computing, 2022, 130: 109682. |
| [22] |
ANSARI S A, ZAFAR A. A fusion of dolphin swarm optimization and improved sine cosine algorithm for automatic detection and classification of objects from surveillance videos[J]. Measurement, 2022, 192: 110921. |
| [23] |
PHATAK S C, RAO S S. Logistic map: a possible random-number generator[J]. Physical Review E, 1995, 51(4): 3670-3678. |
| [24] |
李大海, 刘庆腾, 王振东. 融合Tent混沌和维度学习的阴阳对算法[J]. 计算机工程与设计, 2023, 44(8): 2320-2328. |
| [25] |
HERBADJI D, HERBADJI A, HADDAD I, et al. An enhanced logistic chaotic map based tweakable speech encryption algorithm[J]. Integration, 2024, 97: 102192. |
| [26] |
ZHANG Q Z, LIU H S, GUO J, et al. Improved GWOMCSVM algorithm based on nonlinear convergence factor and tent chaotic mapping and its application in transformer condition assessment[J]. Electric Power Systems Research, 2023, 224: 109754. |
| [27] |
高毅. 基于Logistic混沌算法的伪随机序列IP设计[D]. 哈尔滨: 黑龙江大学, 2021.
|
| [28] |
ALSATTAR H A, ZAIDAN A A, ZAIDAN B B. Novel meta-heuristic bald eagle search optimisation algorithm[J]. Artificial Intelligence Review, 2020, 53(3): 2237-2264. |
| [29] |
KALASHNIKOV V, KREINOVICH V, FLORESMUÑIZ J G, et al. Structure of filled functions: why Gaussian and Cauchy templates are most efficient[J]. International Journal of Combinatorial Optimization Problems and Informatics, 2016, 7(3): 87-93. |
| [30] |
OUYANG A J, LU Y S, LIU Y M, et al. An improved adaptive genetic algorithm based on DV-Hop for locating nodes in wireless sensor networks[J]. Neurocomputing, 2021, 458: 500-510. |
| [31] |
ZHAN Z H, ZHANG J, LI Y, et al. Orthogonal learning particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(6): 832-847. |
| [32] |
ZENG N Y, WANG Z D, LIU W B, et al. A dynamic neighborhood-based switching particle swarm optimization algorithm[J]. IEEE transactions on cybernetics, 2020, 52(9): 9290-9301. |
| [33] |
JI Y T, TU J Z, ZHOU H F, et al. An adaptive chaotic sine cosine algorithm for constrained and unconstrained optimization[J]. Complexity, 2020, 2020: 6084917. |
| [34] |
陈亮, 汤显峰. 改进正余弦算法优化特征选择及数据分类[J]. 计算机应用, 2022, 42(6): 1852-1861. |
| [35] |
ABD ELAZIZ M, OLIVA D, XIONG S. An improved opposition-based sine cosine algorithm for global optimization[J]. Expert Systems with Applications, 2017, 90: 484-500. |
| [36] |
刘丽娟, 刘定一, 刘婷婷. 改进的正余弦优化算法在WSN覆盖中的应用[J]. 数学的实践与认识, 2021, 51(11): 129-137. |
| [37] |
DHARGUPTA S, GHOSH M, MIRJALILI S, et al. Selective opposition based grey wolf optimization[J]. Expert Systems with Applications, 2020, 151: 113389. |
| [38] |
OU X F, WU M, PU Y Y, et al. Cuckoo search algorithm with fuzzy logic and Gauss-Cauchy for minimizing localization error of WSN[J]. Applied Soft Computing, 2022, 125: 109211. |
| [39] |
ZHENG J, YUAN T, XIE W W, et al. An enhanced flower pollination algorithm with Gaussian perturbation for node location of a WSN[J]. Sensors, 2023, 23(14): 6463. |
| [40] |
王金生, 杨志峰, 陈家军, 等. 包气带土壤水分滞留特征研究[J]. 水利学报, 2000, 31(2): 1-6. |
| [41] |
刘利斌, 欧阳艾嘉, 乐光学, 等. 基于混合粒子群的土壤水分特征曲线参数优化[J]. 计算机工程与应用, 2011, 47(35): 218-221. |
| [42] |
孙晓敏, 孙秋红. 基于改进的基本粒子群算法的Van Genuchten方程参数优化[J]. 水利与建筑工程学报, 2017, 15(5): 88-93. |



