2. 中国人民公安大学国家安全学院, 北京 100038;
3. 南宁职业技术学院人工智能学院, 广西南宁 530008
2. School of National Security, People's Public Security University of China, Beijing, 100038, China;
3. School of Artificial Intelligence, Nanning College for Vocational Technology, Nanning, Guangxi, 530008, China
图是一种常用的数据形式,用于表征实体间的关系,如引文网络中论文之间的互引信息、社交网络账号之间的关注信息等。节点分类[1]是利用图中已知的拓扑结构、节点属性以及节点标签等信息对无标签节点进行类别预测。因此,节点分类的关键在于如何提取原始图中蕴含的特征信息。图神经网络(Graph Neural Networks, GNN)[2]是一类高效的图特征学习方法,它通过传递和聚合节点间信息来生成保留拓扑结构和属性信息的低维节点表示,并将其用于节点分类等下游图分析任务。
近年来,已有许多研究对GNN进行改进,这些改进一般通过引入高效的信息传递和转换方式以增强GNN的表征能力。图卷积网络(Graph Convolutional Network, GCN)[3]将经典的卷积神经网络从欧式数据(图像、音频)推广到非欧式数据(图),实现了对拓扑结构和节点属性信息的编码,其在计算过程中仅使用节点的一阶邻域进行聚合,这提高了模型层间信息的传播效率。简化图卷积(Simplified Graph Convolution, SGC)[4]改进了GCN的编码策略,通过直接使用线性网络编码原始图信息以减少模型参数,降低模型复杂度;图注意力网络(Graph Attention Network, GAT)[5]在GCN的基础上引入注意力机制,为一阶邻域中各节点分配不同的权值,使信息聚合过程能够更加关注影响力较大的高权值邻居节点;GATv2[6]在GAT的基础上引入动态注意力机制,修改了GAT中权值计算过程,构建近似注意函数,从而提升了GAT的表征能力;结构感知路径聚合图神经网络(PathNet)[7]使用最大熵路径采集器采样节点上下文路径,然后引入结构感知循环单元学习上下文路径中蕴含的语义信息。由于浅层GNN架构限制了模型学习高阶邻域信息的能力,而深层GNN架构容易出现过平滑[8],为解决以上问题,Zhang等[9]提出的浅层双仿射图卷积网络(Shallow Biaffine Graph Convolutional Networks, BAGCN)不仅能够学习节点对远距离邻居的直接依赖性,还能通过一阶消息传递捕获多跳邻居的特征信息。
与上述通过复杂的节点信息传递和聚合方式提升模型性能的研究思路不同,本文提出了基于多层感知机(Multi-Layer Perceptron, MLP)[10]的A&T-MLP。A&T-MLP无需信息传递和聚合,而是通过属性和拓扑信息引导的对比损失以保留原始图相关特征。具体来说,A&T-MLP首先使用属性矩阵和邻接矩阵计算节点间的相似度信息;然后使用基于相似度信息引导的对比损失,优化MLP隐藏层生成的特征表示;最后引入交叉熵损失对A&T-MLP进行端到端训练。
1 相关工作 1.1 MLPMLP是一种基于前馈神经网络的深度学习模型,通常由输入层、隐藏层和输出层构成,相邻两层之间所有输入神经元都和输出神经元相连,因此也称为全连接神经网络。其中,输入层用于接收原始数据,隐藏层利用权重系数和激活函数对数据进行特征提取和非线性变换,输出层利用隐藏层生成的特征向量得到预测结果。MLP具有较强的表征能力,可通过特定的损失函数和反向传播算法对其进行训练优化。MLP能够自动地提取数据中蕴含的潜在信息,因此可用于分类、回归等机器学习任务。
在计算机视觉和自然语言处理领域,MLP被广泛应用于语音识别、图像识别、语义分割等众多任务。Hou等[11]提出了基于MLP的高效视觉识别架构,使用线性投影分别对高度和宽度特征表示进行编码,捕获长距离依赖关系,进而提升视觉识别网络的性能。Gong等[12]提出了基于Cycle-MLP的DriftNet模型,该模型通过神经元渐进激活以促进空间和光谱信息的融合,进而提升了高光谱图像像素分类的实验表现。Sun等[13]提出了多模态情绪分析模型CubeMLP,CubeMLP将所有模态特征作为输入,并将输入分配到3个不同的MLP单元提取特征,最后对混合多模态特征进行展平以实现情绪分析任务。在图分析领域,Hu等[14]提出了Graph-MLP,Graph-MLP通过拓扑结构中的邻接关系构建保留拓扑信息的对比损失,使仅使用节点属性作为输入的MLP能够匹配GCN在节点分类任务中的实验性能。
上述研究为MLP在其他领域的应用提供了理论基础,其性能也能够匹配多数复杂模型的实验表现。因此,本文在已有研究的基础上,提出了一种基于属性和拓扑信息增强MLP模型A&T-MLP,并应用于节点分类任务。
1.2 对比学习对比学习是从大量未标记的数据中提取可转移的特征,并将其扩展为特定的自监督信息[15],使模型在训练过程中能够对相似样本和不相似样本进行区分,因此对比学习的核心思想就是增大特征空间中同类数据表示的相似性和不同类数据表示的差异性。分类任务中常见的对比损失函数的表达式为
| $ \begin{array}{l} \quad\quad \operatorname{loss}\left(x_i\right)= \\ -\log \frac{\exp \left(s_{i, i}\right)}{\sum\nolimits_{k=1}^N \mathbf{1}_{[k \neq i]} \exp \left(s_{i, k}\right)+\exp \left(s_{i, i}\right)}, \end{array} $ | (1) |
式中,si,i表示正样本,si,k表示负样本。通过对比损失调整,使第i个数据与si,i之间的相似度尽可能大,与si,k之间的相似度尽可能小,从而提升模型表征原始数据信息的能力。
近年来,基于对比学习增强的图深度学习模型已成为研究的热点方向。除Graph-MLP模型,Wang等[16]提出了基于集群感知监督对比损失的ClusterSCL,ClusterSCL以节点聚类分布的形式保留图信息。Xia等[17]提出了一种无需数据增强的GNN对比学习框架SimGRACE,SimGRACE使用GNN编码器和扰动GNN编码器提取原始图特征,然后通过对比两个视图来保留关键的语义信息。此外,Wang等[18]对图对比学习中的结构公平性进行了探究,其研究结果表明引入对比学习后学习到的高度节点和低度节点的特征表示均优于GCN模型。
本文提出了一种基于属性信息和拓扑信息引导的图多层感知机模型,通过计算属性相似度和拓扑相似度,推动特征空间中相似节点的低维表示相互靠近,不相似节点的低维表示进一步远离,从而提升模型在节点分类任务上的表现。
2 A&T-MLP本节主要介绍A&T-MLP的算法原理及模型构建。首先提出模型整体架构,然后介绍用于对比损失的属性相似度和拓扑相似度,接着讨论用于模型训练的对比损失和交叉熵损失,最后介绍模型的优化过程。
2.1 模型结构MLP通过全连接层(Fully Connected Layer, FC)提取数据中蕴含的潜在信息,生成用于下游任务的特征表示。A&T-MLP在MLP的基础上,通过引入兼顾节点属性相似度与拓扑结构相似度的对比损失以增强模型对原始图信息的表征能力,其整体结构如图 1所示。由于过多的神经网络层数易导致模型过拟合[19],因此A&T-MLP使用3层网络结构。首先,使用MLP提取属性矩阵X的特征,在第1层和第2层网络之间引入激活函数ReLU和Dropout机制,这样不仅能增强模型的非线性变换能力,还能防止参数过拟合;然后,使用属性和拓扑信息引导的对比损失,对第2层网络生成的特征向量进行优化,使属性和拓扑相似的节点在特征空间中进一步接近,不相似的节点进一步远离;最后,使用第3层网络生成的特征向量计算交叉熵损失,从而实现节点分类任务。综上,A&T-MLP的网络结构可表示为
| $ \boldsymbol{H}^{(1)}=\operatorname{Dropout}(\operatorname{ReLU}(\mathrm{FC}(\boldsymbol{X}))), $ | (2) |
| $ \boldsymbol{H}^{(2)}=\operatorname{ReLU}\left(\operatorname{FC}\left(\boldsymbol{H}^{(1)}\right)\right), $ | (3) |
| $ \boldsymbol{Z}=\mathrm{FC}\left(\boldsymbol{H}^{(2)}\right)。$ | (4) |

|
| 图 1 A&T-MLP的框架 Fig. 1 The framework of A&T-MLP |
2.2 属性相似度与拓扑相似度
为了充分保留原始图中蕴含的属性与拓扑关联信息,分别使用节点属性矩阵X和邻接矩阵A计算用于对比损失函数的节点相似度。
对于拓扑结构,可以通过图的一阶相似度进行表示,即直接相连的节点关系更加紧密[20]。如果节点i和j之间存在1条边,那么i和j的一阶相似度为边的权重值(无权图中,权重值默认为1),如果i和j之间没有边,那么两个节点的一阶相似度为0。由于上述边信息通常使用图的邻接矩阵A进行存储,所以A中元素Aij能够直接表示节点i和j的拓扑相似度。
对于节点属性,属性矩阵X中元素Xij表示节点i和属性j之间的关联信息,不能直接表示节点间的相似度。因此,属性相似度计算的关键在于如何表示节点在属性空间的相似性,并通过与拓扑相似度相同的形式进行表示。首先,使用相似性度量算法,计算两个节点的属性相似性值Sij,本文使用余弦相似度获取相似度矩阵S。
余弦相似度即使用两个向量之间夹角的余弦值度量相似度:
| $ \mathit{\boldsymbol{S}}_{i j}=\frac{\mathit{\boldsymbol{x}}_i \cdot \mathit{\boldsymbol{x}}_j}{\left|\mathit{\boldsymbol{x}}_j\right|\left|\mathit{\boldsymbol{x}}_j\right|}, $ | (5) |
式中,xi和xj表示节点i和j的属性向量。根据S中数据元素大小为每个节点选取前k个最相似的节点并保留相似度值(其余位置为0),构建属性相似度矩阵S(k),此时S(k)中元素Sij(k)能够直接表示节点i和j的属性相似度。
拓扑相似度和属性相似度分别通过邻接矩阵A和属性相似度矩阵S(k)表示,但是A中元素Aij的取值为0, 1,S(k)中元素Sij(k)的取值为0, 1。为了消除两类不同信息在量纲和数值上的差异,对数据进行规范化处理Ã=D1-1A,
| $ \gamma=\tilde{\boldsymbol{A}}+\tilde{\boldsymbol{S}}^{(k)}, $ | (6) |
式中,γ表示包含原始图中属性与拓扑相似信息的节点关联强度矩阵。
2.3 损失函数在MLP提取数据特征生成节点表示的过程中,使用属性和拓扑引导信息γ计算对比损失可以推动特征空间中相似节点的低维表示彼此接近,不相似节点的低维表示进一步远离。基于对比损失的一般形式[公式(1)],A&T-MLP使用的对比损失lossCL表达式为
| $ \begin{array}{l} \quad\quad \operatorname{loss}_{C L}= \\ -\log \frac{\sum\nolimits_{j=1}^N \mathbf{1}_{[j \neq i]} \gamma_{i j} \exp \left(\operatorname{sim}\left(h_i, h_j\right)\right)}{\sum\nolimits_{k=1}^N \mathbf{1}_{[k \neq i]} \exp \left(\operatorname{sim}\left(h_i, h_k\right)\right)}, \end{array} $ | (7) |
式中,sim表示余弦相似度函数,h表示节点。lossCL借助节点的相似度信息以增大特征空间中相似节点的一致性和增大不相似节点的差异性。由于A&T-MLP是用于分类任务的模型,因此在训练过程中引入交叉熵损失lossCE:
| $ \operatorname{loss}_{C E}=-\sum\limits_{i \in \boldsymbol{Y}} \sum\limits_{m=1}^M Y_{i m} \log \left(Z_{i m}\right) $ | (8) |
式中,Y为节点标签集合,M为标签的类别数,Yim为符号函数(样本i的真实类别等于m则取值1,否则取0),Zim表示观测样本i属于类别m的预测概率。最后,将对比损失lossCL和交叉熵损失lossCE进行组合,构建完整的损失函数loss:
| $ \text { loss }=\operatorname{loss}_{C E}+\alpha \operatorname{loss}_{C L} \text {, } $ | (9) |
式中,α表示平衡lossCL和lossCE的加权系数。在确定网络结构和损失函数后,A&T-MLP优化的具体过程见算法1。
算法1 A&T-MLP
输入:属性矩阵X,邻接矩阵A,节点标签集合Y,隐藏层维度d、属性相似节点数k,权重系数α,可训练参数θ。
输出:模型优化参数θ。
1.计算属性矩阵X的余弦相似度得到相似度矩阵S
2.选取每个节点前k个相似度值构建属性相似度矩阵S(k)
3.对A和S(k)进行归一化,计算对比损失引导信息γ
4. Repeat
5. 使用X、θ和公式(3)、(4)生成特征矩阵H(2)和Z
6. 使用H(2)、Z、γ、α和公式(9),计算loss
7. 计算损失函数梯度▽loss,利用反向传播更新参数矩阵θ
8.Until convergence
3 结果与分析 3.1 实验设置本文使用3个基准图数据集Wikipedia、Cora和Citeseer[21]评估基线模型和A&T-MLP在节点分类任务中的实验性能,使用的基线模型和构建的基线模型均使用Python语言和深度学习框架Pytorch实现。数据集相关统计信息见表 1。基线模型分别选择GNN模型GCN[3]、SGC[4]、GAT[5]和GATv2[6],以及感知机模型MLP[10]和Graph-MLP[14]。
| 数据集 Dataset |
#节点 #Nodes |
#边 #Edges |
#属性 #Attributes |
#标签 #Labels |
| Wikipedia | 2 405 | 17 981 | 4 973 | 19 |
| Cora | 2 708 | 5 429 | 1 433 | 7 |
| Citeseer | 3 327 | 4 732 | 3 703 | 6 |
节点分类是一种多分类任务,利用图的拓扑结构和节点属性确定每个节点所属类别,因此采用常见多分类指标Micro-F1和Macro-F1进行评估。对于每个数据集,各模型采用相同数据集划分,随机抽取10%的节点标签作为训练集,剩余节点标签中随机抽取50%作为测试集。
所有基线模型都先按照原始论文中建议的参数进行初始化,然后对部分模型进一步调整,以获取最佳性能。对于A&T-MLP,参数主要包括学习率lr、训练次数epoch、隐藏层维度d、属性相似节点数k以及平衡损失函数的权重系数α。A&T-MLP的最终参数设置如表 2所示。
| 数据集 Dataset |
学习率 Learning rate (lr) |
训练次数 Epoch |
隐藏层维度 Dimension of hidden layers (d) |
属性相似节点数 Number of nodes with similar attributes (k) |
权重系数 Weighting coefficient (α) |
| Wikipedia | 10-2 | 150 | 512 | 30 | 6 |
| Cora | 10-3 | 500 | 512 | 20 | 10 |
| Citeseer | 10-3 | 400 | 512 | 30 | 10 |
3.2 实验结果
本节通过节点分类任务评估不同模型的实验性能,实验结果如表 3所示。从表 3可以看出,在3个数据集上,A&T-MLP模型的Micro-F1和Macro-F1分数始终高于基线模型,表明A&T-MLP能够有效保留原始图的属性和拓扑特征信息,并将其编码到节点特征向量中,从而提升了节点分类能力。在属性信息丰富的Wikipedia数据集上,所有GNN模型表现均弱于MLP模型,同时引入拓扑对比损失的Graph-MLP弱于仅使用属性信息的MLP。这表明在以属性为主要信息的数据集上,依赖拓扑结构进行特征提取和保留的方法限制了模型的表征能力,而同时使用属性和拓扑信息引导对比损失的A&T-MLP表现最好,能够有效平衡特征向量中蕴含的属性和拓扑信息。在拓扑信息丰富的Cora和Citeseer数据集上,所有GNN模型优于仅使用属性信息的MLP。GNN模型的高性能得益于信息传递和聚合过程中拓扑信息的重复使用,Graph-MLP则是通过对比损失保留了拓扑关联信息,而A&T-MLP的对比损失在关注拓扑相似性的同时,也对属性相似性这一重要的原始图信息进行关注,能够更为充分地保留分类任务所需的特征信息。
| Unit: % | |||||||||||||||||||||||||||||
| 模型 Model |
Wikipedia | Cora | Citeseer | ||||||||||||||||||||||||||
| Micro-F1 | Macro-F1 | Micro-F1 | Macro-F1 | Micro-F1 | Macro-F1 | ||||||||||||||||||||||||
| GCN | 56.83 | 41.11 | 76.37 | 75.18 | 71.42 | 64.44 | |||||||||||||||||||||||
| SGC | 53.13 | 35.19 | 74.74 | 73.15 | 67.64 | 60.45 | |||||||||||||||||||||||
| GAT | 55.33 | 39.49 | 76.07 | 74.75 | 70.47 | 64.34 | |||||||||||||||||||||||
| GATv2 | 54.71 | 37.38 | 73.41 | 71.45 | 72.45 | 65.56 | |||||||||||||||||||||||
| MLP | 69.07 | 49.73 | 61.60 | 54.93 | 64.72 | 54.79 | |||||||||||||||||||||||
| Graph-MLP | 67.84 | 49.15 | 78.73 | 75.03 | 74.43 | 67.69 | |||||||||||||||||||||||
| A&T-MLP | 72.69 | 54.75 | 82.79 | 81.31 | 76.70 | 70.09 | |||||||||||||||||||||||
| Note: bold is the best result, underlined is the second best result. | |||||||||||||||||||||||||||||
综上,不同基线模型在不同数据集上的表现差异较大,并且复杂的信息传递和聚合方式不一定能够获得最佳的性能。相较于基线模型,A&T-MLP在不同数据集上均能获得最佳性能,证明了同时使用属性和拓扑相似度信息引导的对比损失,不仅能够提升模型的预测性能,而且也增强了模型对不同数据的泛化能力。
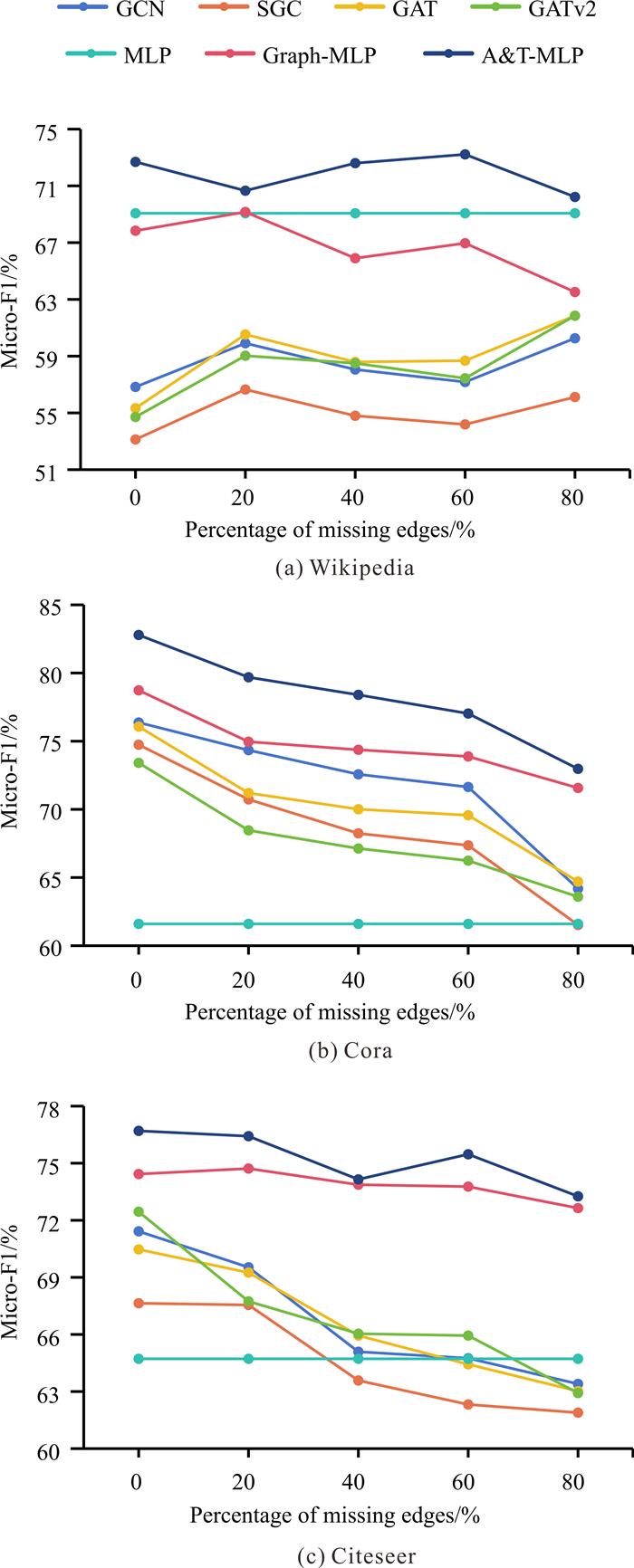
为了进一步探究A&T-MLP在3个数据集上的性能,本文通过减少训练集中边缘的数量评估基线模型和A&T-MLP在信息缺失条件下的实验表现。在边缘缺失实验中,每次减少训练集中20%的边信息,实验结果见图 2。
|
| 图 2 边缘缺失实验结果 Fig. 2 Results of the missing edge experiment |
由图 2可知,随着训练集中包含的边信息不断减少,各模型的实验性能出现较为明显的波动(由于MLP仅使用属性信息,实验结果不受边信息减少影响),但A&T-MLP模型的预测结果始终优于其他基线模型。在属性信息丰富的Wikipedia数据集上,边信息的减少不一定导致模型性能下降,相反GNN模型在边缘缺失80%时取得了最佳实验结果。在拓扑信息丰富的Cora和Citeseer数据集上,除MLP外所有模型的实验性能随边信息的减少呈现出下降趋势,特别是GATv2在边缘缺失80%时性能下降9.53%。综上,在边信息大量缺失时A&T-MLP相较基线模型能够更好地学习数据特征分布,改善节点分类任务的实验表现。
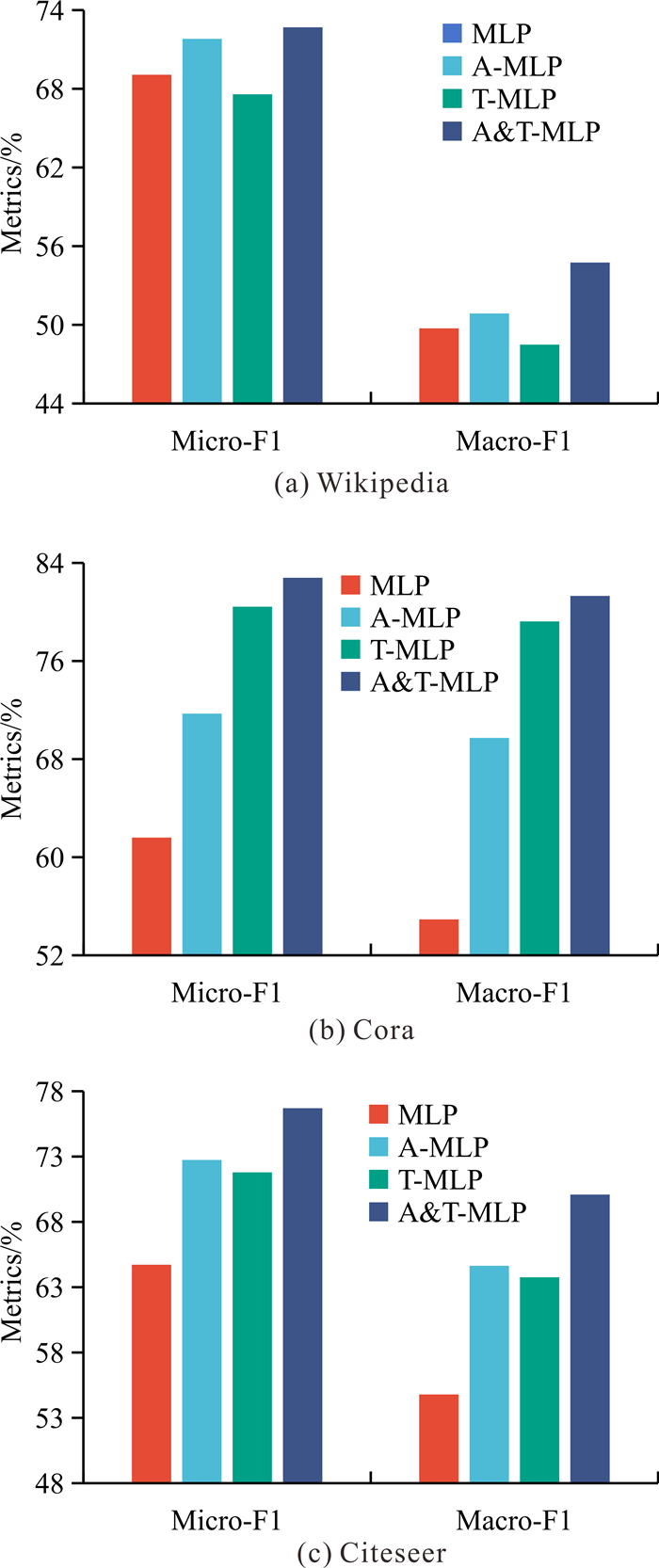
3.3 消融实验为了验证拓扑信息和属性信息对A&T-MLP模型性能的影响,在3个数据集上进行消融实验,记录Micro-F1和Macro-F1。其中,不使用对比损失的变体为MLP,仅使用拓扑信息引导对比损失的变体为T-MLP,仅使用属性信息引导对比损失的变体为A-MLP。为保证实验结果的公平性,保持各模型参数一致。消融实验结果如图 3所示。相较于不使用原始图信息、单独使用拓扑信息或属性信息的变体,同时使用两类信息的A&T-MLP模型获得了最佳性能,证明同时保留属性和拓扑信息能够进一步增强模型的表征能力,提升分类任务中的实验表现。
|
| 图 3 消融实验结果 Fig. 3 Results of ablation experiment |
3.4 参数实验
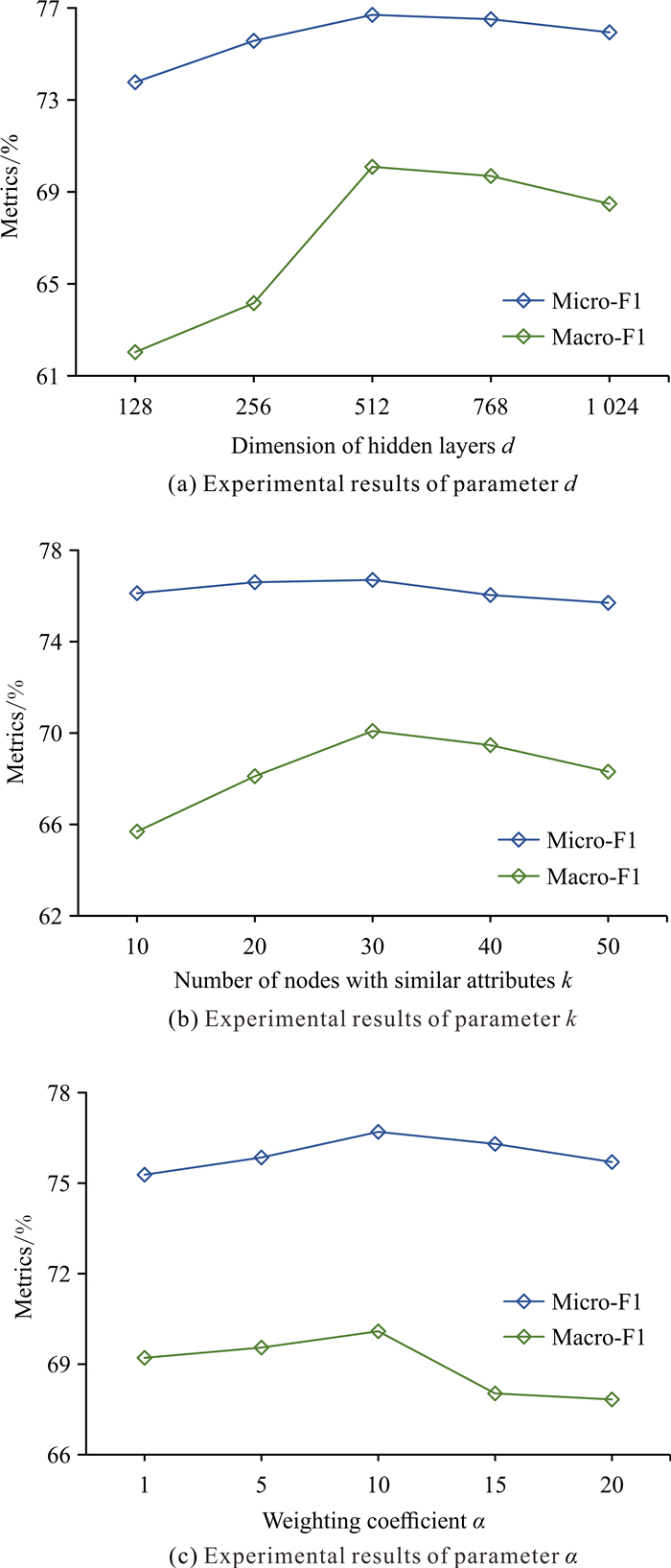
为了分析A&T-MLP性能受参数的影响,使用Citeseer数据集进行参数实验,并记录Micro-F1和Macro-F1分数。此外,为了保证参数实验的公平性,除验证参数外,其余参数按照表 3进行设置。参数实验结果如图 4所示。
|
| 图 4 参数实验结果 Fig. 4 Results of parametric experiment |
为了验证隐藏层维度d对A&T-MLP性能的影响,使用不同d值进行实验,结果如图 4(a)所示。最初,Micro-F1和Macro-F1随网络维度的增大而提高,这是因为较高的维度代表了更多的神经元,能够编码更多的有益信息,提升实验表现。但是,随着维度进一步增大,Micro-F1和Macro-F1呈现出下降的趋势,这是因为过大的维度使节点表示中编码了噪声信息,从而影响了A&T-MLP的表现。
为了验证属性相似节点数k对A&T-MLP性能的影响,使用不同k值进行实验,结果如图 4(b)所示。从结果看,Micro-F1和Macro-F1呈现先上升再下降的趋势,过大和过小的k值下A&T-MLP的表现均较为一般,这是因为k值过小无法保留充足的属性相似度信息,而k值过大会在对比损失计算过程中引入大量噪声节点,影响A&T-MLP的性能。
为了验证损失函数中的权重系数α对模型性能的影响,使用不同α值进行实验,结果如图 4(c)所示。权重系数α调控了对比损失在整个损失函数中所占的比重,α值越大模型训练过程中越关注对比损失的优化。从实验结果来看,A&T-MLP的预测性能随着α值的增大先上升后下降,这是因为过于关注对比损失的优化会导致对交叉熵损失的忽略,从而影响了A&T-MLP的性能。
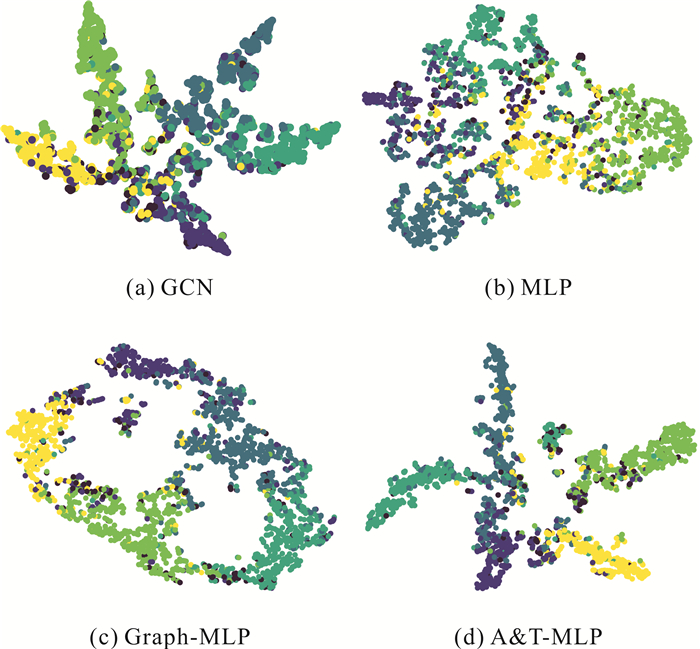
3.5 可视化节点表示蕴含了原始图的相关信息,对其进行可视化能够直观地反映原始图的某些特征。对于可视化任务,首先使用t-SNE[22]将各模型生成的节点特征向量降至2维,然后根据Citeseer数据集的标签信息将节点分别标记为6种颜色,最后在二维平面上进行可视化,实验结果如图 5所示。节点分类准确的可视化结果通常为相同颜色节点接近,不同颜色节点远离。由图 5可知,GCN、MLP、Graph-MLP和A&T-MLP均能提取原始图中相关信息形成社区结构,但是使用属性和拓扑信息引导对比损失的A&T-MLP具有更高的类内相似性和类间界限。可视化实验反映了模型保留同一社群节点相似特征的能力,证明了使用对比损失能够增强模型表征能力,也更为直观地反映了模型的分类性能。
|
| 图 5 Citeseer可视化 Fig. 5 Visualization of Citeseer |
3.6 训练时间
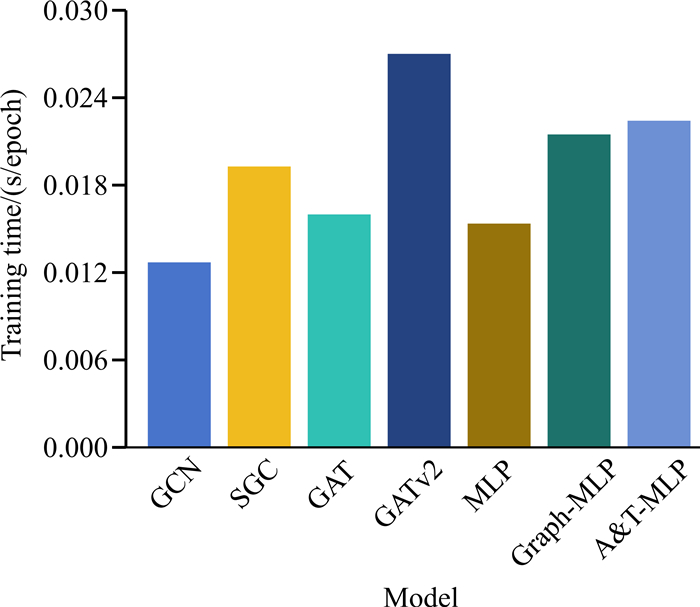
为了比较不同模型的训练复杂度,记录Wikipedia数据集上迭代100次后单次迭代的平均训练时间(包括前向传播、损失函数计算、反向传播过程),实验结果如图 6所示。对比不同模型的训练时间,直接对原始图信息编码的GCN和MLP计算速度较快,在此基础引入了更加复杂的特征提取方式的改进模型训练时间进一步增加。虽然基于MLP的改进模型网络结构更为简单,但是为了保留原始图相关信息,需要借助对比损失进行优化,导致模型的训练时间增加。此外,对比使用对比损失的Graph-MLP和A&T-MLP,尽管A&T-MLP引入了属性信息,但是只保留了每个节点前k个相似度值最大的值,因此相较于GAT和GATv2训练时间差异较大,相较于Graph-MLP训练时间差异较小,并且实验性能提升更为明显。
|
| 图 6 训练时间对比 Fig. 6 Comparison of training time |
4 结论
本文设计了一种无需信息传递和聚合的图多层感知机模型A&T-MLP,通过属性和拓扑信息引导的对比损失有效保留原始图特征。实验结果表明,基于属性相似度与拓扑相似度的对比损失能够显著提升MLP模型在节点分类任务中的实验性能,并且优于较为先进的GNN基线模型。此外,A&T-MLP在处理拓扑信息不准确的图数据时具有较明显的优势,即使在拓扑信息缺失80%的极端情况下,依然具有良好的性能。在当前工作中,通过简单的MLP构建神经网络基本框架,使得模型训练过程中缺乏对特征中重要信息的关注。因此,在后续工作中,将在多层神经网络中引入注意力机制,增强关键特征信息的保留,并将模型应用于社交网络恶意账户检测和犯罪组织成员身份发现等任务。
| [1] |
ZOU M H, GAN Z X, CAO R Z, et al. Similarity-navigated graph neural networks for node classification[J]. Information Sciences, 2023, 633: 41-69. DOI:10.1016/j.ins.2023.03.057 |
| [2] |
VELIČKOVIĆ P. Everything is connected: graph neural networks[J]. Current Opinion in Structural Biology, 2023, 79: 102538. DOI:10.1016/j.sbi.2023.102538 |
| [3] |
BHATTI U A, TANG H, WU G L, et al. Deep learning with graph convolutional networks: an overview and latest applications in computational intelligence[J]. International Journal of Intelligent Systems, 2023, 2023: 8342104. |
| [4] |
YANG F, ZHANG H Y, TAO S M. Simplified multilayer graph convolutional networks with dropout[J]. Applied Intelligence, 2022, 52: 4776-4791. DOI:10.1007/s10489-021-02617-7 |
| [5] |
HE L C, BAI L, YANG X, et al. High-order graph attention network[J]. Information Sciences, 2023, 630: 222-234. DOI:10.1016/j.ins.2023.02.054 |
| [6] |
BRODY S, ALON U, YAHAV E. How attentive are graph attention networks? [C]//Proceedings of the 2022 International Conference on Learning Representations (ICLR 2022). Virtual: OpenReview, 2022: 1-26.
|
| [7] |
SUN Y F, DENG H R, YANG Y, et al. Beyond homophily: structure-aware path aggregation graph neural network [C]//Proceedings of the 2022 International Joint Conference on Artificial Intelligence (IJCAI-22). San Francisco: Morgan Kaufmann, 2022: 2233-2240.
|
| [8] |
WU G C, LIN S K, SHAO X X, et al. QPGCN: graph convolutional network with a quadratic polynomial filter for overcoming over-smoothing[J]. Applied Intelligence, 2023, 53: 7216-7231. DOI:10.1007/s10489-022-03836-2 |
| [9] |
ZHANG A C, HUANG J C, LI P, et al. Building shortcuts between distant nodes with biaffine mapping for graph convolutional networks [EB/OL]. (2023-02-17)[2023-09-01]. https://arxiv.org/pdf/2302.08727.pdf.
|
| [10] |
KRUSE R, MOSTAGHIM S, BORGELT C, et al. Multilayer perceptrons [M]//Computational Intelligence: a methodological introduction. Cham: Springer, 2022: 53-124.
|
| [11] |
HOU Q B, JIANG Z H, YUAN L, et al. Vision permutator: a permutable MLP-like architecture for visual recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(1): 1328-1334. DOI:10.1109/TPAMI.2022.3145427 |
| [12] |
GONG N, ZHANG C L, ZHOU H, et al. Classification of hyperspectral images via improved cycle-MLP[J]. IET Computer Vision, 2022, 16: 468-478. DOI:10.1049/cvi2.12104 |
| [13] |
SUN H, WANG H Y, LIU J Q, et al. CubeMLP: an MLP-based model for multimodal sentiment analysis and depression estimation [C]//Proceedings of the 30th ACM International Conference on Multimedia. Lisbon, Portugal: ACM, 2022: 3722-3729.
|
| [14] |
HU Y, YOU H X, WANG Z C, et al. Graph-MLP: node classification without message passing in graph [EB/OL]. (2021-06-08)[2023-09-01]. https://arxiv.org/pdf/2106.04051.pdf.
|
| [15] |
RANI V, NABI S T, KUMAR M, et al. Self-supervised learning: a succinct review[J]. Archives of Computational Methods in Engineering, 2023, 30: 2761-2775. DOI:10.1007/s11831-023-09884-2 |
| [16] |
WANG Y L, ZHANG J, LI H Y, et al. ClusterSCL: cluster-aware supervised contrastive learning on graphs [C]//Proceedings of the 2022 ACM Web Conference. Lyon, France: ACM, 2022: 1611-1621.
|
| [17] |
XIA J, WU L R, CHEN J T, et al. SimGRACE: a simple framework for graph contrastive learning without data augmentation [C]//Proceedings of the 2022 ACM Web Conference. Lyon, France: ACM, 2022: 1070-1079.
|
| [18] |
WANG R J, WANG X, SHI C, et al. Uncovering the structural fairness in graph contrastive learning [C]// 36th Conference on Neural Information Processing Systems (NeurIPS 2022). New Orleans, USA: MIT Press, 2022: 32465-32473.
|
| [19] |
WANG R Q, ZHU F, ZHANG X Y, et al. Training with scaled logits to alleviate class-level over-fitting in few-shot learning[J]. Neurocomputing, 2023, 522: 142-151. DOI:10.1016/j.neucom.2022.12.011 |
| [20] |
袁立宁, 蒋萍, 莫嘉颖, 等. 基于二阶图卷积自编码器的图表示学习[J/OL]. 计算机工程与应用, 2023: 1-9. [2023-10-10]. http://kns.cnki.net/kcms/detail/11.2127.TP.20230626.1839.016.html.
|
| [21] |
WAIKHOM L, PATGIRI R. A survey of graph neural networks in various learning paradigms: methods, applications, and challenges[J]. Artificial Intelligence Review, 2023, 56: 6295-6364. DOI:10.1007/s10462-022-10321-2 |
| [22] |
WANG Y F, HUANG H Y, RUDIN C, et al. Understanding how dimension reduction tools work: an empirical approach to deciphering t-SNE, UMAP, TriMAP, and PaCMAP for data visualization[J]. Journal of Machine Learning Research, 2021, 22: 1-73. |



