2. 南宁学院, 中国-东盟综合交通国际联合实验室, 广西南宁 530200
2. China-ASEAN International Join Laboratory of Integrate Transport, Nanning University, Nanning, Guangxi, 530200, China
在传统的蜂窝网络中,随着计算密集型移动应用的激增,用户的服务请求随之增加。为了有效满足移动互联网、物联网高速发展所需的高回传带宽、低能耗的要求,业界提出了移动边缘计算(Mobile Edge Computation,MEC)技术[1]。MEC技术的特点是将远端云的网络资源下沉至网络边缘,使用户可以近距离地使用边缘节点的网络资源。在一些应用场景(如增强/虚拟现实、动态内容交付、物联网、车联网等)中,人们在蜂窝网络边缘部署MEC服务器,将移动设备中的计算任务卸载到MEC服务器上进行存储、计算,从而解决移动设备在资源存储、计算性能以及能效等方面的不足。任务卸载作为MEC中关键技术之一,可以将资源受限的移动设备部分或者全部任务交给云计算环境处理,从而降低能耗,提高任务执行效率。
目前,MEC任务卸载重点研究3种卸载决策:本地执行、完全卸载和部分卸载。其中,本地执行是移动设备在本地执行任务,需要消耗设备本身资源和能量;完全卸载即二进制卸载则是将任务全部卸载到资源充足的服务器或移动设备上;部分卸载是按照一定的策略将一部分任务卸载到服务器执行,一部分则在本地执行。已有研究提出以降低能量消耗为目标的卸载策略[2-5]。You等[2, 3]考虑了由多个用户组成的MEC卸载系统的资源分配问题,并进一步研究了基于时分多址(Time Division Multiple Access,TDMA)和正交频分多址(Orthogonal Frequency Division Multiple Access,OFDMA)的多用户MEC卸载系统的资源分配问题,采用优先级与阈值相比较的方法决定卸载策略。Ali等[4]基于深度学习的智能决策算法,提出了一种新颖的、基于高效节能深度学习的卸载方案。薛建彬等[5]针对一对多的广播系统任务分配问题,设计了一种基于拉格朗日乘子法的任务分配优化算法,对用户本身和不同参数的接入点进行合理的任务分配,以联合优化任务分配和执行时延,实现系统开销最小化。
MEC任务卸载使得任务执行性能增强,但是当多个移动用户设备同一时刻卸载任务到服务器时,MEC服务器上可能会发生资源争用的问题;同时,当移动设备远离基站时,设备自身资源不足,任务也不能卸载到基站。设备间(Device to Device,D2D)通信技术被认为是应对上述问题有效的技术。D2D通信技术是指通信网络中邻近设备之间直接交换信息的技术,可以降低通信系统中核心网络的数据压力,提高频谱效率和吞吐量。近年来,D2D通信技术和MEC技术的结合应用在提高蜂窝网络频谱效率和能源效率方面得到了广泛的研究。Chai等[6]研究了一个蜂窝-D2D-MEC系统任务执行代价最小化问题,提出一个联合任务管理体系来实现高效的信息交互和任务管理。考虑利用邻近策略来支持高速移动计算和高速数据通信,He等[7]结合MEC和D2D通信技术来提高蜂窝网络的计算能力,最大限度地提高支持设备任务执行的数量。Kai等[8]研究了D2D通信辅助MEC网络中计算联合资源管理问题,通过D2D通信显著增加了MEC网络中执行的任务数,且大大降低了每个执行任务的能耗。上述研究专注于移动设备的能效,并未考虑利用无线携能通信(Simultaneous Wireless Information and Power Transfer, SWIPT)技术同时给移动设备传输信息和提供能量的特点,从而在满足移动设备所需能源供应的同时提高实时计算能力。
由于移动设备电池容量有限,在没有电源的情况下移动设备无法长时间工作。传统的移动设备由普通的电池供电,在使用中需要频繁更换电池或充电,使得这些设备在无线通信过程中常常发生任务处理中断,一方面给设备通信带来不必要的麻烦,另一方面会产生昂贵的电池更换成本,给环境带来巨大的污染。基于射频(Radio Frequency,RF)信号的SWIPT技术可以对RF信号进行能量收集(Energy Harvesting,EH),具有更高的可控性和稳定性[9]。基于SWIPT技术的EH设备有两种接收机模式,即时间切换(Time Switching,TS)和功率分流(Power Splitting,PS)[10]。TS模式下的EH和信息解码(Information Decoding,ID)处于不同时隙;PS模式则将接收到的信号分成不同功率信号,同时进行EH和ID。这两种接收模式使SWIPT技术能够应用于各种MEC网络,克服网络中移动用户的电池性能瓶颈。目前已有将SWIPT技术应用到MEC系统中的研究,Wen等[11]提出了一个基于多输入多输出(Multiple Input Multiple Output,MIMO)全双工中继的SWIPT-MEC系统,在保证移动用户能量充足的情况下降低系统总能耗。与之不同的是,Chen等[12]提出的框架中没有中继节点,将资源分配作为一个联合的非线性优化问题,以期达到最小化系统总能耗的目标。Fu等[13, 14]针对车联网和卫星物联网两个场景,模拟单个部署有MEC服务器的基站与多个用户之间的无线通信过程,其中车联网场景的研究目标是最小化设备的能耗,而卫星物联网场景则是最大化终端的上行传输速率。上述研究主要考虑将任务卸载到MEC服务器,然而,随着应用场景的不断丰富,在最大可容忍时延约束下MEC服务器的计算资源将无法满足大量的计算需求。
目前将MEC技术和SWIPT技术结合,可在一定范围内实现通信网络系统的增益,解决通信系统中移动用户计算能力不足以及无线资源缺乏问题,提高系统的计算能力和续航能力。考虑到大量计算密集型任务卸载到MEC服务器可能会发生资源争用,可以借助D2D通信将任务卸载给邻近设备,从而缓解MEC服务器的计算压力。本文构建一个基于SWIPT的多用户D2D通信辅助的MEC系统模型,采用SWIPT技术将基站的RF信号传输给移动用户,移动用户均配置PS接收机对接收的RF信号进行信息解码和能量收集;同时,提出一种D2D-MEC联合任务卸载策略,该策略采用二进制卸载模式,移动用户可以选择本地执行、MEC卸载和D2D卸载3种策略中的任意1种,拟通过联合优化功率分配和任务卸载问题,实现请求用户总能耗最小化的目标。
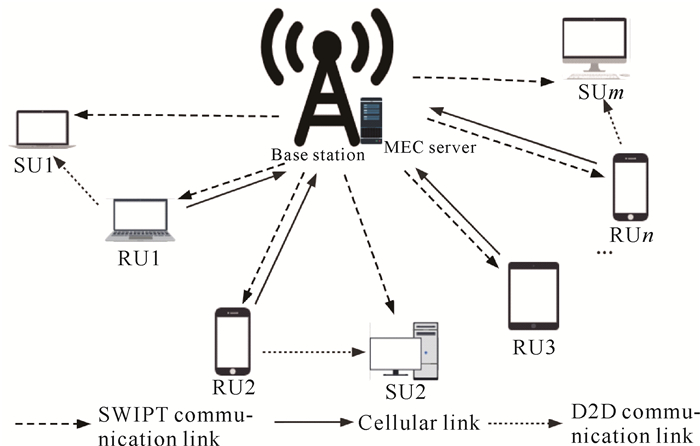
1 系统模型本文考虑如图 1所示的一个基于SWIPT的多用户D2D通信辅助MEC系统。该系统由单个部署了MEC服务器的基站(Base Station,BS)、N个需要执行计算任务的请求用户(Request Users,RUs)以及M个空闲的服务用户(Service Users,SUs)组成。移动用户都是单天线,基站是多天线。每个请求用户RU都有一个计算密集型任务,该任务可以表示为
|
| 图 1 基于SWIPT的多用户D2D通信辅助的MEC系统 Fig. 1 Multi-user D2D communication assisted MEC system based on SWIPT |
系统中每个请求用户RUi(i=1, 2, …, N)既可以与基站建立蜂窝链路,也可以与一个且仅一个邻近的服务用户SUj(j=1, 2, …, M)建立D2D通信链路。RUs既可以通过蜂窝链路将计算任务卸载到MEC服务器,也可以通过D2D通信链路将计算任务卸载到某些性能相对较高且空闲的SUs上,SUs为邻近的请求用户提供D2D卸载服务。总的来说,RUi可以在3种模式下执行任务,即本地执行、MEC卸载、D2D卸载,不能接收其他用户的任务进行求解。为了保证执行任务的安全性,假设RUi的任务不可拆分,每个任务只能选择一种计算模式执行。由于MEC服务器的计算资源丰富,任务优先选择MEC卸载模式,只有当MEC服务器在最大可容忍时延内执行的任务达到上限时,再考虑选择D2D卸载模式;当所有服务用户都被占用时,最后考虑在本地执行。
BS配有多输入多输出天线、强大的计算芯片和充电设备[15]。在该系统中,为了最大限度地扩大蜂窝网络待执行计算密集型任务的设备范围,它需要在最大可容忍时延下处理RUs上传的所有计算任务,然后通过子信道返回计算结果和能量。
1.1 能量收集模型为了保证系统中每个移动用户(Mobile Users,MUs)不会因能量不足而造成任务执行中断,假设每个MU都配备了一个PS接收机,PS接收机将基站传输的射频信号按照一定的比率分成两个不同的功率流,接收信号的ρ部分用于能量收集,(1-ρ)部分用于信息解码[16],功率分流架构如图 2所示。为了保证终端的功率不被消耗,本文采用下行最大功率向终端传输能量。

|
| 图 2 SWIPT中的功率分流架构 Fig. 2 Power splitting architecture in SWIPT |
MUk(k=1, 2, …, N+M)接收到的最大能量[6]可以表示为
| $ E_k^{\mathrm{eh}}=\rho \beta_k\left(P_k^{\mathrm{eh}} h_k^{\text {eh }} T^{\text {tolerant }}+\sigma^2\right), $ | (1) |
式(1)中,βk表示MUk的能量转换率,Pkeh表示基站到MUk之间的下行最大传输功率,hkeh则表示基站与MUk之间用于能量传输的信道增益,Ttolerant表示下行最大可容忍时延,σ2表示高斯白噪声功率。由于终端需要不断地接收能量,因此假设信道增益在一段时间内保持不变[16],且这些信道是固定的。
1.2 任务执行模型为了降低请求用户总能耗,RUi可以采取3种任务执行模式中的任意1种,任务执行模型如图 3所示。

|
| 图 3 任务执行模型 Fig. 3 Task execution model |
1.2.1 本地执行
Tilocal表示RUi本地执行任务的时延[17],用公式表达为
| $T_i^{\text {local }}=\frac{D_i}{F_i}, $ | (2) |
式(2)中,Di表示完成任务所需的计算资源量,Fi表示RUi的计算能力(1≤i≤N)。本文中,RUi、SUj和MEC服务器的计算能力被定义为设备或服务器的CPU运行频率。
RUi本地执行任务消耗的能量为[13]
| $E_i^{\text {local }}=\kappa D_i F_i^2, $ | (3) |
式(3)中,κ表示与设备的CPU性能相关的有效开关电容。
1.2.2 MEC卸载执行在MEC卸载模式下执行任务,完成任务的总时间包括任务上传时延、MEC服务器中任务执行时延以及基站将计算结果回传给RUi的时延。
Timec表示MEC卸载模式下RUi的任务执行时延,其计算公式为
| $T_i^{\mathrm{mec}}=T_i^{\mathrm{mec}, t}+T_i^{\mathrm{mec}, e}, $ | (4) |
式(4)中,Timec, t表示RUi将任务卸载到MEC服务器的传输时延;Timec, e表示任务在MEC服务器中的执行时延。由于MEC服务器上处理的任务输出数据量通常远小于输入数据量,所以忽略结果回传时间[11]。
Timec, t的计算公式如下:
| $ T_i^{\mathrm{mec}, t}=\frac{I_i}{R_i^{\mathrm{mec}}}, $ | (5) |
式(5)中,Ii表示RUi输入数据的大小;Rimec表示RUi向MEC服务器传输任务时的可完成数据速率,可以表示为
| $ R_i^{\mathrm{mec}}=W^b \log _2\left(1+\frac{p_i^{\mathrm{mec}} h_i}{\sigma^2}\right), $ | (6) |
式(6)中,Wb表示BS的信道带宽,pimec表示RUi到MEC服务器的上行传输功率,hi表示RUi到基站的信道增益。
式(4)中的Timec, e可以表示为
| $ T_i^{\mathrm{mec}, e}=\frac{D_i}{\theta_i F^{\mathrm{mec}}}, $ | (7) |
式(7)中,θi∈[0, 1],表示任务卸载到MEC服务器时分配给RUi的计算能力系数,Fmec为MEC服务器的计算能力。
RUi在MEC卸载模式下的传输能耗可以用上行传输功率与输入数据的大小的乘积与数据传输速率之比表示:
| $ E_i^{\mathrm{mec}}=\frac{p_i^{\mathrm{mec}} I_i}{R_i^{\mathrm{mec}}}。$ | (8) |
本文假设RUi自身由于信号处理而产生的能量消耗可以忽略,这里只研究RUi将其任务传输到MEC服务器而产生的能量消耗。
1.2.3 D2D卸载执行当RUi通过D2D通信链路将任务传输给SUj,D2D卸载执行任务的总时延Ti, jd2d为
| $ T_{i, j}^{\mathrm{d} 2 \mathrm{d}}=T_{i, j}^{\mathrm{d} 2 \mathrm{d}, t}+T_{i, j}^{\mathrm{d} 2 \mathrm{d}, e}, $ | (9) |
式(9)中,Ti, jd2d, t表示RUi将任务卸载到SUj所需的传输时延,Ti, jd2d, e表示任务在SUj处的执行时延。这里SUj的计算能力高于RUi的计算能力,有效地降低了任务完成总时延。Ti, jd2d, t、Ti, jd2d, e的计算公式分别为
| $ \begin{aligned} T_{i, j}^{\mathrm{d} 2 \mathrm{d}, t} =\frac{I_i}{R_{i, j}^{\mathrm{d} 2 \mathrm{d}}}, \end{aligned} $ | (10) |
| $ T_{i, j}^{\mathrm{d} 2 \mathrm{d}, e} =\frac{D_i}{F_j^{\mathrm{d} 2 \mathrm{d}}}, $ | (11) |
式(11)中,Fjd2d为SUj的计算能力;式(10)中,Ri, jd2d为RUi向SUj传输任务时的数据传输速率,可以表示为
| $ R_{i, j}^{\mathrm{d} 2 \mathrm{d}}=W^d \log _2\left(1+\frac{p_i^{\mathrm{d} 2 \mathrm{d}} h_{i, j}}{\sigma^2}\right), $ | (12) |
式(12)中,Wd和hi, j分别表示RUi与SUj之间的信道带宽和信道增益,pid2d表示RUi传输任务到SUj时的传输功率。
RUi上传任务到SUj的传输能耗为
| $E_{i, j}^{\mathrm{d} 2 \mathrm{d}, t}=p_i^{\mathrm{d} 2 \mathrm{d}} T_{i, j}^{\mathrm{d} 2 \mathrm{d}, t}, $ | (13) |
SUj执行RUi上传任务所消耗的能量为
| $ E_{i, j}^{\mathrm{d} 2 \mathrm{d}, e}=\kappa D_i\left(F_j^{\mathrm{d} 2 \mathrm{d}}\right)^2 。$ | (14) |
在上述系统模型的基础上,本文提出一种具有一系列必要约束条件的联合优化功率分配和任务卸载的请求用户总能耗最小化问题。
2.1 优化约束为了解决联合优化功率分配和任务卸载问题,使得请求用户总能耗最小,需要考虑一系列优化约束条件。
本文中,每个RUi只能选择本地执行、MEC卸载、D2D卸载3种任务卸载模式中的1种,用λilocal∈{0, 1}表示RUi的本地执行变量,即当RUi在本地执行任务时,λilocal=1,否则λilocal=0;λimec∈{0, 1}表示RUi的MEC卸载变量,即当RUi卸载其任务到MEC服务器时,λimec=1,否则λimec=0;λi, jd2d∈{0, 1}表示RUi的D2D卸载变量,即当RUi卸载其任务到SUj时,λi, jd2d=1,否则λi, jd2d=0。本文将任务卸载约束表示为
| $ \begin{aligned} & \mathrm{C} 1: \lambda_i^{\text {local }}+\lambda_i^{\text {mec }}+\sum\limits_{j=1}^M \lambda_{i, j}^{\mathrm{d} 2 \mathrm{d}}=1, \lambda_i^{\text {local }}, \lambda_i^{\text {mec }}, \lambda_{i, j}^{\mathrm{d} 2 \mathrm{d}} \in \\ & \{0, 1\}。\end{aligned} $ | (15) |
受传输和计算资源的限制,本文假设一个请求用户只能向一个服务用户发送D2D卸载服务,即
| $ \mathrm{C} 2: \sum\limits_{j=1}^M \lambda_{i, j}^{\mathrm{d} 2 \mathrm{d}} \leqslant 1 。$ | (16) |
为了保证RUs在执行任务卸载时维持高效的数据传输速率防止数据传输阻塞,假设单个RU的数据传输速率应不大于最大数据传输速率约束Rimax, 即当λilocal=0时,
| $ \mathrm{C} 3: \lambda_i^{\mathrm{mec}} R_i^{\mathrm{mec}}+\sum\limits_{j=1}^M \lambda_{i, j}^{\mathrm{d} 2 \mathrm{d}} R_{i, j}^{\mathrm{d} 2 \mathrm{d}} \leqslant R_i^{\max } 。$ | (17) |
在本文中,假设Rimax是一个给定常数,由用户任务的特性决定。每个请求用户卸载任务到MEC服务器以及服务用户的传输功率都受其最大上行功率的限制,即
| $ \begin{aligned} \mathrm{C} 4: p_i^{\mathrm{mec}} \leqslant p_{\max }^{\mathrm{mec}} , \end{aligned} $ | (18) |
| $ \mathrm{C} 5: p_i^{\mathrm{d} 2 \mathrm{d}} \leqslant p_{\max }^{\mathrm{d} 2 \mathrm{d}}。$ | (19) |
式(18)中pmaxmec表示RUi卸载任务到MEC服务器的最大上行传输功率,式(19)中pmaxd2d表示RUi卸载任务到SUj的最大上行传输功率。
为了提高用户的续航能力,所有移动用户通过SWIPT技术收集的能量必须大于其自身消耗的能量[18],具体约束表示为
| $ \begin{aligned} \mathrm{C} 6: \lambda_i^{\text {local }} E_i^{\text {local }}+\lambda_i^{\text {mec }} E_i^{\text {mec }}+\lambda_{i, j}^{\mathrm{d} 2 \mathrm{d}} E_{i, j}^{\mathrm{d} 2 \mathrm{d}, t} \leqslant E_i^{\mathrm{eh}}, \end{aligned} $ | (20) |
| $ \mathrm{C} 7: E_{i, j}^{\mathrm{d} 2 \mathrm{d}, e} \leqslant E_j^{\mathrm{eh}}, 1 \leqslant j \leqslant M 。$ | (21) |
式(20)中Eieh表示RUi收集的能量,式(21)中Ejeh表示SUj收集的能量。
在最大可容忍时延内所有RUs同时进行计算,系统总时延不超过Tmax,即
| $\begin{aligned} \mathrm{C} 8: 0 & \leqslant \sum\limits_{i=1}^N\left(\lambda_i^{\text {local }} T_i^{\text {local }}+\lambda_i^{\text {mec }} T_i^{\text {mec }}+\right. \\ \left.\sum\limits_{j=1}^M \lambda_{i, j}^{\mathrm{d} 2 \mathrm{d}} T_{i, j}^{\mathrm{d} 2 \mathrm{d}}\right) & \leqslant T^{\max } 。\end{aligned} $ | (22) |
本文的目标是在最大可容忍时延内,确保全部请求用户的计算任务能够成功计算的情况下,最小化请求用户总能耗。每个RU的能耗可能包括本地执行能耗、MEC卸载传输能耗、D2D卸载传输能耗。为了求解该数学问题,通过数学表达式得到目标函数Etotal为
| $\begin{aligned} & \quad E^{\mathrm{total}}=\sum\limits_{i=1}^N\left(\lambda_i^{\text {local }} E_i^{\text {local }}+\lambda_i^{\text {mec }} E_i^{\text {mec }}+\right. \\ & \left.\sum\limits_{j=1}^M \lambda_{i, j}^{\mathrm{d} 2 \mathrm{d}} E_{i, j}^{\mathrm{d} 2 \mathrm{d}, t}\right)_{\circ} \end{aligned} $ | (23) |
根据上述目标函数和优化约束条件,基于请求用户能耗最小化的联合任务卸载和功率分配优化问题可以表述为
| $ \text { P1 } \min\limits _{\lambda_i^{\text {local }}, \lambda_i^{\text {mec }}, \lambda_{i, j}^{\text {d2d }}, p_i^{\text {mec }}, p_i^{\text {d2d }}} E^{\text {total }} \text {, s. t. } \quad \mathrm{C} 1 \sim \mathrm{C} 8 \text { 。} $ | (24) |
问题P1中包含了整数变量λilocal、λimec、λi, jd2d和实数变量pimec、pid2d,是一个非线性混合整数规划问题,不便于直接求解。
2.3 问题求解针对优化问题P1,本文求解的思路如下:首先根据整数变量和实数变量将原问题解耦为两个子问题,即功率分配子问题和任务卸载子问题,然后再分别求解。
2.3.1 求解功率分配子问题由式(23)可知,Etotal由3部分组成,分别对应3种不同的计算卸载模式。因为本文研究的是请求用户的总能耗,所以Etotal不包括任务通过D2D卸载到SUj上执行所消耗的能量。由于Eimec, Ei, jd2d, t分别与变量pimec, pid2d有关,所以下面分别考虑MEC卸载模式和D2D卸载模式,求解能耗最小化问题。
在MEC卸载模式下,λilocal=0, λimec=1, λi, jd2d=0,RUs的总能耗最小化问题可以表示为
| $ \text { P2.1a } \min \limits_{p_i^{\text {mec }}} E_i^{\text {mec }} \text {, s. t. }~~~~ \mathrm{C} 3, \mathrm{C} 4, \mathrm{C} 6, \mathrm{C} 8 \text { 。} $ | (25) |
上述问题是一个非线性分数规划问题,是非凸的,同样很难直接获得最优解。本文利用典型的Dinkelbach方法[17]对非线性分数规划问题进行求解,提出最优的功率分配方案。为了方便后文分析,记为
| $ f\left(p^{\mathrm{mec}}\right)=\sum\limits_{i=1}^N p_i^{\mathrm{mec}} I_i, $ | (26) |
| $ \begin{aligned} g\left(p^{\mathrm{mec}}\right)=\sum\limits_{i=1}^N W^b \log _2\left(1+\frac{p_i^{\mathrm{mec}} h_i}{\sigma^2}\right)。\end{aligned} $ | (27) |
令F(pmec, μ)=f(pmec)-μg(pmec),其中μ为一个正的参数因子,pmec为总传输功率。基于优化问题P2.1a,形成一个新的优化问题:
| $ \begin{aligned} & \text { P2. } 1 \mathrm{a}^* \min _{p^{\mathrm{mec}}} F\left(p^{\mathrm{mec}}, \mu\right), \text { s. t. }~~~~ \mathrm{C} 3, \mathrm{C} 4, \mathrm{C} 6, \\ & \mathrm{C} 8 \text { 。} \end{aligned} $ | (28) |
根据Ghazi等[19]给定的定理,通过实现F(μ)=0,可以证明优化目标P2.1a可以等价于P2.1a*。f(pmec), g(pmec)是连续函数和实值函数,且g(pmec)通常大于0;pmec∈S,其中S是优化问题P2.1a和P2.1a*中参数pmec的定义域。下面给出使用Dinkelbach方法的具体过程。
基于Dinkelbach方法求解功率分配子问题的算法步骤如下。
步骤1:取p0mec∈S,计算μ1=minf(p0mec)/g(p0mec)和令i=0。
步骤2:决定
pimec=argminpimec∈S{min{f(pmec)-μig(pmec)}}。
步骤3:如果F(μi)=0,则pimec就是在值μi下问题(25)的最优解决方案,算法停止;否则转到步骤4。
步骤4:计算μi=minf(pimec)/g(pimec);计算i=i+1,转到步骤2。
上述算法的关键是在步骤2中获得功率分配pimec,因此问题可以转化为如何在给定μ下找到子问题P2.1a*的最优方案。运用障碍函数法[20]来解决上述问题,其中目标子问题可以转化为一系列不带约束的最小化问题。子问题P2.1a*的障碍函数为
| $ \begin{array}{r} \varphi\left(p^{\mathrm{mec}}\right)=-\sum\limits_{i=1}^N l b\left(R_i^{\mathrm{max}}-R_i^{\mathrm{mac}}\right)-l b\left(p_{\mathrm{max}}^{\mathrm{mec}}-\right. \\ \left.\sum\limits_{i=1}^N p_i^{\mathrm{mec}}\right)-\sum\limits_{i=1}^N l b\left(E_i^{\mathrm{eh}}-E_i^{\mathrm{mec}}\right)-\sum\limits_{i=1}^N l b\left(T_i^{\mathrm{max}}-T_i^{\mathrm{mec}}\right), \end{array} $ | (29) |
其中lb表示以2为底的对数。
子问题P2.1a*的最优解决方案能够通过解决如下非约束的最小值问题来估计:
| $ \min \Psi_v\left(p^{\mathrm{mec}}\right)=-v F\left(p^{\mathrm{mec}}, \mu\right)+\varphi\left(p^{\mathrm{mec}}\right), $ | (30) |
其中,v>0,决定近似值的准确程度。通过求解式(30)得到最优的pimec, *。
在D2D卸载模式下,λilocal=0, λimec=0, λi, jd2d=1,RUs的能耗最小化问题可以表示为
| $ \mathrm{P} 2.1 \mathrm{~b} \min\limits _{p_i^{\mathrm{d} d}} E_i^{\mathrm{d} 2 \mathrm{d}, t} \text {, s.t. } \quad \mathrm{C} 3, \mathrm{C} 5, \mathrm{C} 7, \mathrm{C} 8 。$ | (31) |
同样地,优化问题P2.1b可以用解决优化问题P2.1a的方法求解,最后得到pid2d, *。
2.3.2 求解任务卸载子问题根据上述求解功率分配子问题得到的pimec, *和pid2d, *,将原问题P1转化为一个仅与λilocal、λimec、λi, jd2d有关的子问题,即
| $\text { P2. } 2~~ \min \limits_{\lambda_i^{\text {local }}, \lambda_i^{\text {mec }}, \lambda_{i, j}^{\text {d2d }}} E^{\text {total }}, \text { s. t. }~~~~ \mathrm{C} 1, \mathrm{C} 2, \mathrm{C} 3, \mathrm{C} 6 \text {, }\\ \text { C8。} $ | (32) |
鉴于任务的不可拆分性,任务只能选择3种卸载模式中的1种。为了减少RUs的能耗,优先考虑卸载计算。注意这里一个服务用户只能与一个请求用户建立D2D通信链接进行卸载计算。式(32)中的优化问题就可以变成二部图中的一对一匹配问题,可以用匈牙利算法[21]求解。
为了解决问题P2.2,本文将优化问题P2.1(包含P2.1a和P2.1b两个子问题)映射为一个完全加权二部图G0=(V1, V2, E, W),V1和V2表示顶点集合,其中V1表示由还未确定卸载模式的剩余RUs组成的集合,V2表示由各种任务卸载模式组成的集合。E={e(v1, v2)}表示V1中的一个顶点v1到V2中的一个顶点v2之间边的集合,W={w(v1, v2)}表示边e(v1, v2)∈E的权重,即给定不同卸载模式下RUs能量消耗的最小值。
基于匈牙利算法求解任务卸载子问题的算法步骤如下。
步骤1:找到一个初始可行顶点标记为l(v1)。
步骤2:对于给定的l(v1),从G0中确定Gl0,并选择最大匹配H。
步骤3:如果H是最优匹配,则求解式(32)中的优化问题;否则,在Gl0中选择H未被分配的标签。令P=V1,T=ψ,ψ表示空集。
步骤4:NGl0(S)=T表示点集。如果NGl0(P)≠T,返回步骤3;否则计算
| $ l^{\prime}(v 1)=\left\{\begin{array}{c} l(v 1)-\Delta, v 1 \in P \\ l(v 1)+\Delta, v 1 \in T 。\\ l(v 2), \text { 其他 } \end{array}\right. $ | (33) |
步骤5:用l′(v1)替换l(v1),返回步骤2。
反复执行上述过程,可以得到最优的计算卸载策略,即λilocal,*, λimec,*, λi, jd2d,*。
能耗最小化任务卸载算法的具体过程描述如下:
算法1 能耗最小化任务卸载算法
输入:Wb,Wd,σ2
输出:λilocal,*, λimec,*, λi, jd2d,*,pimec, *,pid2d, *,Etotal, *
1.初始化:λilocal,*, λimec,*, λi, jd2d,*∈{0, 1},Rimax>0,pmaxmac>0,pmaxd2d>0;
2.if(λilocal=0&&λimec=1&&λi, jd2d=0)then
3. 将P1转化为P2.1a;
4. 根据Dinkelbach方法,将P2.1a转化为P2.1a*;
5. 然后根据障碍函数法求得RUi到MEC服务器的上行传输功率pimec, *;
6.else if(λilocal=0&&λimec=0&&λi, jd2d=1)then
7. 将P1转化为P2.1b;
8. 同样根据障碍函数法求得RUi到SUj的上行传输功率pid2d, *;
9.end if
10.将pimec, *,pid2d, *代入P1,得到P2.2;
11.根据匈牙利算法求得λilocal,*, λimec,*, λi, jd2d,*;
12.将λilocal,*, λimec,*, λi, jd2d,*代入式(23), 求得Etotal, *;
13.输出最优解(λilocal,*, λimec,*, λi, jd2d,*,pimec, *,pid2d, *)和最优目标解Etotal, *。
3 仿真实验与结果分析仿真实验在R2018b版本的MATLAB上实现。本文采用蒙特卡罗实验方法对所提策略进行性能评估,假设信道系数独立同分布,且服从瑞利分布。模拟区域的大小为200 m×200 m,假设移动用户均匀分布在模拟区域内。为方便实验对比分析,仿真实验参数设置[6]如下:最大数据传输速率Rmax=30 kbps,MEC最大上行功率pmaxmec=5 W,D2D最大上行功率pmaxd2d=1 W,基站到请求用户i的下行功率pieh=10 W,能量转换率β=0.7,功率分流比率ρ=0.5,能耗系数κ=10-28,完成RUi任务的计算资源量=5 Gigacycles,RUi的计算能力Fi=1 Gigacycles/s,MEC服务器的计算能力Fmec=30 Gigacycles/s,SUj的计算能力Fjd2d=1.2 Gigacycles/s,SUi输入数据大小Ii=1 Mbits,最大可容忍时延Tmax=0.1 s。
设置3个基准策略与本文所提策略进行对比实验,即本地执行、MEC卸载策略和D2D卸载策略(图中简称MEC卸载和D2D卸载)。MEC卸载策略表示任务执行仅依靠本地执行和MEC卸载模式执行;D2D卸载策略表示任务执行仅依靠本地执行和D2D卸载模式执行;而本文所提策略则是本地执行、MEC卸载、D2D卸载3种模式联合执行。分别给出不同的请求用户数量、噪声功率、BS的信道带宽等,观察本文策略以及3个基准策略RUs总能耗的变化情况,分析本文所提出的任务卸载策略的性能及有效性。
第一个实验是观察不同的请求用户数量N对RUs总能耗的影响,实验结果如图 4所示。在该仿真中,考虑服务用户数量M分别为4、6、8的情况。从图 4可以看出,随着RUs数量N的增多,所有卸载策略RUs的总能耗也随之增加。当N≤10时,本文提出的策略与MEC卸载策略中RUs的总能耗保持不变,且耗能很少,这是因为本文假设MEC服务器只能同一时刻执行10个移动用户的任务,当RUs不大于10时,这两个策略都是将任务卸载到MEC服务器上执行。当N>10时,本文策略由于可以将任务卸载到邻近的服务用户SUs执行,所以RUs的总能耗增长缓慢,且总能耗均低于其他2个基准策略。针对不同的SUs数量M,从本文策略与D2D卸载策略RUs的总能耗变化趋势来看,SUs的数量越多,RUs的总能耗越低,当RUs的数量高于SUs时,总能耗按照相同的斜率增长。总的来说,将任务全部卸载到MEC服务器的策略的执行优于全部进行D2D卸载的策略,而本文策略的性能优于MEC卸载策略和D2D卸载策略。

|
| 图 4 不同SUs数量M下RUs的数量N与RUs总能耗的关系 Fig. 4 Relationship between the quantity N of RUs and the total energy consumption of RUs under different SUs quantity M |
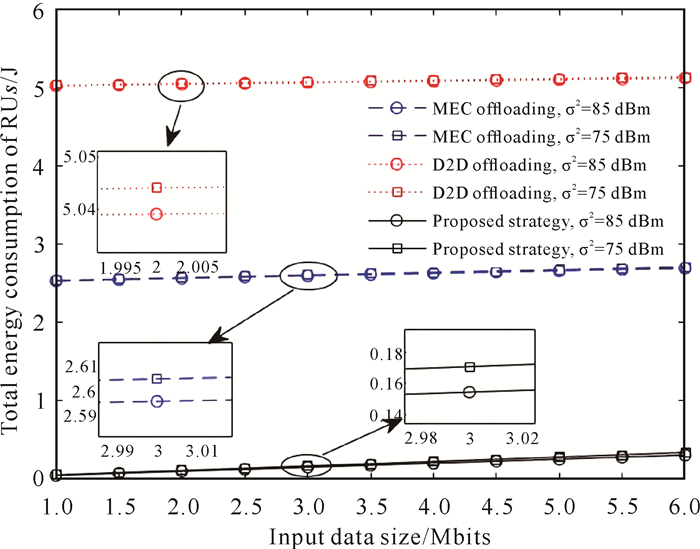
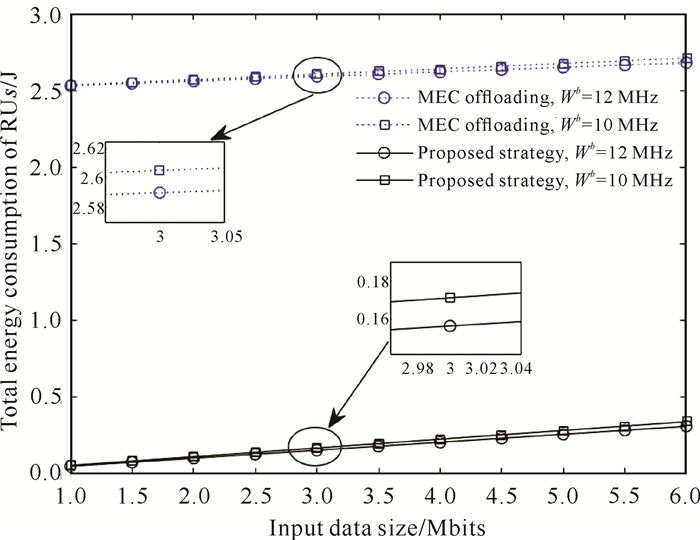
图 5和图 6分别给出了在不同的噪声功率σ2和基站信道带宽Wb下输入数据大小对RUs总能耗的影响结果。实验设置RUs=15,SUs=5,σ2设置-75 dBm和-85 dBm 2种情况。从图 5可以看出,RUs的总能耗随输入数据大小的增大而缓慢增长。在相同的输入数据大小下σ2越小,RUs的总能耗相对较小,这是因为噪声功率σ2会影响数据传输速率,σ2越小数据传输速率越大,数据传输速率直接影响传输能耗的大小。从图 6可以看出,针对不同的Wb,在相同的输入数据大小下BS的带宽Wb越大,RUs的总能耗越小,这是因为Wb与任务卸载到MEC服务器的数据传输速率Rimec呈正相关,当RUs传输任务到MEC服务器时,数据传输速率Rimec越大, RUs到MEC服务器的传输能耗越小。总的来说,Wb对请求用户总能耗有一定的影响,但是影响不大,随着输入数据量增大,Wb对请求用户总能耗的影响在小幅度增大。
|
| 图 5 不同σ2下输入数据大小与RUs总能耗的关系 Fig. 5 Relationship between input data size and the total of RUs under different σ2 |
|
| 图 6 不同Wb下输入数据大小与RUs总能耗的关系 Fig. 6 Relationship between input data size and the total energy consumption of RUs under different Wb |
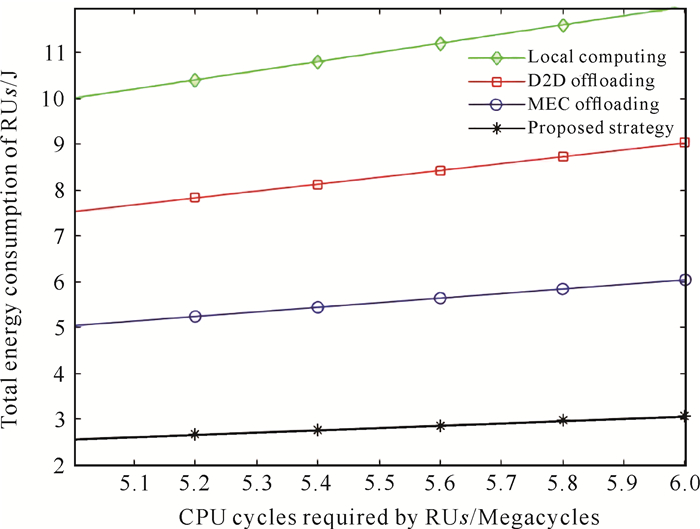
图 7给出了本地执行、MEC卸载、D2D卸载和本文所提策略等4种策略在不同RUs所需的CPU周期数下RUs的总能耗,该实验中设置RUs=20,SUs=5。从图 7可以看出,随着请求用户RUs的CPU周期数的增大,消耗的总能量也随之增大。本文所提策略的RUs总能耗明显低于其他3个基准策略,这表明本文所提策略能够较好地提高系统性能。这是因为本文所提策略优先选择MEC卸载,当MEC服务器中资源竞争加剧时,又考虑D2D卸载,可合理利用附近空闲的设备。从图 7还可以看出,MEC卸载和D2D卸载的RUs总能耗要低于本地执行的能量消耗,这得益于MEC服务器和服务用户的高效资源利用。MEC卸载策略比D2D卸载策略消耗的能量更加少,主要是MEC服务器为移动设备任务的执行提供更多可用的资源和能量,而D2D卸载虽然在一定程度上能够减少本地资源的使用,但是资源还是不如MEC服务器充足。
|
| 图 7 不同RUs所需的CPU周期数下的RUs总能耗 Fig. 7 Total energy consumption of RUs under different CPU cycles required by RUs |
图 8给出了在不同的D2D链路带宽Wd下随着BS的带宽Wb增大对RUs总能耗的影响结果。如图 8所示,随着Wb的增大,请求用户消耗的总能量随之降低;随着D2D链路带宽Wd的增大,请求用户消耗的总能量随之减小,是因为Wd与D2D数据传输速率Rd2d有关,且呈正比关系。当请求用户传输任务到服务用户时,数据传输速率越大,能量消耗越小。从实验结果来看,本文所提策略整体优于MEC卸载策略,这是由于本文所提策略比MEC卸载策略多了一种D2D卸载方式,请求用户可以考虑优先将任务卸载到邻近的空闲设备。

|
| 图 8 不同Wd下BS的带宽与RUs总能耗的关系 Fig. 8 Relationship between bandwidth of BS and total energy consumption of RUs under different Wd |
综合以上实验结果可知,针对由SWIPT技术供电后移动用户功率分配和任务卸载问题,本文所提策略是在MEC卸载策略的基础上联合D2D卸载策略,使得MEC资源争用问题得以解决,也避免了本地计算资源不足的问题,保证了移动用户的任务执行过程不会产生中断,避免对计算结果造成影响。因此,本文策略优于其他几种对比策略。
4 结论本文在保证通信服务质量的条件下,构建了一个基于SWIPT的多用户D2D通信辅助的MEC系统模型,并基于该模型分别建立能量收集和任务执行两个数学模型;考虑任务卸载和功率分配对目标函数和约束条件的影响,建立了一个非线性混合整数规划问题模型,提出了一种基于SWIPT的多用户D2D通信辅助MEC任务卸载策略。该策略以请求用户总能耗最小为目标,通过数学变化将原非线性混合整数规划问题转换为任务卸载和功率分配两个子问题:首先,利用Dinkelbach方法将目标函数转换为非分式规划问题,并用障碍函数法将目标子问题转化为一系列不带约束的最小化问题来求解功率分配子问题;然后,基于匈牙利算法将任务卸载子问题转化为二部图中的一对一匹配问题进行求解。仿真实验结果表明,在相同的SWIPT技术为移动设备供电的情况下,本文所提策略在最小化系统请求用户总能耗方面具有良好的性能。
| [1] |
谢人超, 廉晓飞, 贾庆民, 等. 移动边缘计算卸载技术综述[J]. 通信学报, 2018, 39(11): 138-155. |
| [2] |
YOU C, HUANG K. Multiuser resource allocation for mobile-edge computation offloading[C]//2016 IEEE Global Communications Conference (GLOBECOM). Washington DC, USA: IEEE, 2016: 1-6.
|
| [3] |
YOU C, HUANG K, CHAE H, et al. Energy-efficient resource allocation for mobile-edge computation offloading[J]. IEEE Transactions on Wireless Communications, 2017, 16(3): 1397-1411. DOI:10.1109/TWC.2016.2633522 |
| [4] |
ALI Z, JIAO L, BAKER T, et al. A deep learning approach for energy efficient computational offloading in mobile edge computing[J]. IEEE Access, 2019, 7: 149623-149633. DOI:10.1109/ACCESS.2019.2947053 |
| [5] |
薛建彬, 安亚宁. 基于边缘计算的新型任务卸载与资源分配策略[J]. 计算机工程与科学, 2020, 42(6): 959-965. DOI:10.3969/j.issn.1007-130X.2020.06.002 |
| [6] |
CHAI R, LIN J, CHEN M, et al. Task execution cost minimization-based joint computation offloading and resource allocation for cellular D2D MEC systems[J]. IEEE Systems Journal, 2019, 13(4): 4110-4121. DOI:10.1109/JSYST.2019.2921115 |
| [7] |
HE Y, REN J, YU G, et al. Joint computation offloading and resource allocation in D2D enabled MEC networks[C]//ICC 2019-2019 IEEE International Conference on Communications (ICC). Piscataway, NJ, USA: IEEE, 2019: 1-6.
|
| [8] |
KAI Y, WANG J, ZHU H. Energy minimization for D2D-assisted mobile edge computing networks[C]//ICC 2019-2019 IEEE International Conference on Communications (ICC). Piscataway, NJ, USA: IEEE, 2019: 1-6.
|
| [9] |
MAO Y, ZHANG J, LETAIEG K B. Dynamic computation offloading for mobile-edge computing with energy harvesting devices[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(12): 3590-3605. DOI:10.1109/JSAC.2016.2611964 |
| [10] |
SREELAKSHMY K R, JACOB L. Simultaneous wireless information and power transfer in heterogeneous cellular networks with underlay D2D communication[J]. Wireless Networks, 2020, 26(5): 3315-3330. DOI:10.1007/s11276-020-02261-y |
| [11] |
WEN Z, YANG K, LIU X, et al. Joint offloading and computing design in wireless powered mobile-edge computing systems with full-duplex relaying[J]. IEEE Access, 2018, 6: 72786-72795. DOI:10.1109/ACCESS.2018.2879334 |
| [12] |
CHEN F, FU J, WANG Z, et al. Joint communication and computation resource optimization in FD-MEC cellular networks[J]. IEEE Access, 2019, 7: 168444-168454. DOI:10.1109/ACCESS.2019.2954622 |
| [13] |
FU J, HUA J, WEN J, et al. Optimization of energy consumption in the MEC-assisted multi-user FD-SWIPT system[J]. IEEE Access, 2020, 8: 21345-21354. DOI:10.1109/ACCESS.2020.2969467 |
| [14] |
FU J, HUA J, WEN J, et al. Optimization of achievable rate in the multiuser satellite IoT system with SWIPT and MEC[J]. IEEE Transactions on Industrial Informatics, 2021, 17(3): 2072-2080. DOI:10.1109/TII.2020.2985157 |
| [15] |
马惠荣, 陈旭, 周知, 等. 绿色能源驱动的移动边缘计算动态任务卸载[J]. 计算机研究与发展, 2020, 57(9): 1823-1838. |
| [16] |
李陶深, 施安妮, 王哲, 等. 基于SWIPT的吞吐量最优化NOMA全双工中继选择策略[J]. 通信学报, 2021, 42(5): 87-97. |
| [17] |
ZHOU N, HU J, HOU J. Research on energy efficiency of NOMA-SWIPT cooperative relay network using GS-DinkelBach algorithm[J]. Sensors, 2021, 21(17): 5720. DOI:10.3390/s21175720 |
| [18] |
李陶深, 宁倩丽, 王哲. SWIPT-NOMA机会协作系统的优化方案[J]. 通信学报, 2020, 41(8): 141-154. |
| [19] |
GHAZI A, ROUBI A. Optimality conditions and DC-Dinkelbach-type algorithm for generalized fractional programs with ratios of difference of convex functions[J]. Optimization Letters, 2021, 15(7): 2351-2375. DOI:10.1007/s11590-020-01694-w |
| [20] |
SAMADI P, MOHSENIAN-RAD A H, SCHOBER R, et al. Optimal real-time pricing algorithm based on utility maximization for smart grid[C]//2010 First IEEE International Conference on Smart Grid Communications. Piscataway, NJ, USA: IEEE, 2010: 415-420.
|
| [21] |
KHAN A A, ADVE R S, YU W. Optimizing downlink resource allocation in multiuser MIMO networks via fractional programming and the hungarian algorithm[J]. IEEE Transactions on Wireless Communications, 2020, 19(8): 5162-5175. DOI:10.1109/TWC.2020.2990176 |



