2. 广西科学院,广西南宁 530007
2. Guangxi Academy of Sciences, Nanning, Guangxi, 530007, China
缆索承重桥梁是复杂地貌中公共交通的主要部分之一,具有跨径大、自重轻、节省材料的优点,常用在河道宽、水深、桥墩施工难度大的地方。缆索承重桥梁对交通建设以及经济发展具有重大意义,一旦发生桥梁事故将会对经济以及社会造成恶劣的影响。拉索是缆索承重桥梁结构承力的关键部分,拉索在服役期间会受到桥址环境和车辆荷载的影响:在经济发达的主城区,受道路交通长期拥挤及超载的影响,桥梁拉索易发生金属疲劳;而在南方沿海地区,由于长期处于高温、高湿的环境,拉索内部容易发生锈蚀断丝等病害,进而影响桥梁安全。因此,对拉索关键参数如索力、锈蚀度、断丝率等的检测和监测具有非常重要的意义。
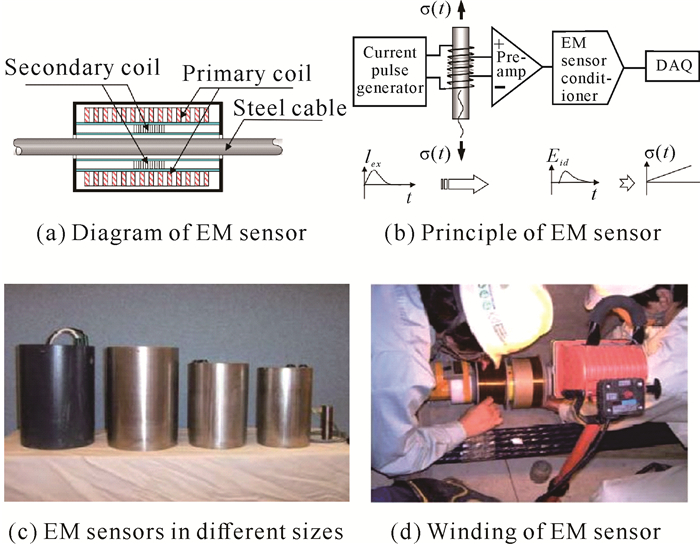
拉索索力状态是衡量桥梁是否处于正常运营状态的一个重要标志。国内外的研究机构对拉索索力测量方法进行了大量研究,如振动频率法[1]、应变元件法[2]、磁弹效应法[3, 4]等。磁弹效应法利用拉索内钢丝的铁磁性及其被磁化后,拉索磁导率受应力的变化而变化的这一规律,来实现拉索的索力测量。基于磁弹效应法的磁通量索力传感器(Elasto-Magnetic force sensor, EM sensor)因其具有高可靠性、长使用寿命、高测量精度和在线测量等优点,因而受到业界重视,并在工程上被广泛应用[5-7]。但该方法在理论及技术上仍存在突破空间,还需要对励磁结构的设计优化、励磁方式和工作参数的选择、温度补偿策略、长导线影响、传感器服役期的校准及快速安装方法、力-磁-温多场耦合效应等关键技术和机理进行深入研究,以提高传感器的测量精度、经济性、耐用性和适用性。因此,本文从磁通量索力传感器的工作原理出发,对近年来磁通量索力传感器的技术和应用进展进行综述,以期为新一代高精度的磁通量索力传感器技术的研究开发提供参考。
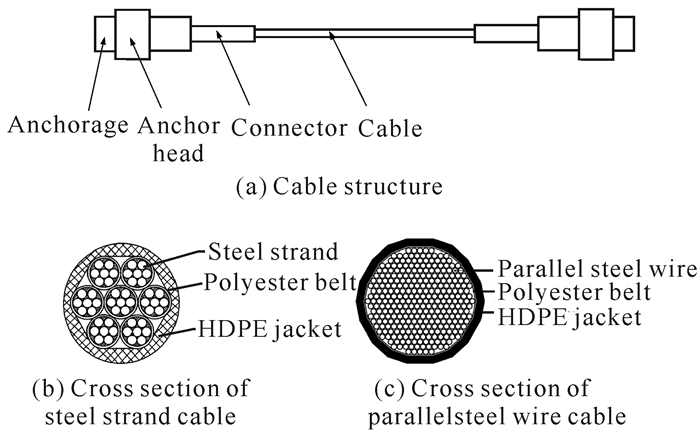
1 磁通量索力传感器的基本原理 1.1 拉索的磁特性与磁滞回线拉索的整体结构如图 1所示,包含锚头与索身两大部分。锚头主要由锚杯、锚圈和连接筒组成。而索身则由高强钢丝或钢绞线(铁磁材料)、聚酯纤维带、内层防腐材料和空气间隙、外层聚乙烯(Polyethylene,PE)防护套组成。而索身中的高强钢丝或钢绞线是拉索承力的部分,属于铁磁材料,决定了拉索的磁特性。
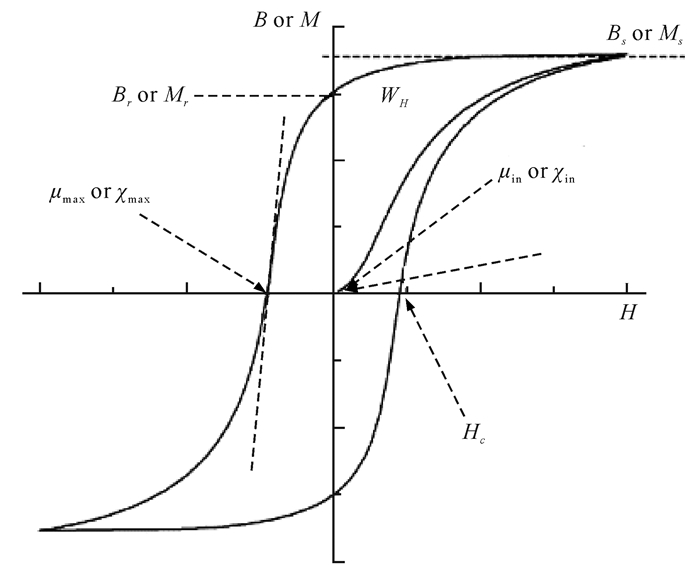
铁磁材料的磁性来源于材料内部的磁畴结构,即为了抵消外磁场的影响、降低退磁能,而形成小且具有一定取向的磁化区域[10]。当磁场存在时,铁磁材料内部的磁畴会在磁场的作用下发生转动或位移,以抵消外磁场、降低退磁能,同时显示外磁性。铁磁材料的磁性具有非线性与饱和性的特点。此外,还存在磁滞现象,即铁磁材料被磁化之后,磁感应强度B的变化滞后于磁场强度H,如图 2所示。由图 2可知,铁磁材料的初始磁化曲线和磁滞回线存在几个特殊点,即材料典型的磁特性参数,如饱和磁感应强度Bs、矫顽场Hc、剩余磁感应强度Br、初始磁导率μin和最大磁导率μmax。
|
| 图 2 铁磁材料的磁特性曲线 Fig. 2 Magnetic characteristic curve of ferromagnetic materials |
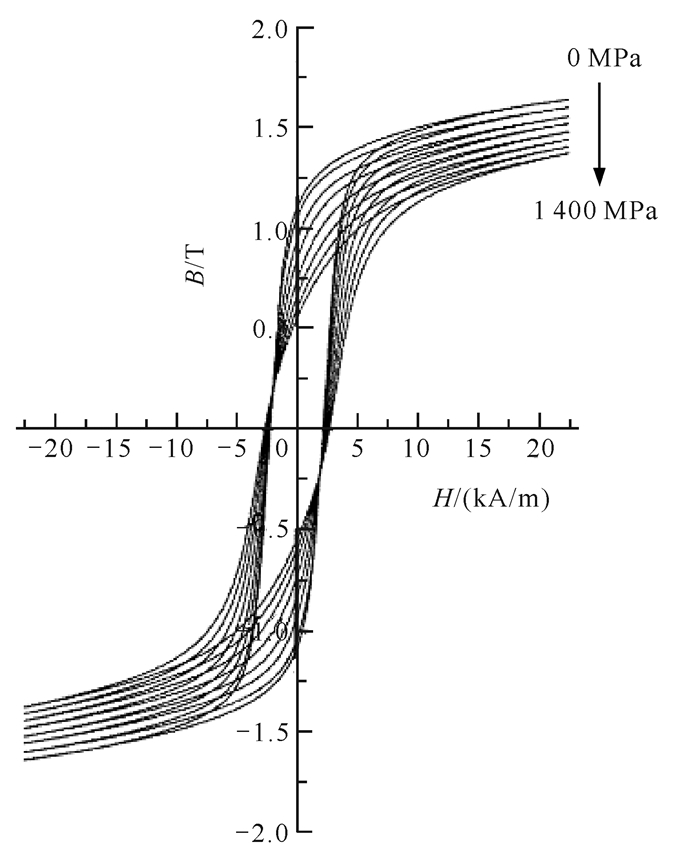
当铁磁材料受到张拉力时,铁磁材料内部的磁畴会拉伸和旋转,进而引起铁磁材料磁特性参数的变化。Kvasnica等[11]研究铁磁材料在不同应力荷载下的磁特性曲线,发现其磁特性曲线的变化与应力荷载存在显著相关性(图 3),为拉索索力监测奠定了实验基础。
在理论方面,Jiles等[12]为了从微观物理机理上描述磁滞模型,提出Jile-Atherton (J-A)模型,将磁化矢量M分为可逆部分Mrev与不可逆部分Mirr,建立铁磁材料的磁特性与内部磁畴的结构、分布及磁畴间相互作用强度的关联。在这基础上,Sablik等[13]提出J-A-S模型,定性解释了应力作用下磁滞回线斜率和形状的变化规律。
1.2 磁通量索力传感器的工作原理在铁磁材料所受应力与其磁特性参数相关性研究的基础上,科技工作者对获取铁磁材料磁特性参数的传感技术进一步展开了研究。磁通量索力传感器是其中一种获取拉索的磁导率传感器。根据图 2,可由磁感应强度B随磁场强度H的相对变化率,得出铁磁材料的磁导率μr的量化表达式为
| $ \mu_r=\frac{1}{\mu_0} \frac{\Delta B}{\Delta H} 。$ | (1) |
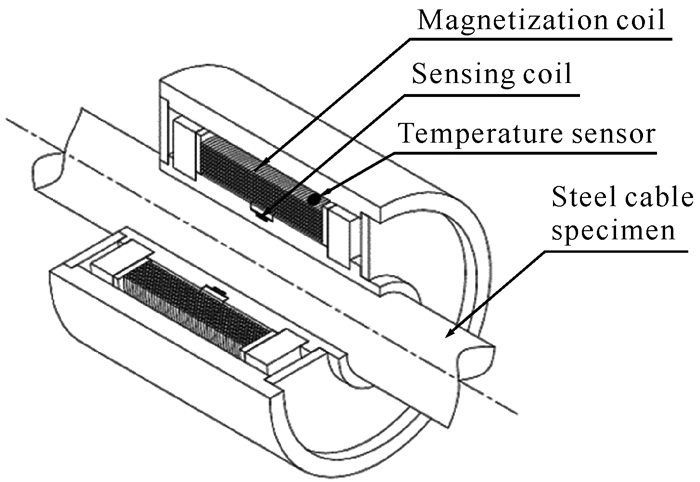
因此,如果给拉索施加变化磁场ΔH,并同步测量其磁感应强度的变化量ΔB,则可由式(1)求出磁导率μr,再根据传感器的标定关系式求出拉索的拉力。为实现上述功能,设计磁通量索力传感器的基本结构如图 4所示[14],其主要由给拉索施加磁场H的励磁线圈、获取拉索磁感应强度B的感应线圈、温度传感器及传感器的支撑与防护结构组成。其中,励磁线圈和感应线圈为螺线管结构,与拉索同轴,传感器整体呈套筒式结构套在拉索上。
励磁线圈通入激励电流后,产生激励磁场,对被测拉索进行磁化。当激励电流变化时,被测拉索内的磁通量亦改变,根据法拉第感应定律,此时感应线圈两端产生的感应电压Vind(t)大小[6]为
| $ \;\;\;\; V_{\text {ind }}(t)=-N\left[A_f \frac{\mathrm{d} B_t}{\mathrm{d} t}+\left(A_0-\right.\right. \\ \left.\left.A_f\right) \mu_0 \frac{\mathrm{d} H(t)}{\mathrm{d} t}\right], $ | (2) |
式中,N为感应线圈的匝数,μ0为真空磁导率,A0和Af分别为感应线圈与拉索的横截面。
若对上式在[t1, t2]时间范围内的感应电压Vind进行积分,则可得感应线圈输出的积分电压Vout为
| $ \;\;\;\; \;\;\;\; V_{\text {out }}=\int_{t_1}^{t_2} V_{\text {ind }}(t) \mathrm{d} t=-N A_f\left[\Delta B+\left(\frac{A_0}{A_f}-\right.\right. \\ \text { 1) } \left.\mu_0 \Delta H\right], $ | (3) |
显然,感应电压的幅值Vind与拉索的磁感应强度变化量ΔB呈线性关系。
如果线圈中未放置被测拉索,则式(3)所示的感应线圈输出的积分电压V0可简化为如下:
| $ V_0(t)=N A_0 \mu_0 \Delta H, $ | (4) |
将两式相除,可得:
| $ \frac{V_{\text {out }}}{V_0}=\frac{1}{\mu_0} \frac{A_f}{A_0} \frac{\Delta B}{\Delta H}+\left(1-\frac{A_f}{A_0}\right), $ | (5) |
因此,相对磁导率μr可用感应线圈的输出幅值V、感应线圈横截面A0与拉索横截面Af来表示:
| $ \mu_r=1+\frac{A_0}{A_f}\left(1-\frac{V_{\text {out }}}{V_0}\right) 。$ | (6) |
若μF与μin分别是有应力与无应力时测量得到的相对磁导率,并定义有应力与无应力下的相对磁导率之差为增量磁导率Δμ,即
| $ \Delta \mu=\mu_F-\mu_{\text {in }}, $ | (7) |
显然增量磁导率Δμ与拉索索力F(即构件的应力)存在直接关联。具体而言,两者之间存在以下多项式函数关系[15]:
| $ F=C_3 \Delta \mu^3+C_2 \Delta \mu^2+C_1 \Delta \mu+C_0+\delta(\Delta \mu), $ | (8) |
其中,δ(Δμ)为高次项误差。因此,若忽略高次项误差δ(Δμ),并通过静载标定试验确定系数C0、C1、C2、C3后,即可利用式(8)实现对拉索索力F的测量。由于线性项系数C1占主要贡献,则在一定条件下,式(8)还可进一步简化为以下线性关系:
| $ F \approx C_1 \Delta \mu+C_0 。$ | (9) |
拉索的磁化特性与理论是研究磁通量索力传感器的重要理论基础。要测量拉索的磁导率,首先对其进行磁化,而其磁化的程度主要由铁磁材料的磁性与所处的磁场环境共同决定。在1.1节中已经对铁磁材料的非线性、磁滞效应和磁饱和特性等研究进展进行了综述,本节主要探讨在磁通量索力传感器工作时,拉索所处区域磁场的来源及其对拉索磁化的影响。
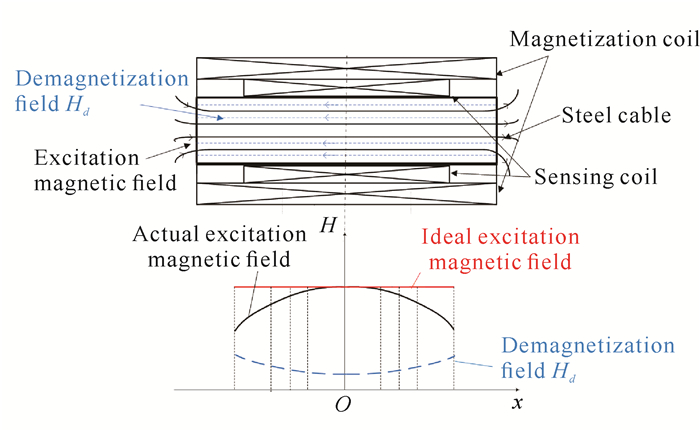
磁化磁场为外源性磁场与内源性磁场的叠加。外源性磁场主要来源于磁通量索力传感器的励磁线圈工作时产生的磁场。磁通量索力传感器内部的励磁线圈为螺线管结构。理想螺线管在通电后,其内部分布高均匀的磁场。但理想螺线管线圈难以实现,因此实际的励磁线圈是有限长度的螺线管结构,其内部磁场具有不均匀性,轴向磁场强度在螺线管中间处最高,往两边逐渐降低,如图 5所示。
从图 5还可以看出,拉索被磁化后会产生退磁场Hd,一般采用退磁因子γ这一参数来描述退磁场与磁场强度的关系[10]:
| $ H_d=\gamma H 。$ | (10) |
被测拉索的退磁因子γ与其自身的材质、几何形状相关。昝会萍等[17]将拉索近似看作理想圆柱形结构,研究了圆柱形磁介质在均匀磁场中的退磁场和退磁因子,给出了有限圆柱体内任意一点的退磁场与退磁因子的表达式,并指出圆柱体轴线上两端的轴向退磁因子较大,中间的轴向退磁因子较小。退磁场的存在使拉索所处的磁场不均匀性变得更加复杂,因此,根据退磁场的分布规律来优化感应线圈的位置与长度,可优化传感器的灵敏度与可重复性[18]。
此外,地磁场与传感器周围铁磁性结构件的磁场亦会对拉索所处区域的磁场有贡献,但地磁场强度(0.045 Tesla)对拉索磁化效果相较于励磁线圈(约1 Tesla)而言较小。因此在对传统结构磁通量索力传感器的研究上一般忽略地磁场的影响。
内源性磁场主要来源于铁磁材料本身的磁滞效应。如1.1节所述,磁滞效应主要来源于磁畴在转动与旋转过程中不可逆过程的贡献。磁场与应力的施加与撤去的过程,都有可能产生磁滞。磁通量索力传感器的理想工作状态为测得的磁特性参数与受到的应力数值具有单一的确定关系。但磁滞效应的存在使得拉索在相同的磁场下磁特性参数亦可能不同,即拉索的磁化历史将影响拉索的力-磁耦合关系,导致力-磁耦合关系出现与磁化历史相关的多样性和非线性[19]。
为了消除磁滞带来的滞回误差,需要对拉索磁化历史进行稳定控制,以提高磁通量索力传感器的准确性。磁场强度变化引起的磁滞效应一般通过对拉索反复磁化,使其剩余饱和磁场强度达到最大值,从而减少这部分磁滞效应的影响[20]。对于应力加载与卸载引起的磁滞效应这一方面,刘琳[19]对应力相关的滞回误差效应及相应的抑制方法开展了研究,通过控制激励磁场的施加方式,降低滞回误差的影响。
3 磁通量索力传感器的结构 3.1 套筒式传感器结构用于桥梁拉索监测的磁通量索力传感器最基本的结构是套筒式磁通量索力传感器,最早由Jarosevic[21]、Kvasnica等[11]在20世纪90年代末提出。2000年Wang等[3]推动了这一结构的传感器的应用与技术发展。套筒式磁通量索力传感器的基本结构如图 6所示,该传感器安装在拉索索体上,通过多层螺线管励磁线圈与测量线圈对拉索进行激励与磁信号测量。这类传感器与拉索同轴,因此该类型传感器的偏心效应影响小。同时,该类型的传感器适配性好,可以根据拉索的直径制造不同的尺寸,能用于直径在12-250 mm的拉索上。此外,其不仅适用于新建拉索,对于已服役的拉索还可通过现场绕制的方式安装。
但随着拉索直径的增大,励磁线圈的直径及所需励磁电流迅速增大,实现理想螺线管线圈结构的经济代价急剧增加,拉索的磁化效果与测量精度急剧下降。因此,要想保证传感器的准确性,需要对励磁部分等进行优化设计,形成均匀、稳定的磁场,以获得较好的磁弹效应,同时优化传感器的体积、用料,使其经济合理。
张茹[20]研究对比了不同线圈的长度与直径的比值(长径比)下的励磁线圈内部磁场分布,发现当单层励磁线圈的长径比大于5时,励磁线圈可近似理想的螺线管线圈,内部磁场具有高均匀度;而对于多层励磁线圈,在相同的匝数下,励磁线圈层数越多,长径比越小,均匀磁场的范围也越小,这些结果为励磁线圈的设计提供了理论参考。
在励磁线圈为有限螺线管线圈构型的框架内,科技工作者对励磁线圈的几何构型与绕制方案开展了研究,以优化绕线长度与匝数,并通过有限元仿真建模进行验证。例如,广西科学院对磁通量索力传感器的励磁线圈开展了有限元建模仿真研究[14],分析了励磁线圈在不同几何参数和线圈参数下的励磁能力,设计了可对圆钢吊杆的索力进行测量的磁通量索力传感器,并开展实验验证设计传感器的有效性。李登峰等[22]、秦志勇等[23]等亦对传感器的励磁线圈的设计及仿真开展了研究。
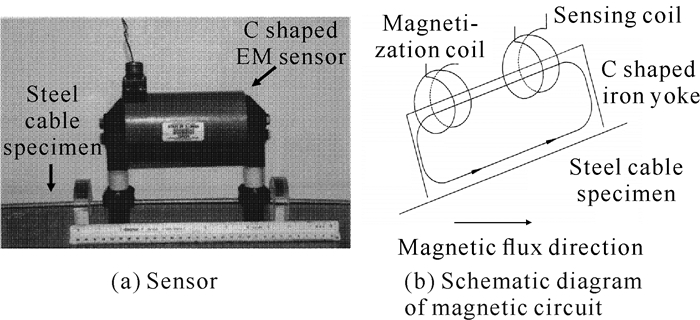
3.2 非套筒式传感器结构由于大跨度缆索承重桥梁一般具有上百根拉索,如果拉索全部安装磁通量索力传感器,则经济花费较大;而且对于在役的拉索而言,套筒式磁通量索力传感器还存在现场安装、拆卸与重安装的难题。因此,非套筒式磁通量索力传感器应运而生。Jarosevic[21]在1996年提出U型结构的磁通量索力传感器。2001年,Wang等[24]提出C型结构的磁通量索力传感器(图 7)。轭铁与被测构件形成磁回路,励磁线圈与感应线圈被绕制在旁路的轭铁处,其传感器的固定主要靠轭铁与拉索之间的固定件连接,因而具有拆装方便、便携性好的优点。但由于其结构与图 4所示的套筒式结构不同,其磁路有很大差异,导致磁特性参数的测量结果与套筒式传感器的测量结果存在较大偏差。
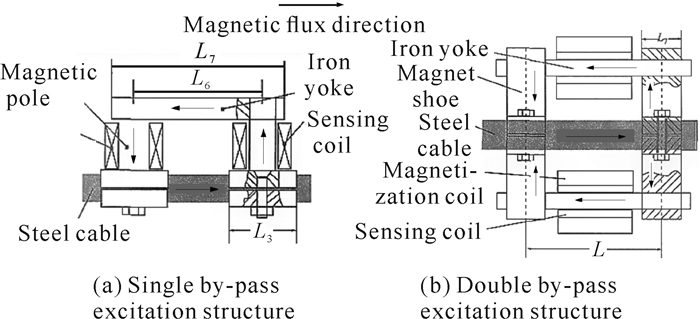
唐德东[25]在2006年最早开展了单旁路非套筒式结构传感器的研究,其设计的单旁路励磁结构类似于C型线圈,区别在于励磁线圈与测量线圈分别位于磁回路的两个磁靴上,以降低线圈之间的互感。除此之外,该团队还研究了双旁路的励磁结构,利用两个旁路的励磁线圈对拉索进行磁激励,以减少励磁所需的电流大小。旁路励磁式磁通量索力传感器结构如图 8所示。小直径拉索的拉力实验结果表明,单旁路励磁结构的磁通量索力传感器测量的重复性误差小于0.15%,满足小直径拉索索力测量的实际需求。但当拉索承受的拉力较大或者钢丝直径较大时,双旁路励磁结构对力-磁规律及构件的磁化效果急剧恶化,需进一步优化传感器结构和工作参数以提升实用性。黄捷[26]也对类似结构的外装式磁通量索力传感器开展研究。
虽然非套筒式结构具有拆装方便、便携性的优点,但是其线圈的非对称结构使得拉索的磁化不均匀,导致磁特性参数的测量结果与理想套筒式结构的测量结果存在差异。因此目前旁路式磁通量索力传感器主要是应用在小直径(< 20 mm)的拉索索力检测。针对上述问题,可借鉴其他领域科技工作者的研究成果作进一步优化,如谈兵等[27]提出一种旁路的二级励磁磁路结构,可实现对直径40 mm的大直径钢丝绳的轴向均匀励磁。
4 传感器的性能提升研究 4.1 励磁技术为了能获得稳定的磁特性参数,使之能与应力之间建立明确的对应关系,不仅需要对励磁线圈的结构进行设计优化,还需要优化激励电流的施加方式、强度等参数。
对于线圈中的被测拉索而言,其作用类似于线圈中的铁芯,因此励磁线圈的电感L不可忽略。如激励源采用电容放电的工作方式,此时励磁线圈与激励源等共同构成的放电回路模型是一个RLC串联二阶电路,其电路中电压uc相应的二阶微分方程如式(10)所示[28]:
| $ L C \frac{\mathrm{d}^2 u_c}{\mathrm{~d} t^2}+R C \frac{\mathrm{d} u_c}{\mathrm{~d} t}+u_c=0, $ | (10) |
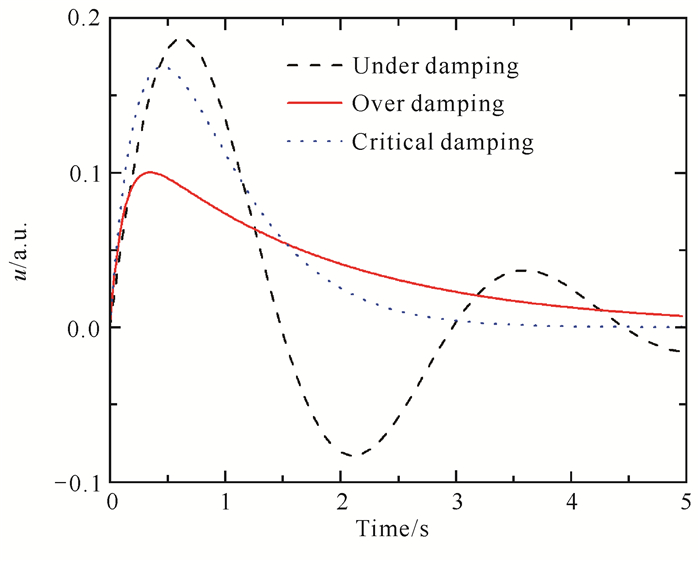
根据电阻R与电感L、电容C的关系,放电电路存在3种解,分别为欠阻尼(
|
| 图 9 RLC串联电路不同的放电状态 Fig. 9 Different discharge states of RLC series circuit |
励磁电流的施加方式有直流励磁、交流励磁、脉冲励磁或多种励磁方式组合。励磁方式的选择与拉索的磁特性参数相关。虽然增量磁导率是磁通量索力传感器实现对拉索索力测量的主要参数,但是铁磁材料的其他磁特性参数与索力的依赖性也受到广泛关注。Makar等[29]通过交流励磁的方式,研究了矫顽场Hc、剩余磁感应强度Br、饱和磁感应强度Bs与张拉力F的关系。结果发现,当张拉力处于较低范围时,矫顽场Hc不变或与张拉力F呈负相关;而当张拉力处于较大范围时,Hc与张拉力F呈正相关;剩余磁感应强度Br随张拉力F的变化呈相反趋势,即在索力较低范围时与张拉力F呈正相关,在索力较高范围时与张拉力F呈负相关;而饱和磁感应强度Bs则是随着张拉力F的增加而下降。这些实验结果表明,多种磁特性参数亦与应力存在相关性,但该相关性的适用性、稳定性和唯一性仍需要进一步研究。
除励磁技术外,磁通量索力传感器的励磁工作点的选取也关系到测量的准确性。唐德东[25]根据铁磁材料的非线性磁性特点将磁通量索力传感器的工作点选择在磁导率最高的区域,以提高感应信号的幅值。刘琳[19]则将磁通量索力传感器的工作点选择在初始磁化曲线上,以减小滞回误差对索力测量准确性的影响,并采用差动式传感结构,消除外磁场的干扰,使稳定性误差小于1%、滞回误差小于3%、测量误差小于5%。Wang等[5]则将工作点选择在铁磁材料的近饱和区,此时磁滞循环面积小,材料的磁感应强度几乎不受磁化历史的影响,从而保证测量的精准度。综上所述,科技工作者对磁通量索力传感器中关于励磁工作点的选择的研究内容丰富,但在实际工程上主要选择在拉索磁特性曲线的近饱和区。
4.2 灵敏度提升传统的磁通量索力传感器采用法拉第感应线圈实现对铁磁材料磁信号的测量,而感应线圈测磁法是历史最悠久、应用最广泛的磁场测量方法。该方法的测磁灵敏度与频率相关,信号频率越高,测量越灵敏。但磁通量索力传感器有效信号主要位于频域上的低频部分[30],表明磁通量索力传感器的感应线圈未在其最优的工作区域中。
为了提高微分磁导率的测量灵敏度,科技工作者也尝试用其他磁场测量技术来代替感应线圈。Zhang等[31]利用磁敏传感器作为磁通量索力传感器的磁场探测单元,基于磁电层合材料,由高磁致伸缩系数Terfenol-D合金和强压电系数的PZT压电陶瓷层合形成,其磁场-电压转换系数达186.5 mV/Oe,该方法获得的磁信号幅值比感应线圈法获得的信号幅值大10倍,有效提高了磁通量索力传感器对磁信号的探测效率。这种类型的磁通量传感器亦被称为电磁弹索力传感器[32-34]。
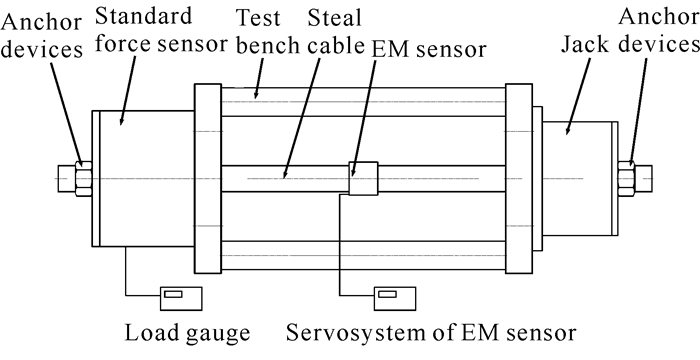
5 磁通量索力传感器的性能标定研究 5.1 实验室标定实验磁通量索力传感器作为一个计量装置,出厂前需要进行标定,即对传感器的微分磁导率与拉索张力、温度等因素的关系进行实验标定。由于拉索需要承受数百甚至上千吨的拉力,因而高精度、大吨位的标定实验平台是关键,一般由张拉台座、张拉千斤顶、标准力传感器及与实际拉索同型号的拉索样件等组成,张拉台座上安装有拉索样件、锚具等,其原理如图 10所示[14]。由图 10可知:磁通量索力传感器安装在拉索样件上;磁弹仪输出励磁电流至磁通量索力传感器的感应线圈并接收磁通量索力传感器的信号;标准力传感器串接安装在张拉千斤顶上,在千斤顶张拉过程中同步记录标准力传感器与磁通量索力传感器的输出,并将不同荷载下的测量结果对式(8)中各系数进行拟合,完成工作曲线的标定;之后,根据工作曲线多次测量的结果,统计磁通量索力传感器的重复性及精确度。
该类实验台不仅可用于传感器标定,还能开展铁磁材料磁导率与索力之间关系的基础研究。Wang等[5]利用标定实验台研究微分磁导率与索力之间的关系,发现在0-1 000 MPa的千斤顶油泵变化范围内,微分磁导率与索力存在显著的线性相关性。Cappello等[15]利用标定实验台在更广泛的应变力范围内开展研究,发现增量磁导率与索力的关系不是严格的线性关系,当负载大于4 000 kN时,采用三次多项式拟合更合适,但仍是线性关系占主导。Wang等[3]利用标定实验台不仅标定了多种不同钢丝材料的磁导率-拉应力关系,还对多股钢线的磁导率-拉应力关系进行测量与研究,发现多股钢线中每股的磁导率-拉应力关系平均结果与整个拉索整体测量得到的磁导率-拉应力结果几乎相等。Yim等[35]利用标定实验台研究了不同材质与直径的拉索的磁导率-索力关系,发现同种材质不同直径拉索的工作曲线的斜率几乎相同。Zonta等[36]进一步研究发现,同一型号的不同传感器标定曲线斜率相同、截距存在差异,说明磁通量索力传感器的一致性好,但仍需对其进行标定。
5.2 应用现场标定实验虽然传感器经过实验室标定后,能够确保其出厂时的测量准确性,但是作为一个计量装置,在实际现场的长期应用中,还面临现场校准的难题,特别是对于现场绕制而成的磁通量索力传感器。
现场标定的技术主要分两类。一类是千斤顶法,即对在役钢缆安装千斤顶进行张拉,并对千斤顶的拉力、拉索上在役的磁通量索力传感器进行标定。Zhao等[6]对比了在实验室通过张拉法与在施工现场通过千斤顶法对同一传感器标定的结果,发现两种工况下同一传感器的工作曲线的斜率几乎相同,在标定的32个传感器中,这两种方法标定的传感器的测量结果最大误差均不超过2%。另一类常用的现场标定方法为对比法,即将磁通量索力传感器的数据与其他索力传感器的结果进行对比。最常用的对比手段是通过加速度传感器获得拉索的振动基频,再通过拉索振动模型计算得到当前拉索的索力值,从而间接地对磁通量索力传感器的工作参数进行标定。Zonta等[36]研究了基于振频法的磁通量索力传感器现场校准技术,经过校准后,磁通量索力传感器可用于索力测量,测量准确度为200 kN,主要受限于振频法结果的精度与温度的影响。Liu等[37]利用频率法对磁通量索力传感器标定开展研究,通过建立频率法中各阶固有频率与磁通量索力传感器输出信号的关系模型,降低拉索振动模型和结构参数的选取对传感器标定结果的影响,实现对磁通量索力传感器的标定。
6 磁通量索力传感器的温度影响由于磁性材料的磁特性是力场、磁场、温度场等多场耦合的综合影响。当温度升高时,铁磁材料磁畴内的电子运动剧烈,铁磁材料的磁导率降低,外显磁性减弱,由于传感器输出受环境温度的影响,因此传感器温度效应的影响是磁通量索力传感器标定的研究热点之一。Kvasnica等[11]研究了温度对铁磁材料磁弹效应的影响,认为温度对铁磁材料特征参数的贡献与拉应力的贡献相当,表明在磁通量索力传感器的实际应用中,需要矫正温度效应的影响。因此必须在磁通量索力传感器内部再增加一个温度传感器,以获取温度信息,进而补偿温度效应的影响。
温度对磁通量索力传感器的影响,还与传感器磁场的测量方式、工作点以及积分范围的选取相关。Wang等[3]研究了不同工作点下温度效应对测量结果的影响,虽然选取的3个工作点下温度对磁导率的影响都是线性的,且线性范围较广(-20-40 ℃),但是不同工作点下的磁导率与温度的线性关系的斜率有所区别。对于采用磁电层合材料的磁传感器,由于传感器本身输出信号亦受温度的影响,测量得到的磁导率与温度的关系为非线性,更适合用多项式拟合[38]。
磁通量索力传感器的温度效应标定实验一般也在张力台座上进行,首先将一个可控制温度的恒温箱包裹住磁通量索力传感器及部分拉索,然后将恒温箱设置一定的温度,待恒温箱内温度达到平衡后,测量该温度下磁通量索力传感器的输出。此外,秦志勇[39]采取另外一种温度实验标定平台方案,将整个张拉设备装入恒温箱内,以降低拉索局部加热可能导致误差的影响。对磁通量索力传感器进行微分磁导率与拉索张拉力的标定以及磁导率与温度的标定后,即可用于索力的监测。
7 磁通量索力传感器的应用及发展趋势 7.1 磁通量索力传感器的工程应用磁通量索力传感器由于线圈的寿命长且不直接承受拉力,因而具有高可靠、长寿命的优点,受到工程界的广泛重视,国内外皆推出了商业产品,如美国的IIS公司、捷克的INSET公司等;而国内的柳州欧维姆机械股份有限公司[7]已有成熟产品在国内土木工程领域广泛应用。
国内外的高校、科研机构、企业等更是将磁通量索力传感器广泛应用于各种大跨度缆索承重桥梁,如重庆大学陈伟民团队、浙江大学段元锋团队、同济大学张其林团队、广西科学院王晓琳团队等也对磁通量索力传感器样机应用于各类预应力拉索结构进行了研制。表 1列出了部分磁通量索力传感器的应用实例及效果。
| 序号 No. |
被测构件直径/mm Diameter of the tested component/mm |
准确度 Accuracy |
备注 Note |
参考文献 Reference |
| 1 | 12 | 0.286% F.S. | Parallel steel strand, laboratory | [40] |
| 2 | 15.24 | 1% F.S. | Steel strand with PE package, Yinbin Yangtze River Bridge | [41] |
| 3 | 20 | 2% F.S. | Parallel steel strand, Ganjiang River Bridge | [42] |
| 4 | 80 | Maximum error 2% | Galfan cables, one Suspension Bridge in Fujian Province | [33] |
| 5 | 85 | >2% F.S. | Round steel suspender, laboratory | [14] |
| 6 | 116/128 | ≈2% F.S. | Steel strand cable, Adige Bridge in Italy | [13] |
| 7 | 116/119/140 | Maximum error 8.4% | Steel cable, Zhengzhou Olympic Sports Center | [43] |
| 8 | 120 | 1.6%-2.45% F.S. | Steel strand cable, Jiaojiang Second Bridge | [20] |
| 9 | 127 | Accuracy<3% | Parallel steel strand cable, Liuzhou Wenhui Bridge | [44] |
| 10 | 160 | Accuracy>2% | Steel strand cable, Stonecutters Bridge | [6] |
| 11 | 200 | Accuracy 2% | Steel strand cable, Hwa-Myung Bridge in South Korea | [35] |
| Note: F.S.indicates full scale error. | ||||
从实际工程应用效果来看,小直径拉索的测量精确度可优于2%,而大直径拉索的测量精度为2%-8%。限制磁通量索力传感器在大直径拉索上测量精度的主要因素在于励磁源的性能和稳定性以及励磁线圈的线圈参数、均匀性能否对被测构件充分磁化。此外,磁通量索力传感器还可应用于电梯[45],矿井[46]、大型体育场馆[47]、高边坡预应力加固[48]、大型科学装置[49]等领域。
7.2 传感器应用的关键技术 7.2.1 长导线效应及克服技术磁通量索力传感器在实际应用中会比实验室环境面临的难题更多。拉索桥梁一般是大跨度桥梁,传感器探头与信号处理端需靠长达数十或数百米的信号线连接,这部分信号线可能会额外给测量系统带来电阻值的变化,进而影响测量结果的准确性,因此需要解决信号传输线长度影响的问题。Zhou等[50]研究了不同传输线距离下磁通量索力传感器对测量结果的影响,发现当传输线的长度从50 m增加到200 m时,磁通量索力传感器的综合测量误差从-2.3%增加到-4.94%。Ren等[43]提出一种比值测量方法,采用感应电压积分值与激励电流变化的比值来代替感应电压积分值对索力进行表征,以降低电阻变化对测量结果的影响,该方案能将传感器的相对灵敏度提高11%。
7.2.2 新型数据处理方法与技术在其他领域应用广泛的数据处理方法或智能化信息处理技术,也被应用到磁通量索力传感器的性能升级与技术研究中。比如谐波和频谱处理技术[31, 51]、机器学习[52]、神经网络[38]等,用于磁特性参数的测量和温度补偿,以提高磁通量索力传感器的准确度、可靠性与鲁棒性等。此外,传感器在实际桥梁的索力检测过程中会产生大量的数据,借助数字孪生技术对大量数据进行处理分析,将有益于拉索寿命建模与对其服役状态的分析。
7.3 磁通量索力传感器的发展趋势 7.3.1 磁通量索力传感器性能提升的深入研究目前磁通量索力传感器技术还面临机理与技术的难题,仍需要进一步对其开展研究。比如,磁通量索力传感器采样频率不高,约为0.1 Hz量级[6], 不能实现高频测量,限制其在高动态索力监测的场景使用;铁磁材料具有磁致伸缩的特性,铁磁材料的磁化过程与磁畴间的相互运动有关,反复磁化是否会加速拉索的金属疲劳或影响其材料的力学性能,这个问题有待进一步研究,进而延长拉索的服役时间;便携性磁通量索力传感器的结构与工作原理如何进一步优化,以提高拆装便携性与精度是值得关注的问题。另外,由于磁通量索力传感器的成本较高,用户往往只在一座桥上选取有限的几根拉索进行监测,如果能进一步降低传感器系统的成本,就有可能突破大规模应用的瓶颈,全面应用于桥梁的所有拉索上。此外,对传感器服役期在线校准技术仍需要进一步深入研究,全面解决其服役期校准的技术、设备和工艺,实现其长期测量准确性,也是促进磁通量索力传感器应用的关键。
7.3.2 基于磁法的无损检测磁通量索力传感器的另外一个发展方向是扩展其在无损检测领域中的应用。如前所述,磁通量索力传感器不仅能获得磁导率的信号,还可以获得矫顽场、饱和磁感应强度等磁特性参数,而这些磁特性参数也可以反映铁磁材料的健康状态。封小亮等[53]研究发现,铁磁材料本身的矫顽场强度与其金属疲劳等级存在关联性,随着金属疲劳等级增加,矫顽场的测量数值亦增大;刘秀成[54]和徐江等[55]采用新技术如磁致伸缩导波法检测基于铁磁材料固有的磁致伸缩效应及其逆效应,可实现对拉索断丝与锈蚀的缺陷检测。磁通量传感法与磁致伸缩导波法的传感器都存在励磁部件与励磁测量部件,实现这两种方法的有机耦合是相关领域的前沿问题。因此,需要对磁场的精确调控技术、高精度大量程电源技术、主被动励磁技术等共性技术展开进一步研究,以更好地将磁通量索力传感器与其他磁学方法结合,实现多维拉索参数的检测,这将是磁通量索力传感器未来的发展方向之一,为铁磁材料的无损检测提供更全面的方法。
8 展望磁通量索力传感器作为一种非接触式测量的索力传感器,具有服役寿命长、精度高等优点。自面世以来,一直受到无损检测及结构健康监测领域的科技工作者的广泛关注。目前科技工作者对磁通量索力传感器的工作原理、结构优化、磁化过程、温度效应、灵敏度提升、标定方法、工程应用等方面进行了全面研究,使得传感器在桥梁索力、高边坡加固、大跨度体育场馆的结构健康监测等多个领域广泛应用。
随着预应力体系在各类大型土木结构中的使用增加,磁通量索力传感器的应用领域也将更为广阔。同时也能促使科技工作者对线圈的自动化绕线技术、防腐技术、阵列式传感器技术、混凝土密封技术等开展更全面与深入的研究,进一步提高传感器的模块化、智能化和可靠性,使其能更好地用于保障公共安全。
| [1] |
任伟新, 陈刚. 由基频计算拉索索力的实用公式[J]. 土木工程学报, 2005, 38(11): 26-31. DOI:10.3321/j.issn:1000-131X.2005.11.005 |
| [2] |
李冬生, 周智, 欧进萍. 光纤光栅智能复合筋传感特性及其工程应用[J]. 光电子·激光, 2009, 20(10): 1294-1297. DOI:10.3321/j.issn:1005-0086.2009.10.006 |
| [3] |
WANG M L, CHEN Z L, KOONTZ S S, et al. Magnetoelastic permeability measurement for stress monitoring in steel tendons and cables[C]//Nondestructive Evaluation of Highways, Utilities, and Pipelines Ⅳ. Newport Beach, CA: SPIE, 2000: 492-500.
|
| [4] |
郝超, 裴岷山, 强士中. 斜拉桥索力测试新方法: 磁通量法[J]. 公路, 2000, 11: 30-31. |
| [5] |
WANG G D, WANG M L, ZHAO Y, et al. Application of EM stress sensors in large steel cables[C]//Smart Structures and Materials. Belingham, WA: SPIE, 2005: 395-406.
|
| [6] |
ZHAO Y, WANG M L. Fast EM stress sensors for large steel cables[C]//Nondestructive Characterization for Composite Materials, Aerospace Engineering, Civil Infrastructure, and Homeland Security. San Diego, CA: SPIE, 2008: 209-216.
|
| [7] |
邓年春, 龙跃, 孙利民, 等. 磁通量传感器及其在桥梁工程中的应用[C]//中国土木工程学会桥梁及结构工程分会, 天津市建设管理委员会. 第十八届全国桥梁学术会议论文集(下册). 北京: 人民交通出版社, 2008: 643-648.
|
| [8] |
中华人民共和国交通运输部. 挤压锚固钢绞线拉索: JT/T 850-2013[S]. 北京: 人民交通出版社, 2013.
|
| [9] |
国家市场监督管理总局, 中国国家标准化管理委员会. 斜拉桥用热挤聚乙烯高强钢丝拉索: GB/T 18365-2018[S]. 北京: 中国标准出版社, 2018.
|
| [10] |
姜寿亭, 李卫. 凝聚态磁性物理[M]. 北京: 科学出版社, 2003.
|
| [11] |
KVASNICA B, FABO P. Highly precise non-contact instrumentation for magnetic measurement of mechanical stress in low-carbon steel wires[J]. Measurement Science and Technology, 1996, 7(5): 763-767. DOI:10.1088/0957-0233/7/5/007 |
| [12] |
JILES D C, ATHERTON D L. Theory of ferromagnetic hysteresis[J]. Journal of Magnetism and Magnetic Materials, 1986, 61(1/2): 48-60. |
| [13] |
SABLIK M J, KWUN H, BURKHARDT G L, et al. Model for the effect of tensile and compressive stress on ferromagnetic hysteresis[J]. Journal of Applied Physics, 1987, 61(8): 3799-3801. DOI:10.1063/1.338650 |
| [14] |
王晓琳, 朱茂华, 章鹏, 等. 拱桥圆钢吊杆拉力监测的磁弹传感技术研究[J]. 仪器仪表学报, 2022, 43(9): 140-148. |
| [15] |
CAPPELLO C, ZONTA D, LAASRI H A, et al. Calibration of elasto-magnetic sensors on in-service cable-stayed bridges for stress monitoring[J]. Sensors, 2018, 18(2): 466. DOI:10.3390/s18020466 |
| [16] |
刘小亮. 磁弹索力传感器设计方法及实验研究[D]. 重庆: 重庆大学, 2011.
|
| [17] |
昝会萍, 许启明, 张引科. 轴向均匀磁化圆柱形磁介质的退磁场和退磁因子[J]. 西安建筑科技大学学报(自然科学版), 2009, 41(3): 409-412. DOI:10.3969/j.issn.1006-7930.2009.03.020 |
| [18] |
刘小亮, 陈伟民, 章鹏, 等. 传感器内部磁场分布对磁弹索力传感器性能的影响[J]. 仪器仪表学报, 2012, 33(4): 857-862. DOI:10.3969/j.issn.0254-3087.2012.04.021 |
| [19] |
刘琳. 杆索钢构件磁性法拉伸应力监测的力磁耦合机理与影响因素研究[D]. 重庆: 重庆大学, 2013.
|
| [20] |
张茹. 基于磁弹效应和磁电层合材料的在役钢结构应力监测研究[D]. 杭州: 浙江大学, 2014.
|
| [21] |
JAROSEVIC A. Magnetoelastic method of stress measurement in steel[J]. Nato ASI Series 3 High Technology, 1999, 65: 107-114. |
| [22] |
李登峰, 王刚, 杨可标. 磁弹式索力检测系统设计与仿真[J]. 传感器与微系统, 2017, 36(9): 67-69, 76. |
| [23] |
秦志勇, 邓年春. 最优磁化模型的磁通量传感器仿真实验与应用[J]. 石家庄铁道大学学报(自然科学版), 2022, 35(1): 70-75. |
| [24] |
WANG M L, LLOYD G M, HOVORKA O. Development of a remote coil magnetoelastic stress sensor for steel cables[C]//Health Monitoring and Management of Civil Infrastructure Systems. Newport Beach, USA: SPIE, 2001: 122-128.
|
| [25] |
唐德东. 基于磁弹效应的钢缆索索力在线监测关键技术探索[D]. 重庆: 重庆大学, 2007.
|
| [26] |
黄捷. 外装式高压励磁索力传感器设计与系统开发[D]. 南京: 东南大学, 2015.
|
| [27] |
谈兵, 杜润生, 康宜华, 等. 大直径钢丝绳轴向励磁磁路的研究[J]. 华中理工大学学报, 1994, 22(7): 36-39. |
| [28] |
胡翔骏. 电路分析[M]. 3版. 北京: 高等教育出版社, 2016.
|
| [29] |
MAKAR J, TANNER B. The in-situ measurement of the effect of plastic deformation on the magnetic properties of steel[J]. Journal of Magnetism and Magnetic Materials, 1998, 184(2): 193-208. |
| [30] |
LIU X C, WU D H, HE C H, et al. Comparison of AC and pulsed magnetization-based elasto-magnetic methods for tensile force measurement in steel strand[J]. Measurement, 2018, 117: 410-418. |
| [31] |
ZHANG R, DUAN Y F, OR S W, et al. Smart elasto-magneto-electric (EME) sensors for stress monitoring of steel cables: design theory and experimental validation[J]. Sensors, 2014, 14(8): 13644-13660. |
| [32] |
胡孝阳, 段元锋, 魏巍, 等. 高钒索索力监测电磁弹传感器的研发与应用[J]. 结构工程师, 2021, 37(2): 78-83. |
| [33] |
段元锋, 胡孝阳, 段元昌, 等. 基于磁弹效应的电磁弹式钢索(束)应力监测系统[J]. 中国科技论文在线精品论文, 2019, 12(5): 761-768. |
| [34] |
DUAN Y F, ZHANG R, DONG C Z, et al. Development of elasto-magneto-electric (EME) sensor for in-service cable force monitoring[J]. International Journal of Structural Stability and Dynamics, 2016, 16(4): 1640016. |
| [35] |
YIM J, SHIN S W, EEM S H, et al. Field application of elasto-magnetic stress sensors for monitoring of cable tension force in cable-stayed bridges[J]. Smart Structures and Systems, 2013, 12(3/4): 465-482. |
| [36] |
ZONTA D, ESPOSITO P, MOLIGNONI M, et al. Calibration of elasto-magnetic sensors for bridge-stay cable monitoring[C]//Proceedings of the Sixth European Workshop on Structural Health Monitoring. Dresden, Germany: [s. n. ], 2012: 164-171.
|
| [37] |
LIU X, CHEN Y, HU H, et al. Measurement method of natural frequencies and tension forces for cables based on elasto-magnetic sensors calibrated by frequencies[J]. AIP Advances, 2022, 12(1): 015301. |
| [38] |
ZHANG R, DUAN Y F, ZHAO Y, et al. Temperature compensation of elasto-magneto-electric (EME) sensors in cable force monitoring using BP neural network[J]. Sensors, 2018, 18(7): 2176. |
| [39] |
秦志勇. 基于磁弹效应的单旁路索力传感器理论分析与试验研究[D]. 南宁: 广西大学, 2022.
|
| [40] |
陈伟民, 姜建山, 章鹏, 等. 钢缆索索力磁性传感理论模型与实验研究[J]. 仪器仪表学报, 2010, 31(4): 794-799. |
| [41] |
何利, 邓年春. 磁通量传感器在宜宾长江大桥斜拉索监测中的应用[J]. 公路交通技术, 2010(1): 95-97. |
| [42] |
黄晔, 吴琛. 磁通量传感器在体外索力检测中的应用[J]. 建材技术与应用, 2007(10): 18-20. |
| [43] |
REN L, XIU C, LI H, et al. Development of elastomagnetic (EM) sensor for monitoring cable tension using an innovative ratio measurement method[J]. Smart Materials and Structures, 2018, 27(11): 115003. |
| [44] |
覃新育. 磁通量传感器在柳州文惠桥吊索监测中的应用[J]. 煤炭技术, 2008(4): 131-133. |
| [45] |
尤光辉. 电梯曳引钢丝绳力学性能及磨损研究[D]. 杭州: 浙江工业大学, 2014.
|
| [46] |
赵志科. 矿井提升钢丝绳的动态检测与故障诊断方法研究[D]. 徐州: 中国矿业大学, 2018.
|
| [47] |
陈鲁, 宋杰, 张其林. EM法测量索张力的理论与工程实践研究[J]. 施工技术, 2008(5): 144-148, 153. |
| [48] |
王晓琳, 周痒天. 磁通量传感器在高边坡预应力锚索索力监测中的应用[J]. 江西建材, 2015(18): 212-213. |
| [49] |
王晓琳, 李东平, 朱明, 等. FAST主动反射面健康监测系统设计与应用研究[J]. 广西科技大学学报, 2018, 29(4): 84-91, 98. |
| [50] |
ZHOU Y S, ZHANG J N, LIU C, et al. Performance analysis of by-pass excitation cable force sensor[J]. IOP Conference Series: Materials Science and Engineering, 2019, 647(1): 012017. |
| [51] |
FENG H, LIU X C, WU B, et al. Temperature-insensitive cable tension monitoring during the construction of a cable-stayed bridge with a custom-developed pulse elasto-magnetic instrument[J]. Structural Health Monitoring, 2019, 18(5/6): 1982-1994. |
| [52] |
KIM J, PARK S. Field applicability of a machine learning-based tensile force estimation for pre-stressed concrete bridges using an embedded elasto-magnetic sensor[J]. Structural Health Monitoring, 2020, 19(1): 281-292. |
| [53] |
封小亮, 马括, 刘课秀. 基于矫顽力的T91钢老化评价方法[J]. 理化检验-物理分册, 2022, 58(6): 26-28, 49. |
| [54] |
刘秀成. 磁致伸缩与磁弹一体化传感技术及其钢索检测应用研究[D]. 北京: 北京工业大学, 2013.
|
| [55] |
徐江, 汤欢, 武新军. 桥梁缆索断丝导波无损检测系统研制[J]. 无损探伤, 2010, 34(3): 19-21. |