2. 华南师范大学数据科学与工程学院, 广东汕尾 516600
2. School of Data Science and Engineering, South China Normal University, Shanwei, Guangdong, 516600, China
科学研究与工程实践中存在大量需要同时优化多个目标函数的问题,即多目标优化问题(Multi-objective Optimization Problem,MOP)。MOP各目标之间一般是相互冲突的,因此其一般不存在唯一的解,而往往是一组均衡各目标的折中解,即Pareto最优解集。进化算法(Evolutionary Algorithm, EA)是一类元启发式算法,运行一次可产生一组解,而且对待求解问题的数学性质不做特别假设,因而被广泛用于求解各类MOP,并由此产生了许多各具特点的多目标进化算法(Multi-Objective Evolutionary Algorithm,MOEA),如基于Pareto支配、基于指标和基于分解的MOEA等[1]。这些算法在求解决策变量数目不多的MOP时具有较好的性能,获得了令人鼓舞的结果。
近年来,一些要求优化含有更多决策变量的MOP不断涌现,如大规模公共交通网络设计问题[2]、大规模投资组合优化问题[3]、大规模资源分配问题[4]等。研究者习惯将决策变量数目超过100的MOP称为大规模多目标优化问题(Large-Scale Multi-objective Optimization Problem,LSMOP),以区别于决策变量数目不多的MOP。LSMOP的出现给传统的MOEA带来了严峻挑战,其主要原因在于:随着决策变量数目的线性增加,搜索空间的体积和复杂性将呈指数级增大,导致“维数灾难”问题,使得常规MOEA的优化性能在求解LSMOP时快速下降[5]。因此,恰当处理大规模决策变量是求解LSMOP的关键。
迄今,研究者针对大规模决策变量提出了一些对变量进行分组的方法,其目的是通过变量分组将LSMOP分解成若干含决策变量规模较小的子MOP。典型的分组方法包括随机分组[6]、差分分组[7]和变量分析[8, 9]等。随机分组利用“分而治之”的策略将大规模决策变量随机地分成相同规模的组(Group),然后轮流优化各变量组。该方法将一个LSMOP转化成若干小规模的MOP,然后运用一些经典的MOEA求解。随机分组方法的优点是简单有效且易于实现;不足之处在于未考虑变量间的交互,如果交互变量被分至不同组,算法将很难搜索到全局最优解。差分分组通过检测将交互变量划分至同组,然后轮流优化各组。这类方法的优点在于无需预先设置分组的规模,而且由于交互变量是在同组优化,这将有利于找到全局最优解。但这种方法需要检测变量交互,要耗费较多的计算资源,使得真正用于问题解优化的计算资源相对不足。变量分析通过分析决策变量对LSMOP目标函数的贡献(即收敛性和多样性影响)对变量进行分组,然后根据不同类型的分组采用不同的优化策略以获得收敛性和多样性俱佳的解集。如MOEA/DVA[8]通过控制变量分析将决策变量分成位置变量、距离变量和混合变量,实验结果表明,MOEA/DVA在一些LSMOP上表现出较好的性能,但不足之处在于需要开销大量计算资源用于评估目标函数,而且该算法也不能较好地处理含混合变量较多的LSMOP。针对MOEA/DVA的不足,LMEA[9]采用聚类方法将LSMOP的决策变量分成收敛性相关组和多样性相关组,并运用不同的方法分别优化,实验结果表明,该算法有利于改善解群的收敛性和多样性,但是LMEA的变量分解过程过于复杂且分组的效果不稳定。总体上,已有的大规模多目标进化算法(Large-Scale Multi-Objective Evolutionary Algorithm, LSMOEA)所使用的分组方法可在一定程度上降低求解LSMOP的难度并改善算法的性能,但它们仍有较大改进的空间。例如:大部分分组方法需要逐一检测决策变量的交互,需要开销大量的计算资源,使得真正用于优化问题解的计算资源相对不足;另外,一些算法还存在效率不高、解集质量不佳等问题。基于此,本文提出一种采用变量两阶段分组的多目标进化算法(Large-Scale Multi-Objective Evolutionary Algorithm Adopting Two-Stage Variable Grouping,LSMOEA/2s)。与已有的LSMOEAs所不同的是:一方面,LSMOEA/2s在分组过程中并未考虑变量对目标函数的贡献(如收敛性和多样性影响),而是根据变量间的相关性(或独立性)对变量实施分组,使得算法结构更简单;另一方面,算法采用基于变量组的相关性检测和随机分组方法实现对大规模变量快速分组,以期改善算法的性能。
1 背景知识定义1:不失一般性,以最小化问题为例,一个具有d个决策变量和m个目标的MOP可形式化定义如下:
| $ \min \boldsymbol{f}(\boldsymbol{x})=\left(\boldsymbol{f}_1(\boldsymbol{x}), \boldsymbol{f}_2(\boldsymbol{x}), \cdots, \boldsymbol{f}_m(\boldsymbol{x})\right), $ | (1) |
式中,x =(x1, x2, …, xd)表示决策空间Ω中任意解点x是d维的决策向量,f(x)表示包含了m个相互冲突且需最小化目标函数的目标向量。特别地,如果式(1)中的决策变量数目d大于或等于100,则式(1)中的问题又被称为LSMOP。正如式(1)所示,这里定义的LSMOP默认是不带任何约束条件的。
定义2: (Pareto支配)对于任何两个解x和y,x支配y(记为f(x)
定义3: (非支配)对于任何两个解x和y,x如果与y是非支配关系,当且仅当x不支配y且y不支配x。
定义4: (Pareto最优解)x是Pareto最优解当且仅当决策空间Ω中不存在任何其他的解y,使得y支配x。
定义5: (Pareto最优解集)LSMOP的所有Pareto最优解构成Pareto最优解集(Pareto optimal Set, PS)。
定义6: (Pareto最优前沿)LSMOP是所有Pareto最优解在目标空间的投影构成了Pareto最优前沿(Pareto optimal Front, PF)。
在大规模函数优化中经常需要对大规模决策变量进行分组,其中分组过程涉及函数的可分性问题。下面给出可分离函数的定义。
定义7: (可分离函数)f(x)是可分离函数当且仅当x中各决策变量xi(i=1, …, d)均可独立地优化,即
成立。否则,f(x)称为不可分离函数。
相应地,如果f(x)中部分决策变量不能独立地优化,则其被称为部分可分离函数。极端情况下,如果f(x)所有决策变量均不能独立地优化,亦即只能整体地优化,则f(x) 被称为完全不可分函数。
相关系数是用以反映变量之间相关关系密切程度的统计指标,通过计算决策变量间相关关系的概念对大规模决策变量进行简单分组,以下给出相关系数的定义。
定义8: (相关系数)设r表示相关系数,用以反映变量x和y之间的线性关系,其计算方式如下:
| $ r(x, y)=\frac{{Cov}(x, y)}{\sqrt{{Var}[x] {Var}[y]}}, $ | (2) |
式中,Cov(x, y)为变量x和y的协方差,Var[x]和Var[y]分别为变量x和y的方差。
此外,由于相关系数与相关强度之间并没有标准的分界点,对相关系数的解释是依赖于具体的应用背景和目的。根据Hemphill等[10]的研究,相关系数r的绝对值在0.8以上,一般认为变量间具有强相关性;r的绝对值为0.3-0.8,认为变量间有弱相关性;r在0.3以下,则认为变量间无相关性。
2 LSMOEA/2s目前LSMOEA所采用的分组方法一般需要逐一检测决策变量之间的交互性,该过程需要开销大量的计算资源,从而使得算法用于优化问题解的计算资源相对不足。另外,已有的一些LSMOEA还存在效率不高、求解质量较差等问题。本研究提出的LSMOEA/2s,其总体思路是首先利用基于变量组的相关性检测方法快速识别出独立变量,然后对非独立变量实施高频次的随机分组,最后利用MOEA/D优化各变量子组。LSMOEA/2s的主要创新点在于:① 根据变量间相关性(或独立性)对变量实施分组,算法的结构更简单;②采用基于变量组的相关性检测和随机分组方法对大规模变量进行分组,节省了大量计算资源用于优化问题的解。算法1给出了LSMOEA/2s的流程:第1步初始化各独立变量子组集和非独立变量集为空;第2步运用基于变量组相关性检测方法识别独立变量和非独立变量;第3至11步进行双重循环,其中算法的第4步利用随机分组方法对非独立变量进行分组;第5步构建变量子组的集合;第6至10步为内层循环,其功能是利用MOEA/D[11]对各变量子组逐一优化;第12步输出最终获得的种群。
算法 1:LSMOEA/2s的流程
输入:种群规模N,大规模决策变量数目d,基于变量组的相关性检测方法的采样个体数目为k,随机分组中分组的规模为R,最大评价次数为FEmax。
输出:最终种群pop。
1.初始化:FE=0,IV=Ø,NIV=Ø;pop={x1, x2, …, xN}//FE为函数评价计算器,IV为各独立变量子组集,NIV为非独立变量集。
2.[IV, NIV] ← group_based(pop, d, k); //运用基于变量组的相关性检测方法识别独立变量和非独立变量。
3.WHILE (FE < FEmax)
4. [NI_groups] ←random_group (NIV, R); //利用随机分组方法非独立变量进行分组。
5. all_groups ←[IV, NI_groups]; //构建变量子组的集合。
6. FOR i =1 TO size(all_groups)
7. FOR j =1 TO N
8. pop ← MOEA/D(pop, all_groups(i)); //使用MOEA/D算法[11]间优化。
9. END FOR
10. END FOR
11.END WHILE
12.输出最终种群pop。
需要指出的是,LSMOEA/2s的核心技术包括: ①运用基于变量组的相关性检测方法识别独立变量和非独立变量(步骤2所示);②随机分组方法对非独立变量进行分组(步骤4所示);③基于变量组的相关性检测方法group_based。算法2给出了group_based算法的流程。
算法 2:group_based算法
输入:种群规模N,当前进化种群pop,决策变量的数目d,采样个体数目k。
输出:独立变量组成的集合IV,非独立变量集合NIV。
1.初始化:IV=Ø,NIV=Ø;
2.FOR i=1 TO d
3. 随机从种群pop中选择k个个体,且X={xi1, xi2, …, xik}, Y={y1, …, yi-1, yi+1, …, yd}; //xik表示第k个个体的第i维变量,yi表示除第i个变量外的所有d-1个变量的均值。
4. 根据式(2)计算X和Y间的相关系数ri;
5. 利用ri进行显著性检验,计算p-值: pi;
6. IF (pi < 0.05 && |ri| >0.3)
7. NIV=NIV∪{xi};
8. ELSE IV=IV∪{xi};
9. END IF
10.END FOR
11.输出IV和NIV。
其中,在算法2的第2至第9步利用相关系数判别变量之间的线性相关性。第6步采取p < 0.05且|rij|>0.3为准则判别变量的独立性和非独立性。另外,算法2通过计算当前变量与剩余变量均值之间的相关性可快速判断出独立变量,独立变量各自成组,减少了不必要的适应度评价次数。
总体上,LSMOEA/2s经过第1阶段的变量分组获得了独立变量和非独立变量集合,但现实中LSMOP的高度复杂性使得非独立变量集合可能仍是大规模的。因此有必要对非独立变量集合进一步分组以降低优化问题的求解难度。这里采用高频次的随机分组方法对其进行分组,而且高频次随机分组有利于将具有交互性的变量分至相同的子组,从而有利于算法搜索全局最优解。
3 实验与结果分析 3.1 实验方案设计为检验LSMOEA/2s的性能,选取当前大规模多目标进化优化领域中具有代表性的算法MOEA/D、CCGDE3[12]、RVEA[13]和S3-CMAES[14],在3-目标LSMOP1-LSMOP9系列测试问题[15]上进行对比实验,各测试函数决策变量数目(D)分别取100、200、300和500维,共计在36个测试实例上进行实验,以获得较可靠的对比结果。其中100、200、300维的测试实例最大适应度评价次数设为500 000,500维的测试实例设为700 000。需要指出的是,实验选取LSMOP系列测试函数主要在于:LSMOP系列测试集是专门为LSMOP设计的系列测试函数,它们能刻画现实LSMOP可能存在的一些难度特征,如变量分组不均、变量与不同目标函数具有不同的相关性,特别是其位置变量与距离变量之间存在链接等。这些困难特征对LSMOEA构成了巨大挑战,因而能很好地检验算法的性能。
为检验算法的综合性能,这里利用反转世代距离(Inverted Generational Distance,IGD)指标评估算法获得解集的收敛性和多样性。具体地,IGD指标度量了真实的Pareto前沿到所获近似Pareto前沿之间的距离。由于实验中采用的LSMOP系列测试集的真实Pareto前沿是已知的,通过在真实Pareto前沿上均匀采集多样性的点,计算这些采样点到近似Pareto前沿解点之间的距离,则既能反映解集的收敛性,又能反映其多样性。一般而言,IGD值越小,表明近似Pareto前沿的收敛性和多样性越好。假设P是MOP真实Pareto前沿解集,IGD性能指标可利用公式(3)进行计算。
| $ \mathrm{IGD}=\frac{1}{|P|} \sum\limits_{i=1}^{|P|} { Dist }_i, $ | (3) |
其中,
为减少随机因素对性能评估的影响,实验中各算法在每一个测试实例中均独立执行30次(每次使用不同的随机数种子),以获得性能指标IGD的均值和方差。另外,实验利用显著水平为0.05的Wilcoxon秩和检验来分析各算法获得近似解集的性能在统计意义上的差异。符号+、-和=分别表示对比算法的IGD值明显优于、劣于和无差别于LSMOEA/2s。
本研究所有实验均在ASUS FL5600L PC上执行,PC配置如下:CPU为AMD A10-8700P、1.8 GHz主频、8.0 G内存、Windows 7 X64位操作系统,所有算法均在PlatEMO[16]平台上实现。
3.2 实验结果与分析表 1列出了LSMOEA/2s与其他4种算法在3-目标的LSMOP系列测试问题上获得的IGD均值和方差,表中各行的最好结果用粗体突显。
| 问题 Problem |
维度(D)
Dimensions (D) |
MOEA/D | CCGDE3 | RVEA | S3-CMA-ES | LSMOEA/2s |
| LSMOP1 | 100 | 1.3296e-1 (2.33e-2)= |
5.1038e+0 (1.01e+0)- |
2.0164e-1 (1.68e-2)- |
1.9632e-1 (6.33e-2)- |
1.5367e-1 (3.66e-2) |
| 200 | 1.4274e-1 (2.14e-2)= |
7.2281e+0 (9.14e-1)- |
3.4963e-1 (7.81e-2)- |
3.0631e-1 (7.40e-2)- |
1.5260e-1 (2.39e-2) |
|
| 300 | 1.6918e-1 (2.16e-2)= |
7.6786e+0 (8.51e-1)- |
5.8944e-1 (1.21e-1)- |
7.7988e-1 (1.17e-1)- |
1.7637e-1 (2.63e-2) |
|
| 500 | 1.8927e-1 (1.89e-2)- |
8.3002e+0 (9.48e-1)- |
7.3602e-1 (1.54e-1)- |
1.9905e+0 (4.23e-1)- |
1.7039e-1 (2.19e-2) |
|
| LSMOP2 | 100 | 1.2843e-1 (5.75e-3)- |
2.2402e-1 (6.13e-3)- |
1.0105e-1 (7.22e-3)= |
7.8601e-2 (2.12e-2)+ |
9.4787e-2 (1.43e-2) |
| 200 | 1.0132e-1 (1.93e-3)- |
1.3679e-1 (2.64e-3)- |
8.2602e-2 (2.04e-3)+ |
6.2475e-2 (7.60e-3)+ |
9.6372e-2 (1.76e-3) |
|
| 300 | 8.3154e-2 (1.05e-3)- |
1.0717e-1 (4.28e-3)- |
7.3697e-2 (1.31e-3)+ |
5.7927e-2 (4.43e-3)+ |
8.0097e-2 (9.54e-4) |
|
| 500 | 6.4132e-2 (3.77e-4)- |
8.0444e-2 (3.10e-3)- |
6.1143e-2 (6.32e-4)+ |
5.0722e-2 (1.31e-3)+ |
6.3240e-2 (4.74e-4) |
|
| LSMOP3 | 100 | 5.6754e-1 (1.42e-1)= |
1.3412e+1 (2.27e+0)- |
1.9563e+0 (1.01e+0)- |
1.8816e+0 (3.42e-1)- |
5.5817e-1 (1.48e-1) |
| 200 | 5.7464e-1 (1.68e-1)= |
1.6034e+1 (1.86e+0)- |
1.5854e+0 (5.01e-1)- |
5.6581e+0 (3.34e-1)- |
5.8545e-1 (1.73e-1) |
|
| 300 | 5.3264e-1 (1.55e-1)= |
1.7011e+1 (1.69e+0)- |
2.1260e+0 (8.56e-1)- |
7.7925e+0 (3.98e-1)- |
5.6927e-1 (1.01e-1) |
|
| 500 | 5.7162e-1 (1.51e-1)+ |
1.7684e+1 (1.79e+0)- |
2.6150e+0 (1.07e+0)- |
1.0362e+1 (5.27e-1)- |
6.3377e-1 (1.43e-1) |
|
| LSMOP4 | 100 | 2.2190e-1 (2.43e-2)= |
5.5810e-1 (1.48e-2)- |
2.7568e-1 (4.91e-2)- |
3.4614e-1 (3.26e-2)- |
2.0586e-1 (5.98e-2) |
| 200 | 2.5476e-1 (7.60e-3)- |
3.8685e-1 (1.28e-2)- |
1.9408e-1 (1.33e-2)= |
2.7150e-1 (9.75e-3)- |
1.9091e-1 (2.14e-2) |
|
| 300 | 2.0794e-1 (6.58e-3)- |
3.0406e-1 (8.52e-3)- |
1.6129e-1 (5.67e-3)+ |
2.4266e-1 (7.93e-3)- |
1.9760e-1 (1.17e-2) |
|
| 500 | 1.4531e-1 (4.03e-3)+ |
2.1080e-1 (7.63e-3)- |
1.1979e-1 (2.92e-3)+ |
2.0728e-1 (7.50e-3)- |
1.4861e-1 (4.07e-3) |
|
| LSMOP5 | 100 | 8.3054e-1 (1.07e-1)- |
6.9051e+0 (2.78e+0)- |
9.4273e-1 (4.26e-2)- |
9.4593e-1 (2.45e-7)- |
4.9539e-1 (2.21e-1) |
| 200 | 8.0816e-1 (1.39e-1)- |
1.1109e+1 (2.39e+0)- |
9.4592e-1 (1.97e-5)- |
9.4621e-1 (5.34e-5)- |
6.6191e-1 (1.46e-1) |
|
| 300 | 8.6463e-1 (1.07e-1)- |
1.1496e+1 (2.93e+0)- |
9.4592e-1 (1.79e-5)- |
9.3375e-1 (6.25e-2)- |
6.0048e-1 (9.24e-2) |
|
| 500 | 7.1089e-1 (1.33e-1)- |
1.3622e+1 (2.85e+0)- |
9.4592e-1 (1.05e-5)- |
9.3045e-1 (8.07e-2)- |
6.1176e-1 (8.24e-2) |
|
| LSMOP6 | 100 | 9.0306e-1 (6.56e-2)= |
1.5422e+3 (9.47e+2)- |
1.2133e+0 (3.53e-1)- |
1.2524e+0 (2.08e-1)- |
1.1199e+0 (9.86e-1) |
| 200 | 1.0031e+0 (1.33e-1)= |
9.2911e+3 (4.40e+3)- |
2.2314e+0 (9.49e-1)- |
1.5686e+0 (5.63e-2)- |
1.1786e+0 (3.99e-1) |
|
| 300 | 1.3246e+0 (4.60e-1)+ |
1.4594e+4 (5.89e+3)- |
5.4289e+0 (5.42e+0)- |
1.9425e+0 (4.42e-2)= |
1.9822e+0 (6.73e-1) |
|
| 500 | 1.8573e+0 (5.38e-1)+ |
2.1599e+4 (6.50e+3)- |
7.7240e+0 (4.82e+0)- |
2.1589e+0 (3.95e-2)= |
2.2907e+0 (4.91e-1) |
|
| LSMOP7 | 100 | 7.3746e-1 (1.19e-1)= |
2.8586e+0 (3.49e-1)- |
9.4578e-1 (5.24e-4)- |
9.5242e-1 (8.60e-4)- |
7.8228e-1 (1.23e-1) |
| 200 | 8.4547e-1 (1.15e-1)+ |
1.9030e+0 (1.09e-1)- |
9.3269e-1 (5.20e-2)- |
9.5971e-1 (1.29e-3)- |
9.1115e-1 (6.96e-2) |
|
| 300 | 8.0501e-1 (9.47e-2)+ |
1.6070e+0 (4.63e-2)- |
9.2246e-1 (7.07e-2)+ |
9.5926e-1 (8.27e-4)- |
9.3679e-1 (4.12e-2) |
|
| 500 | 8.3604e-1 (1.09e-1)+ |
1.3028e+0 (1.51e-2)- |
9.3036e-1 (4.60e-2)+ |
9.5421e-1 (4.87e-4)- |
9.3717e-1 (3.95e-2) |
|
| LSMOP8 | 100 | 8.2988e-1 (9.51e-2)- |
9.7788e-1 (9.24e-2)- |
9.2364e-1 (1.07e-1)- |
9.4147e-1 (3.53e-2)- |
5.5167e-1 (2.40e-1) |
| 200 | 8.4158e-1 (8.06e-2)= |
9.5006e-1 (6.11e-2)- |
8.1405e-1 (2.10e-1)= |
9.4790e-1 (1.33e-3)- |
8.2316e-1 (1.36e-1) |
|
| 300 | 8.3108e-1 (7.62e-2)= |
9.3423e-1 (7.19e-2)- |
7.3845e-1 (1.98e-1)= |
9.4274e-1 (1.55e-2)- |
8.5669e-1 (5.25e-2) |
|
| 500 | 7.8407e-1 (9.56e-2)+ |
9.0681e-1 (8.70e-2)- |
8.2887e-1 (1.26e-1)= |
9.4631e-1 (1.16e-4)- |
8.8827e-1 (3.30e-2) |
|
| LSMOP9 | 100 | 4.5900e-1 (4.84e-2)- |
2.6293e+1 (8.98e+0)- |
6.1973e-1 (1.19e-1)- |
8.0561e-1 (7.82e-2)- |
4.2327e-1 (2.74e-2) |
| 200 | 4.1844e-1 (1.75e-2)= |
3.4444e+1 (6.32e+0)- |
7.6100e-1 (1.23e-1)- |
8.0113e-1 (7.50e-2)- |
4.2423e-1 (3.56e-2) |
|
| 300 | 4.0938e-1 (1.33e-2)= |
4.4915e+1 (1.05e+1)- |
1.0971e+0 (2.10e-1)- |
8.5657e-1 (2.32e-1)- |
4.0796e-1 (1.59e-2) |
|
| 500 | 4.0158e-1 (8.55e-3)= |
5.2343e+1 (7.37e+0)- |
1.1056e+0 (1.27e-1)- |
8.2076e-1 (6.76e-2)- |
4.0402e-1 (1.34e-2) |
|
| +/-/= | 8/13/15 | 0/36/0 | 7/24/5 | 4/30/2 |
从表 1可以看出,MOEA/D、RVEA、S3-CMA-ES和LMOEA/2s分别获得了17、4、4、11个最佳的IGD值,而CCGDE3未获得任何最佳的IGD值。从表 1中的Wilcoxon秩和检验结果看,相对于MOEA/D、CCGDE3、RVEA、S3-CMA-ES,LSMOEA/2s取得的净胜得分(即对比算法劣于LSMOEA/2s的数目减去对比算法优于LSMOEA/2s的数目)分别为5、36、17和26。综上所述,尽管MOEA/D获得的最佳IGD值的数目多于LSMOEA/2s,但从净胜得分看,LSMOEA/2s优于所有的对比算法。因而不难看出LSMOEA/2s相比于其他4种代表性的对比算法具有显著较优的性能,其获得解集的质量(从收敛性和多样性方面)要明显优于对比算法。究其原因,LSMOEA/2s对大规模决策变量实施两阶段分组,不仅使得算法的结构更加简单,而且节省了大量计算资源,改善了算法的性能,提高了解集的质量。
进一步地,为直观呈现各算法的收敛速度,图 1给出了5种算法在决策变量数目为300维的3-目标LSMOP5测试实例上获得的IGD均值随评估次数增长而变化的轨迹。从图 1可以看出,随着评估次数的增大,5种算法的IGD值总体上在变小,而且在经历3×105次评估后,LSMOEA/2s的IGD值为所有算法的最小值,其次是MOEA/D、S3-CMA-ES和RVEA,CCGDE3的表现是最差的。
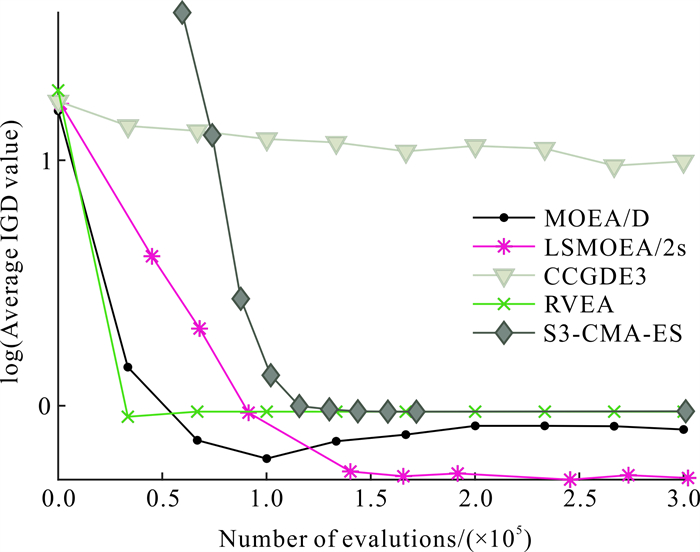
|
| 图 1 5种算法在变量数目为300维的3-目标LSMOP5测试实例上获得的IGD值变化曲线 Fig. 1 Curves of IGD obtained by five algorithms on 3-objective LSMOP5 with 300 decision variables |
图 2给出了5种算法在决策变量数目100维的3-目标LSMOP8测试实例上获得的IGD均值的变化轨迹。从图 2可以看出,在算法运行的前期,MOEA/D和RVEA获得的IGD均值比LSMOEA/2s获得的IGD均值下降的速度快,意味着在算法的初始阶段LSMOEA/2s的性能不如MOEA/D和RVEA。其原因在于:LSMOEA/2s在初始阶段需要花费一定的计算资源用于变量分组,而MOEA/D和RVEA则没有实施变量分组的操作,它们所有的计算资源均用于优化问题的解。因此初始阶段MOEA/D和RVEA的性能要优于LSMOEA/2s。随着进化过程的推进,各算法获得的IGD均值都在逐渐变小,在此过程中LSMOEA/2s获得的IGD均值下降的幅度虽不及MOEA/D和RVEA,但却远胜于CCGDE3和S3-CMA-ES。在评估次数达到1×105时,LSMOEA/2s获得的IGD均值在所有算法中最小,表明LSMOEA/2s此时获得的解集质量最高。究其原因,LSMOEA/2s经过对大规模决策变量分组后,采用MOEA/D方法依次优化各变量子组,使得算法的收敛性和多样性均有较显著的改善,最终获得高质量的解集。综合图 1和图 2的结果来看,对比其他4种算法,LSMOEA/2s具有显著较优的性能,这一点与表 1的实验结果是相吻合的。鉴于IGD指标是度量解集收敛性和多样性的综合指标,其值越小表明算法的性能越好、解集的质量越高。
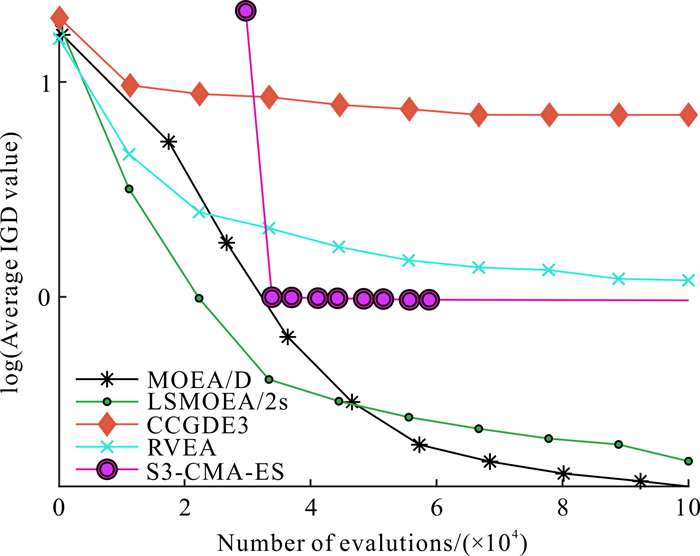
|
| 图 2 5种算法在决策变量数目为100维的3-目标LSMOP8测试实例上获得IGD均值的变化曲线 Fig. 2 Curves of IGD obtained by five algorithms on 3-objective LSMOP8 with 100 decision variables |
4 结论
目前很多LSMOEA在对大规模决策变量实施分组时需要花费大量的计算资源,致使真正用于优化问题解的计算资源相对不足,导致算法的性能尚存较大提升空间。本研究提出一种基于变量两阶段分组的多目标进化算法LSMOEA/2s,其主要特点在于: 首先采用两阶段变量分组方法将大规模决策变量分成独立变量和若干非独立变量子组,然后利用MOEA/D优化所有的独立变量和非独立变量子组。将所提算法与当前本研究领域4种代表性的高效算法(MOEA/DVA、CCGDE3、RVEA、S3-CMAES)一同在100、200、300和500维的3-目标LSMOP1-LSMOP9测试实例上进行IGD性能测试,结果表明所提的LSMOEA/2s具有显著的性能优势。未来将利用更多更困难、更复杂的LSMOP以及现实中的一些应用问题测试并改进本研究算法。
| [1] |
谢承旺, 余伟伟, 郭华, 等. DAV-MOEA: 一种采用动态角度向量支配关系的高维多目标进化算法[J]. 计算机学报, 2022, 45(2): 317-333. |
| [2] |
COOPER I M, JOHN M P, LEWIS R, et al. Optimizing large scale public transport network design problems using mixed-mode parallel multi-objective evolutionary algorithms[C]//Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC). Beijing, China: IEEE, 2014: 2841-2848.
|
| [3] |
QU B Y, ZHOU Q, XIAO J M, et al. Large-scale portfolio optimization using multiobjective evolutionary algorithms and preselection methods[J]. Mathematical Problems in Engineering, 2017, 2017: 4197914. |
| [4] |
DEB K, MYBURGH C. A population-based fast algori- thm for a billion-dimensional resource allocation problem with integer variables[J]. European Journal of Operational Research, 2017, 261(2): 460-474. DOI:10.1016/j.ejor.2017.02.015 |
| [5] |
梁正平, 刘程, 王志强, 等. 基于存档和权值扩展的大规模多目标优化算法[J]. 计算机学报, 2022, 45(5): 951-971. |
| [6] |
OMIDVAR M N, LI X, YANG Z, et al. Cooperative co-evolution for large-scale optimization through more frequent random grouping[C]//Proceedings of the 2010 IEEE Congress on Evolutionary Computation. Barcelona, Spain: IEEE, 2010: 1-8.
|
| [7] |
OMIDVAR M N, YANG M, MEI Y, et al. DG2:a faster and more accurate differential grouping for large-scale black-box optimization[J]. IEEE Transactions on Evolutionary Computation, 2019, 21(6): 929-942. |
| [8] |
MA X, LIU F, QI Y, et al. A multi-objective evolutionary algorithm based on decision variable analyses for multi-objective optimization problems with large-scale variables[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(2): 275-298. DOI:10.1109/TEVC.2015.2455812 |
| [9] |
ZHANG X, TIAN Y, CHENG R, et al. A decision variable clustering-based evolutionary algorithm for large-scale many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2018, 22(1): 97-112. DOI:10.1109/TEVC.2016.2600642 |
| [10] |
HEMPHILL J F. Interpreting the magnitudes of correlation coefficients[J]. American Psychologist, 2003, 58(1): 78-80. DOI:10.1037/0003-066X.58.1.78 |
| [11] |
ZHANG Q, LI H. MOEA/D: a multiobjective evolu- tionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 |
| [12] |
ANTONIO L M, COELLO C A C. Use of cooperative coevolution for solving large scale multiobjective optimization problems[C]//Proceedings of the 2013 IEEE Congress on Evolutionary Computation. Cancun, Mexico: IEEE, 2013: 2758-2765.
|
| [13] |
CHEN R, JIN Y, OLHOFER M, et al. A reference vector guided evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773-791. DOI:10.1109/TEVC.2016.2519378 |
| [14] |
CHEN H, CHENG R, WEN J, et al. Sloving large-scale many-objective optimization problems by covariance matrix adaption evolution strategy with scalable small subpopulations[J]. Information Sciences, 2020, 509: 457-469. DOI:10.1016/j.ins.2018.10.007 |
| [15] |
CHENG R, JIN R C, OLHOFER M, et al. Test problems for large-scale multiobjective and many-objective optimization[J]. IEEE Transactions on Cybernetics, 2017, 47(12): 4108-4121. DOI:10.1109/TCYB.2016.2600577 |
| [16] |
TIAN Y, CHENG R, ZHANG X, et al. PlatEMO: a MATLAB platform for evolutionary multi-objective optimization[J]. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87. |



