位错是金属内部组织的主要缺陷,晶界位错对金属塑性变形有重要影响[1]。一般来说,低角倾斜晶界由垂直于晶界平面的刃位错组成[2]。晶界的位错芯结构可以通过高分辨率透射电子显微镜(HRTEM)直接观察。Hsiung[3]用HRTEM观察发现,单轴压缩下体心立方(BCC)金属Mo在(101)主滑移平面上的位错芯a0/2[111]和a0/2[111]共面位错阵列相互捕获造成{011}异常滑移。江彬彬等[4]观察了金属Nb [001]非对称倾转小角晶界,在外加应力下形成由柏氏矢量为1/2[111]和[111]的刃型位错构成的晶界。在辐照BCC金属变形模拟过程中,1/2 < 111 > 位错与具有柏氏矢量1/2 < 111 > 或[001]辐射诱导的位错环相互作用,这导致在连接处形成[001]位错结[5-7]。并且Haghighat等[8]在模拟中发现施加应变下,两个相交的1/2 < 111 > 位错、一个滑动的刃位错和一个固定的螺位错在刃位错的滑动平面上形成一个[001]混合二元结。陈丽群等[9]利用分子动力学方法研究Fe中4种刃型位错芯结构,其中 < 100 > {010}和 < 100 > {011}位错芯结构有C2V的对称性。Chen等[10]应用分子动力学方法研究 < 100 > {010}和 < 100 > {011}两种位错扭折。除了对BCC晶体进行研究,近年来也有对BCC衍生结构B2结构的研究。例如,Paidar等[11]对B2结构的YAg系统的研究表明,[100]位错芯是紧凑的,解离成1/2[111]和1/2[111]分位错;以及Yan等[12]利用原子模拟FeAl合金研究发现超螺位错芯结构由螺型双三重构型转变为混合三重构型,其核心结构转换会影响滑移和交叉滑移行为。
原子尺度上的模拟方法主要有传统相场(TPF)法[13, 14]、分子动力学(MD)[15]以及晶体相场(PFC)法[16-18]。传统相场法采用的场变量无法展示缺陷的原子细节[19],而对于分子动力学来说,其模拟的时间尺度太小,达不到模拟位错芯的扩展运动的形变时间[20, 21]。晶体相场法[22, 23]是通过分析自由能来进行模拟[1, 24-26],该自由能代表固体晶体相的周期性有序参数分布或液相的恒定参数分布的最小值[27-30],便于观察材料在施加应变的情况下位错的动态过程。之前对BCC晶体的 < 100 > 位错芯研究主要集中在非扩展的位错芯结构,对 < 100 > 位错芯施加应变,观察其芯结构扩展的动态过程的研究少有报道。本文利用PFC法模拟BCC双晶在施加双轴应变下的扩展运动,观察晶界的 < 100 > 位错芯的扩展现象,分析应变对 < 100 > 位错芯扩展的影响,揭示 < 100 > 位错芯的扩展机理。
1 模型与方法 1.1 晶体相场(PFC)法BCC晶体的体系自由能函数,可以用晶体相场模型[31]表示为
| $ \begin{aligned} \Delta F_{i d} & =\int\{[1+n(\vec{r})] \ln [1+n(\vec{r})]- \\ n(\vec{r})\} \mathrm{d} \vec{r} & \approx \int\left[\frac{n(\vec{r})^2}{2}-v \frac{n(\vec{r})^3}{6}+\xi \frac{n(\vec{r})^4}{12}\right] \mathrm{d} \vec{r}, \end{aligned} $ | (1) |
式中,
在总自由能的扩展中,最低限度的粒子相互作用可以包含在过剩能量项中,该项包含了简单的两粒子相关性。在平均参考密度场下,这种相互作用由直接相关函数
| $ \Delta F_{e x}=-\frac{1}{2} \int n(\vec{r}) \int C_2\left(\left|\vec{r}-\vec{r}^{\prime}\right|\right) n\left(\vec{r}^{\prime}\right) \mathrm{d} \vec{r}^{\prime} \mathrm{d} \vec{r}, $ | (2) |
总自由能为
| $ \begin{gathered} \Delta F=\Delta F_{i d}+\Delta F_{e x}= \\ \int\left[\frac{n(\vec{r})^2}{2}-\frac{n(\vec{r})^3}{6}+\frac{n(\vec{r})^4}{12}\right] \mathrm{d} \vec{r}- \\ \frac{1}{2} \int n(\vec{r}) \int C_2\left(\left|\vec{r}-\vec{r}^{\prime}\right|\right) n\left(\vec{r}^{\prime}\right) \mathrm{d} \vec{r}^{\prime} \mathrm{d} \vec{r}_。\end{gathered} $ | (3) |
在改进的双模PFC模型中,Greenwood等[31]提出的直接相关函数形式为
| $ \hat{C}_2(k)=\sum\limits_i e^{-\frac{\sigma^2 k_i^2}{2 \rho_i \beta_i}} e^{-\frac{\left(k-k_i\right)^2}{2 \alpha_i^2}}, $ | (4) |
式中,σ为温度参数,i表示不同的晶面族,ki表示晶面族对应的峰所在位置,与晶面间距成反比,ρ为晶面族的原子密度,β为平面对称数。
将式(4)代入式(3)得到自由能密度函数[32]:
| $ \begin{aligned} & \quad \frac{\Delta F}{V}=\frac{1}{a^3} \int_0^a \int_0^a \int_0^a\left\{\left[\frac{n(x, y, z)^2}{2}-\frac{n(x, y, z)^3}{6}+\right.\right. \\ & \left.\frac{n(x, y, z)^4}{12}\right]-\frac{1}{2} n(x, y, z)\;\; \hat{C_2}(k) \;\;\hat{n}\left(k_x, k_y\right., \\ & \left.\left.k_z\right)\right\} \mathrm{d} x \mathrm{~d} y \mathrm{~d} z, \end{aligned} $ | (5) |
式中,a为晶格常数。对式(5)进行变分,得到系统演化动力学方程:
| $ \frac{\partial n}{\partial t}=\Gamma \nabla^2 \frac{\delta F}{\delta n}=\nabla^2\left(n-\frac{1}{2} n^2+\frac{1}{3} n^3-C_2 n\right) 。$ | (6) |
该动力学方程采用半隐式傅里叶谱解法[33]。
1.2 数值计算与参数设置有序结构相的相互关联能主要存储在直接相关函数Ĉ2(k)低频处的峰中[32],BCC结构92%的关联能体现在{110}晶面族所对应的峰。对BCC晶粒来说单模近似即可,其原子密度为
| $ \begin{gathered} n_{\mathrm{BCC}}(x, y, z)=n_{110}+n, \\ n_{110}=A_{110}\left\{\cos \left(k_0 x\right) \cos \left(k_0 y\right)+\right. \\ \left.\cos \left(k_0 x\right) \cos \left(k_0 z\right)+\cos \left(k_0 y\right) \cos \left(k_0 z\right)\right\}, \end{gathered} $ | (7) |
式中,n为液态的密度,
BCC晶格常数a取值为1,振幅A取值接近稳态密度振幅值时,有助于降低最稳态自由能求解的计算量。在一定峰高条件下,可以通过对系统的自由能进行近似计算,从而得到估算体系最小自由能对应的振幅大小,得到振幅初始值。σ=0时BCC密度场振幅A110=0.132 37。不同参数下的振幅与振幅初始值较为接近。BCC晶粒{110}晶面族直接相关函数峰位置
计算模拟区域为512×512×32的均匀网格,空间步长
|
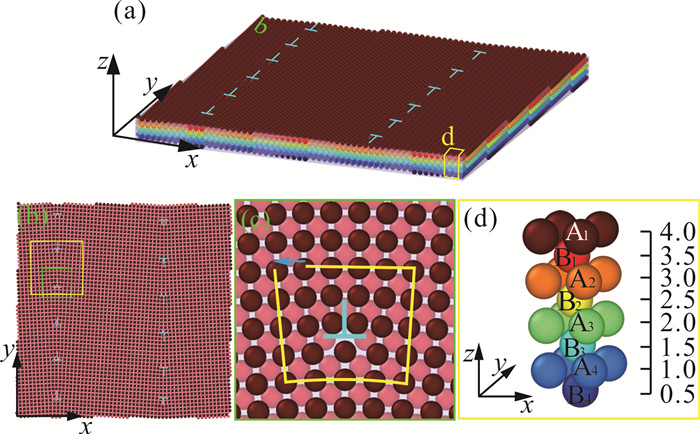
| 图 1 初始时BCC样品图,加载时间t=0, (a)三维BCC双晶样品;(b) (001)面BCC晶界位错排列图;(c) 图(b)中绿色区域的位错放大图:位错区域的原子排列;(d) 图(a)中黄色主体区域的放大图:局部BCC结构 Fig. 1 Initial BCC sample diagram, loading time t=0, (a) Three-dimensional BCC two boundary sample; (b) (001) plane BCC grain boundary dislocations; (c) Enlarged dislocation map of green area in fig.(b): atomic arrangement of dislocation area; (d) Enlarged dislocation map of yellow main area in view (a): local BCC structure |
| $ V=\Delta x \Delta y \Delta z=\Delta x^{\prime} \Delta y^{\prime} \Delta z, $ | (8) |
式中,Δx和Δy为初始空间步长,Δx′和Δy′为变形后的空间步长,可以得到每一步变形后的x和y方向的空间步长分别如下:
| $ \begin{aligned} & \;\;\;\;\;\;\;\;\;\Delta x^{\prime}=\Delta x+n d=\Delta x+n \varepsilon \Delta x \Delta t= \\ & \Delta x(1+n \dot{\varepsilon} \Delta t), \\ & \;\;\;\;\;\;\;\;\;\Delta y^{\prime}=\frac{\Delta x \times \Delta y}{\Delta x^{\prime}}=\frac{\Delta y}{1+n \dot{\varepsilon} \Delta t} 。\end{aligned} $ | (9) |
利用PFC模拟所得的三维BCC样品如图 1(a)所示建立坐标系。为了便于观察原子在z轴的运动情况,给样品表面加上一层透明薄膜。图 1(b)为(001)面的晶界位错排列图,在双晶晶界处各有6个位错,用蓝色“T”表示。放大绿色区域如图 1(c)所示,黄色线表示柏氏回路,蓝色箭头代表柏氏矢量的方向,该柏氏矢量为[100],位错为纯刃位错,且位错线方向为z轴的正方向[001]。放大图 1(a)中黄色方框区域如图 1(d)所示,样品共有8层原子,原子按该球心z轴位置标记颜色,最顶层原子位置z轴坐标为4,颜色为深红色,最底层原子位置z轴坐标为0.5,颜色为深蓝色,原子层之间的间距为0.5。此时把深红色(A1层)、橙色(A2层)、青色(A3层)、蓝色(A4层)看做BCC的顶角原子,红色(B1层)、绿色(B2层)、淡蓝色(B3层)、深蓝色(B4层)看做体心原子,原子层排列为ABABAB⋯。
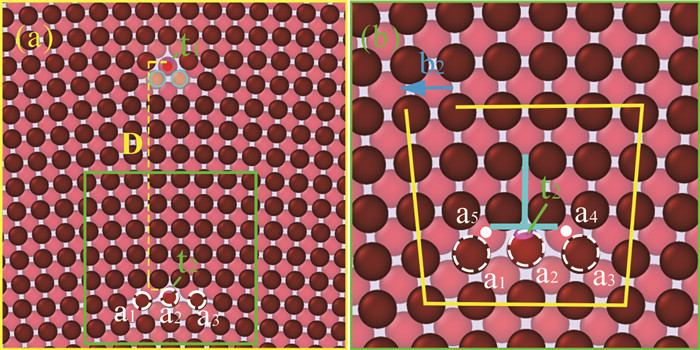
2.2 < 100 > 位错芯扩展的特征为了研究相邻位错间的影响,将图 1(b)中的黄色区域放大[图 2(a)]。经加载23 000步长(ts),如图 2(a)所示,粉色圆表示位错芯b1、b2的位错线t1、t2,其方向是[001] (z轴方向)。b1位错芯区域有2个A1层原子向[001](垂直纸面向外)挤压出去,用淡蓝色圆标出其原来位置,由于周期性边界条件,被挤出的原子回到底部。为了观察位错芯区域原子的特征,放大图 1(b)中的绿色区域[图 2(b)]。图 2(b)中画出了位错芯b2的柏氏回路和柏氏矢量,与初始样品一样。白色虚线圆标记出深红色A1层原子a1、a2、a3,实心圆标记出红色B1层原子a4、a5。原子a2的z轴位置为3.861 5,无缺陷区深红色原子z轴位置为3.985 2-4.000 0,说明a2原子向[001]方向(垂直纸面向里)凹陷。
|
| 图 2 加载时间t=23 000 ts, (a) (001)面位错芯;(b) b2位错芯扩展前的原子排列情况 Fig. 2 Loading time t=23 000 ts, (a) (001) plane dislocation core; (b) The atomic arrangement before the expansion of the b2 dislocation core |
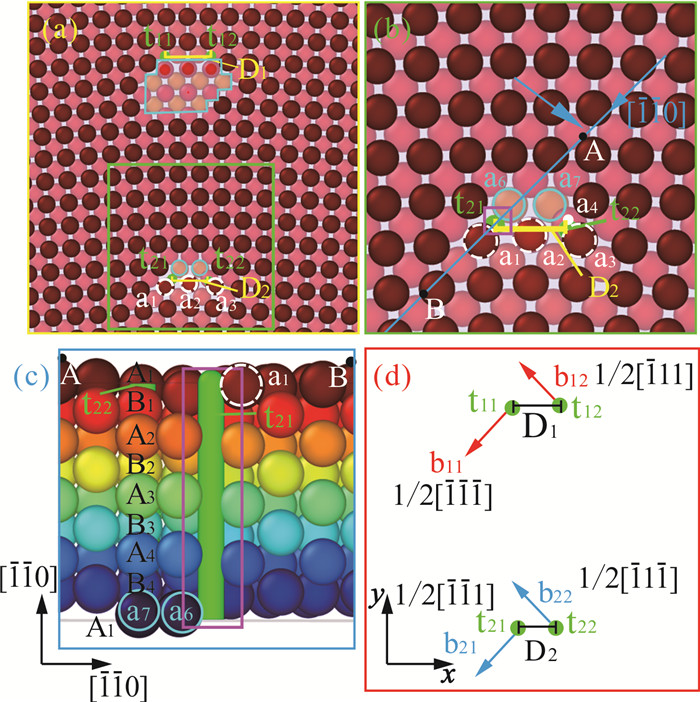
样品加载至23 020 ts时,< 100 > 位错芯开始扩展。如图 3(a)所示,位错b11、b12、b21和b22的位错线t11、t12、t21、t22用绿色圆表示,其方向都是[001](z轴方向)。位错线所在的区域可表示扩展的位错芯的核心区域,b11-b12位错芯半径D1=2a,b21-b22位错芯半径D2=1.5a,b11-b12位错芯区域有7个A1层原子向[001]挤压出去。除了向[001]挤压出的7个原子,淡蓝色区域内其他原子也向[001]挤压。放大绿色区域为图 3(b),由图 3(b)可知原子a5处出现空位(用粉色矩形标出),空位出现是指当前位置原子占位变为0。原子内部发生挤压,达到一定临界条件,此时应变为0.046 04,从而导致b2位错芯扩展。位错线t21在a1和a6原子之间,位错线t22在a3和a4原子之间。原子a1向空隙处移动,移动方向为[111],原子a2向[011]方向移动。如图 3(b)所示沿蓝色线[1 10]方向截面,从箭头所示方向观察该截面原子如图 4(c)。由图 4(c)可知z轴a5原子排处都出现空位(用粉色矩形标出)。此时原子a6、a7的z轴位置为0.103 0和0.100 7。图 3(d)是b11-b12位错芯和b21-b22位错芯区域的位错柏氏矢量图,b11的柏氏矢量为1/2[1 1 1],b12的柏氏矢量为1/2[111];b21的柏氏矢量为1/2[1 11],b22的柏氏矢量为1/2[111]。
|
| 图 3 加载时间t=23 020 ts, (a) (001)面位错芯区域;(b) b2位错芯区域开始扩展时的原子排列情况;(c)为(b) (1-10)面的截面图;(d)为(a)的位错柏氏矢量图 Fig. 3 Loading time t=23 020 ts, (a) (001) dislocation core area; (b) The arrangement of atoms when the dislocation core region of b2 begins to expand; (c) A sectional view of (b) (1-10);(d) The dislocation Bergheim vector diagram of (a) |
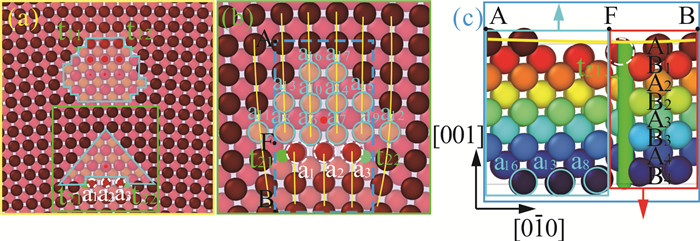
样品加载至23 050 ts时,如图 4(a)所示,位错线t11和t12之间的距离D1=4a,位错线t21和t22之间的距离D2=3a。如图 4(b)所示,位错线t21位于原子a1左下方,位错线t22位于原子a3右下方,b21-b22位错芯区域12个顶角原子向[001]挤压出去,分别是a6、a7、a8、a9、a10、a11、a12、a13、a14、a15、a16和a17原子。位错线的扩展规律为b21和b22分别先向[100](或[100])移动a/2,再向[010]方向移动a/2。图 4(c)为图 4(b)中蓝色虚线框AB处的(100)截面,红色矩形区域原子整体向[001]方向移动(图中红色箭头所示),a1、a2、a3原子包含在其中。淡蓝色矩形区域向[001]方向移动(图中淡蓝色箭头所示),反向移动的原子运动会导致原子层错排。
|
| 图 4 加载时间t=23 050 ts,(a) (001)面位错芯区域;(b)为(a)绿色区域放大图;(c)为(b)蓝色虚线框AB处(100)截面 Fig. 4 Loading time t=23 050 ts, (a) Dislocation core area of (001) plane; (b) Enlarged view of (a) green area; (c) Section (100) of (b) blue dotted line box AB |
样品加载至23 070 ts时,如图 5(a)所示,位错线t11和t12之间的距离D1=5a,位错线t21和t22之间的距离为D2=4a。由于蓝线围成的区域的顶角原子向[001]挤压出去,导致b11-b12位错芯区域与b21-b22位错芯区域扩展连成为一个整体,即位错团区域,该区域由4个不同的1/2 < 111 > 柏氏矢量组成。位错团区域中60个顶角原子向[001]挤压出去,该区域的其他层原子也向[001]凸出。位错芯上方的原子排(黄线表示)为7条,位错芯下方的原子排(黄线表示)为5条,上方原子排与下方原子排的比值为7∶5 [图 5(a)]。图 5(b)为图 5(a)中绿色区域的放大图,图中a1、a2、a3原子的z轴位置分别为3.746 5、3.735 4、3.743 9,其他正常A1层顶角原子之间z轴位置相差0.25左右,说明这3个原子向[001]方向凹陷严重。B1层原子a18、a19、a20也向[001]方向移动明显。图 5(c)为图 5(b)中蓝色虚线框AB处的(100)截面,随着位错芯扩展,由图 5(c)可见,由淡蓝色框里的B1层原子向[001]方向移动(如图中淡蓝色箭头所示),红色框里A1层原子向[001]方向移动(如图中红色箭头所示),导致B1层原子和A1层原子组合成新的一层(图中绿线所示),原子层错排,但是原子层排列依旧是ABABAB⋯结构。

|
| 图 5 加载时间t=23 070 ts,(a) (001)面位错芯区域;(b)为(a)绿色区域放大图;(c)为(b)蓝色虚线框AB处(100)截面 Fig. 5 Loading time t=23 070 ts, (a) Dislocation core area of (001) plane; (b) Enlarged view of (a) green area; (c) Section (100) at (b) blue dotted box AB |
2.3 扩展位错芯的柏氏矢量组态结构
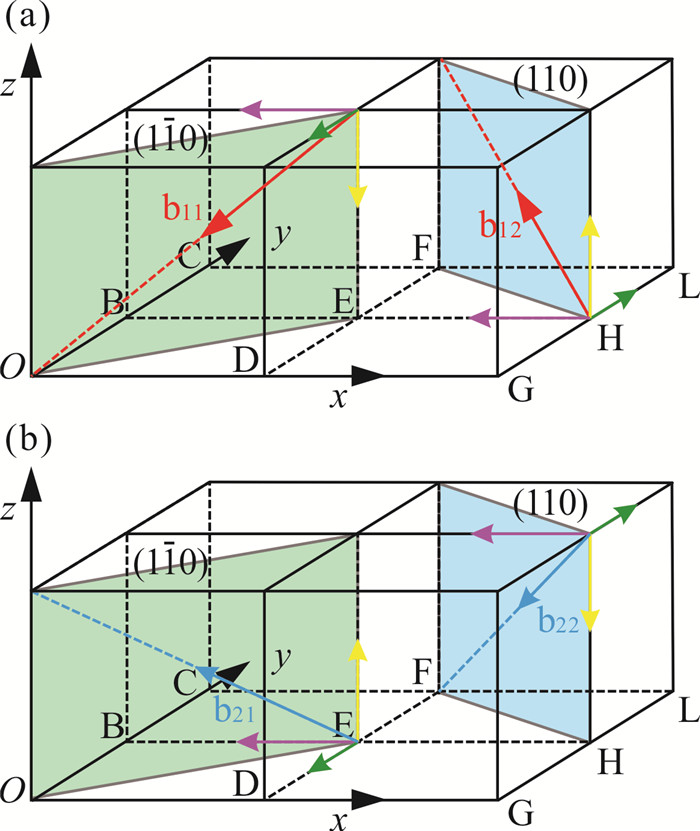
位错反应能否进行要看几何条件和能量条件。从几何条件看,如图 6所示,b11的柏氏矢量为1/2[1 1 1]、b12的柏氏矢量为1/2[111]、b21的柏氏矢量为1/2[1 11]、b22的柏氏矢量为1/2[111],b11、b12、b21、b22正好就是BCC体心的4个对角线方向。b11和b21的滑移面为(110),滑移方向为 < 111 > ;b12和b22的滑移面为(110),滑移方向为 < 111 > 。按x、y、z轴正交分解,粉色箭头为x轴上分解的分位错,绿色箭头为y轴上分解的分位错,黄色箭头为z轴上分解的分位错。由图 6可知,y轴和z轴上的分位错相互抵消,x轴上的分位错之和为[100],符合位错几何条件,位错反应方程如下。
| $ \begin{aligned} b_1 & \rightarrow b_{11}+b_{12}:[\overline{1} 00] \rightarrow \frac{1}{2}[\overline{1} \overline{1} \overline{1}]+\frac{1}{2}[\overline{1} 11], \\ b_2 & \rightarrow b_{21}+b_{22}:[\overline{1} 00] \rightarrow \frac{1}{2}[\overline{1} \overline{1} 1]+\frac{1}{2}[\overline{1} 1 \overline{1}]。\end{aligned} $ |
从能量条件看:E100 < 2E111,不满足条件,位错反应不能发生。但由于施加应变,能量有外条件要求
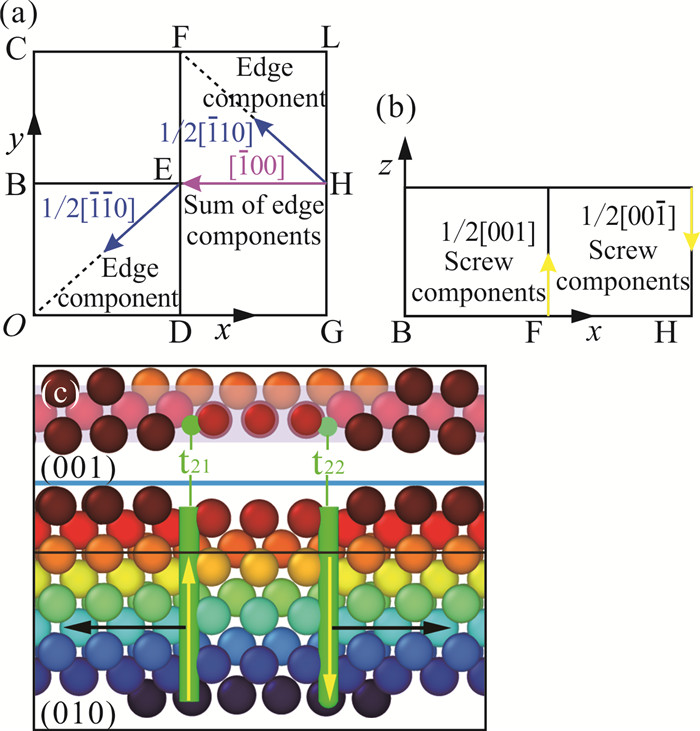
位错除了根据其几何意义进行分解外,还可以根据其物理意义进行分解。图 7(a)为位错在(001)面的投影,b21位错的刃分量为1/2[110],b22位错的刃分量为1/2[110],刃位错之和为[100]。图 7(b)为位错在(100)面的投影,b21螺分量为1/2[001],b22螺分量为1/2[001]。通过计算得出,b12和b21柏氏矢量与位错线的夹角为54.74°,b11和b22柏氏矢量与位错线的夹角为125.26°。按照几何条件,螺分量之和为0。但是由于位错芯已经扩展,相反的两个螺分量不会抵消,而是形成原子级台阶。并且如图 7(c)所示,黄色箭头为螺分量,黑色箭头为螺分量的运动方向,黑色实线为A2层原子正常位置,由图 7(c)可知,位错线t21和t22之间的原子不在黑色实线上,表明形成了台阶。随着位错芯的扩展,台阶的宽度会变大。螺分量是位错芯在扩展中造成原子错排的原因。
|
| 图 6 (a) b11和b12的空间中的柏氏矢量;(b) b21和b22的空间中的柏氏矢量 Fig. 6 (a) Burgers vector in the space of b11 and b12; (b) Burgers vector in the spaces of b21 and b22 |
|
| 图 7 (a) b21和b22位错在(001)面的投影;(b) b21和b22位错在(100)面的投影;(c)加载时间23 050 ts时的(001)面与其截面(010)面 Fig. 7 (a) Projection of dislocation b21 and b22 on the (001) plane; (b) Projection of b21 and b22 dislocations on the (100) plane; (c) When the loading time is 23 050 ts, the (001) side is the same as the (010) side |
2.4 扩展位错芯的应变场分析
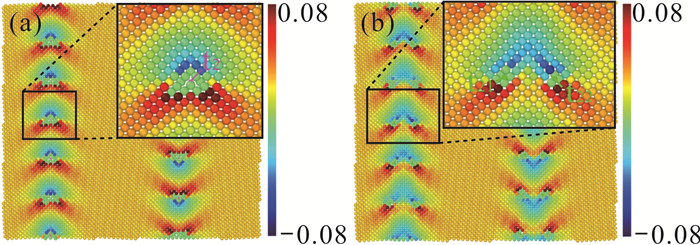
使用OVITO软件[35]模拟实验样品的εxx应变场分布。使用OVITO软件中的Elastic strain功能[36]来计算样品的应变分布情况。由于PFC的密度场是以密度波的形式存在,所以选择密度场峰点的位置作为原子的位置。图 8(a)为加载时间t=23 000 ts时的应变场,其中放大区域为b2位错芯区域的应变图,右边色标上的值对应图中颜色所代表的应变值,拉伸应变区域为黄色至红色,对应值为0-0.08;压缩应变区域为淡蓝色至深蓝色,对应值为-0.08-0;绿色为无应变区域,数轴为0。多余原子面区域颜色为蓝色,代表此区域原子受到压应变作用,位错头部区域颜色为红色,则区域受到拉应变作用,有利于位错的扩展。图 8(b)表示 < 100 > 位错芯扩展后t=23 050 ts时样品的应变分布图,如图所示,受到压应变作用的蓝色原子区域面积扩大,受到拉应变作用的位错头部区域原子颜色为红色,与23 000 ts的应变相比较,可以看到位错头部红色原子区域分开。
|
| 图 8 BCC样品的εxx应变场分布图,(a)加载时间t=23 000 ts;(b)加载时间t=23 050 ts Fig. 8 εxx strain field distribution diagram of BCC sample, (a) Loading time t=23 000 ts; (b) Loading time t=23 050 ts |
3 结论
① 在施加x轴拉应变、y轴压应变下,晶界位错出现空位,给 < 100 > 位错芯扩展提供了条件,< 100 > 位错芯扩展为1/2 < 111 > 组成的扩展位错芯结构,最终两个晶界位错发生合并,成为一个位错团,且由4个柏氏矢量不同的1/2 < 111 > 位错组成。
② 在施加应变下,< 100 > 位错芯的扩展存在分解反应,可分解成1/2[111]和1/2[111],位错线依旧为[001]。1/2[111]和1/2[111]是混合位错。柏氏矢量与位错线的夹角分别为54.74°和125.26°。其螺分量分别为1/2[001]和1/2[001]。
③ < 100 > 位错芯的应变场分布情况:多余原子面区域原子受到压应变作用,位错头部区域原子受到拉应变作用。位错芯扩展后位错头部拉应变区域分开,多余原子面压应变作用区域面积扩大。
| [1] |
高英俊, 卢昱江, 孔令一, 等. 晶体相场模型及其在材料微结构演化中的应用[J]. 金属学报, 2018, 54(2): 278-292. |
| [2] |
FURUSHIMA Y, ARAKAWA Y, NAKAMURA A, et al. Nonstoichiometric [012] dislocation in strontium titanate[J]. Acta Materialia, 2017, 135: 103-111. DOI:10.1016/j.actamat.2017.06.017 |
| [3] |
HSIUNG L L. On the mechanism of anomalous slip in bcc metals[J]. Materials Science and Engineering A, 2010, 528(1): 329-337. DOI:10.1016/j.msea.2010.09.017 |
| [4] |
江彬彬, 杜奎, 叶恒强. 体心立方金属铌中小角度晶界分解的原位电子显微学表征[J]. 电子显微学报, 2019, 38(2): 102-106. |
| [5] |
TERENTYEV D A, OSETSKY Y N, BACON D J. Effects of temperature on structure and mobility of the < 100 > edge dislocation in body-centred cubic iron[J]. Acta Materialia, 2010, 58(7): 2477-2482. DOI:10.1016/j.actamat.2009.12.033 |
| [6] |
BACON D J, OSETSKY Y N, RONG Z. Computer simulation of reactions between an edge dislocation and glissile self-interstitial clusters in iron[J]. Philosophical Magazine, 2006, 86(25/26): 3921-3926. |
| [7] |
XU H X, STOLLER R E, OSETSKY Y N, et al. Solving the puzzle of < 100 > interstitial loop formation in bcc iron[J]. Physical Review Letters, 2013, 110(26): 265503. DOI:10.1103/PhysRevLett.110.265503 |
| [8] |
HAGHIGHAT S M H, SCHÄUBLIN R, RAABE D. Atomistic simulation of the a0 < 100 > binary junction formation and its unzipping in body-centered cubic iron[J]. Acta Materialia, 2014, 64: 24-32. DOI:10.1016/j.actamat.2013.11.037 |
| [9] |
陈丽群, 王崇愚, 于涛. bcc Fe中刃型位错的结构及能量学研究[J]. 物理学报, 2006, 55(11): 5980-5986. |
| [10] |
CHEN L Q, WANG C Y, YU T. Molecular dynamics simulation of kink in < 100 > edge dislocation in body centred cubic iron[J]. Chinese Science Bulletin, 2007, 52(16): 2291-2296. DOI:10.1007/s11434-007-0323-9 |
| [11] |
PAIDAR V, ČÁK M. Three types of dislocation core structure in B2 alloys[J]. Intermetallics, 2016, 73: 21-25. DOI:10.1016/j.intermet.2016.02.007 |
| [12] |
YAN J X, ZHANG Z J, LI K Q, et al. Core structures and planar faults associated with < 111 > screw superdislocations in B2 alloys[J]. Intermetallics, 2019, 110: 106470. DOI:10.1016/j.intermet.2019.04.013 |
| [13] |
FAN D, CHEN L Q. Computer simulation of grain growth using a continuum field model[J]. Acta Materialia, 1997, 45(2): 611-622. DOI:10.1016/S1359-6454(96)00200-5 |
| [14] |
STEINBACH I. Phase-field model for microstructure evolution at the mesoscopic scale[J]. Annual Review of Materials Research, 2013, 43: 89-107. DOI:10.1146/annurev-matsci-071312-121703 |
| [15] |
LIU J, ZHAO J Z, HU Z Q. Kinetic details of the nucleation in supercooled liquid metals[J]. Applied Physics Letters, 2006, 89(3): 031903. DOI:10.1063/1.2222335 |
| [16] |
WU K A, VOORHEES P W. Phase field crystal simulations of nanocrystalline grain growth in two dimensions[J]. Acta Materialia, 2012, 60(1): 407-419. DOI:10.1016/j.actamat.2011.09.035 |
| [17] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70: 051605. DOI:10.1103/PhysRevE.70.051605 |
| [18] |
GREENWOOD M, PROVATAS N, ROTTLER J. Free energy functionals for efficient phase field crystal modeling of structural phase transformations[J]. Physical Review Letters, 2010, 105(4): 45702. DOI:10.1103/PhysRevLett.105.045702 |
| [19] |
WILLIAMS P L, MISHIN Y. Thermodynamics of grain boundary premelting in alloys.Ⅱ.Atomistic simulation[J]. Acta Materialia, 2009, 57(13): 3786-3794. DOI:10.1016/j.actamat.2009.04.037 |
| [20] |
STEFANOVIC P, HAATAJA M, PROVATAS N. Phase field crystal study of deformation and plasticity in nanocrystalline materials[J]. Physical Review E, 2009, 80(4): 46107. DOI:10.1103/PhysRevE.80.046107 |
| [21] |
QI Y, KRAJEWSKI P E. Molecular dynamics simulations of grain boundary sliding: the effect of stress and boundary misorientation[J]. Acta Materialia, 2007, 55(5): 1555-1563. DOI:10.1016/j.actamat.2006.10.016 |
| [22] |
DENG Q Q, GAO Y, LIAO K, et al. Energy model of transformation of two-time decomposition mode of dislocation structure at triple junction: ultra-fine grained materials[J]. Mechanics of Materials, 2022, 173: 104438. DOI:10.1016/j.mechmat.2022.104438 |
| [23] |
LI Y X, GAO Y J, YI X A, et al. Phase field crystal simulation of gap healing at nanoscale[J]. Modelling and Simulation in Materials Science and Engineering, 2022, 30(6): 064004. DOI:10.1088/1361-651X/ac8174 |
| [24] |
叶里, 胡绪志, 黄礼琳, 等. 拉应力作用下晶界位错运动过程的晶体相场模拟[J]. 广西科学, 2016, 23(5): 470-473, 484. DOI:10.13656/j.cnki.gxkx.20161121.016 |
| [25] |
宁岁婷, 胡绪志, 黄礼琳, 等. 三角缺口与圆形缺口起裂和裂纹扩展的晶体相场模拟[J]. 广西科学, 2017, 24(6): 540-544, 550. |
| [26] |
邓力滔, 卢昱江, 刘哲源, 等. 晶体相场法模拟晶界萌生裂纹扩展机理[J]. 广西科学, 2018, 25(6): 658-662. DOI:10.13656/j.cnki.gxkx.20181225.002 |
| [27] |
BERRY J, PROVATAS N, ROTTLER J, et al. Defect stability in phase-field crystal models: stacking faults and partial dislocations[J]. Physical Review B, 2012, 86(22): 224112. DOI:10.1103/PhysRevB.86.224112 |
| [28] |
BERRY J, PROVATAS N, ROTTLER J, et al. Phase field crystal modeling as a unified atomistic approach to defect dynamics[J]. Physical Review B, 2014, 89(21): 214117. DOI:10.1103/PhysRevB.89.214117 |
| [29] |
LIU Z Y, GAO Y J, DENG Q Q, et al. A nanoscale study of nucleation and propagation of zener types cracks at dislocations: phase field crystal model[J]. Computational Materials Science, 2020, 179: 109640. DOI:10.1016/j.commatsci.2020.109640 |
| [30] |
HUANG L L, GAO Y J, DENG Q Q, et al. A study of relationship between dislocation configuration of nanocrack and brittle-ductile mode of fracture: atomistic modeling[J]. Computational Materials Science, 2020, 173: 109413. DOI:10.1016/j.commatsci.2019.109413 |
| [31] |
GREENWOOD M, ROTTLER J, PROVATAS N. Phase-field-crystal methodology for modeling of structural transformations[J]. Physical Review E, 2011, 83(3): 031601. |
| [32] |
郭灿, 王志军, 王锦程, 等. 直接相关函数对双模晶体相场模型相图的影响[J]. 物理学报, 2013, 62(10): 419-426. |
| [33] |
CHEN L Q, SHEN J. Applications of semi-implicit Fourier-spectral method to phase field equations[J]. Computer Physics Communications, 1998, 108(2/3): 147-158. |
| [34] |
HIROUCHI T, TAKAKI T, TOMITA Y. Development of numerical scheme for phase field crystal deformation simulation[J]. Computational Materials Science, 2009, 44(4): 1192-1197. DOI:10.1016/j.commatsci.2008.08.001 |
| [35] |
STUKOWSKI A. Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool[J]. Modelling and Simulation in Materials Science and Engineering, 2010, 18(1): 015012. DOI:10.1088/0965-0393/18/1/015012 |
| [36] |
STUKOWSKI A, ARSENLIS A. On the elastic-plastic decomposition of crystal deformation at the atomic scale[J]. Modelling and Simulation in Materials Science and Engineering, 2012, 20(3): 035012. DOI:10.1088/0965-0393/20/3/035012 |



