裂纹等微结构对材料性质有重要的影响,如裂纹扩展会引起材料的断裂等。为防止裂纹的扩展以及提高材料的使用寿命,人们开始重视孔洞裂纹愈合研究。例如,对陶瓷[1-3]、聚合物[4, 5]和金属材料[6]进行加热可使其裂纹愈合;对TiB2-SiC陶瓷[7]可以通过氧化反应形成氧化膜来防止其表面氧化,而对聚合物[8]则可通过氧化还原反应刺激溶胶-凝胶相变来控制样品愈合;Kumar等[9]使用脉冲电流修复钢疲劳裂纹孔洞,Chen等[10]采用高温空气热处理方法研究Al2O3/TiC/TiB2陶瓷材料的裂纹愈合效果,等等。但在严苛的实验条件如高温、高压下,宏观实验过程中不能实时观察材料微观结构的变化情况,而计算机模拟方法具有安全性高且可以补充实验细节等优点,因此已成为研究材料微观结构演化的有效方法之一。例如,Li等[11]通过分子动力学模拟实现了剪切力作用下铜板的裂纹愈合,Li等[12]通过分子动力学模拟研究了压应力作用下金属铜内椭球孔洞的愈合,Xu等[13]通过向错诱导实现纳米晶材料中的孔洞裂纹愈合。分子动力学模拟[14, 15]是研究材料微观结构的重要方法之一,但该方法适用的时间尺度主要是原子振动的时间尺度(10-15-10-12 s),难以拓展到原子扩散的时间尺度(10-6 s),导致模拟的加载应变速率达到107-109量级[16],远远偏离实际工业生产的应变速率(10-2 s-1)。
本研究使用晶体相场模型(Phase Field Crystal model, PFC模型)对材料纳米孔洞愈合特征进行分析。PFC模型是Elder等[17, 18]基于密度泛函理论提出的,该模型已有广泛应用,如材料的外延生长[19, 20]、相结构转变[21-23]、裂纹扩展[24-26]等现象的研究,但是目前有关PFC模型模拟孔洞愈合方面的文献报道较少。本研究利用PFC模型模拟在温度不变的情况下对样品施加压应变的纳米孔洞修复实验,对孔洞愈合的微观细节进行观察,旨在揭示受压应变下的材料纳米孔洞愈合的微观机理。
1 模拟方法 1.1 PFC模型PFC模型不仅能够揭示晶体点阵周期性结构特性,而且还能模拟原子尺度下的纳微结构演化[27-29]。对于固态晶体材料,可引入周期性原子密度函数ρ(r)作为场变量。原子密度函数的极大值对应于原子点阵的中心位置,其原子的位置呈周期性排列,则周期性原子密度函数ρ(r)的表达式为
| $ \rho(r)=\sum\limits_\nolimits {n \cdot m} a_{n, m} e^{i G \cdot r}+\rho_0, $ | (1) |
式中,等号右边第1项反映了晶格原子的周期性排列结构特征,其中an, m为Fourier系数,i为虚数,G为倒格子矢量,r为空间坐标矢量;第2项ρ0为均匀相(如液相),表明原子密度均匀分布。系统无量纲的自由能函数可以写成:
| $ F=\int\left\{\frac{\rho}{2}\left[\gamma+\left(1+\nabla^2\right)^2\right] \rho+\frac{\rho^4}{4}\right\} \mathrm{d} r^3, $ | (2) |
式中,γ为与温度有关的参数,
| $ \begin{aligned} & \rho(r)=A\left[\cos (q x) \cos \left(\frac{q y}{\sqrt{3}}\right)-\frac{1}{2} \cos \left(\frac{2 q y}{\sqrt{3}}\right)\right]+ \\ & \rho_0, \end{aligned} $ | (3) |
式中,
| $ \frac{\partial \rho}{\partial t}=\nabla^2 \frac{\delta F}{\delta \rho}, $ | (4) |
式中,t为时间变量。采用半隐式傅里叶谱方法[31]求解该动力学演化方程。
1.2 模拟实验样品的制备模拟实验样品区域的边界条件设置成周期性边界条件,模拟区域为1 024×2 048的均匀网格,空间步长
| $ \Delta x^{\prime}=\Delta x, $ | (5) |
| $ \Delta y^{\prime}=\frac{\Delta y}{1+\varepsilon}=\frac{\Delta y}{1+n \dot{\varepsilon} \Delta t} 。$ | (6) |
如图 1所示,蓝色虚线表示总体系的自由能变化;黑色实线是自由能斜率曲线,表示样品在施加压应变过程中体系内部平均应力的变化趋势。曲线上的点(A0, A, B, C……)对应后续图中的样品孔洞愈合演化时刻。自由能斜率曲线A0点到A点阶段表示随着压应变的持续施加,曲线线性上升,该阶段变形服从虎克定律,表现为弹性变形。B点到K点阶段表示位错形核并发射,孔洞收缩,该过程表现为塑性变形。K点到L点阶段表示孔洞修复完成。后续按3个阶段分析材料纳米孔洞愈合的模拟结果。
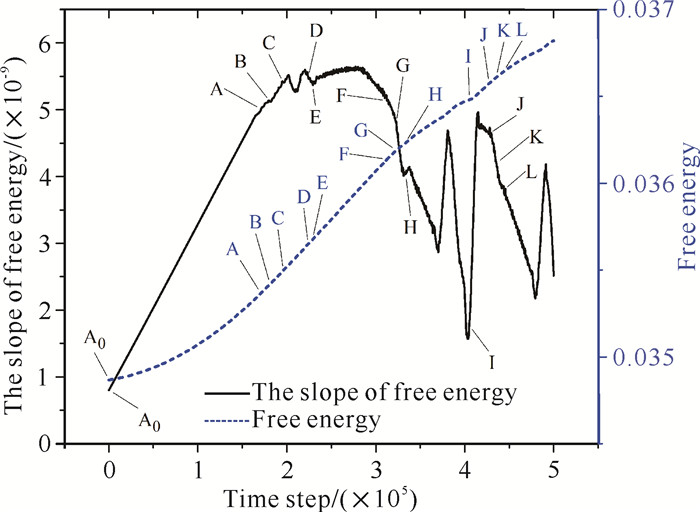
|
| 图 1 自由能曲线和自由能斜率曲线 Fig. 1 Free energy curve and the slope of free energy curve |
2.1 纳米孔洞的形貌变化
图 2(a)为未加力前初始孔洞样品情况,对应于图 1中A0点。在样品中心处预设一缺口,插图为缺口放大示意图,黄线区域即是缺口边界,该缺口是边长为4个格点的正六边形(l=4a)。由该插图放大图可知,缺口竖直方向厚度为7层原子层,用蓝色箭头标出。从时刻A0点开始,沿y轴方向在缺口处加压应变。在A0点→A点的过程中,随着压应变的增加,系统的自由能呈单调上升趋势。图 2(b)对应于图 1中A点时的样品情况。当加力时间为171 000步时,在缺口竖直方向上的第3层和第5层原子面开始凸出,第4层原子面凹陷,缺口呈阶梯状分布。如图 2(b)的插图(A2)所示,样品中心预设的缺口两侧出现两组位错对,用粉色的“⊥”刃型位错表示,并在附近用蓝色辅助线显示出位错的位置。
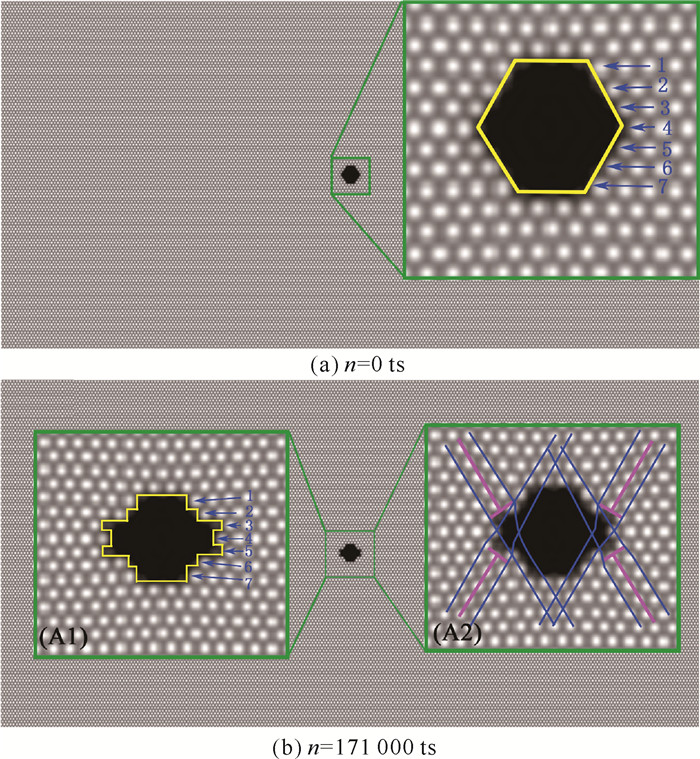
|
| 图 2 A0点初始孔洞样品(a)及A点样品的演化图(b) Fig. 2 Initial hole sample at point A0 (a) and evolution diagram of the sample at point A (b) |
2.2 位错发射与孔洞收缩
图 3对应图 1中B点时的样品情况。如图 3(B1)所示,在181 000步时缺口的原第3层和原第5层原子面向第4层原子面挤压,原第4层原子面在x方向上两侧扩展并形成第一组位错团,原第4层原子面开始消失,整个缺口面积减小。图 3(B2)为将要发射的两个位错团,该位错团分别由3个位错组成,用粉色的“⊥”刃型位错表示。

|
| 图 3 B点的样品演化图(n=181 000 ts) Fig. 3 Evolution diagram of the sample at point B (n=181 000 ts) |
图 4(a)对应图 1中C点时的样品情况。如图 4(a)所示,在压应变挤压作用下,缺口的第3层和第4层原子面开始发生扩展,长出凸口。B点时形成的位错团以位错发射形式从凸口两侧沿x轴方向水平滑移,构成滑开型位错。如图 4(a)的插图(C2)所示,a1、a2分别表示发射的2个位错团。位错发射后,两侧的a1、a2位错团与缺口之间出现狭缝连线区域,该区域形成4个双位错对。位错团a1、a2的滑移方向与压应变方向垂直,如黑色箭头所示。图 4(b)为C点时所对应样品的εyy应变分布情况,拉应变区域为黄色至红色,对应值为0-0.2;压应变区域为淡蓝色至深紫色,对应值为-0.2-0;绿色为无应变区域,数值为0,后续图中的应变场以该色标为准。位错团a1、a2的多余原子面区域颜色为蓝色,代表此区域原子受到压应变作用;位错团头部区域颜色为红色,则该区域受到拉应变作用。图 4(b)插图(C1)是εyy应变分布图叠加原子密度的放大图,黄色线围成的孔洞区域在εyy应变分布图中本应该是绿色无应变区域,但由于初始设置孔洞的密度并不为零,所以该区域存在应变。压应变在缺口附近的位错团处形成应变集中,提供位错团滑移所需要的能量。作用在位错团上的总应力为斥力,当斥力大于滑移阻力时位错团从凸口处发射,位错团运动方向与被修复原子面方向保持一致,位错团做加速运动远离凸口。
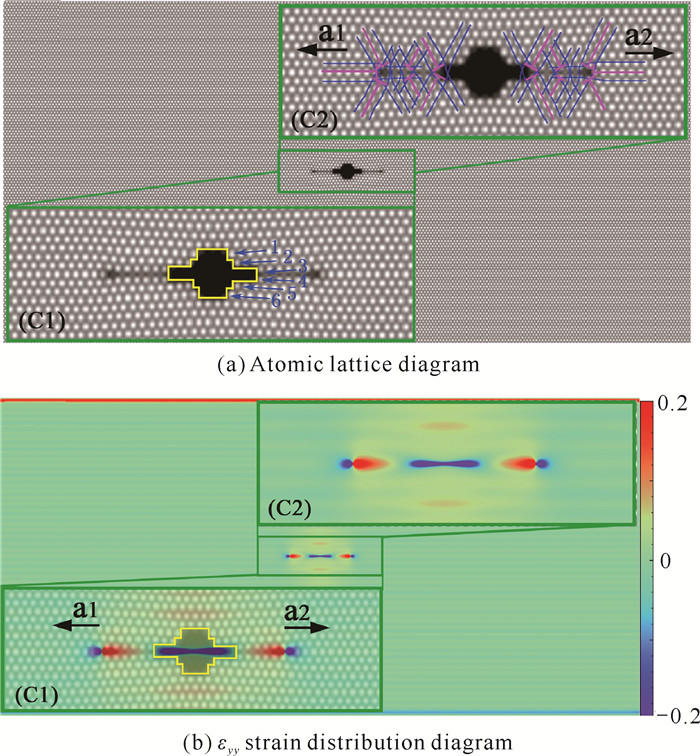
|
| 图 4 C点的样品演化图(n=196 000 ts) Fig. 4 Evolution diagram of the sample at point C(n=196 000 ts) |
如图 5(a)所示,随着压应变的持续作用,位错团a1、a2与缺口之间的狭缝连线区域愈合,表面能下降,第一层原子面修复过程结束。孔洞的第3层和第4层原子面持续扩展并形成梯形结构。如图 5(a)的插图(D2)所示,在凸口处狭缝区域愈合过程中,位错团a1、a2转变成由两个位错组成的位错对。在裂纹扩展尖端形成位错对b1、b2,开启第二层原子面修复过程。如图 5(b)所示,已发射位错对仍处于应力集中状态,受压应变作用。

|
| 图 5 D点的样品演化图(n=224 000 ts) Fig. 5 Evolution diagram of the sample at point D (n=224 000 ts) |
图 6(a)表示孔洞的第二原子面收缩完成。由图 6(a)的插图(E1)可见,样品中心缺口厚度降低为5层原子面,形成边长为3个格点的正六边形。在图 6(a)的插图(E2)中,共发射4个位错对a1、a2、b1和b2,位错对沿x轴方向滑移。受压应变作用,b1和b2位错对与缺口之间的表面缝隙提前愈合。图 6(b)中缺口两侧的位错对a1、a2、b1和b2之间的距离逐渐增加。如图 6(b)的插图(G6)所示,缺口的第2层和第3层原子面开始扩展,此时缺口扩展的长度比之前扩展的长度长。凸口扩展的尖端形成2个位错对c1、c2,在凸口扩展的尖端和初始端之间还存在2个位错,凸口形成的位错对会对凸口产生一个回复力,因此扩展的尖端宽度大于初始端宽度。随着压应变的增加,作用在位错上的总应力增大,当其大于滑移阻力时,缺口扩展的尖端处会发射位错对c1、c2,该过程与修复第一层原子面阶段相似。凸口发射位错后,在压应变作用下,裂纹张开位移减小,凸口初始端与尖端之间的间隙提前愈合,导致凸口扩展的驱动力下降,凸口扩展区域被逐渐挤压而消失,而凸口的闭合导致自由能增长趋势的降低。E点到G点阶段,在凸口附近的区域内,由于位错受吸引力影响很难发射,因此位错发射需要克服一定的晶格阻力。

|
| 图 6 样品演化图 Fig. 6 Evolution diagram of the sample |
图 7(a)对应图 1中H点的位置情况。如图 7(a)的插图(H5)所示,G→H阶段持续进行凸口扩展区域的愈合过程,样品表面能减少,发射位错对间的距离与被修复原子面克服滑移阻力所需做功增加,生成新的位错对d1和d2。新位错对发射前,凸口的扩展区域便已经愈合。图 7(a)的插图(H6)显示出样品中心缺口厚度减少为3层原子面。图 7(b)中有8处应力集中处,当压应变达到发射位错的临界应力强度时,开始发射位错。

|
| 图 7 H点的样品演化图(n=333 500 ts) Fig. 7 Evolution diagram of the sample at point H (n=333 500 ts) |
图 8(a)对应图 1中I点的位置情况。由图 8(a)中插图可知,由于样品的边界性周期条件,发射的位错对a1和a2与边界接触后运动方向发生变化,导致两者按原来相反的滑移方向运动。如图 8(a)的插图(I7)和(I8)中所示,孔洞已经收缩为两层原子面,上底为4个格点,下底为3个格点,发射新的位错对e1、e2,在缺口底部存在两个位错。第5层原子面修复过程非常短,没有产生大幅度的裂纹扩展现象。图 8(b)中有10处应力集中区域,这些区域间的距离随应变施加而增加。

|
| 图 8 I点的样品演化图(n=405 000 ts) Fig. 8 Evolution diagram of the sample at point I (n=405 000 ts) |
图 9对应图 1中J点的位置情况。如图 9所示,中心缺口形状变为上底为3个格点、下底为5个格点的双层阶梯。I→J点过程孔洞的第一层原子面收缩,第二层原子面发生扩展,并在端点处生成2个位错对。
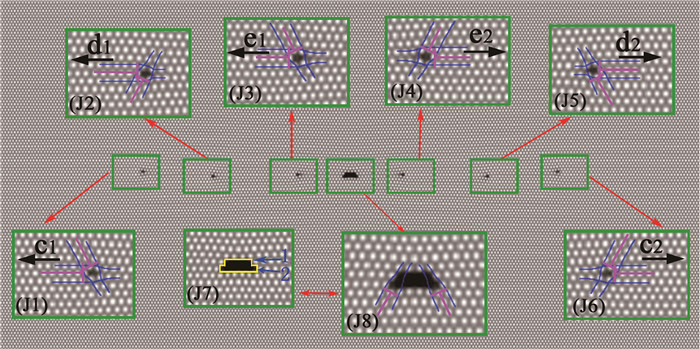
|
| 图 9 J点的样品演化图(n=427 000 ts) Fig. 9 Evolution diagram of the sample at point J (n=427 000 ts) |
2.3 孔洞修复完成
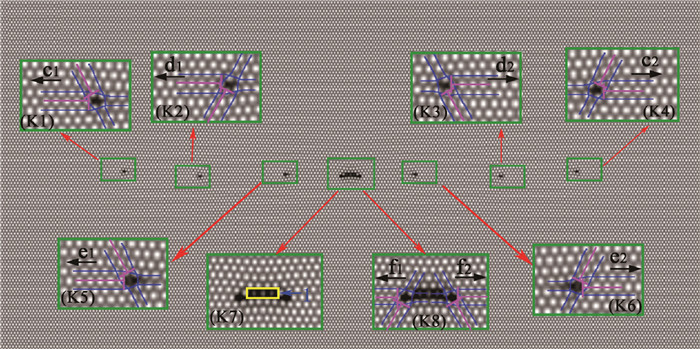
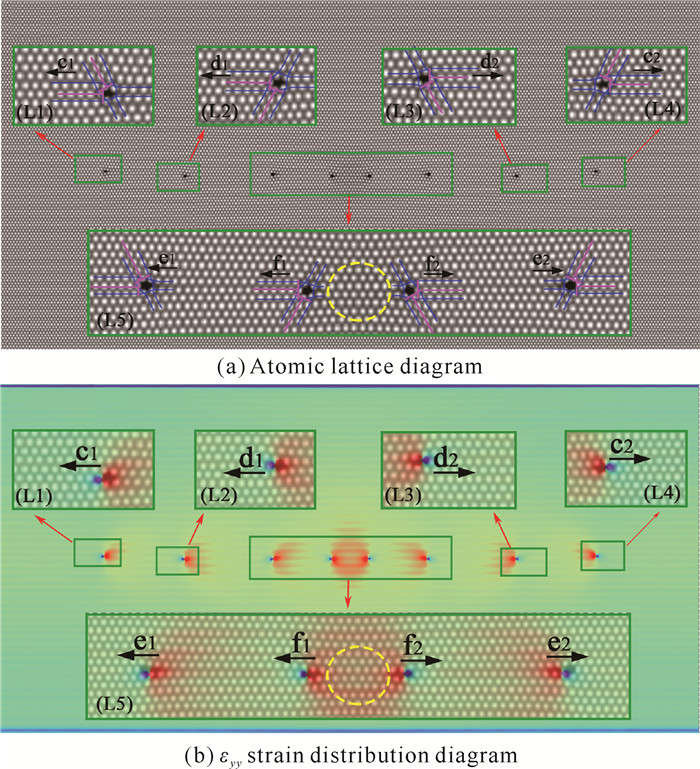
由图 10中插图(K7)和(K8)可见,缺口附近发射f1和f2位错对,修复了孔洞的第6层原子面;而孔洞最后一层原子面的修复不依靠位错发射完成,而是由其他平面的原子逐渐向缺口处迁移实现。发射位错对f1和f2所在区域受压应变作用,该原子面提前闭合,扩展驱动力下降,最后孔洞消失,裂纹修复完成。图 11表示到444 000步时,厚度为7层原子面的孔洞修复完成。由图 11(a)中插图(L5)可见,原孔洞所在虚线圆区域已愈合成完整的单晶。图 11(b)中有8处应力集中区域,与图 11(a)已经发射的位错对位置一致。
|
| 图 10 K点的样品演化图(n=435 500 ts) Fig. 10 Evolution diagram of the sample at point K (n=435 500 ts) |
|
| 图 11 L点的样品演化图(n=444 000 ts) Fig. 11 Evolution diagram of the sample at point L (n=444 000 ts) |
3 结论
裂纹孔洞愈合过程分为3个阶段:缺口两侧局部凸起发生孔洞扩展与位错的产生、位错发射导致缺口厚度的台阶数减少、缺口区域的消失。位错发射机制是孔洞愈合的主要表现形式,当样品缺口厚度大于2层原子面时,缺口两侧会同时发射位错以实现孔洞缩口,最后1层原子面的修复会以其他平面原子迁移填充的方式进行。当压应变达到临界应力条件时,凸口会发射位错,并出现几个格点大小的应力集中区域,该区域的位置会随着位错运动而移动。
| [1] |
ANDO K, TAKAHASHI K, NAKAO W, et al. New technology for increasing through-life reliability of ceramics components using self-crack-healing ability[J]. Journal of Powder Technology, 2013, 2013: 1-11. |
| [2] |
NIU J H, JIN H, MENG S H, et al. ZrO2-induced crack-healing mechanism of ZrB2-SiC-Graphite composite in high temperature atomic oxygen environment[J]. Ceramics International, 2016, 42(4): 5562-5568. DOI:10.1016/j.ceramint.2015.12.031 |
| [3] |
冯铁程. 氧化物陶瓷宏观裂纹的修复[D]. 天津: 天津大学, 2005.
|
| [4] |
PLAISTED T A, NEMAT-NASSER S. Quantitative evaluation of fracture, healing and re-healing of a reversibly cross-linked polymer[J]. Acta Materialia, 2007, 55(17): 5684-5696. DOI:10.1016/j.actamat.2007.06.019 |
| [5] |
HAN J Q, DING Q Q, MEI C T, et al. An intrinsically self-healing and biocompatible electroconductive hydrogel based on nano structured nanocellulose-polyaniline complexes embedded in a viscoelastic polymer network towards flexible conductors and electrodes[J]. Electrochimica Acta, 2019, 318: 660-672. DOI:10.1016/j.electacta.2019.06.132 |
| [6] |
WOOD E L, SANSOZ F. Growth and properties of coherent twinning superlattice nanowires[J]. Nanoscale, 2012, 4(17): 5268-5276. DOI:10.1039/c2nr31277h |
| [7] |
ZHANG R B, YE C S, ZHANG Y Y. Strengthening of porous TiB2-SiC ceramics by pre-oxidation and crack-healing[J]. Applied Surface Science, 2016, 360(Part B): 1036-1040. |
| [8] |
NAKAHATA M, TAKASHIMA Y, YAMAGUCHI H, et al. Redox-responsive self-healing materials formed from host-guest polymers[J]. Nature Communications, 2011, 2(1): 511. DOI:10.1038/ncomms1521 |
| [9] |
KUMAR A, PAUL S K. Healing of fatigue crack in steel with the application of pulsed electric current[J]. Materialia, 2020, 14: 100906. DOI:10.1016/j.mtla.2020.100906 |
| [10] |
CHEN Z Q, JI L G, GUO N S, et al. Crack healing and strength recovery of Al2O3/TiC/TiB2 ceramic tool materials[J]. International Journal of Refractory Metals and Hard Materials, 2020, 87: 105167. DOI:10.1016/j.ijrmhm.2019.105167 |
| [11] |
LI J, FANG Q H, LIU B, et al. Mechanism of crack healing at room temperature revealed by atomistic simulations[J]. Acta Materialia, 2015, 95: 291-301. DOI:10.1016/j.actamat.2015.06.006 |
| [12] |
LI M, CHU W Y, GAO K W, et al. Molecular dynamics simulation of healing of an ellipsoid crack in copper under compressive stress[J]. Materials Letters, 2004, 58(5): 543-546. DOI:10.1016/j.matlet.2003.06.016 |
| [13] |
XU G Q, DEMKOWICZ M J. Healing of nanocracks by disclinations[J]. Physical Review Letters, 2013, 111(14): 145501. DOI:10.1103/PhysRevLett.111.145501 |
| [14] |
QI Y, KRAJEWSKI P E. Molecular dynamics simulations of grain boundary sliding: the effect of stress and boundary misorientation[J]. Acta Materialia, 2007, 55(5): 1555-1563. DOI:10.1016/j.actamat.2006.10.016 |
| [15] |
吴兴惠, 项金钟. 现代材料计算与设计教程[M]. 北京: 电子工业出版社, 2002.
|
| [16] |
CAO Z H, WANG L, HU K, et al. Microstructural evolution and its influence on creep and stress relaxation in nanocrystalline Ni[J]. Acta Materialia, 2012, 60(19): 6742-6754. DOI:10.1016/j.actamat.2012.08.047 |
| [17] |
ELDER K R, KATAKOWSKI M, HAATAJA M, et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88(24): 245701. DOI:10.1103/PhysRevLett.88.245701 |
| [18] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70(5): 051605. DOI:10.1103/PhysRevE.70.051605 |
| [19] |
ELDER K R, ROSSI G, KANERVA P, et al. Patterning of heteroepitaxial overlayers from nano to micron scales[J]. Physical Review Letters, 2012, 108(22): 226102. DOI:10.1103/PhysRevLett.108.226102 |
| [20] |
GAO Y J, HUANG L L, DENG Q Q, et al. Simulation of epitaxial growth on convex substrate using phase field crystal method[J]. Frontiers of Materials Science, 2014, 8(2): 185-192. DOI:10.1007/s11706-014-0243-y |
| [21] |
LI Y X, GAO Y J, YI X A, et al. Phase field crystal simulation of gap healing at nanoscale[J]. Modelling and Simulation in Materials Science and Engineering, 2022, 30(6): 064004. DOI:10.1088/1361-651X/ac8174 |
| [22] |
GREENWOOD M, ROTTLER J, PROVATAS N. Phase-field-crystal methodology for modeling of structural transformations[J]. Physical Review E, 2011, 83(3): 031601. |
| [23] |
MKHONTA S K, ELDER K R, HUANG Z F. Exploring the complex world of two-dimensional ordering with three modes[J]. Physical Review Letters, 2013, 111(3): 035501. DOI:10.1103/PhysRevLett.111.035501 |
| [24] |
HUANG L L, GAO Y J, DENG Q Q, et al. A study of relationship between dislocation configuration of nanocrack and brittle-ductile mode of fracture: atomistic modeling[J]. Computational Materials Science, 2020, 173: 109413. DOI:10.1016/j.commatsci.2019.109413 |
| [25] |
LIU Z Y, GAO Y J, DENG Q Q, et al. A nanoscale study of nucleation and propagation of Zener types cracks at dislocations: phase field crystal model[J]. Computational Materials Science, 2020, 179: 109640. DOI:10.1016/j.commatsci.2020.109640 |
| [26] |
GAO Y J, DENG Q Q, HUANG L L, et al. Atomistic modeling for mechanism of crack cleavage extension on nano-scale[J]. Computational Materials Science, 2017, 130: 64-75. DOI:10.1016/j.commatsci.2017.01.003 |
| [27] |
邓力滔, 卢昱江, 刘哲源, 等. 晶体相场法模拟晶界萌生裂纹扩展机理[J]. 广西科学, 2018, 25(6): 658-662. DOI:10.13656/j.cnki.gxkx.20181225.002 |
| [28] |
周文权, 黄世叶, 王震, 等. 高温应变作用下小角度晶界湮没过程的晶体相场模拟[J]. 广西科学, 2014, 21(3): 247-251. DOI:10.13656/j.cnki.gxkx.20140504.005 |
| [29] |
叶里, 胡绪志, 黄礼琳, 等. 拉应力作用下晶界位错运动过程的晶体相场模拟[J]. 广西科学, 2016, 23(5): 470-473, 484. |
| [30] |
WU K A, VOORHEES P W. Phase field crystal simulations of nanocrystalline grain growth in two dimensions[J]. Acta Materialia, 2012, 60(1): 407-419. DOI:10.1016/j.actamat.2011.09.035 |
| [31] |
CHEN L Q, SHEN J. Applications of semi-implicit Fourier-spectral method to phase field equations[J]. Computer Physics Communications, 1998, 108(2/3): 147-158. |



