金属材料内部存在大量晶界,晶界的运动与晶体自身的缺陷对材料性能起决定性作用[1]。晶界往往是决定高温塑性性质的主导因素[2]。在纳米晶体材料中,随着晶界密度的增加,晶界对力学行为的影响就越显著[1-8]。晶界特性与温度密切相关,高温时晶界会出现预熔化现象[9]。晶界预熔化现象是由晶界的熔点低于完整晶粒的熔点引起的。1948年,Chaudron等[10]首次用电镜观测到材料的晶界预熔化现象。1997年,在0.5 Tm(熔点温度)下,Inoko等[11]首次发现了铜薄膜的双晶晶界上出现外部应力诱发预熔化的现象。2005年,Alsayed等[12]用显微镜观察到晶界和大块胶体晶体中的预熔化现象。2022年,Xiao等[13]用聚焦光束局部加热大块硬球胶体晶体中的单个晶界,并用电镜观察单晶界的预熔化过程。由于实验观测的局限性,研究者开始通过原子点阵变化的计算和模拟来探究材料微观结构的演化。例如,Yang等[14]结合改进的遗传算法、混合型蒙特卡罗方法和分子动力学来模拟晶界的预熔化。Bhogireddy等[15]利用障碍势进行晶界预熔化的相场建模。Fensin等[16]利用分子动力学建模探究晶界预熔化和晶粒聚结的结合作用。此外,晶体相场(PFC)法也可研究高温晶界预熔化现象,该方法具有原子级别的分辨能力,其不仅在材料纳米裂纹的微观缺陷上有着广泛的运用,而且也能深入研究晶界预熔化现象[17-21]。
Robbins等[19]应用晶体相场法探究晶界预熔化行为时发现,大角晶界排斥和小角晶界吸引存在定性的差异。Berry等[17]发现在低角度晶界的熔化过程中,每个位错核径向熔化,直至相邻位错的熔化区域合并,该熔化区沿晶界形成均匀的润湿层。Mellenthin等[22]发现晶界预熔化区域发生从单个位错到位错对的滞后结构转变,预熔化区以“池”的形式出现在位错周围,没有均匀的液体膜。此外,随着熔点的接近,晶界结构发生转变,出现位错配对,即两个位错连接并被一个共同的液池包围。预熔化对晶界性能的影响已经被广泛讨论[23],其中包括晶界扩散速率的增强和晶界位错剪切阻力的显著降低。目前,配对的位错预熔化区域在受到应变作用时的结构变化已引起人们的广泛关注。Gao所在课题组[24-27]采用晶体相场模型研究了在应力作用下,对称倾侧小角晶界位错的预熔化区域内位错对的萌生增殖、滑移、交滑移、湮没等现象。本研究在施加双轴加载应变的条件下,观察高温晶界预熔化区的位错配对,研究高温预熔化条件下位错芯的扩展、位错增殖以及湮没等现象,拟揭示高温晶界的位错结构的转变特性。
1 模型与方法 1.1 PFC模型PFC模型采用周期性的局部原子密度φ作为序参量。在晶体相中,局部原子密度φ具有周期性特征;在液相中,φ为常数。在液-固系统中无量纲纯物质的自由能F[28]可构造为
| $ F=\int\left\{\frac{\varphi}{2}\left[\gamma+\left(\nabla^2+1\right)^2\right] \varphi+\frac{1}{4} \varphi^4\right\} \mathrm{d} r, $ | (1) |
式中,φ为原子密度,参数γ表征体系的温度参数,
控制体系演化的无量纲动力学方程[29]为
| $ \frac{\partial \varphi}{\partial t}=\nabla^2\left(\frac{\delta F}{\delta \varphi}\right)=\nabla^2\left\{\left[r+\left(\nabla^2+1\right)^2\right] \varphi+\varphi^3\right\} 。$ | (2) |
公式(2)的二维三角晶相φ的单模近似解为
| $ \begin{aligned} & \quad \varphi=A_T[\cos (q x) \cos (q y / \sqrt{3})-\cos (2 q y / \sqrt{3}) / \\ & 2]+\varphi_0, \end{aligned} $ | (3) |
式中, x、y为空间坐标,φ0为平均密度,波数
为简明起见,本研究体系设置为二维双晶体系,设置样品的尺度区域为Lx×Ly=512Δx×512Δy正方形,满足周期边界条件。将样品区域分为3个矩形区域:0 < x < Lx/4,Lx/4 < x < 3Lx/4,3Lx/4 < x < Lx。基于公式(3),在0 < x < Lx/4和3Lx/4 < x < Lx区域范围内,设置取向角θ= 2°(θ为三角相原子面与y轴的夹角)的三角晶相结构;在Lx/4 < x < 3Lx/4范围内,设置取向角θ=-2°的三角晶相结构,最后通过计算得到单相双晶的晶界取向差为4°。
样品制备过程分为两个阶段:第一阶段制备低温下的双晶样品,该样品制备的参数值为γ=-0.3,φ0=-0.199,体系弛豫时间步长为5 000步;第二阶段制备高温下的双晶样品,所选取的参数为γ=-0.1,φ0=-0.199,体系弛豫时间步长为105步,直至体系达到热平衡状态。
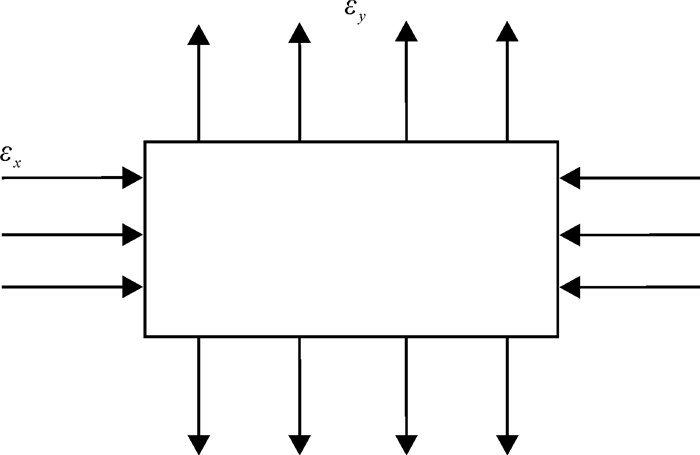
在本研究的PFC变形模拟过程中,施加拉压双轴应变作用于制备好的预熔化样品,示意图如图 1所示。变形采用等面积条件假设[30, 31],设
|
| 图 1 对样品施加双轴拉压加载应变的示意图 Fig. 1 Schematic diagram of biaxial loading applied to the sample |
| $ S=\Delta x \Delta y=\Delta x^{\prime} \Delta y^{\prime}, $ | (4) |
式中,Δx和Δy为初始空间步长,Δx′和Δy′为变形后的空间步长,应变加载沿y轴方向拉伸,经过n个时间步长后,空间步长采用公式(5)进行运算[25]:
| $ \Delta x^{\prime}=\Delta x /(1+n \dot{\varepsilon} \Delta t), \Delta y^{\prime}=\Delta y(1+n \dot{\varepsilon} \Delta t), $ | (5) |
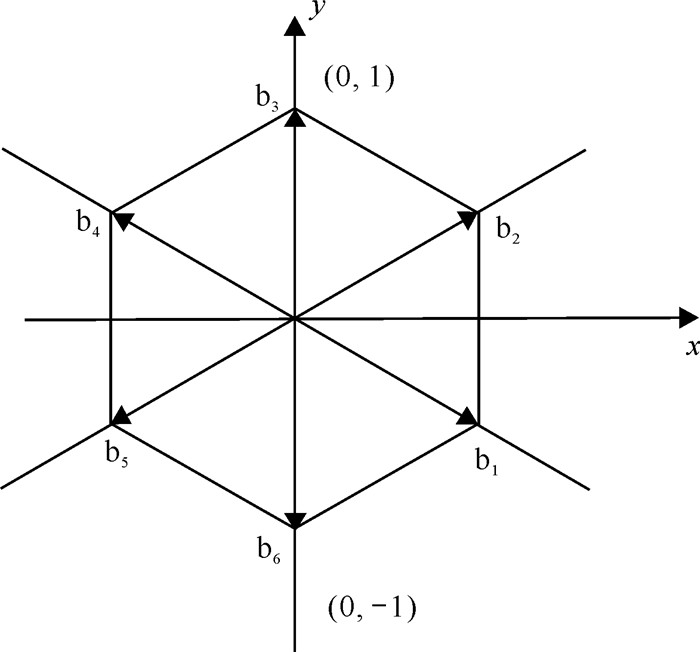
即可得到拉压加载的应变效果。为了表示加载应变过程的位错Burgers矢量的变化,图 2给出了6种可能的位错Burgers矢量方向。
|
| 图 2 二维六角晶格可能的Burgers方向 Fig. 2 Possible Burgers direction of two-dimensional hexagonal lattice |
2 结果与分析 2.1 样品晶界位错预熔化结构
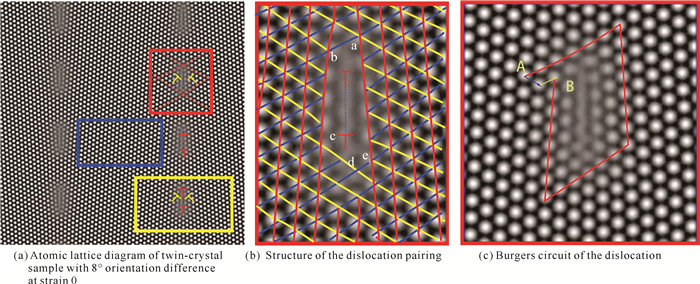
图 3(a)为用PFC模拟得到的样品高温晶界位错预熔化结构。由该图可见,在样品的一条晶界上,有4个棒状的预熔化区域,2条晶界共8个预熔化区域。每个预熔化区域内的位错组态由上下位错配对和两侧位错配对的扩展位错组成,如黄色矩形框图中的位错结构所示。在图 3(a)中,红色方框区域给出黄色配对位错,同样在预熔化区域内也出现上下配对的红色位错(此处没有标出),这种上下配对的位错之间存在一层错区域,该层错区域的细节如图 3(b)和(c)所示,它是由两侧的扩展位错的重叠区域产生,从而构成复合扩展位错团(由4个位错组合)的芯结构,如图 3(a)黄色方框所示。
|
| 图 3 高温晶界位错预熔化结构 Fig. 3 Structure of dislocation premelting in grain boundary at high temperature |
图 3(b)给出高温晶界位错预熔化区域的原子点阵放大细节图。预熔化区域是关于y轴对称的结构。晶列在位错芯区域发生折断、不连续,其中位错芯区域的底部明显多出了两列原子列,相当于预熔化区域的晶体点阵多出了两个半原子面(线),而位错芯的左右两侧的原子排列也发生了折断、不连续。例如,穿出位错芯两侧的蓝色晶列线在位错芯区域发生折断、不连续,左边有5条蓝色晶列线进入预熔化位错芯区域,而从位错芯右边出来的蓝色晶列线变成了4条,少了一条原子晶列,说明该预熔化区域是位错的源。由于是5/4比例,说明该方向的位错是扩展型的。同样,从预熔化位错芯区域左侧进入的黄色晶列线为4条,而从右侧出来的黄色晶列线有5条,多了一条晶列,说明该方向区域存在4/5比例的位错扩展状态。从蓝色和黄色的晶列方向看,预熔化区域是一个扩展的位错芯结构,左右各有4-5个原子距离的宽度。该宽度的区域可看作是扩展位错的广义层错区。这个扩展的位错芯区域把左右排列的一对不全位错紧密地拴连在一起,构成了一个复杂的二维扩展位错团结构,Gao等[24]和高英俊等[32]研究也发现有相似的结构。
图 3(c)给出了配对位错预熔化区域的Burgers矢量回路图,该图中的连接端点为A和B,说明配对位错预熔化区域存在两个单位的柏氏矢量b1和b2,分别用蓝色和黄色的箭头表示。由图 2可知,
对样品施加x轴和y轴方向的双轴应变,其中x轴方向为压应变,y轴方向为拉应变,观察在此双轴拉压应变作用下,预熔化区的复合位错团结构随应变增加的演化规律。图 3(a)中红色方框和黄色矩形框内部预熔化区域的原子晶格演化规律是一样的。但为了研究需要,红色方框区域的晶格结构演化主要用于展示预熔化区域初始阶段的演化细节;而黄色矩阵框区域主要用于展示在施加应变的后期,预熔化区配对位错结构的扩展、位错增殖和分离的细节过程,揭示其中的演化规律。
2.2.1 预熔化区的横向扩展如图 4(a)和(b)所示,在双轴加载的正应变条件下,当ε=0.016 5和0.024 0时,图 3(b)中的预熔化区域abcdea发生了明显的变化,由棒状的五边形变成了对称的钟型六边形abcdefa,其上部窄、下部宽且关于y轴对称。由上往下看,只有一条红色的晶列进入预熔化区域abcdefa,且在该区域折断,但从预熔化区域的底部出来却是3条红色的晶列线,即增加了两条,表明该预熔化区域是竖直方向的两个刃型位错的源。如图 4(c)所示,当正应变增加到ε=0.030 0时,图 4(b)中预熔化区的形状发生明显变化,从钟型的六边形变成了扁的六边形,预熔化区明显变宽。由上往下看,原来有3条红色的晶列线从上部进入到预熔化区域,从下部出来5条红色的晶列线[图 4(c)]。由图 4(d)可见,从上部进入预熔化区域的红色晶列线变成了7条,从下部出来的红色晶列线变成了9条,而且预熔化区明显变宽,正六边形的预熔化区向菱形状转变。因此,预熔化区域从初始的棒状结构变成六边形再变为菱形,但区域的面积增加。预熔化区域内的原子点阵排列较为复杂,是产生新位错的源头。如图 4(d)所示,当双轴加载的正应变(ε)增大,上下排列的一对位错横向扩展,变成平行并列排列,六边形预熔化区内有晶列特征;而六边形顶部区域b的原子晶格出现了较为有序的点阵排列特征,表明原来在顶角b点的上端位错已发生转移,与原来下部的位错形成并排的扩展位错。由图 4(d)可见,原图 3(b)中预熔化区域的侧向晶列穿过预熔化区域的特征基本保持不变,即进入预熔化区域的蓝色和黄色晶列数为5条,而离开该预熔化区域的晶列数则变为6条。如果将初始的预熔化区域看作预熔化带,那么现在为预熔化面结构,由一维扩展成了二维结构。
2.2.2 预熔化区扩展与位错萌生
由图 5(a)可见,当应变ε=0.042时,预熔化区域进一步扩展,区域呈菱形。在竖直方向范围,从上部垂直进入预熔化区域的红色晶列有11条,从下部出来的红色晶列有13条,二者相差两条,说明预熔化区域沿横向发生扩展,位错芯变宽,达到13个原子的距离。两侧的蓝色和黄色晶列,进入预熔化区域的数目为6条,出来的晶列数为7条,比图 3(b)中区域变宽,表明预熔化区域位错芯内的原子排列有序度降低。在菱形预熔化区的位错芯,上部的原子排列显现出较好的周期性结构,而菱形区域两侧和底部的原子晶列排列模糊、有序度较低,这些区域是新位错萌生的源头。这种二维预熔化区域可以看作是复杂的扩展位错的位错芯或者面积层错(广义的)。由图 5(a)清晰可见,晶列滑移沿蓝色和黄色的晶列方向,指向菱形两侧的顶角方向。
如图 5(b)所示,随着应变增大到ε=0.045时,预熔化区域的菱形形状进一步扩大,菱形的边长为7-8个原子的宽度,而菱形的横向扩展达到15个原子的宽度;从上部进入到预熔化区域的红色晶列线有14条,从下部出来的红色晶列线有16条。此外,预熔化区域的上部顶角区域的原子晶格排列较为整齐,有序度较高,而菱形区域两侧顶角区域的有序度较低,预熔化区域形状呈现出“V”形,并且向“V”形进一步发展。由图 5(c)可见,预熔化区域的“V”形更加扩展,横向达到20个原子的宽度。因此,预熔化的宽度进一步扩大,而预熔化区域内形成了两个带状的子预熔化区域,构成了“V”形的两个翼。由图 5(c)可见,ab-f端和de-f端的预熔化带状区域存在位错结构,因此在扩展位错预熔化区域“V”形的端点处萌生了一对新位错,详见图中绿色的位错符号。图 5(c)显示位错芯沿3个方向扩展,预熔化区呈现显著的“V”形。这时由于预熔化区域横向扩展,原上下排列的一对位错转变为左右并行排列的扩展位错,而在两端ab和de萌生出一对新位错,准备脱离预熔化区。
由图 5(d)可见,在“V”形预熔化区两侧发生位错发射时,“V”形预熔化区的扩展位错横向收缩,宽度由图 5(c)的20个原子宽度收缩为9个原子宽度。如图 5(e)所示,由于向外发射位错,使得预熔化扩展的区域收缩,由“V”形又转变为近似的正六边形,该六边形预熔化区为扩展位错芯,内部晶格有序度下降,转为混乱,同时伴随着位错芯结构的转变。由蓝色框放大图 5(f)可见,不同预熔化区发射的位错传播相互靠近,即将发生湮没。
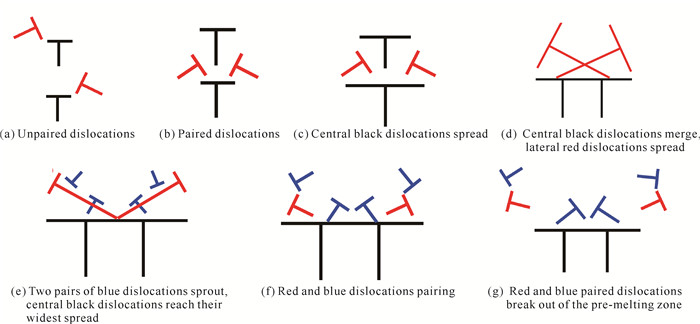
2.2.3 预熔化区的位错组态转变如图 6所示,预熔化晶界位错组态演化过程可归纳为几个步骤。低温小角度对称倾侧晶界上,位错对不发生聚集,孤立排列[图 6(a)];高温晶界的位错发生聚集配对,由4个位错组合成位错团结构[图 6(b)];随后位错团发生了明显的扩展和变化,两个上下排列的位错(黑色位错)经过横向扩展,发生并合,而红色位错在滑移的同时进行扩展并相互交换位置[图 6(c)和(d)];在预熔化区域,位错团向两侧继续扩展,在红色位错附近,萌生出一对新的蓝色位错[图 6(e)]。此时,位错团由8个位错组成,增殖了4个位错。萌生的新位错对经过滑移,其中的一个孤立位错分别与红色的孤立位错进行配对,而剩下的两个新生孤立位错(蓝色位错)同样进行配对[图 6(f)];最后,在扩展位错的头部发生了位错对的发射和传播[图 6(g)]。
|
| In the figure, the black symbol represents a central dislocation, the red symbol represents a lateral dislocation, and the blue symbol represents a new dislocation.An elongated dislocation symbol indicates that the dislocation core is extended. 图 6 预熔化区的位错组态演化示意图 Fig. 6 A schematic diagram of dislocation configuration evolution in the pre-melting region |
3 结论
本研究采用晶体相场方法探究在双轴加载的拉压应变条件下,高温配对位错预熔化区域的形状变化及内部位错组态的演化过程,认为高温下配对位错的预熔化区呈棒状,其内部包含4个位错组成的位错团,具有纵向对称结构。其中一对位错上下排列,另一对出现在该位错对的左右两侧的肩膀上,位错芯的原子排列模糊不规则。施加应变作用后,位错团开始横向扩展,上下一对位错靠近并转变成为并列平行的位错对,位错团两侧肩膀的位错也发生侧向扩展。预熔化区由开始的棒状转变为近似六边形,然后变为菱形。随着应变进一步的增大,预熔化区由菱形转变为“V”形。在“V”形的预熔化区两端,萌生出一对位错,此时位错团的组态转变为3组配对的位错,预熔化区横向扩展达到最宽。随后,“V”形的预熔化区两端发射位错并开始收缩,又由“V”形转变为六边形,最后又恢复到原来棒状的位错团结构。上述分析说明,预熔化区内部原子晶格较软,原子位错振动强烈且容易发生晶列滑动,引起局部滑移,导致预熔化区扩展,萌生新的位错。
| [1] |
UPMANYU, SROLOVITZ D J, LOBKOVSKY A E, et al. Simultaneous grain boundary migration and grain rotation[J]. Acta Materialia, 2006, 54(7): 1707-1719. DOI:10.1016/j.actamat.2005.11.036 |
| [2] |
LANGDON T G, WATANABE T, WADSWORTH J. Future research directions for interface engineering in high temperature plasticity[J]. Materials Science and Engineering: A, 1993, 166(1/2): 237-241. |
| [3] |
QIN R S, WALLACH E R. A phase-field model coupled with a thermodynamic database[J]. Acta Materialia, 2003, 51(20): 6199-6210. DOI:10.1016/S1359-6454(03)00443-9 |
| [4] |
SCHIØTZ J, VEGGE T. Computer simulations of the mechanical properties of metals[J]. Science Progress, 1999, 82(4): 313-325. DOI:10.1177/003685049908200403 |
| [5] |
CANTWELL P R, MING T, DILLON S J, et al. Grain boundary complexions[J]. Acta Materialia, 2014, 62(1): 1-48. |
| [6] |
HAN J, VITEK V, SROLOVITZ D J. Grain-boundary metastability and its statistical properties[J]. Acta Materialia, 2016, 104: 259-273. DOI:10.1016/j.actamat.2015.11.035 |
| [7] |
ELDER K R, KATAKOWSKI M, HAATAJA M, et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88(24): 245701. DOI:10.1103/PhysRevLett.88.245701 |
| [8] |
CAI X C, LIANG J J, XU L D, et al. Ultrastrong nanocrystalline oxide-dispersion-strengthened ferritic alloy with exceptional thermal stability[J]. Materials Science and Engineering: A, 2021, 821: 141616. DOI:10.1016/j.msea.2021.141616 |
| [9] |
DIVINSKI S, LOHMANN M, HERZIG C, et al. Grain boundary melting phase transition in the Cu-Bi system[J]. Physical Review B, 2005, 71(10): 104104. DOI:10.1103/PhysRevB.71.104104 |
| [10] |
CHAUDRON G, LACOMBE P, YANNAQUIS N. Intergranular corrosion of pure aluminium in relation to the behavior of grain-boundaries during melting[J]. Nature, 1948, 162(4126): 854-855. |
| [11] |
INOKO F, HAMA T, TAGAMI M, et al. Grain boundary premelting in thin foils of deformed copper bicrystals[J]. Ultramicroscopy, 1991, 39(1/2/3/4): 118-127. |
| [12] |
ALSAYED A M, ISLAM M F, ZHANG J, et al. Premelting at defects within bulk colloidal crystals[J]. Science, 2005, 309(5738): 1207-1210. DOI:10.1126/science.1112399 |
| [13] |
XIAO X M, WANG L L, WANG Z J, et al. Superheating of grain boundaries within bulk colloidal crystals[J]. Nature Communications, 2022, 13(1): 1599. DOI:10.1038/s41467-022-29254-z |
| [14] |
YANG S F, ZHOU N X, ZHENG H, et al. First-order interfacial transformations with a critical point: breaking the symmetry at a symmetric tilt grain boundary[J]. Physical Review Letters, 2018, 120(8): 085702. DOI:10.1103/PhysRevLett.120.085702 |
| [15] |
BHOGIREDDY V S P K, HVTER C, NEUGEBAUER J, et al. Phase-field modeling of grain-boundary premelting using obstacle potentials[J]. Physical Review E, 2014, 90(1): 012401. DOI:10.1103/PhysRevE.90.012401 |
| [16] |
FENSIN S J, OLMSTED D, BUTA D, et al. Structural disjoining potential for grain-boundary premelting and grain coalescence from molecular-dynamics simulations[J]. Physical Review E, 2010, 81(3): 031601. |
| [17] |
BERRY J, ELDER K R, GRANT M. Melting at dislocations and grain boundaries: a phase field crystal study[J]. Physical Review B, 2008, 77(22): 224114. DOI:10.1103/PhysRevB.77.224114 |
| [18] |
TIAN X L, ZHAO Y H, PENG D W. Phase-field crystal simulation of evolution of liquid pools in grain boundary pre-melting regions[J]. Transactions of Nonferrous Metals Society of China, 2021, 31(4): 1175-1188. DOI:10.1016/S1003-6326(21)65570-X |
| [19] |
ROBBINS M J, ARCHER A J, THIELE U, et al. Modeling the structure of liquids and crystals using one- and two-component modified phase-field crystal models[J]. Physical Review A, 2012, 85(6): 061408. |
| [20] |
LU Y L, HU T T, LU G M, et al. Phase-field crystal study of segregation induced grain-boundary premelting in binary alloys[J]. Physica B: Condensed Matter, 2014, 451: 128-133. DOI:10.1016/j.physb.2014.06.037 |
| [21] |
ADLAND, KARMA A, SPATSCHEK R, et al. Phase-field-crystal study of grain boundary premelting and shearing in bcc iron[J]. Physical Review B, 2013, 87(2): 024110. DOI:10.1103/PhysRevB.87.024110 |
| [22] |
MELLENTHIN J, KARMA A, PLAPP M. Phase-field crystal study of grain-boundary premelting[J]. Physical Review B, 2008, 78(18): 184110. DOI:10.1103/PhysRevB.78.184110 |
| [23] |
OLMSTED D L, BUTA D, ADLAND A, et al. Dislocation-pairing transitions in hot grain boundaries[J]. Physical Review Letter, 2011, 106(4): 046101. DOI:10.1103/PhysRevLett.106.046101 |
| [24] |
GAO Y J, HUANG L L, DENG Q Q, et al. Phase field crystal simulation of dislocation configuration evolution in dynamic recovery in two dimensions[J]. Acta Materialia, 2016, 117: 238-251. DOI:10.1016/j.actamat.2016.06.021 |
| [25] |
GAO Y J, DENG Q Q, LIU Z Y, et al. Modes of Grain growth and mechanism of dislocation reaction under applied biaxial strain: atomistic and continuum modeling[J]. Journal of Materials Science & Technology, 2020, 49: 236-250. |
| [26] |
刘哲源, 卢昱江, 李依轩, 等. 高温应变下的晶界位错结构组态演化的晶体相场模拟[J]. 广西科学院学报, 2018, 34(4): 292-297, 303. |
| [27] |
黄礼琳, 邓芊芊, 卢昱江, 等. 缺陷预熔化现象的晶体相场模拟[J]. 广西科学院学报, 2017, 33(4): 234-239. |
| [28] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2005, 70(5): 051605. |
| [29] |
STEFANOVIC P, HAATAJA M, PROVATAS N. Phase field crystal study of deformation and plasticity in nanocrystalline materials[J]. Physical Review E, 2009, 80(4): 046107. DOI:10.1103/PhysRevE.80.046107 |
| [30] |
TAKAKI T, TOMITA Y. Static recrystallization simulations starting from predicted deformation microstructure by coupling multi-phase-field method and finite element method based on crystal plasticity[J]. International Journal of Mechanical Sciences, 2010, 52(2): 320-328. DOI:10.1016/j.ijmecsci.2009.09.037 |
| [31] |
HIROUCHI T, TAKAKI T, TOMITA Y. Development of numerical scheme for phase field crystal deformation simulation[J]. Computational: Materials Science, 2009, 44(4): 1192-1197. DOI:10.1016/j.commatsci.2008.08.001 |
| [32] |
高英俊, 卢昱江, 孔令一, 等. 晶体相场模型及其在材料微结构演化中的应用[J]. 金属学报, 2018, 54: 278-292. |





