2. 华南师范大学数据科学与工程学院,广东汕尾 516600;
3. 华南师范大学商学院,广东汕尾 516600
2. School of Data Science & Engineering, South China Normal University, Shanwei, Guangdong, 516600, China;
3. School of Business, South China Normal University, Shanwei, Guangdong, 516600, China
现实中存在大量需要同时优化多个目标的优化问题,即多目标优化问题(Multi-objective Optimization Problem,MOP)。由于MOP中各目标间通常相互冲突,因此一般并不存在唯一解,通常是一组折中解,即Pareto解集或非劣解集[1]。基于群体搜索的进化算法(Evolutionary Algorithm,EA)运行一次即可获得一组解,且对待解问题的数学性质不做特别要求,因而适于求解MOP。近30多年来,已出现数目众多的多目标进化算法(Multi-Objective Evolutionary Algorithm,MOEA),这些MOEA在求解两至三个目标的MOP时通常具有较好的性能,得到了广泛应用[2]。
但随着经济社会的发展,现实中不断涌现出要求同时优化更多目标的问题[3, 4],即高维多目标优化问题(Many-objective Optimization Problems,MaOPs)。MaOP通常含有4个及以上数目的目标函数,其固有的高维目标空间特性会显著地恶化基于Pareto支配的MOEA性能[5]。究其原因:其一,有限规模的种群中非支配解的占比随目标数目呈指数级增长,严重削弱了利用Pareto支配进行选择的压力,将导致算法最终退化成完全随机算法;其二,高维目标种群极易产生支配抵触解(Dominance Resistance Solutions,DRSs),而DRSs是一些远离Pareto前沿的非支配解,它们会显著地恶化算法的收敛性;其三,当Pareto占优无法区分解个体优劣时,一些MOEA会利用辅助的基于密度的方法择优个体,亦即采用主动多样性促进(Active Diversity Promotion, ADP)机制进行环境选择。因此,在DRSs和ADP共同作用下,这些MOEA获得的近似解集难以收敛到待解问题真实的Pareto前沿上。由此可知,大量存在的MaOP给传统的MOEA带来了严峻挑战,迫切需要发展高维多目标进化算法(Many-Objective Evolutionary Algorithm,MaOEA), 以有效求解各种MaOP。
迄今为止,国内外研究者基于不同的研究背景和视角提出了多种MaOEA,可将它们粗略地分成以下2种类型。
① 基于改进支配关系的方法。由于传统的Pareto占优是一种颇为严格的支配关系,其在高维目标空间可扩展性差。为有效求解MaOP,研究者提出了若干改进的支配方法以改善算法求解MaOP的性能。例如:修改个体目标函数值方法[6]、目标计数方法[7]、改进Pareto最优性的方法[8]、利用角度的方法[9]以及利用小生境的方法[10]等。这些方法在收敛性和多样性方面各有侧重,难以兼顾并平衡二者。然而,在高维多目标优化中有效地平衡种群的收敛性和多样性至关重要,其在相当程度上决定了算法解题的效率与效果。另外,这些支配方法大都需要设置合适参数,且算法性能通常对参数敏感,因而不便于使用。
② 基于参考点或参考向量的方法。这类方法通过在目标空间生成均匀分布的参考点或参考向量引导种群个体的进化,以期获得收敛性和多样性均优的解群。这里以经典的NSGA-Ⅱ[11]和NSGA-Ⅲ[12]算法为例,早期的NSGA-Ⅱ利用Pareto支配和拥挤距离择优个体,其在低维目标空间可获得收敛性和多样性均较好的种群。但随着目标数目的增多,算法的性能明显恶化。为有效求解MaOP,NSGA-Ⅲ通过在高维目标空间预先定义一组均匀分布的参考点,利用参考点(参考向量)形成小生境,然后在小生境内选择性能较好的个体。利用参考点或参考向量(权重向量)引导种群进化的思想在算法REVA[13]和MOEA/DD[14]中亦有所体现。但这些基于参考点或参考向量的算法在进化过程中并未对解个体的收敛性和多样性进行动态调整,而适时调整种群个体的进化方向十分必要,其原因在于:在进化初期种群个体一般随机产生,它们的收敛性和多样性通常较差,因此早中期阶段的重点是促使种群朝Pareto前沿方向逼近;而后期由于种群已接近Pareto前沿,此时应强调种群多样性。不同的进化阶段实施不同的控制策略有利于获得高质量的解集。
基于此,为更有效地度量种群个体在进化过程中的收敛性和多样性以提高算法求解MaOP的性能,本文提出一种自适应地度量解个体收敛性与多样性的适应度指标(Fitness indicator considering convergence and diversity of individual adaptively,ICD)。ICD是一个标量值,因此通过直接比较不同个体的ICD值可判别出孰优孰劣,有效避免Pareto最优性易在高维目标空间出现大量非支配解而导致选择压力骤降的问题。为验证ICD的有效性,将其嵌入经典的NSGA-Ⅱ算法框架中[11],设计出一种基于ICD的高维多目标进化算法(Many-Objective Evolutionary Algorithm Based on ICD,MOEA/ICD)。相较于已有的高维多目标进化算法,MOEA/ICD算法主要特点包括: ①算法在迭代过程中可根据解个体所处阶段的不同,自适应地调整解个体的收敛性与多样性的占比,以较好地平衡高维多目标解群的收敛性和多样性,改善算法的总体性能; ②算法未额外引入参数,方便使用。
1 预备知识 1.1 多目标优化问题相关概念不失一般性,一个具有n个决策变量,m个目标函数的最小化MOP可形式化表示如下:
| $ \left\{\begin{array}{l} \min y=F(x)=\left(f_1(x), \cdots, f_m(x)\right)^{\mathrm{T}} \\ \text { s.t. } x \in \Omega \end{array}, \right. $ | (1) |
其中,m表示MOP的目标数目,x=(x1,x2,…,xn)是决策空间Ω中的点,
定义1:(Pareto支配)设x1, x2∈Ω是式(1)最小化MOP的任意两个解,称x1 Pareto支配x2(记为
定义2:(Pareto最优解)设x*∈Ω是Pareto最优解,当且仅当不存在其他解x∈Ω使得
定义3:(Pareto最优解集) Pareto最优解集(Pareto optimal Set,PS)是所有Pareto最优解的集合,即
定义4:(Pareto最优前沿)Pareto最优前沿(Pareto optimal Front,PF)是PS在目标空间中的投影,即
定义5:(理想点)理想点(ideal point)z*=(z1*, …, zm*)T是指式(1)最小化MOP所有的目标函数的解点,它的第i个分量zi*定义为
定义6:(最差点)最差点(nadir point)znad=(z1nad, …, zmnad)T由式(1)最小化MOP的PF上的最差值组成,它的第i个分量zinad定义为
通常,理想点z*和最差点znad界定了MOP解集在目标空间中的分布范围。
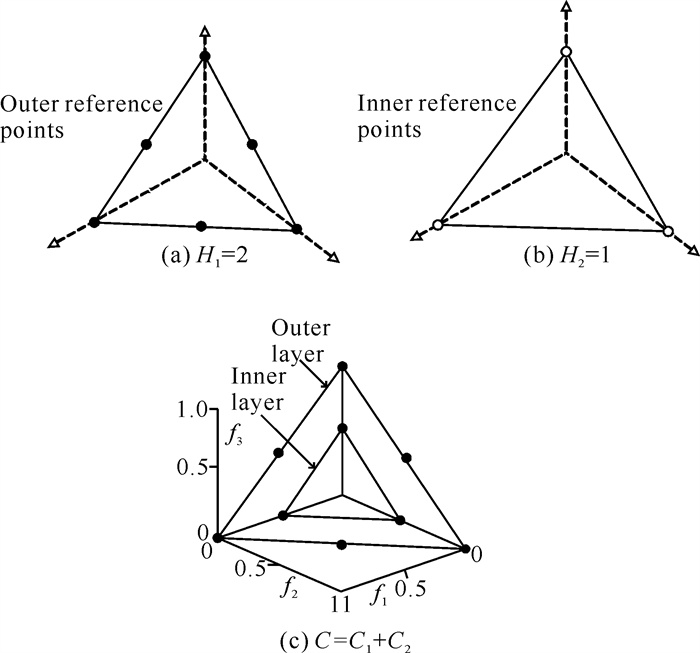
1.2 利用双层参考向量方法产生参考点在利用参考点(参考向量)方法求解MaOP时,如果采用Das等[15]提出的方法生成参考点容易导致过大的种群规模,会显著增加算法计算开销。这里利用Deb等[12]的双层参考向量方法生成参考点,每层参考点的数目按公式(2)计算:
| $ C=\left(\begin{array}{l} H+m-1 \\ m-1 \end{array}\right), $ | (2) |
其中C代表参考向量数目,m代表目标数量,H代表超平面上沿着每个目标方向考虑的划分等份。例如,对于一个3-目标优化问题,若在外层取H1=2,则外层参考向量数目为
|
| 图 1 双层参考向量方法产生参考点示意图 Fig. 1 Schematic diagram of the reference point generated by the two-layer reference vector method |
1.3 归一化处理方法
现实中一些MaOP的目标值范围和量纲不尽相同,为方便求解,需要对个体的目标值进行归一化处理,这样可使获得的计算结果更为可靠。以最小化MOP为例,其归一化过程如下;首先确定解群在各目标函数fi(i=1, …, m)上的最小值fimin和最大值fimax,据此构造最小值向量Fmin= (f1min, …, fmmin)T和最大值向量Fmax=(f1max, …, fmmax)T; 然后将种群个体x的目标值利用式(3)进行归一化:
| $ \bar{f}_i(x)=\frac{f_i(x)-F_i^{\min }}{F_i^{\max }-F_i^{\min }}。$ | (3) |
多目标和高维多目标进化算法种群个体在目标空间中的位置不断变化,意味着个体的收敛性和多样性是动态变化的。算法的总体目标是希望种群不断逼近MaOP真实的Pareto前沿且能保持多样性。因此,算法需要解决以下3个问题:①可以自适应地度量解个体在进化过程中的收敛性和多样性,以动态刻画个体在目标空间中的变化;②希望构造一个标量化指标度量解个体的性能,以便直接比较解个体的优劣;③新的指标函数不引入额外参数以方便使用。基于上述考虑提出适应度指标ICD,同时评估解个体的收敛性与多样性,随着进化过程推进动态地调整解个体收敛性与多样性所占比例,从而使得算法能获取高质量的解集。
设(w1,w2,…,wN)为高维目标空间中一组均匀分布的参考向量,个体i为种群P(规模为N)中任一个体,fit为第t代种群中个体i的目标值向量,‖fit‖为解个体i的目标值向量的模,即在目标空间中个体i与目标空间中理想点之间的距离(规范目标空间中的理想点即为空间坐标系的原点),θt, i, j表示第t代种群中个体i与其最邻近参考向量wj的夹角,则适应度指标ICD(i,wj)可定义如下:
| $ I_{\mathrm{CD}}\left(i, w_j\right)=a \cdot\left\|f_i^t\right\|+b \cdot \frac{\theta_{t, i, j}}{\gamma_{w_j}}, $ | (4) |
其中,a=(tmax-t)/tmax,b=t/tmax,t为进化代数计数器,tmax为算法最大的进化代数,且a+b=1。γwj表示参考向量wj与其他参考向量wi之间的最小夹角,其值由公式(5)确定:
| $ {\gamma _{{w_j}}} = \mathop {\min }\limits_{i \in [1, \cdots , N], i \ne j} < {w_i}, {w_j} > 。$ | (5) |
通常,一组参考向量一旦产生,γwj即为一定值。由于公式(4)中的θt, i, j为锐角弧度,其值一般较小,为在进化后期强调多样性,利用γwj放大多样性比重。ICD由表征收敛性和多样性的两项式相加,而且公式(4)右边第1项值越小表明个体越靠近PF,右边第2项值越小表明个体越靠近均匀分布的参考向量。总体上,ICD值越小表明个体质量越高。
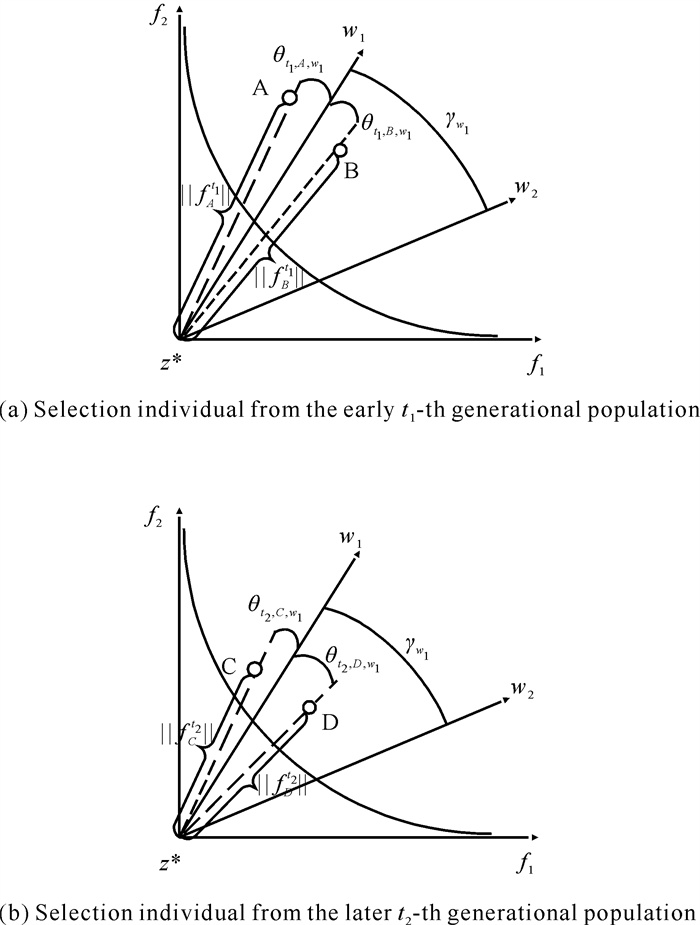
进一步利用示意图解释ICD的机制,如图 2所示。图 2(a)中设种群早期进化代数为t1,则公式(4)右边的系数a和b满足a>b,而且个体A和个体B关联到同一参考向量w1,A到原点的欧氏距离为‖fAt1‖,其与w1之间的夹角为θt1, A, w1;B到原点的欧氏距离为‖fBt1‖,其与w1之间的夹角为θt1, B, w1。此外,离参考向量w1最近的参考向量为w2,它们之间的夹角为γw1。在进化前期,ICD将更注重收敛性,由图 2(a)可知‖fBt1‖ < ‖fAt1‖。根据公式(4)中系数a和b的定义,早期阶段系数a较大,而θt1, A, w1与θt1, B, w1在较小系数b的作用下,它们之间的差距较小,不影响择优的结果,个体B将保留至下一代。
|
| 图 2 基于ICD的个体择优机制 Fig. 2 ICD-based individual selection mechanism |
如图 2(b)所示,设种群进化后期代数为t2,这时ICD中的系数a < b,个体C、D与参考向量w1相关联,C与原点之间的欧氏距离为‖fCt2‖,其与w1之间的夹角为θt2, C, w1;D与原点之间的欧氏距离为‖fDt2‖,其与w1之间的夹角为θt2, D, w1。设w1与其最近的参考向量w2之间的夹角为γw1。ICD在进化后期更注重多样性,由图 2(b)可知θt2, C, w1 < θt2, D, w1,且此时系数b较大,‖fCt2‖和‖fDt2‖在较小系数的作用下,二者相差甚微,不影响择优的结果,个体C将保留至下一代。
一般地,算法的初始种群随机产生,种群的收敛性和分布性通常较差,这一时期需要促使种群朝PF方向进化。经过若干次迭代后,种群个体逐渐靠近PF,但此时种群多样性通常不够理想,种群中有些个体容易聚集,有些个体则分布稀疏,总体上种群的多样性较差。因此需要在进化后期强调个体的多样性,以改善高维多目标进化算法的总体性能。ICD在进化过程中动态调整解个体收敛性与多样性比例,从而改善解集质量。
3 MOEA/ICD算法 3.1 利用ICD划分种群MOEA/ICD算法在迭代过程中需要选择较优个体参与下一代繁殖,因此利用ICD对种群个体进行分层排序。其基本思想是选择能较好地优化参考向量集的个体,并将其置于最靠前的位置,使它们位于第1层次;随后将这些解个体移走,采用同样的方式获得第2层次……如此反复,直至种群中所有个体被分配至相应层次为止。
具体地,设种群P的规模为N,(w1,w2,…,wN)为一组均匀分布的参考向量,i为种群P中任一个体,且i定义为记录(结构体)类型。其中i.rank表示个体层次域,i.value表示个体在参考向量w下的适应度指标值域。如果两个个体在同一参考向量下获得相同ICD,则分别计算它们距离理想点(原点)的欧氏距离。算法1给出了ICD排序算法的流程。
算法1 : ICD排序算法
输入:种群P,参考向量集W
输出:排序后的种群PS
1. for all i∈P do //初始化种群个体
2. i.rank ←i.value ←∞;
3. end for
4. for all w∈W do
5. for all i∈P do
6. i.value ←ICD(i,w);
7. end for
8. 基于种群P中各个体的ICD值以及欧氏距离进行升序排列;
9. rank←1;
10. for all i∈P do
11. i.rank ←min{ i.rank,rank};
12. rank ← rank+1;
13. end for
14. end for
15. 输出排序后的种群PS.
3.2 多样性保持策略基于支配关系的MOEA算法通常采用非支配排序方法对种群分层,然后依据个体层级从高到低择优一定数目的个体进入下一代并保持种群规模不变。而当在某个层级上只能选择部分个体时则需要采取某种环境选择策略促进种群多样性,其中代表性做法包括NSGA-Ⅱ的拥挤距离度量方法[11],RPD-NSGA-Ⅱ[16]利用PBI函数的d2距离择优个体等。但已有的一些环境选择策略大都偏向多样性而在一定程度上忽视了收敛性,基于此,采用ICD评估最末层级上的个体,以选择收敛性和多样性均较好的个体进入下一代。
具体地,假设算法需要从第k个层级Fk上择优部分个体,那么多样性保持策略就将F1至Fk-1层级上的个体i (i∈|F1∪F2∪…∪Fk-1|)与参考向量wj(j=1,2,…,N)进行关联。关联方法是找到与个体i具有最小θt, i, j的参考向量wj,并计算关联到wj的个体数目ρj,如此便可获得各参考向量所关联的个体数目,不妨记作: ρ1,…,ρN。假设参考向量wj上关联个体的数目最小,计算wj与Fk层级上相关联的个体数目ρj。若ρj>1,则根据公式(4)计算Fk上相关联个体的ICD值,并选择具有最小ICD值的个体加入下一代;若ρj=1,则将该个体直接加入下一代,且后面不再考虑参考向量wj。如此反复,直至下一代种群填满为止。该多样性保持策略利用个体与参考向量之间的夹角而非常用的欧氏距离,其原因在于欧氏距离在高维目标空间中不能有效地度量个体之间的距离,而角度的度量则能较好地反映出高维目标空间中的分布性。
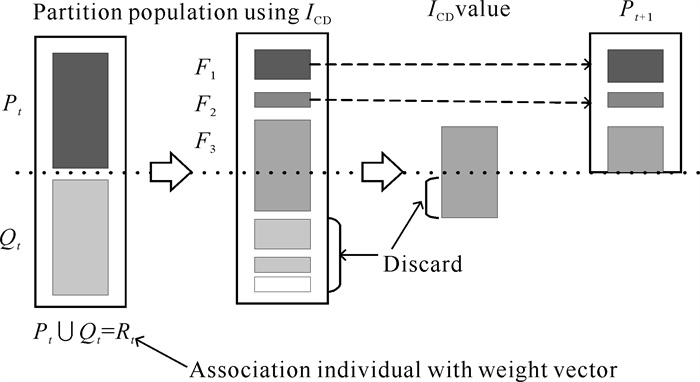
3.3 MOEA/ICD算法流程在前面叙述的基础上,将ICD嵌入经典的NSGA-Ⅱ算法框架中,设计一种基于ICD的高维多目标进化算法MOEA/ICD。新算法利用ICD评估个体的质量,并根据个体的ICD值对种群进行分层和环境选择。图 3以MOEA/ICD算法第t代为例描述算法的运行机制,算法2则给出了MOEA/ICD算法的流程。MOEA/ICD算法的第1步生成规模为N的初始种群P0,利用双层参考向量方法产生一组均匀分布的参考向量;算法从第2步开始进行迭代过程;第3-5步利用仿二进制交叉和多项式变异产生子代种群;第6步合并子代和父代种群;第7-9步实施归一化处理;第10步保留合并种群的边界点;第11步利用ICD排序算法对合并种群进行分层;第12,13步利用3.2节的多样性保持方法在最末层级Fk上择优部分较优个体加入下一代;第14步形成完整的下一代种群;第15步更新代数计数器;第16步while循环结束;第17步输出最末代种群Pmaxgen。
|
| 图 3 MOEA/ICD算法的运行机制 Fig. 3 Running mechanism of MOEA/ICD |
算法2: MOEA/ICD算法
输入:种群规模N,MaOP问题目标数目m,最大迭代次数Tmaxgen
输出:最末代种群Pmaxgen
1. 初始化
1.1 初始化代数计数器t=0;
1.2 在待解问题的可行决策空间内随机产生N个初始个体组成初始化种群P0,并计算各个体的目标值向量{F1(0),…,FN(0)};
1.3 利用双层权值向量生成方法产生一定数目的参考向量: W←two_layered_generation_method(m,H1,H2);
2. while (t < Tmaxgen)
3. 构建交配池: Ptmat=Mating_selection(Pt);
4. 重组运算: Ptrec=Recombination(Ptmat);
5. 变异运算: Ptoffs=Mutation(Ptrec);
6. 合并子种群和父种群:Rt=Pt∪Ptoffs;
7. 计算最小目标值向量Fmin;
8. 计算最大目标值向量Fmax;
9. 归一化处理: Rt← (Rt,Fmin,Fmax);
10. 保留Rt中的边界点;
11. 利用算法1的ICD排序算法划分Rt以获得若干非支配层: [F1,F2,…]←based_nondomination_sorting(Rt,W);
12. 确定最小的k值,使其满足|F1∪ F2∪…∪Fk|≥N,S=|F1∪ F2∪…∪Fk-1|;
13. 利用3.2节中的多样性保持策略在Fk层选择(N-|F1∪F2∪…∪Fk-1|)个解个体加入S;
14. Pt+1 =S;
15. 更新代数计数器t=t+1;
16. end while
17. 输出最末代种群Pmaxgen.
设算法种群规模为N,待解MaOP目标数为m,决策空间维度为n,算法最大迭代次数为Tmaxgen,则算法MOEA/ICD的时间复杂度分析如下:第1步初始化阶段包含3个子步,其中初始化迭代计数器的时间为O(1),产生初始群体P0的时间为O(Nn),计算种群个体目标函数值向量的时间为O(Nm),因此第1步的时间复杂度为O(1)+O(Nn)+O(Nm)=max(O(Nn),O(Nm))。算法从第2步进入迭代阶段,循环体内构建交配池、重组运算、变异运算和合并种群的时间复杂度均为O(Nn)。第7-9步计算最小和最大目标函数值向量以及归一化过程所需时间均为O(Nm)。第10步保留边界点的时间为O(Nm)。第11步利用ICD排序方法对种群进行分层的时间复杂度为O(N2(logN+m))。第12步确定最小的k值使得前面(k-1)层上的个体数目小于N,而前面k层上个体数目大于N,其算法复杂度为O(N)。第13步多样性保持策略的时间为O(N2)。因此,循环体内的时间复杂度为O(N2(logN+m))。由于算法共执行Tmaxgen代,因此整个循环体执行的时间为O(N2Tmaxgen(logN+m))。第17步输出最末代种群的时间为O(Nm)。综上,算法总时间复杂度为max(O(Nn),O(Nm))+O(Nn)+O(Nm)+ O(N2Tmaxgen(logN+m))=O(N2Tmaxgen(logN+m))。
由上可知,MOEA/ICD的时间复杂度取决于利用ICD排序算法对种群进行分层的时间复杂度。当前一些代表性的高维多目标进化算法的时间复杂度多为O(mN2),如NSGA-Ⅲ[12]、DAV-MOEA[17]等,显然基于ICD指标的分层方法的时间复杂度与这些代表性算法的非支配排序方法处于相同水平。但由于ICD动态地度量了解个体收敛性与多样性方面的总体性能,因此较之其他一些排序方法其具有一定的优势。
4 实验与分析 4.1 测试问题实验选取DTLZ[18]系列的DTLZ1-DTLZ4问题,以及MaF[19]系列的MaF1-MaF4问题为测试问题,其原因在于:首先,这些测试问题的目标数可以扩展,本研究将考虑3-、5-、8-、10-和15-目标的测试实例;其次,这些测试问题真实的PF是已知的,便于计算性能指标;最后,这些测试问题的PF具有不同的特征,能够对MOEA算法构成较大挑战。表 1给出了这两个系列的测试问题所具有的特征。
| 测试问题 Test problem |
特征 Features |
| DTLZ1 | Linear,multi-modal |
| DTLZ2 | Concave |
| DTLZ3 | Concave,multi-modal |
| DTLZ4 | Concave,biased |
| MaF1 | Linear |
| MaF2 | Concave |
| MaF3 | Convex,multi-modal |
| MaF4 | Concave,multi-modal |
4.2 性能指标
IGD指标[20]度量了真实Pareto前沿到所获的近似Pareto前沿之间的距离。由于实验中测试问题真实PF是已知的,通过在真实PF上均匀采样若干解点,计算采样点到算法获得的近似Pareto解点之间的距离,这样既能反映解集的收敛性又能反映其多样性。一般而言,IGD指标值越小,表示近似解集的收敛性和多样性越好。
假设P是MOP真实PF的代表解集,A是算法获得的近似Pareto解集,IGD指标可利用公式(6)进行计算:
| $ \operatorname{IGD}(A, P)=\frac{1}{|P|} \sum\limits_{i=1}^{|P|} \operatorname{Dist}_i , $ | (6) |
式(6)中,
为减少随机因素对性能评估的影响,实验中各算法在每一个测试实例中均独立执行30次(每次使用不同的随机数种子)以获得IGD指标的均值和方差。另外,实验利用显著水平为0.05的Wilcoxon秩和检验来分析各算法获得近似解集的性能在统计意义上的差异,符号“+”“-”和“=”分别表示对比算法的IGD值明显优于、劣于和无差别于MOEA/ICD。
4.3 实验结果为验证MOEA/ICD算法的有效性,选取5种代表性的高维多目标进化算法NSGA-Ⅲ[12]、RVEA[13]、θ-DEA[21]、MOEA/D-M2M[22]和RPD-NSGA-Ⅱ[16]为对比算法,考察6种算法在DTLZ和MaF系列测试问题上的IGD性能。为公平起见,各对比算法的参数采用其原始文献的建议值,例如:RVEA的惩罚参数α取值2,调整参考向量频度的参数δ取0.1;MOEA/D-M2M的参数k取值10。实验中所有算法的评估次数设为50 000次;测试问题的决策变量数目均取30;3-目标测试问题的种群规模为91,5-目标测试问题的为210,8-目标测试问题的为156,10-目标测试问题的为275,15-目标测试问题的为135。由于NSGA-Ⅲ算法采用二元锦标赛方法择优个体,所以它的种群规模在3-、5-、8-、10-、15-目标情形下分别取值92, 212, 156, 276和136。
表 2给出了6种算法在3-、5-、8-、10-和15-目标DTLZ1-DTLZ4测试实例上获得的IGD均值和方差。其中,MOEA/ICD在13个测试例上获得了最佳IGD均值(每一行最佳值用粗体突出显示,下同),MOEA/ICD和RVEA分别获得了4个和3个最佳的IGD均值。相比之下,NSGA-Ⅲ、MOEA/D-M2M和RPD-NSGA-Ⅱ无一能获得最佳的IGD均值。从表 2的Wilcoxon秩和检验结果(表中最末一行)来看,MOEA/ICD算法相对于NSGA-Ⅲ、RVEA、θ-DEA、MOEA/D-M2M和RPD-NSGA-Ⅱ算法所获得的净胜得分(优于的数目减去劣于的数目,下同)分别为14, 7, 9, 18和18。总体上,本文算法较之其他对比算法在DTLZ系列问题上具有显著较优的IGD性能。
| 测试问题 Test problem |
目标数目 Objective number |
NSGA-Ⅲ | RVEA | θ-DEA | MOEA/D -M2M | RPD -NSGA-Ⅱ | MOEA/ICD |
| DTLZ1 | 3 | 7.4545e+0 (2.47e+0)- | 1.0341e+1 (3.91e+0)- | 6.6101e+0 (2.56e+0) = | 5.2731e+1 (1.72e+1)- | 1.3899e+1 (5.10e+0)- | 5.5663e+0 (1.80e+0) |
| 5 | 3.7111e+1 (1.06e+1)- | 1.8799e+1 (5.66e+0)- | 1.7645e+1 (4.68e+0)- | 7.1589e+1 (1.30e+1)- | 1.8462e+1 (7.39e+0)- | 8.3161e+0 (2.44e+0) | |
| 8 | 2.4805e+1 (7.78e+0)- | 9.1055e+0 (4.24e+0)- | 8.7720e+0 (3.35e+0)- | 6.4727e+1 (1.52e+1)- | 1.7052e+1 (6.56e+0)- | 4.0488e+0 (7.96e-1) | |
| 10 | 4.5351e+1 (1.35e+1)- | 1.2646e+1 (3.40e+0)- | 1.4366e+1 (4.21e+0)- | 6.6837e+1 (1.42e+1)- | 2.1388e+1 (5.55e+0)- | 4.8230e+0 (1.33e+0) | |
| 15 | 1.2979e+1 (5.31e+0)- | 1.5074e+0 (8.26e-1)- | 2.8831e+0 (1.21e+0)- | 1.0043e+2 (1.15e+1)- | 1.0450e+1 (3.51e+0)- | 1.0534e+0 (4.22e-1) | |
| DTLZ2 | 3 | 5.4478e-2 (4.39e-6)+ | 5.4487e-2 (5.09e-5)+ | 5.4473e-2 (3.11e-6)+ | 1.7708e-1 (6.74e-3)- | 8.4958e-2 (6.07e-3)- | 5.4679e-2 (2.27e-4) |
| 5 | 1.6712e-1 (3.63e-4)- | 1.6621e-1 (2.50e-4)+ | 1.6602e-1 (1.70e-4)+ | 5.4951e-1 (1.97e-2)- | 1.9131e-1 (3.31e-3)- | 1.6656e-1 (2.26e-4) | |
| 8 | 3.7086e-1 (9.61e-2)- | 3.1761e-1 (3.77e-4)= | 3.1924e-1 (8.70e-4)- | 8.5874e-1 (1.92e-2)- | 4.3396e-1 (1.46e-2)- | 3.1802e-1 (7.96e-4) | |
| 10 | 5.1846e-1 (8.17e-2)- | 4.2995e-1 (2.27e-3)- | 4.3607e-1 (2.16e-3)- | 8.6580e-1 (1.99e-2)- | 4.7178e-1 (1.19e-2)- | 4.2765e-1 (2.46e-3) | |
| 15 | 7.5905e-1 (5.27e-2)- | 6.2878e-1 (6.65e-3)- | 6.2840e-1 (1.45e-3)- | 1.2914e+0 (2.28e-1)- | 7.5995e-1 (2.21e-2)- | 6.2524e-1 (9.43e-4) | |
| DTLZ3 | 3 | 2.0628e+1 (7.31e+0)- | 3.6360e+1 (9.89e+0)- | 2.1227e+1 (7.22e+0)- | 1.5005e+2 (4.73e+1)- | 3.4214e+1 (9.83e+0)- | 1.6019e+1 (4.97e+0) |
| 5 | 9.5911e+1 (2.63e+1)- | 7.8262e+1 (2.15e+1)- | 6.1138e+1 (1.43e+1)- | 2.3218e+2 (4.10e+1)- | 5.6769e+1 (1.80e+1)- | 2.8617e+1 (7.48e+0) | |
| 8 | 1.2298e+2 (3.31e+1)- | 3.5939e+1 (1.09e+1)- | 3.6386e+1 (1.12e+1)- | 2.1109e+2 (4.66e+1)- | 6.4598e+1 (1.90e+1)- | 1.1277e+1 (4.33e+0) | |
| 10 | 2.5056e+2 (1.02e+2)- | 5.9076e+1 (1.75e+1)- | 7.4363e+1 (2.10e+1)- | 2.0937e+2 (3.78e+1)- | 6.1859e+1 (1.72e+1)- | 2.0963e+1 (6.13e+0) | |
| 15 | 2.5746e+2 (8.43e+1)- | 1.2915e+1 (6.36e+0)- | 1.4142e+1 (5.92e+0)- | 3.4878e+2 (4.30e+1)- | 5.0703e+1 (1.66e+1)- | 1.6737e+0 (9.17e-1) | |
| DTLZ4 | 3 | 1.6813e-1 (2.10e-1)+ | 7.0716e-2 (8.90e-2)+ | 2.6067e-1 (2.92e-1) = | 1.2314e-1 (8.53e-3)+ | 8.2820e-2 (4.99e-3)+ | 1.9842e-1 (2.51e-1) |
| 5 | 1.6818e-1 (7.75e-4)+ | 1.6618e-1 (2.68e-4)+ | 1.7447e-1 (4.54e-2)+ | 5.8214e-1 (1.97e-2)- | 1.9221e-1 (4.98e-3)- | 1.8252e-1 (6.11e-2) | |
| 8 | 4.0708e-1 (1.01e-1)- | 3.2779e-1 (2.78e-2) = | 3.2315e-1 (1.18e-3) = | 9.4490e-1 (3.67e-2)- | 4.1564e-1 (1.01e-2)- | 3.5119e-1 (5.79e-2) | |
| 10 | 4.7962e-1 (3.31e-2)- | 4.4065e-1 (3.00e-3) = | 4.4973e-1 (2.17e-3)- | 1.0154e+0 (4.22e-2)- | 4.6492e-1 (7.09e-3)- | 4.4004e-1 (2.56e-3) | |
| 15 | 7.1571e-1 (4.09e-2)- | 6.3020e-1 (6.76e-3)+ | 6.2857e-1 (2.91e-4)+ | 2.1270e+0 (3.72e-1)- | 7.1887e-1 (2.14e-2)- | 6.4095e-1 (1.66e-2) | |
| +/-/= | 3/17/0 | 5/12/3 | 4/13/3 | 1/19/0 | 1/19/0 | / | |
| Note:where the best result on each test instance is shown in bold | |||||||
表 3给出了6种算法在3-、5-、8-、10-和15-目标MaF1-MaF4测试实例上获得的IGD均值与方差。其中,MOEA/ICD算法获得了12个最佳的IGD均值,NSGA-Ⅲ、θ-DEA、RVEA、RPD-NSGA-Ⅱ、MOEA/D-M2M获得最佳IGD均值的数目分别为4, 3, 1, 0和0。从表 3的Wilcoxon秩和检验结果(表中最末一行)来看,MOEA/ICD算法相对于NSGA-Ⅲ、RVEA、θ-DEA、MOEA/D-M2M和RPD-NSGA-Ⅱ的净胜得分分别为9, 14, 10, 20, 14。由此可见,MOEA/ICD在求解MaF系列问题时要显著优于其他对比算法。究其原因,MOEA/ICD算法利用ICD动态平衡种群中各个体的收敛性与多样性,有利于算法总体上获得较优的解题效果;其他算法由于未采用动态度量解个体质量的策略,在对种群实施精确调控方面尚有提升空间, 因而它们获得的解群质量显然不如MOEA/ICD。
| 测试问题 Test problem |
目标数目 Objective number |
NSGA-Ⅲ | RVEA | θ-DEA | MOEA/D-M2M | RPD-NSGA-Ⅱ | MOEA/ICD |
| MaF1 | 3 | 6.5979e-2 (1.54e-3)+ | 8.4145e-2 (4.35e-3)- | 7.6460e-2 (2.34e-3)- | 1.8420e-1 (1.02e-2)- | 1.0667e-1 (1.50e-2)- | 7.0286e-2 (5.57e-4) |
| 5 | 1.9552e-1 (1.20e-2)- | 2.9148e-1 (2.16e-2)- | 2.1915e-1 (2.17e-2)- | 3.7667e-1 (1.20e-2)- | 2.0436e-1 (1.95e-2)- | 1.7488e-1 (1.53e-3) | |
| 8 | 3.0018e-1 (1.95e-2) = | 5.0982e-1 (5.44e-2)- | 3.0963e-1 (1.66e-2) = | 4.1329e-1 (1.53e-2)- | 4.5483e-1 (5.80e-2)- | 3.0765e-1 (3.61e-3) | |
| 10 | 2.9271e-1 (1.58e-2)+ | 5.5991e-1 (7.20e-2)- | 3.1698e-1 (1.10e-2)- | 4.2019e-1 (3.08e-2)- | 4.7158e-1 (6.86e-2)- | 3.0960e-1 (2.86e-3) | |
| 15 | 3.5068e-1 (1.36e-2)+ | 6.1635e-1 (6.84e-2)- | 3.5196e-1 (1.39e-2)+ | 4.7726e-1 (4.83e-2)- | 6.2192e-1 (6.05e-2)- | 3.5718e-1 (4.40e-3) | |
| MaF2 | 3 | 4.0696e-2 (1.22e-3)+ | 4.9010e-2 (2.05e-3)+ | 4.0047e-2 (5.03e-4)+ | 1.5399e-1 (9.93e-3)- | 6.1936e-2 (5.95e-3)+ | 7.4935e-2 (4.86e-4) |
| 5 | 1.1653e-1 (2.98e-3)+ | 1.1494e-1 (1.71e-3)+ | 1.2615e-1 (2.74e-3)+ | 2.4922e-1 (9.56e-3)- | 1.2374e-1 (4.90e-3)+ | 1.5438e-1 (1.95e-3) | |
| 8 | 2.5162e-1 (7.15e-2)- | 4.1987e-1 (1.68e-1)- | 2.0078e-1 (1.30e-2)- | 2.3484e-1 (4.12e-3)- | 2.1163e-1 (1.07e-2)- | 1.6089e-1 (1.96e-3) | |
| 10 | 2.2341e-1 (2.39e-2)- | 4.3166e-1 (1.52e-1)- | 2.0559e-1 (7.95e-3)- | 2.1089e-1 (2.30e-3)- | 2.1574e-1 (7.70e-3)- | 1.6704e-1 (1.28e-3) | |
| 15 | 2.6410e-1 (6.65e-2)- | 7.3576e-1 (9.39e-2)- | 3.2595e-1 (4.40e-2)- | 2.5400e-1 (9.24e-3)- | 2.1509e-1 (5.39e-3)- | 2.0087e-1 (2.00e-3) | |
| MaF3 | 3 | 3.8598e+2 (3.02e+2)- | 9.5666e+3 (3.80e+4)- | 3.7297e+2 (3.12e+2)- | 5.6365e+4 (2.56e+4)- | 3.7295e+4 (9.48e+4)- | 1.2295e+2 (7.34e+1) |
| 5 | 2.2778e+4 (4.27e+4)- | 7.3262e+3 (3.42e+3)- | 4.1012e+3 (3.02e+3)- | 9.6377e+4 (3.43e+4)- | 9.0486e+5 (1.97e+6)- | 1.3591e+3 (8.03e+2) | |
| 8 | 3.7591e+7 (8.92e+7)- | 3.1551e+3 (1.76e+3)- | 1.6325e+3 (8.29e+2)- | 7.7039e+4 (2.82e+4)- | 4.3048e+6 (1.43e+7)- | 1.9881e+2 (2.26e+2) | |
| 10 | 1.4822e+9 (4.27e+9)- | 6.8989e+3 (2.72e+3)- | 8.2338e+3 (6.69e+3)- | 5.6802e+4 (1.99e+4)- | 1.1579e+6 (1.18e+6)- | 1.1429e+3 (8.63e+2) | |
| 15 | 2.7447e+7 (5.39e+7)- | 2.6404e+2 (2.08e+2)- | 3.8706e+3 (7.57e+3)- | 1.3420e+5 (3.21e+4)- | 1.2338e+6 (2.55e+6)- | 4.4572e+0 (8.37e+0) | |
| MaF4 | 3 | 7.7987e+1 (3.34e+1)- | 6.1600e+1 (2.28e+1)- | 5.7416e+1 (2.31e+1)- | 8.0470e+2 (2.08e+2)- | 1.1281e+2 (5.36e+1)- | 2.9838e+1 (1.07e+1) |
| 5 | 9.5565e+2 (2.38e+2)- | 6.2472e+2 (2.00e+2)- | 4.1842e+2 (1.21e+2)- | 3.8006e+3 (9.11e+2)- | 5.0424e+2 (1.90e+2)- | 3.5451e+2 (9.63e+1) | |
| 8 | 4.8076e+3 (1.91e+3)- | 2.1262e+3 (1.05e+3)- | 1.7980e+3 (7.51e+2)- | 2.6115e+4 (8.19e+3)- | 2.6135e+3 (1.55e+3)- | 8.1744e+2 (3.77e+2) | |
| 10 | 2.8219e+4 (8.23e+3)- | 9.5076e+3 (5.21e+3) = | 8.4051e+3 (2.55e+3) = | 1.0224e+5 (2.86e+4)- | 9.2182e+3 (3.96e+3) = | 9.2364e+3 (3.97e+3) | |
| 15 | 1.4214e+5 (9.05e+4)- | 2.5685e+4 (1.94e+4) = | 1.2330e+4 (1.05e+4)+ | 2.2401e+6 (1.23e+6)- | 4.1230e+4 (3.63e+4) = | 1.9898e+4 (3.42e+3) | |
| +/-/= | 5/14/1 | 2/16/2 | 4/14/2 | 0/20/0 | 2/16/2 | / | |
| Note:where the best result on each test instance is shown in bold | |||||||
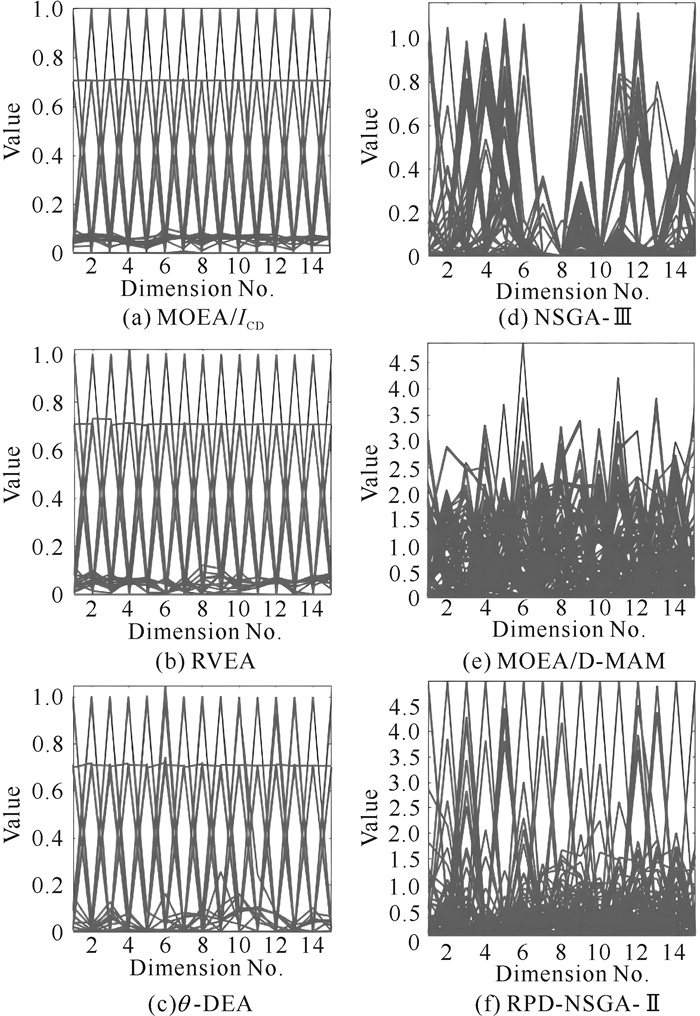
为直观地显示算法求解结果,图 4展示了6种算法在15-目标的DTLZ2 [简记为DTLZ2(15)]测试实例上获得近似解集的平行坐标。此处的近似解集为各算法在30次独立运行中所获得的、最接近于IGD均值的解集合。从图 4可知,MOEA/ICD、RVEA和θ-DEA等3个算法在该测试实例上获得解群的收敛性和分布性均较好,而MOEA/D-M2M和RPD-NSGA-Ⅱ算法所获解集的收敛性差,NSGA-Ⅲ则在第6-8个目标上的分布性差。因此,MOEA/ICD算法在DTLZ2(15)测试实例上获得了较好的收敛性与多样性。DTLZ2测试问题具有凹型的Pareto前沿,其对算法的全局搜索能力构成了挑战。
|
| 图 4 6种算法在15-目标的DTLZ2测试实例上获得的近似集 Fig. 4 Approximate solution sets obtained by six algorithms on DTLZ2(15) test instance |
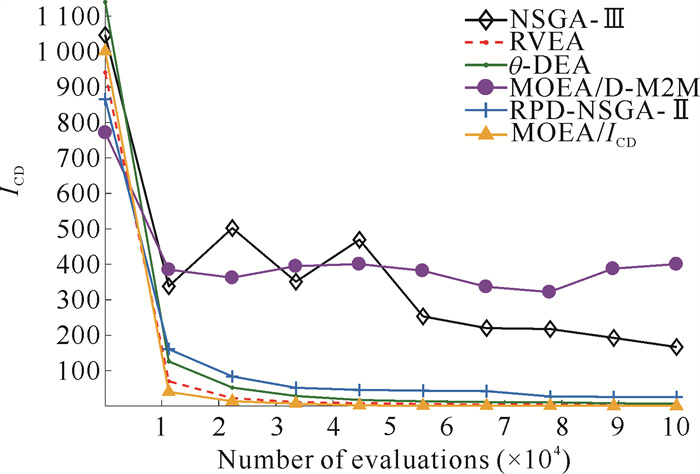
此外,为直观呈现6种算法的收敛速度,图 5描绘了各算法在15-目标的DTLZ3测试实例上获得的IGD值随评估次数(EN)增长而变化的轨迹。为获得稳定且可靠的结果,各算法在测试实例上均独立执行30次,每次运行所需的最大评估次数为1×105。从图 5可以看出,随着评估次数的增加,6种算法所获得的IGD均值总体上表现出变小的趋势。但相对而言,MOEA/ICD算法获得的IGD均值是最好的,其次是RVEA算法,之后是θ-DEA和RPD-NSGA-Ⅱ,而MOEA/D-M2M与NSGA-Ⅲ相对较差。MOEA/ICD与RVEA算法在经历初始约1×104次评估后,它们的IGD均值能较快地下降至一个相对较小的值,而在后续进化过程中,它们的IGD均值呈现出缓慢变小的趋势。以上结果表明相比其他5种算法,MOEA/ICD算法在15-目标的DTLZ3测试实例上能较快地获得高质量的近似解集。
|
| 图 5 6种MOEA算法在15-目标的DTLZ3测试问题上获得的IGD均值变化曲线 Fig. 5 Curves of IGD obtained by six algorithms on DTLZ3(15) test instance |
5 结论
鉴于目前MOEA算法中一些基于参考向量(参考点)方法或基于标量化效用函数方法存在的不足,本研究将基于参考向量的方法和进化算法的迭代过程相结合,提出一种能同时考虑收敛性和多样性的适应度指标ICD,并将ICD嵌入NSGA-Ⅱ算法框架中,设计了一种高维多目标进化算法MOEA/ICD。在DTLZ和MaF系列测试问题上将新算法与其他5种高效的高维多目标进化算法进行实验对比,结果表明本研究算法具有较优的收敛性和多样性优势。由此得出,MOEA/ICD是一种颇具前景的高维多目标进化算法。未来将利用更复杂的高维多目标优化问题和一些实际应用的高维多目标优化问题测试MOEA/ICD,以不断改善其性能。
| [1] |
FALCÓN-CARDONA J G, COELLO COELLO C A. Indicator-based multi-objective evolutionary algorithms: a comprehensive survey[J]. ACM Computing Surveys, 2020, 53(2): 1-35. |
| [2] |
谢承旺, 余伟伟, 闭应洲, 等. 一种基于分解和协同的高维多目标进化算法[J]. 软件学报, 2020, 31(2): 356-373. |
| [3] |
ZHANG Z X, CAO Y, CUI Z H, et al. A Many-objective optimization based intelligent intrusion detection algorithm for enhancing security of vehicular networks in 6G[J]. IEEE Transactions on Vehicular Technology, 2021, 70(6): 5234-5243. DOI:10.1109/TVT.2021.3057074 |
| [4] |
ZHU Z. A hybrid indicator many-objective optimization algorithm for selection and delivery of disaster relief materials problem[J]. Concurrency and Computation: Practice and Experience, 2021, 33(6): e5948. |
| [5] |
PAN L Q, LI L H, HE C, et al. A subregion division-based evolutionary algorithm with effective mating selection for many-objective optimization[J]. IEEE Transactions on Cybernetics, 2020, 50(8): 3477-3490. DOI:10.1109/TCYB.2019.2906679 |
| [6] |
YANG S, LI M, LIU X, et al. A grid-based evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(5): 721-736. DOI:10.1109/TEVC.2012.2227145 |
| [7] |
ZOU X, CHEN Y, LIU M, et al. A new evolutionary algorithm for solving many-objective optimization problems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2008, 38(5): 1402-1412. DOI:10.1109/TSMCB.2008.926329 |
| [8] |
ZHU C, XU L, GOODMAN E D. Generalization of Pareto-optimality for many-objective evolutionary optimization[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(2): 299-315. DOI:10.1109/TEVC.2015.2457245 |
| [9] |
LIU Y, ZHU N, LI K, et al. An angle dominance criterion for evolutionary many-objective optimization[J]. Information Sciences, 2020, 509: 376-399. DOI:10.1016/j.ins.2018.12.078 |
| [10] |
TIAN Y, CHENG R, ZHANG X, et al. A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2019, 23(2): 331-345. DOI:10.1109/TEVC.2018.2866854 |
| [11] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [12] |
DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part Ⅰ: solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601. DOI:10.1109/TEVC.2013.2281535 |
| [13] |
CHENG R, JIN Y, OLHOFER M, et al. A reference vector guided evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(5): 773-791. DOI:10.1109/TEVC.2016.2519378 |
| [14] |
LI K, DEB K, ZHANG Q, et al. An evolutionary many-objective optimization algorithm based on dominance and decomposition[J]. IEEE Transactions on Evolutionary Computation, 2015, 19(5): 694-716. DOI:10.1109/TEVC.2014.2373386 |
| [15] |
DAS I, DENNIS J E. Normal-boundary intersection: a new method for generation the Pareto surface in nonlinear multi-criteria optimization problems[J]. Journal of Optimization, 1998, 8(3): 631-657. |
| [16] |
ELARBI M, BECHIKH S, GUPTA A, et al. A new decomposition-based NSGA-Ⅱ for many-objective optimization[J]. IEEE Transactions on Systems, Man and Cybernetics: Systems, 2018, 48(7): 1191-1210. DOI:10.1109/TSMC.2017.2654301 |
| [17] |
谢承旺, 余伟伟, 郭华, 等. DAV-MOEA: 一种采用动态角度向量支配关系的高维多目标进化算法[J]. 计算机学报, 2022, 45(2): 317-333. |
| [18] |
DEB K, THIELE L, LAUMANNS M, et al. Scalable test problems for evolutionary multi-objective optimization[C]//ABRAHAM A, JAIN L, GOLDBERG R. Evolutionary Multiobjective Optimization. Advanced Information and Knowledge Processing. London: Springer, 2005: 105-145.
|
| [19] |
CHENG R, LI M, TIAN Y, et al. A benchmark test suite for evolutionary many-objective optimization[J]. Complex & Intelligent Systems, 2017, 3(1): 67-81. |
| [20] |
ISHIBUCHI H, MASUDA H, TANIGAKI Y, et al. Modified distance calculation in the generational distance and inverted generational distance[C] // EMO 2015: Evolutionary Multi-criterion Optimization. Cham, Switzerland: Springer, 2015: 110-125.
|
| [21] |
YUAN Y, XU H, WANG B, et al. A new dominance relation-based evolutionary algorithm for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(1): 16-37. DOI:10.1109/TEVC.2015.2420112 |
| [22] |
LIU H B, GU F Q, ZHANG Q F. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(3): 450-455. DOI:10.1109/TEVC.2013.2281533 |



