网络舆情具有直接、突发、多元等特点,一旦管理不当,可能就会对社会产生不利影响。某些舆论事件受新消息或新活动的影响,显现出群体观点倾向的完全逆转,这种舆情的非典型性特征称为舆情逆转。因此,提出一个高质量的舆情逆转分析模型有助于全面、准确地研判舆情,对构建和谐的网络环境具有积极意义。
观点演化模型作为一种有效的工具被用来调查各个领域的民意动态。其中,Deffuant-Weisbuch(DW)[1]观点演化模型是一种连续观点交互模型,该模型假设两个个体只有在观点值差值小于置信阈值时才会进行交互。DW模型的优势在于能够表现出两个意见相近个体的观点演化过程,因此本文利用DW这一特性,对现实中个体接收到不同观点产生不同态度的这一过程进行建模。DW模型也存在一些缺陷,两个观点相近的个体,即使有交互观点的意愿,但由于在社交网络结构中的状态已经发生改变,有可能不再关心本话题,那么就无法产生观点交互过程,从而最终影响整个观点演化过程。传统的DW模型没有考虑这一因素,只是把所有意见相近个体挑选出来进行观点交互,不能较好地反映社交网络中观点演化动态。
本文拟改进传统的DW观点演化模型,扩展观点交互个体的范围,利用经典的传染病传播模型,表现个体在信息传播过程中状态的变化,通过提取初始信息源发布者观点变化的特征,提出一个网络舆情逆转模型。该模型具有以下特点:①信息传播与观点演化过程相结合,符合网民真实的微博转发、微博评论行为;②设定信息质量、传播率、可信度、观点倾向和逆转信息发布时间,为深入分析逆转信息对舆情逆转的影响提供数据与建议支持。
1 相关工作舆情逆转这一社会现象受到业界学者的广泛关注。黄远等[2]基于社会物理学指出“舆情逆转”现象的实质是舆情演变过程中各方博弈的结果,运用结构平衡理论归纳出舆情逆转的4种类型。高红阳等[3]引入后真相时代特征,分析舆情逆转的成因,并对调控途径进行探讨。如果仅从社会学、新闻学等视角探讨舆情逆转,并不能深入地刻画舆情逆转模式,也不能反映社交网络中个体观点演化过程以及个体传播状态的变化。
研究者以复杂网络和统计物理学为工具对舆论演变过程进行探索,将社交网络中的个体看作有决策力和自主性的智能体,对这些智能体进行交互建模,使观点形成和演化可以通过仿真来计算和呈现。其中,基于观点动力学的建模研究在舆论演化领域得到广泛运用,主要将观点分为两大类型:离散观点,用整数0,+1,-1分别表示中立、支持和反对;连续观点,用在区间[0, 1]的实数表达,边界0和1分别表示完全反对和完全赞同。典型的离散观点模型包括Sznajd模型[4]及其扩展,连续观点模型包括DW和Hegselmann-Krause(HK)[5]有界信任模型。上述模型的自然演化结果往往是群体观点达成共识、碎片化或极化。然而,社会公众事件的发展规律通常受到外在因素制约,不能自然演化。为刻画这一过程,本文借鉴连续观点和离散行为模型[6]的思想,将个体在社交平台上所表达的态度:支持、中立和反对态度视为离散行为。这样,个体的观点值则被视为态度背后的成因。Huang等[7]提出考虑网络意见领袖和组织氛围两大因素的舆情逆转模型,并指出恶意信息的传播是影响逆转现象的重要因素,但未对恶意信息的影响机理进行讨论。Zhu等[8]建立一个基于DW的异构模型来分析企业并购的组织规范融合问题,探讨并购后文化规范逆转风险的影响因素,但没有考虑到信息对逆转的作用。Cheng等[9]利用意见气候的概念建立了环境影响函数。吴越等[10]基于微博网络舆情逆转数据的统计分析,结合信息传播和观点演化过程设置多种参数,描述信息对网络舆情逆转过程的影响作用,但没有反映出当个人的观点发生变化时,网络舆情不仅受信息驱使,还会受到周围节点的影响。
基于传染病模型SIR (Susceptible,Infected,Recovered)[11]和SEIR (Susceptible,Exposed,Infected,Recovered)[12]的信息传播模型的提出,为预测真实信息传播过程提供了依据[13]。这类模型的最大缺点是个体间状态转换的概率是固定的,转换因素单一,为了弥补这一缺陷,还须考虑多种因素对个体间状态转换的影响。Li等[14]将观点演化模型和信息传播模型融合,分析影响信息传播的几种因素,提出一种新的HK-SEIR模型,能反映真实信息传播情形,但未对舆情逆转这一特殊情形进行建模。本文在分析舆情逆转真实案例的基础上,从中抽取具有重要作用的参数,构建舆情逆转模型,通过仿真实验对不同参数作用下的舆情逆转过程进行分析,得出有意义的结论。
2 舆情逆转案例分析近年来,由于部分媒体报道的片面失实、网民习惯先入为主地发表评论等种种原因,许多事件当事的某一方在官方介入调查之前就已经被网络舆论声讨。网络舆情逆转事件时有发生,2018年重庆万州一辆大巴车与一辆小轿车相撞后冲破护栏掉入江中,在有关部门未公布事件结果之前,小轿车女司机成为舆论声讨对象,官方调查后,公交车坠江原因是乘客与司机争执互殴导致车辆失控。2020年广州一位家长称女儿被班主任体罚至吐血,舆论群情激愤,人们纷纷谴责教师,对母亲和孩子的遭遇表示同情,经过官方调查后,广州白云区公安局发布通报,学生家长为扩大影响而编造谎言。2022年有人发布微博称赵丽颖逃税达4 526万,舆论开始一边倒地抨击艺人失德,但是经官方调查后,上海税务局出面辟谣,该消息属恶意诽谤。
以上述事例中2020年的逆转事件为例,学生家长初始消息发布后网络舆论反应强烈,纷纷声讨老师和学校,这起疑似教师体罚学生的事件迅速成为热点话题。广州白云区教育局于2020年5月31日发布通报,该学生家长为扩大事件影响,故意编造孩子被体罚的谎言,网络舆情发生逆转。据新浪舆情通政企舆情大数据服务平台统计,截至2020年6月1日,该事件在全网共有223.39万条相关信息,网民在传播该消息的同时也发表自身对此事的态度。2020年5月30日13时,距离事件首发6 h,全网信息量规模达到顶峰,多数评论都以批评教师和同情孩子为主。随着时间的推移,话题热度下降。虽然官方澄清,事件逆转,此时有不少人为教师发声,但信息量也不及之前水平。舆情逆转现象扰乱了公共舆论环境,浪费了网络资源,造成公众视听混淆甚至割裂,为舆论危机埋下隐患。
3 网络舆情逆转模型 3.1 Deffuant-Weisbuch模型连续观点DW模型主要研究两个不同观点在置信区间内的交互作用。
设无向图G={V, E′} 表示一个社会网络, 其中V={v1, v2, …, vn}和E′ ⊆{(vi, vj)|vi, vj∈V}分别表示节点(用户)集和边(用户关系)集,节点vi∈V通常被赋予一个[0, 1]的连续观点值,记为oi,而边代表用户的好友关系。
设在t时刻,两个用户vi和vj相遇,若此时两者观点之间的距离小于等于一定的阈值,即|oi(t)-oj(t)|≤ε,两者进行观点更新;若距离超过该阈值,即|oi(t)-oj(t)|>ε,双方保持观点。观点演化规则如下。
当|oi(t)-oj(t)|≤ε成立时,用公式(1)进行观点更新:
| $ \left\{\begin{array}{l} o_i(t+1)=o_i(t)+\mu\left(o_i(t)-o_j(t)\right) \\ o_j(t+1)=o_j(t)+\mu\left(o_j(t)-o_i(t)\right) \end{array}\right. \text { 。} $ | (1) |
当|oi(t)-oj(t)|>ε成立时,保持观点,见公式(2):
| $ \left\{\begin{array}{l} o_i(t+1)=o_i(t) \\ o_j(t+1)=o_j(t) \end{array}\right. \text { 。} $ | (2) |
该模型采用参数μ表示观点差值的接受度,通常取值为[0, 0.5]。
3.2 基于多因素的网络舆情逆转模型根据前一章舆情逆转的实际案例特征,可以作出以下分析:①网络舆论是否发生反转的根本原因在于是否存在与之前报道事实相反的新闻报道,本文在后续讨论中将此类信息称为逆转信息。例如,在“广州教师体罚学生”事件中,公安局关于学生家长造谣的通报信息就是逆转信息。②用户会受其他节点的影响而改变观点。在舆情逆转过程中,发布逆转信息的媒体信息质量对舆情逆转的幅度有较大影响。质量越高,在短时间内转发信息和转变初始看法的用户就会越多。③消息的质量和传播率。逆转新闻发布距离初次发布的时间间隔,这些属性差异显著影响舆情逆转的结果。
本文基于观点①和②构建了一个网络舆情逆转模型。为了区别网络中的不同节点,分别对节点的传播状态属性、观点属性、态度属性和信任属性作出以下设置。
3.2.1 传播状态属性结合SEIR传染病模型,将网络中的用户视为易感节点S,潜伏节点E,传染节点I,免疫节点R。处于S态中的用户表示没有接收到消息但是有能力接收;处于E态的用户已经接收到消息,但是并没有转发和表达观点;处于I态的用户为消息传播用户并表达其观点;处于R态的用户,不参与消息的转发讨论。
3.2.2 观点属性当不同用户接触新闻话题时,会产生一个处于[-1, 1]区间的观点值,且有观点阈值ε,用户只与观点差异处于阈值范围内的节点进行观点交互。
3.2.3 态度属性不同的用户在接受新闻话题时,会根据自己的观点值产生不同的态度。为了更清晰地表达节点的态度变化,将节点vi对初始消息的态度Ai分为支持、中立和反对3种类型,分别用a+、a0、a-表示。
3.2.4 信任属性由于网民的性格、受教育程度和信息接受能力不同,因此会对信源信息产生理解差异。本文将用户vi的信任值记为bi,即用户收到信息的信任阈值。考虑到大多数个体接受信息的能力相近,只有少部分人的接受能力较高或较低,本文设置信任值集合B={b1, b2, …, bn},其中bi(i=1, 2, …, n)满足(0, 1)上的正态分布。在现实生活中,个人信任值bi不是一个恒定常数,而会随着多种因素改变。但由于这一过程具有随机性,且样本数目较大时可均化,因此本文建模时不考虑信任值的波动。信任值bi越接近0,代表用户越开放,因而越容易相信外界观点;相反地,bi越接近1,用户越不易接受外界信息。
3.3 消息传播与观点演化规则本文采用异步方法实现节点的观点倾向和状态更新。每个时步t将更新所有节点的传播状态和观点倾向。类比SEIR传染病模型,每个E态节点有α的概率被感染成为I态节点,有β的概率被感染成为R态节点,每个I态节点有γ的概率被感染成为R态节点。为了构建舆情逆转模型,故作出以下假设。
假设1:信息源节点在t=0时刻处于传染态I,具备一个固定的观点值。该节点通常是事件的当事人或者陈述者,故该节点只负责传播初始信息,其观点值不受周围人的影响而改变。为量化信息质量,本文参考魏静等[15]提出的模型,引入信息质量Q作为衡量信息源发布信息质量的参数,当Q趋近于1时,代表信息质量高,可信度高;当Q趋近于0时,信息质量低,可信度低。
假设2:设信息源节点vs,用来表示最先报道某新闻事件的用户或媒体。当初始信息发布时,vs的观点值os设置为1;而信息源发布逆转信息时,观点值设置为-1。
假设3:信息源之外的普通节点在传播信息时,将信息的内容转述给其他节点,同时附上自己的态度,对应用户在微博平台中转发并评价原文内容的行为。
在初始时刻信息源发布信息时,其周围节点从易感态S转变为潜伏态E,传播状态更新规则如公式(3)所示:
| $ \begin{aligned} & I(s)+E(i) \stackrel{p}{\longrightarrow} \\ & \left\{\begin{array}{l} v_i^{\text {state }}=I, p=\alpha\left(Q \geqslant b_i\right) \\ v_i^{\text {state }}=R, p=\beta\left(Q<b_i\right) \end{array}\right. \end{aligned} $ | (3) |
其中,vistate表示节点vi的传播状态,I(s)表示感染态的信息源节点,E(i)表示易感态的非信息源节点。
本文模型在传统DW模型的基础上作出改进,使每一个时步内个体不只与其他单一个体进行观点交互,而且会与周围多个处于观点阈值内的个体交互。若在t时刻,节点vi的观点值oi(t)和邻居节点vj的观点值oj(t)满足公式|oi(t)-oj(t)|≤ε,则更新观点。同时,还考虑到传播的信息质量Q会对节点的观点演化过程产生影响,综合以上因素,本文对模型作出以下改进。
① 如果信息源发布的消息质量Q大于或等于节点vi的信任阈值bi,则说明该信息能被vi所接受,因此在更新自身观点时,将部分考虑到信息源节点的观点。这一过程可以被形式化表述为公式(4)。
| $ \begin{array}{l} \ \ \ \ \ \ {o_i}(t + 1) = {o_i}(t) + {\mu _2}\left( {{o_s}(t) - {o_i}(t)} \right) + \\ {\mu _1}\sum\nolimits_{j = 1}^{j = 1} {\left( {{o_j}(t) - {o_i}(t)} \right)} , \end{array} $ | (4) |
其中,μ1和μ2分别表示观点的采纳程度,参数越大,采纳程度越高,Nei表示与节点vi相邻的邻居节点集合。
② 如果信息源发布的消息质量Q小于节点vi的信任阈值bi,那么节点就会忽略信息源的观点,因此按照公式(5)更新观点值。
| $ o_i(t+1)=o_i(t)+\mu_1 \sum\nolimits_{\mathrm{Nei}}^{j=1}\left(o_j(t)-o_i(t)\right) 。$ | (5) |
I态节点转发初始消息内容,并表达对该消息的态度。观点值取[-1, 1]内的实数值,本文将连续的观点值映射为三分类的离散态度,规则如公式(6)所示:
| $ \left\{\begin{array}{l} A_i=a_{+}, o_i \geqslant 0.32 \\ A_i=a_0, -0.34<o_i<0.32 。\\ A_i=a_{-}, o_i<-0.34 \end{array}\right. $ | (6) |
该模型的信息传播与观点演化的具体过程如算法1所示。
算法1 消息传播与观点演化规则
输入: os, V={v1, v2, …, vn}, B={b1, b2, …, bn}。
输出: S(t), E(t), I(t), R(t), a+(t), a0(t), a-(t)。
① for t=0 to T do
② for i=0 to n do
③ if vistate= =S并且有I态的邻居节点
④ then vistate←E
⑤ else if vistate= =E then
⑥ if Q≥bi then
⑦ p(vistate←I)=α
⑧ 通过公式(4)计算oi
⑨ 通过公式(6)计算Ai
⑩ else
⑪ p(vistate←I)=α
⑫ if vistate= =I then
⑬ 通过公式(5)计算oi
⑭ 通过公式(6)计算Ai
⑮ else
⑯ p(vistate←I)=β
⑰ end if
⑱ end if
⑲ else if vistate= =I then
⑳ p(vistate←I)=γ
㉑ end if
㉒ end for
㉓ 计算t时刻下节点的数量S(t), E(t), I(t), R(t)和a+(t), a0(t), a-(t)
㉔ end for
㉕ return S(t), E(t), I(t), R(t), a+(t), a0(t), a-(t)。
其中,vistate表示vi节点的状态,S(t)、E(t)、I(t)、R(t)分别表示在t时刻不同状态下节点的数量。a+(t)、a0(t)、a-(t)分别表示t时刻下对初始信息源发布的信息持有支持、中立、反对3种态度的节点数量。
4 结果与分析本文对舆情逆转模型进行仿真实验,设t0为首次传播逆转消息的时刻,分别对同一消息源仅传播初始消息以及同一消息源先传播初始消息,再于t=t0时刻传播逆转消息这两种情形进行仿真,依次调节信息质量、传播率以及逆转消息发布时间,分析其对舆论演化结果的影响。
4.1 社交网络模型为模拟微博平台中用户的节点度分布情况,本文构建了一个与社交网络特性相似的无标度网络Barabasi-Albert (BA)。BA网络有10 000个节点,点与点之间的连边为29 991条,网络密度为0.000 5,平均聚类系数为0.005,节点最大中心度为352,最小中心度为0。网络的节点度分布如图 1所示。本实验模拟真实社交网络中用户的交互,观察观点在多种因素作用下的传播状态以及观点状态随时间变化的过程。
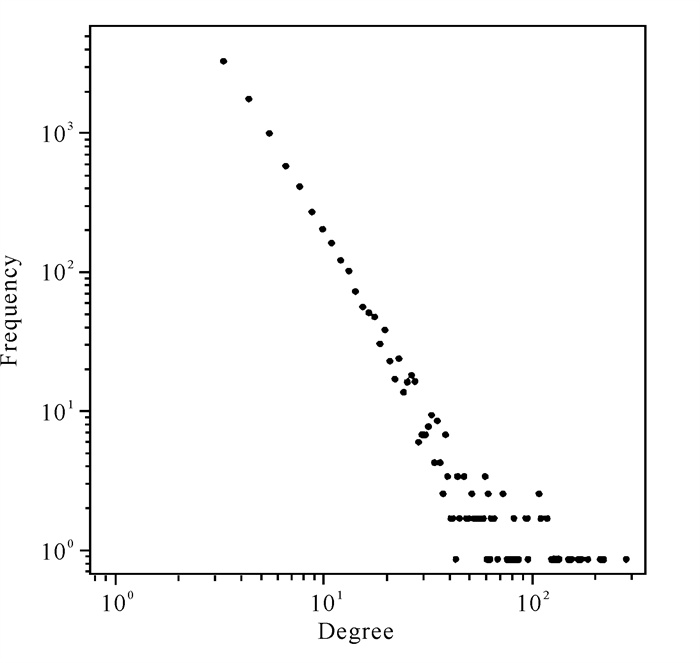
|
| 图 1 BA网络节点度分布 Fig. 1 BA network node degree distribution |
4.2 参数设置
表 1展示了舆情逆转模型中各参数设置的缺省值。信息源节点代表在社交网络中舆情事件的第一个传播者、讲述者,甚至是事件的当事人,故在整个舆情的传播中扮演着重要的角色。在传统的DW模型中,参数μ表示观点差值的接纳程度,一般地,μ在区间[0, 0.5]上取值。为了反映现实世界中信息源节点的重要性,设置了一个比普通节点更大的采纳度μ2,使普通节点在观点演化过程中更多地考虑信息源节点的观点。为不失一般性,实验在生成的BA网络中,对每个网络的普通节点在[-1, 1]上随机赋予初始的观点值,以及在[0, 1]上随机赋予对信息源观点的信任值。
| 符号 Symbol |
取值 Value |
定义 Definition |
| n | 10 000 | Number of network nodes |
| μ1 | 0.2 | Acceptance of opinions on surrounding nodes |
| μ2 | 0.5 | Acceptance of opinions on information source nodes |
| Os | 1 | Initial opinion value of the information source node |
| α | 0.5 | Probability of a node in state E to state I |
| β | 0.4 | Probability of a node in state E to state R |
| γ | 0.2 | Probability of a node in state I to state R |
| oi | [-1, 1] | Opinion value of non-source information node |
| bi | [0, 1] | Trust value of the node |
| Q | (0, 1) | Information quality of the information source |
| ε | 0.3 | Bounded trust parameters |
4.3 初始消息传播
当网络中只有一个初始消息源传播时,调整信息源信息质量Q,其余参数设置如表 1,观察易感态S、潜伏态E、感染态I、免疫态R 4个状态节点数量的变化。随着时间的推移,易感态节点逐渐变为潜伏态(图 2),潜伏态节点根据接收到的信息质量决定是否传播消息。在t=8附近,传染态节点数量达到峰值,并且峰值随着信息源信息质量Q的提升而增大(图 2),说明信息质量Q会影响话题的传播。
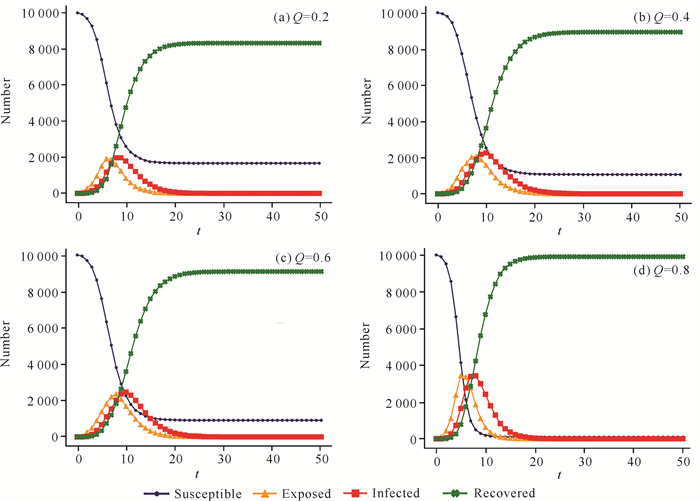
|
| 图 2 仅有初始信息源传播时节点传播状态随信息质量Q的变化 Fig. 2 Changes of point propagation state with information quality Q when only initial information source is transmitted |
以“广州教师体罚学生”事件为例,设蓝色、红色和黄色趋势线分别表示对初始消息的观点持支持态度(支持学生家长)、反对态度(支持老师)以及持中立态度的用户数量。随着时间的推移,3种观点的节点数量均呈先增后减的趋势(图 3),与话题热度的变化趋势相符。
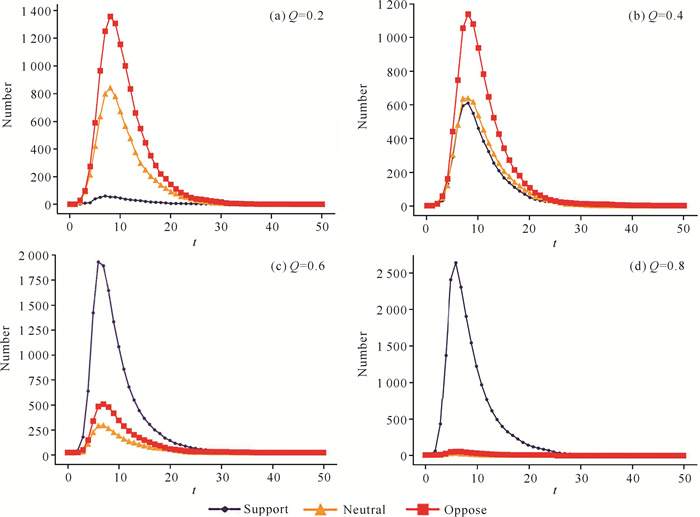
|
| 图 3 仅有初始信息源传播时3种态度的节点数量随信息质量Q的变化 Fig. 3 Number of nodes with three attitudes varies with the information quality Q when only the initial information source is transmitted |
当信息源信息质量Q=0.2时,反对节点居多,说明低质量信息发布反而会招致许多非议;当Q=0.4时,持支持态度的节点数量显著增加,但由于信息质量仍然偏低,持反对态度的节点数量依旧大于支持态度;当Q=0.6时,支持态度的节点数量远超反对节点,用户普遍相信信息源节点发布的消息;当Q=0.8时,持支持态度的节点数量已处于主导地位。以上实验结果表明,模型参数设置与其对应的物理意义较吻合。
4.4 同一信息源的逆转消息传播为验证逆转信息的质量对舆情逆转程度的影响,将初始信息源的信息质量设置为0.5,在t=5时传播逆转信息。为观察逆转信息对节点的影响,在逆转信息发布时,初始信息不再继续传播。调节参数Q、t0和α,固定其他参数,观察持有不同态度节点数量的变化。
逆转信息的质量对舆情逆转有显著影响(图 4)。当逆转信息质量为0.2时,信息质量低于初始信息质量,逆转信息的发布对舆情逆转效果不明显[图 4(a)];当逆转信息质量为0.4时,持反对态度的节点数量较t=5时刻前有所增加,但对初始信息的支持态度仍占舆论主导地位[图 4(b)];当逆转信息质量大于初始信息质量时(t=5),持反对态度的节点数量开始迅速增加,逐渐超过支持态度的节点数量,最终持反对态度的舆论占据主导地位[图 4: (c)(d)]。
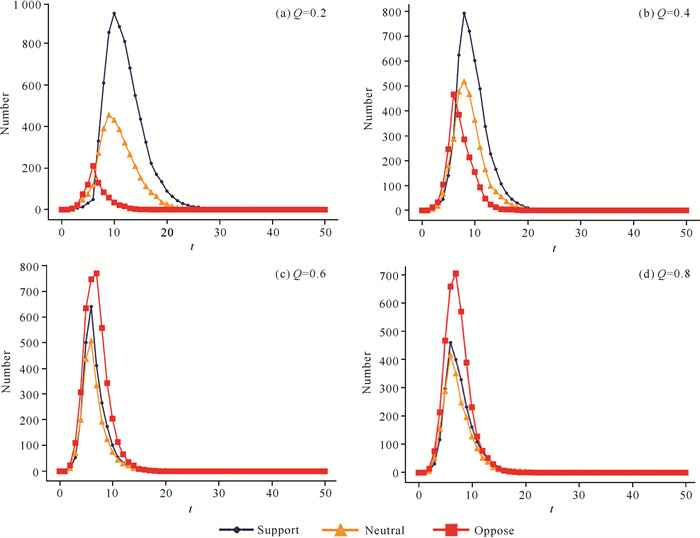
|
| 图 4 初始信息源于t=5发布逆转消息时3种态度的节点数量随Q的变化 Fig. 4 Initial information source from the change in the number of nodes with the three attitudes as Q when the reversal message is released at time t=5 |
为进一步定量地评估舆情逆转情况,用公式(7)来量化舆情逆转的程度,并且探究不同影响因素对舆情逆转的影响。舆情逆转的程度C(t)定义如下:
| $ C(t)=\frac{a_{+}(t)-a_{-}(t)+1}{a_{+}(t)+a_{-}(t)+1}, $ | (7) |
其中,a+(t)表示在t时刻对话题持支持态度的个体数量,a-(t)表示在t时刻对话题持反对态度的个体数量。公式中分子分母经过平滑处理,避免出现分母为零的情况,C(t)的值越小,舆情逆转的程度就越大。
为检验信息质量对舆情逆转的影响,设初始信息质量Q=0.5,其他参数保持不变。图 5显示,当同一信息源发布逆转消息后,两种态度之间的节点数量差异迅速减小,但当逆转信息质量小于初始信息质量时(图中红、蓝折线),在整个舆情演化阶段,C(t)值始终大于0,说明舆情并未发生逆转,支持初始信息的舆论始终占据主导地位;当逆转信息质量大于初始信息质量时,舆情在t=5时刻附近开始发生逆转,逆转幅度与逆转信息质量呈正相关。以上结果说明逆转信息质量对舆情逆转幅度有明显影响。
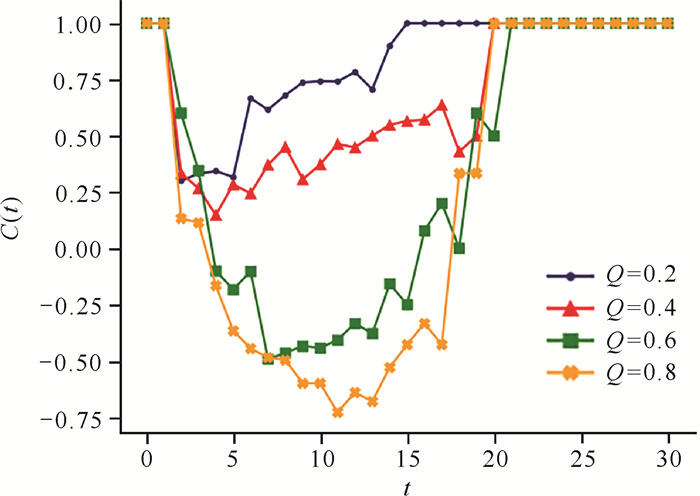
|
| 图 5 同一信息源传播不同质量的逆转信息时舆情的逆转情形 Fig. 5 Reversal situation of public opinion when the same information source transmits reversal news of different quality |
传播率α会影响信息传播速度,α值越大,节点对应的用户越有可能成为传播者。为检验传播率对舆情逆转程度的影响,对初始信息和逆转信息赋予相同的信息质量Q=0.5,并且4次实验都在t=3时刻发布逆转消息。
实验结果如图 6所示,在t=3时刻之前,由于信息质量属于中等水平,支持该信息的节点数量迅速接近持有反对态度的节点数,C(t)会随时间步迅速接近0。由于网络中持两种观点的节点数量增多,两者之间的差异逐渐缩小,因此随着传播率的提升,C(t)下降的速度会更快。该实验证明了这一事实:传播率越高,逆转消息扩散越迅速,舆情逆转程度越大。
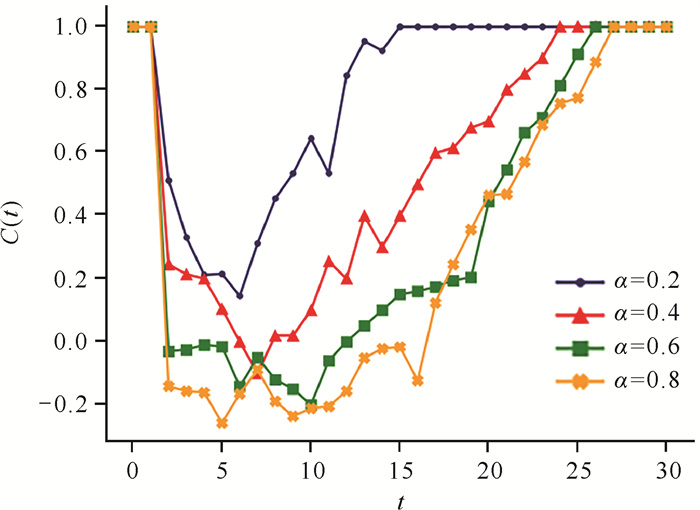
|
| 图 6 同一信息源在不同传播率下传播逆转信息时的舆情逆转情形 Fig. 6 Reversal situation of public opinion when the same information source transmits reversal news under different transmission rates |
为观察在不同时刻下发布逆转信息对舆情逆转的影响,设置4个不同时刻发布逆转信息,其余参数均和前述实验相同,其中逆转信息与初始信息质量均为0.5。同一信息源在t=t0时刻发布逆转信息后,C(t)值随着t0的增长呈不同的变化趋势,C(t)值变为0的速率减慢,并且最低值随逆转信息发布时间后移(图 7)。这意味着舆情逆转的程度随逆转信息发布的滞后而减小,说明信息源越早传播逆转信息,舆情逆转幅度越大。

|
| 图 7 同一信息源于不同时刻发布逆转信息时的舆情逆转情形 Fig. 7 The same information comes from the public opinion reversal situation in which the reversal information is released at different times |
5 结论
本文通过对微博网络舆情逆转数据进行分析,提出了网络舆情逆转模型。仿真实验结果表明:①信息源信息质量与传染态节点数量呈正相关关系,信息源发布的信息质量越高,社交网络中传播信息的节点数量越多;②发布的逆转信息质量如果小于初始信息质量,那么不会发生逆转,而是会依照原先的发展态势继续演变;③如果其他因素相同,逆转信息的质量越高,舆情逆转的幅度就越大;④当初始信息与逆转信息质量一致时,舆情逆转的幅度会随着逆转信息传播率的增大而增大;⑤逆转信息发布的时间越早,舆情逆转速率越快,幅度越大,说明逆转信息传播的时间越早,对舆情逆转越有利。
由于多因素的网络舆情逆转模型与现实环境吻合,因此有助于对网络舆情逆转过程和规律的理解和分析。仿真实验对未来舆情治理具有一定的启发作用,如果希望突发事件能尽快发生逆转,就必须考虑尽快发布高质量的逆转信息,这样才能阻止初始信息继续扩大对社会的影响,对负面舆情起到遏止作用。
| [1] |
WEISBUCH G, DEFFUANT G, AMBLARD F, et al. Meet, discuss, and segregate![J]. Complexity, 2002, 7(3): 55-63. DOI:10.1002/cplx.10031 |
| [2] |
黄远, 刘怡君. 网络舆论反转效应研究[J]. 管理评论, 2016, 28(8): 71-78. |
| [3] |
高红阳, 闫心池, 王珊. 反转新闻成因与治理路径探析——以广州教师涉嫌体罚学生舆情为例[J]. 今传媒, 2021, 29(9): 71-74. DOI:10.3969/j.issn.1672-8122.2021.09.019 |
| [4] |
SZNAJD-WERON K, SZNAJD J. Opinion evolution in closed community[J]. International Journal of Modern Physics C, 2000, 11(6): 1157-1165. DOI:10.1142/S0129183100000936 |
| [5] |
HEGSELMANN R, KRAUSE U. Opinion dynamics and bounded confidence models, analysis and simulation[J]. Journal of Artificial Societies & Social Simulation, 2002, 5(3): 1-33. |
| [6] |
MARTINS A C R. Continuous opinions and discrete actions in opinion dynamics problems[J]. International Journal of Modern Physics C, 2008, 19(4): 617-624. DOI:10.1142/S0129183108012339 |
| [7] |
HUANG C, HU B, JIANG G, et al. Modeling of agent-based complex network under cyber-violence[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 458: 399-411. DOI:10.1016/j.physa.2016.03.066 |
| [8] |
ZHU H, HU B, WU J, et al. Adaptation of cultural norms after merger and acquisition based on heterogeneous agent based relative-agreement model[J]. Simulation: Transactions of the Society for Modeling and Simulation International, 2013, 89(12): 1523-1537. DOI:10.1177/0037549713508301 |
| [9] |
CHENG C, LUO Y, YU C B. Dynamic mechanism of social bots interfering with public opinion in network[J]. Physica A: Statistical Mechanics and its Applications, 2020, 551: 124163. DOI:10.1016/j.physa.2020.124163 |
| [10] |
吴越, 杜亚军, 陈晓亮, 等. 基于新曝光冲突性消息的网络舆论逆转研究[J]. 物理学报, 2016, 65(3): 46-55. |
| [11] |
MA W B, SONG M, TAKEUCHI Y. Global stability of an SIR epidemic model with time delay[J]. Applied Mathematics Letters, 2004, 17(10): 1141-1145. DOI:10.1016/j.aml.2003.11.005 |
| [12] |
MORENO Y, GÓMEZ J B, PACHECO A F. Epidemic incidence in correlated complex networks[J]. Physical Review E, 2003, 68(3): 035103. DOI:10.1103/PhysRevE.68.035103 |
| [13] |
XIE T, WEI Y Y, CHEN W F, et al. Parallel evolution and response decision method for public sentiment based on system dynamics[J]. European Journal of Operational Research, 2020, 287(3): 1131-1148. DOI:10.1016/j.ejor.2020.05.025 |
| [14] |
LI Q, DU Y J, LI Z Y, et al. HK-SEIR model of public opinion evolution based on communication factors[J]. Engineering Applications of Artificial Intelligence, 2021, 100(2): 104192. |
| [15] |
魏静, 贾宇广, 朱恒民, 等. 基于舆情当事人信息质量及群众信任阈值的观点演化研究[J]. 情报杂志, 2022, 41(2): 126-133. |



