2. 西安电子科技大学计算机科学与技术学院, 陕西西安 710071
2. College of Computer Science & Technology, Xidian University, Xi'an, Shaanxi, 710071, China
命名实体识别(Named Entity Recognition,NER)[1]是自然语言处理(Natural Language Processing,NLP)中的一项最基础的任务,其性能的好坏直接影响着下游任务,如关系抽取[2]、机器翻译[3]、知识图谱构建[4]等。目前,命名实体识别主流方法是基于神经网络的监督性学习模型,而命名实体识别数据集中常存在实体类别样本数量较少和实体嵌套现象,导致模型学习实体类别特征的能力较弱。命名实体识别数据集实体类别较少,导致模型识别实体类别时出现正负样本不平衡现象;嵌套实体是指实体内部嵌套了多个命名实体,由于识别嵌套实体属于自然语言处理中较为困难的任务,所以嵌套实体被列为难以识别的实体,嵌套实体过多则导致难易样本不平衡问题,从而影响模型的整体性能。
传统的命名实体识别方法包括基于序列标记[5]的方法、基于超图[6]的方法和基于跨度的方法。其中,基于序列标记的方法通过预测每个字对应的标签来解决嵌套实体;基于超图的方法与序列标记上的解码不同,它是基于实体嵌套结构来构建超图,从而解码超图上的实体;基于跨度的方法通过枚举[7]或识别边界[8]来提取跨度,然后对跨度进行分类。尽管上述方法在解决实体嵌套问题上具有一定的可行性,但是在实体类别较少的情况下仍显不足。最近,利用外部知识增强实体类别特征学习的方法日益受到人们的关注。Li等[9]和Xue等[10]将命名实体识别转换为机器阅读理解(MRC)任务,通过定义实体类别的先验知识来构造实体类型的查询。除此之外,自训练[11-15]的方法也广泛用于图像处理和自然语言处理中,并以此来解决少样本问题。Lin等[16]在图像处理领域为损失函数增添平滑因子来缓解正负难易样本不平衡的问题。Li等[17]为损失函数引入密度函数,使模型较少关注某些离散群点。基于前述分析,本研究提出一种基于改进损失函数的实体类别平衡优化算法,拟通过为交叉熵损失函数添加平滑系数和权重因子,在缓解正负样本不平衡的同时缓解难易样本的不平衡问题。
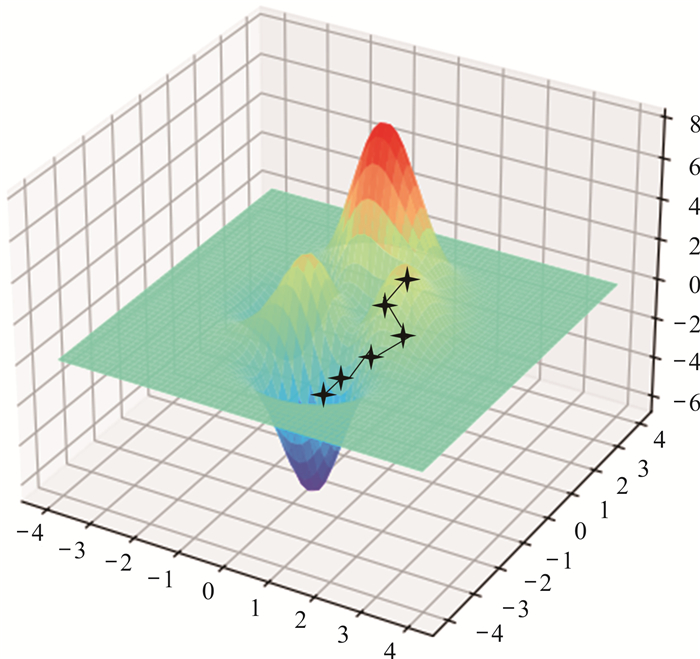
1 损失函数在深度学习中,损失函数用于计算模型预测值与真实值之间的差距,以判断模型算法的优劣性。损失函数常用于回归问题与分类问题,而命名实体识别属于分类问题中的二分类问题,其对应的损失函数为0-1损失。0-1损失属于不连续的分段函数,所以只有当函数为连续凸函数,并在任意取值下是0-1损失函数上界时,才能正确地构造出其代理函数[18]。梯度是一种迭代法,在求解模型损失函数最小值时,就是通过梯度下降来一步步迭代求解(图 1,图中星星代表梯度下降走过的路径),而且通过梯度下降,可以使损失函数最小,从而反向调节模型参数。
|
| 图 1 损失函数梯度下降图 Fig. 1 Loss function gradient descent diagram |
1.1 梯度下降
梯度下降的计算过程就是沿着梯度的方向向下逐步求解极小值,也是求解局部最优的过程。其迭代公式为
| $a_{k+1}=a_k+\rho_k \bar{s}^{(k)},$ | (1) |
式中,ak表示上一步梯度下降的结果;s(k)表示梯度的负方向;ρk表示搜索方向的步长,步长的长短直接影响模型在梯度下降过程中的收敛速度,步长过大可能导致模型无法获得局部最优,步长过小则导致收敛速度过慢。
1.2 交叉熵损失函数命名实体识别由于涉及的是分类问题,所以常用交叉熵损失函数作为模型中用于梯度下降的损失函数。在分类的应用中,交叉熵损失函数的最小化交叉熵等价于最小化观测值和估计值的相对熵,因此它提供了一个无偏估计的代理损失,是在分类任务中应用最广的损失函数,公式如下:
| $g(p, y)=\left\{\begin{array}{cc}-\log _2(p), & y=1 \\ -\log _2(1-p), & \text { 其他 }\end{array} ,\right.$ | (2) |
式中,y∈{-1,1},p∈[0, 1],y是一个真实类,p是模型对标签为y=1的类的估计概率。
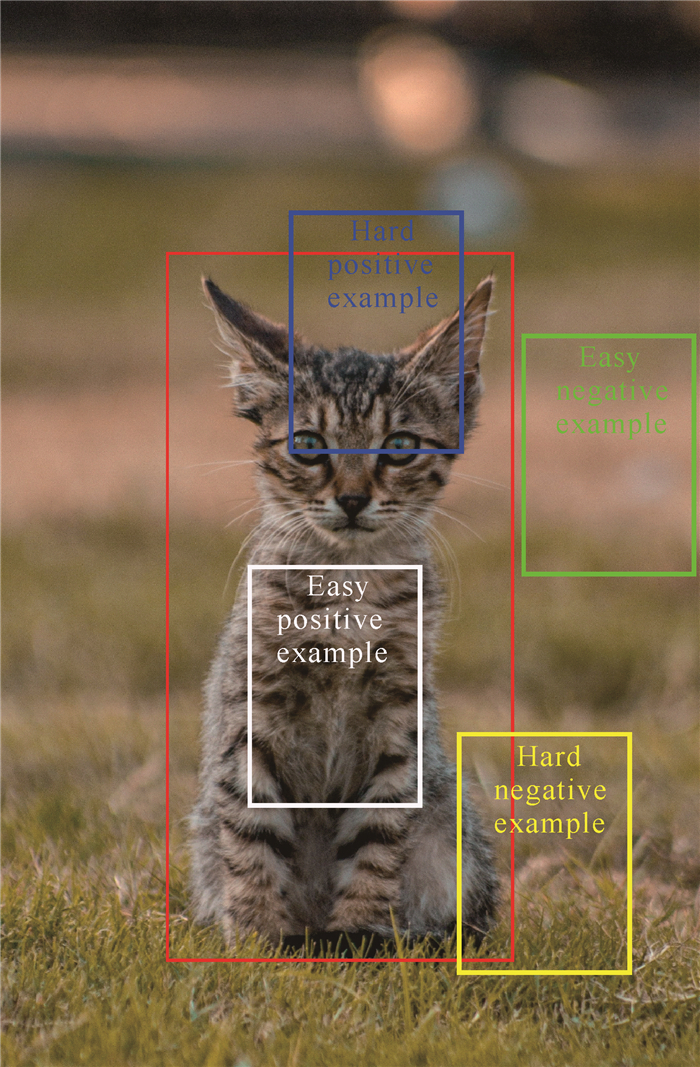
2 改进的交叉熵损失函数在分析命名实体识别数据中发现,数据集常存在实体类别较少和嵌套的问题,导致模型不能很好地识别。交叉熵损失函数并没有关注数据间的不平衡,而是单纯地度量两个概率分布间的差异,因此无法缓解上述不平衡问题。本研究借鉴目标检测领域中难易样本平衡的方法来解决该类问题,目标检测中难易样本例子如图 2所示。
|
| 图 2 目标检测领域中难易样本识别例子 Fig. 2 Examples of hard and easy sample recognition in the field of target detection |
从图 2可以观察到,目标检测领域同样存在难易样本不均衡,即难(易)样本太多,易(难)样本太少的问题,使得普通的交叉熵损失函数在对模型反向调节的过程中过度关注于不重要的信息,而忽略了重要的信息。基于上述思想,本研究在交叉熵损失函数的基础上引入一个平滑系数pt[16]:
| $p_t=\left\{\begin{array}{cc}(1-p)^\theta, & y=1 \\ p^\theta, & \text { 其他 }\end{array}\right.,$ | (3) |
式中,θ≥0是一个关注度系数,可以通过设置不同的θ来减少或增强对难易样本的关注度,从而缓解难易样本不平衡所导致的模型识别较差问题。
由于命名实体识别数据集中存在较为普遍的正负样本不平衡现象,本研究在交叉熵损失函数的基础上同时引入一个权重系数α[19],以调节正负样本的损失权重和,得到最终改进的损失函数:
| $F_{\text {loss }}=\alpha p_t g(p, y) 。$ | (4) |
另外,可通过数学分析来直观地了解改进的损失函数的作用。例如,为了平衡难易样本,当θ=2和p=0.9时,针对易分类样本,其关注度降低了100倍;而当p=0.1时,样本明显是一个难分类样本,模型识别存在困难,通过增添平滑系数,在降低易分类样本损失权重贡献的基础上又重点关注了难分类样本。同时,通过添加权重系数α来降低(提高) 某一方样本过多(少)对损失权重的贡献。
3 实验仿真及分析 3.1 数据集本研究提出基于改进损失函数的实体类别平衡优化算法,实验数据均来自公共数据集MSRA和ACE05,数据样本的详细信息如表 1所示。
| 数据集 Dataset |
标签 Label |
训练集 Train dataset |
测试集 Test dataset |
| MSRA | LOC (Place name) | 86 849 | 7 291 |
| ORG (Organization) | 103 261 | 6 977 | |
| PER (Person) | 51 738 | 5 824 | |
| ACE05 | PER (Person) | 21 771 | 2 470 |
| ORG (Organization) | 10 643 | 1 261 | |
| GPE (Geography/society/politics) | 13 327 | 2 092 | |
| LOC (Place name) | 2 350 | 263 | |
| FAC (Facility) | 2 568 | 246 | |
| VEH (Vehicle) | 1 027 | 155 | |
| WEA (Weapon) | 628 | 42 |
3.2 评价指标
本研究利用改进的损失函数对命名实体识别任务进行验证,实验结果用精准率(P)、召回率(R)和F1值来说明。其中,精准率表示为模型预测为正的样本占所有正样本的比重,召回率表示为样本中的正样本被预测正确的比重,F1值表示为精准率和召回率的调和平均,公式如下:
| $P=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}},$ | (5) |
| $R=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}},$ | (6) |
| $F 1=\frac{2 \times P \times R}{P+R}$ | (7) |
式中,TP表示把实体正类预测为正类的数量,FP表示把实体负类预测为正类的数量,FN表示把实体正类预测为负类的数量。
3.3 实验环境及参数设置本研究是在tensorflow 1.14和python 3.6的环境下进行实验。设置模型在训练、测试时的batch_size为128;为降低在模型训练过程中出现的过拟合现象,将dropout设置为0.5;学习率设置为0.001,Adam作为模型的优化器;改进损失函数中的θ分别设置为0,1,2,4,α设置为0.25以验证其有效性。BERT预训练模型选择base版本。
3.4 实验结果为验证改进损失函数的实体类别平衡优化算法的有效性,本研究利用BERT和BERT+Floss进行实验对比,如表 2所示。从表 2可以看出,改进损失函数算法的实体类别平衡优化有效地提高了实体识别的性能。具体表现为在MSRA数据集中F1值提高了0.91%;在ACE05数据集中,数量最少的实体类别VEH和WEA,F1值分别提高1.36%和5.05%,总体F1值提高了1.53%。原因在于:MSRA数据集嵌套实体较少,实体类别样本较多,正负难易样本不平衡的情况较少,所以在识别性能上提升较小;ACE05数据集中存在大量的嵌套实体和个别实体类别样本较少的情况,通过改进损失函数反向调节模型,缓解了模型在正负难易样本识别上的不平衡。
| 数据集 Dataset |
模型 Model |
标签 Label |
精准率(%) P(%) |
召回率(%) R(%) |
F1 (%) |
| MSRA | BERT | LOC | 91.88 | 94.36 | 93.10 |
| ORG | 84.70 | 95.03 | 89.57 | ||
| PER | 97.49 | 97.44 | 97.47 | ||
| Total | 91.21 | 95.45 | 93.28 | ||
| BERT+Floss | LOC | 93.93 | 94.24 | 94.08 | |
| ORG | 89.17 | 93.60 | 91.33 | ||
| PER | 97.64 | 96.88 | 97.26 | ||
| Total | 93.56 | 94.82 | 94.19 | ||
| ACE05 | BERT | PER | 84.69 | 90.28 | 87.40 |
| ORG | 74.55 | 83.33 | 78.70 | ||
| GPE | 80.78 | 83.17 | 81.96 | ||
| LOC | 61.82 | 64.15 | 62.96 | ||
| FAC | 69.23 | 61.36 | 65.06 | ||
| VEH | 69.34 | 71.43 | 70.37 | ||
| WEA | 60.53 | 69.70 | 64.79 | ||
| Total | 79.35 | 83.96 | 81.59 | ||
| BERT+Floss | PER | 87.72 | 89.61 | 88.66 | |
| ORG | 77.40 | 85.17 | 81.10 | ||
| GPE | 82.96 | 82.63 | 82.80 | ||
| LOC | 63.94 | 62.74 | 63.33 | ||
| FAC | 69.78 | 71.36 | 70.56 | ||
| VEH | 81.73 | 63.91 | 71.73 | ||
| WEA | 73.33 | 66.67 | 69.84 | ||
| Total | 82.18 | 84.09 | 83.12 | ||
| Note: the bolded data in the table is the optimal value | |||||
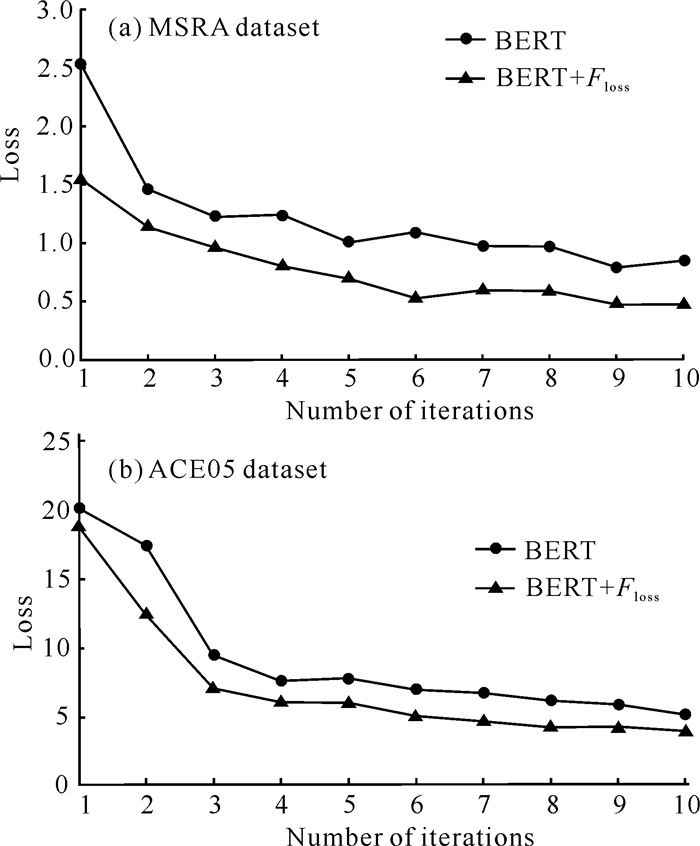
结合改进的损失函数,在两个数据集上对模型进行实验观察(图 3)。从图 3可以观察出,结合了改进损失函数的命名实体识别模型相比于结合交叉熵损失函数的命名实体识别模型,损失函数收敛速度明显加快,其原因在于为交叉熵损失函数添加平滑系数和权重系数后,模型更加关注于难识别样本, 同时平衡正负样本,可以有效提高模型识别性能。
|
| 图 3 损失函数迭代变化 Fig. 3 Iterative change of loss function |
平滑系数中不同的θ值,会对模型产生不同的影响,结果如表 3所示。从表 3可以看出,当θ=0时,改进后的损失函数与原损失函数相同;当θ=1时,由于平滑系数变化不大,导致其对难识别样本关注度不高,性能提升较小;当θ=2时,两个数据集均达到了最优性能,原因在于此时的损失函数能够很好地抑制易识别样本,而且也能很好地关注难识别样本;当θ=4时,由于平滑系数调节过大,导致模型过度关注于难识别样本,反而忽略了易识别样本,导致模型识别性能降低。因此,从实验结果可以看出,当数据集难易样本不平衡时,改进损失函数所呈现出的性能提升较为明显;当数据集中难易样本较为平衡时,模型提升性能较小。由此说明,本研究改进的损失函数适合于数据集存在难易样本不平衡的情况,并表明了其有效性。
| 数据集 Dataset |
平滑系数 θ |
精准率(%) P(%) |
召回率(%) R(%) |
F1(%) |
| MSRA | 0 | 91.21 | 95.45 | 93.28 |
| 1 | 92.04 | 95.32 | 93.65 | |
| 2 | 93.56 | 94.82 | 94.19 | |
| 4 | 90.65 | 95.02 | 92.78 | |
| ACE05 | 0 | 79.35 | 83.96 | 81.59 |
| 1 | 80.79 | 83.02 | 81.89 | |
| 2 | 82.18 | 84.09 | 83.12 | |
| 4 | 78.32 | 83.13 | 80.65 | |
| Note: the bolded data in the table is the optimal value | ||||
为验证权重系数和改进损失函数的通用性,在其他交叉熵模型MRC[9]上对数据集ACE05进行验证,实验结果如表 4所示。实验结果表明,为交叉熵损失函数添加权重系数后,F1值有一定提升,并且改进损失函数在其他交叉熵模型上同样取得了不错的性能提升,由此验证了改进损失函数的通用性。上述结果说明公式(4)中权重系数对于平衡样本存在一定贡献,并且改进损失函数在其他交叉熵模型上也同样有效。
| 模型 Model |
权重系数 α |
精准率(%) P(%) |
召回率(%) R(%) |
F1(%) |
| MRC | 0.1 | 79.09 | 80.12 | 79.60 |
| 0.2 | 81.62 | 80.94 | 81.28 | |
| 0.4 | 82.99 | 82.66 | 82.82 | |
| 0.8 | 83.41 | 83.54 | 83.47 | |
| MRC+Floss | 0.1 | 83.78 | 84.01 | 83.89 |
| 0.2 | 84.47 | 84.81 | 84.63 | |
| 0.4 | 83.89 | 83.65 | 83.77 | |
| 0.8 | 83.55 | 83.74 | 83.64 | |
| Note: the bolded data in the table is the optimal value | ||||
4 结论
本文提出了一种基于改进损失函数的实体类别平衡优化算法,缓解了命名实体识别中的正负难易样本不平衡所导致的模型识别性能较低的问题。通过在两个公共数据集上的实验,证明了本文所提出的改进策略在命名实体识别分类模型中的有效性。在未来工作中,将根据不同数据集的特点,探索进一步的改进方式。
| [1] |
许力, 李建华. 基于BERT和BiLSTM-CRF的生物医学命名实体识别[J]. 计算机工程与科学, 2021, 43(10): 1873-1879. |
| [2] |
XIONG C Y, LIU Z, CALLAN J, et al. Towards better text understanding and retrieval through kernel entity salience modeling [C]//The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval. Ann Arbor, MI: SIGIR, 2018: 575-584.
|
| [3] |
SONG J, KIM S, YOON S. AligNART: non-autoregressive neural machine translation by jointly learning to estimate alignment and translate [C]//Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2021: 1-14.
|
| [4] |
JI S, PAN S, CAMBRIA E, et al. A survey on knowledge graphs: representation, acquisition, and applications[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 33(2): 494-514. |
| [5] |
HUANG Z, XU W, YU K. Bidirectional LSTM-CRF models for sequence tagging [Z/OL]. (2015-08-09)[2022-09-12]. https://arxiv.org/pdf/1508.01991.pdf.
|
| [6] |
LU W, ROTH D. Joint mention extractionand classification with mention hypergraphs [C]//Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2015: 857-867.
|
| [7] |
SOHRAB M G, MIWA M. Deep exhaustive model for nested named entity recognition [C]//Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2018: 2843-2849.
|
| [8] |
ZHENG C, CAI Y, XU J, et al. A Boundary-aware neural model for nested named entity recognition [C]//Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP). Stroudsburg, PA: ACL, 2019: 357-366.
|
| [9] |
LI X, FENG J, MENG Y, et al. A unified MRC framework for named entity recognition [C]//Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics. Stroudsburg, PA: ACL, 2020: 5849-5859.
|
| [10] |
XUE M, YU B, ZHANG Z, et al. Coarse-to-Fine pre-training for named entity recognition [C]//Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP). Stroudsburg, PA: ACL, 2020: 6345-6354.
|
| [11] |
NIU Y, JIAO F, ZHOU M, et al. A Self-Training me-thod for machine reading comprehension with soft evidence extraction [C]//Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics. Stroudsburg, PA: ACL, 2020: 3916-3927.
|
| [12] |
MENG Y, ZHANG Y, HUANG J, et al. Distantly-supervised named entity recognition with noise-robust learning and language model augmented self-training [C]//Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2021: 10367-10378.
|
| [13] |
ZOPH B, GHIASI G, LIN T Y, et al. Rethinking pre-training and self-training [C]//LAROCHELLE H, RANZATO M, HADSELL R, et al. Advances in Neural Information Processing Systems 33. [S. l. ]: NeurIPS, 2020: 3833-3845.
|
| [14] |
MI F, ZHOU W, KONG L, et al. Self-training impro-ves pre-training for few-shot learning in task-oriented dialog systems [C]//Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Stroudsburg, PA: ACL, 2021: 1887-1898.
|
| [15] |
DU J, GRAVE É, GUNEL B, et al. Self-training improves pre-training for natural language understanding [C]//Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies. Stroudsburg, PA: ACL, 2021: 5408-5418.
|
| [16] |
LIN T Y, GOYAL P, GIRSHICK R, et al. Focal loss for dense object detection [C]//Proceedings of the IEEE International Conference on Computer Vision. Piscataway, NJ: IEEE, 2017: 2980-2988.
|
| [17] |
LI B, LIU Y, WANG X. Gradient harmonized single-stage detector [C]//Proceedings of the AAAI Conference on Artificial Intelligence. Menlo Park, CA: AAAI, 2019: 8577-8584.
|
| [18] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 121-139, 298-300.
|
| [19] |
XIE S, TU Z. Holistically-nested edge detection [C]//Proceedings of the IEEE International Conference on Computer Vision (ICCV). Piscataway, NJ: IEEE, 2015: 1395-1403.
|


