2. 电子科技大学信息与软件学院, 四川成都 610054
2. School of Information and Software, University of Electronic Science and Technology of China, Chengdu, Sichuan, 610054, China
随着网络技术的蓬勃发展,交互式社交媒体已深入公众日常生活。依托大数据技术和媒体融合技术的全媒体现象,不仅模糊了媒体的边界,还降低了媒体内容制作的门槛[1]。近年来,我国正处于社会结构转型的关键期,极具群体性、破坏性、不确定性的社会安全事件已成为影响国家安全和社会稳定的重要问题之一[2]。当大型群体性事件演变为打、砸、抢、烧的暴恐行为时,事件所引发的风险会对社会稳定和公众安全造成严重威胁[3],如2015年四川邻水事件、2018年江苏镇江退役军人集体维权事件、2019年香港暴乱事件等。由于网络的开放性以及社会安全事件自身的敏感性,导致事件发生时公众意见和情绪大量扩散,在海量话题讨论的冲击下,相关事件极易引发网络群体极化进而产生情绪化和负向化,导致网络舆论失控,推动事件态势升级[4]。社会安全事件发生的同时,某些别有用心者利用信息的模糊性,制造谣言意图带动舆论风向,蓄意煽动网民情绪,鼓动实施极端暴力行为[5],加剧了事件矛盾冲突。
群体性事件场景干扰因素多、不可控性强、社会危害程度大,决策者难以对其态势演变进行准确评估。准确预测社会安全事件发生态势升级的概率,可以为相关部门提前布控预防措施,进而最大程度降低对社会和公众的危害,对维护国家安全和社会稳定具有重要意义。社交媒体上的网络舆论犹如群体性事件演化的传感器,在一定程度上反映或推动了事件的内在发展,舆情数据成为研究预测各类社会安全事件态势升级的重要依据。因此,本文以群体性事件(以下均简称“事件”)为例,以多种社交媒体平台为数据来源,研究事件演变过程中态势发生暴恐转向的风险。
1 相关工作目前,针对事件态势演化问题,国内外学者从以下3个方面展开了广泛研究。
第一,在仿真建模分析中,学者们将事件升级的诱导因素设置为仿真模型的参数,其中在模拟个体偏好和情绪因素对群体聚集影响的结果中发现,个体偏好参数决定了人群聚集状态的改变,情绪因素是行为选择的重要条件,而且在高密度聚集下,负面情绪参数升高更容易主导事件暴力化转向[6-8]。另外,从理论建模角度上来看,Gustafson[9]在1991年至2017年期间非洲和拉丁美洲爆发的群体性事件研究中发现,当社会面临高失业率和粮食价格上涨时,发生暴力升级的可能性较大,表明社会因素也是引发群体事件发生暴力转向的一个重要条件。
第二,在事件趋势演化研究中,学者们利用自然语言分析和聚类算法从社交媒体提取事件的时间特征和内容特征,分析话题对事件舆情演变规律的影响[10],通过对热点主题识别或根据微博帖文及其转发数量的传播特征,预测事件舆情的传播演化机制[11-13]。考虑到群体事件意见领袖或特殊群体在社交媒体的引导作用,Jia等[14]根据微博用户的交互行为在无标度网络模型上研究得出,微博用户观点演变趋向容易受影响力大的节点引导。Deb等[15]通过分析2020年美国大选活动期间超过2.4亿条推文发现,操纵社交媒体舆论风向的两个显著维度分别是机器人水军和注入阴谋或谣言。
第三,在事件风险评估研究中,学者们从事件的原因、管理缺陷、人身安全和应急管理体系4个层面的部分或整体构建指标评估体系或状态模型,并结合专家知识或算法模型量化指标,实现对事件进行事后风险的评估[16-18]。另外,在军事、网络安全和恐怖事件等领域感知预测对象的态势变化时,考虑到对象本身如威胁性、容灾性或破坏性等特点,研究者提出了基于因果关系的定性与定量分析方法[19-21]。事件风险评估的定性与定量研究方法中,专家评价法指的是在相关事件数据不充足时,专家依据自身领域知识经验对事件风险点进行赋值评估,该方法强依赖于主观意识。层次分析法在处理复杂指标时容易出现数据不一致的现象。模糊综合评价法虽然缓和了前两者的缺点,但是对指标体系的交叉信息要求较高[22]。神经网络法虽然具有良好的学习能力,适合复杂模型的研究,但是对结果的可解释性较差。而基于贝叶斯理论的贝叶斯网络(Bayesian Network,BN)可以根据条件概率对节点关系进行因果推理,清晰的网络结构关系链具有较强的可解释性,而且能够很好地处理指标因素复杂、数据不确定的概率推理等问题。
虽然上述文献对事件态势演变研究做出了较大贡献,但目前仍存在以下3个方面的问题:①当前研究在分析事件态势升级的影响因素多集中于情感、个体偏好和意见领袖,缺乏对事件的全局性分析,事件致因维度有待丰富;②事件趋势性主要考虑从舆情演化趋势分析,但舆情演化趋势主要是反映事件的传播特征,无法衡量事件变化的本质特征;③现有研究方法在评估群体性事件态势演变为冲突性、暴力性事件的风险时,主要根据事后统计的人身安全状况或财产的损失程度对风险进行量化,然而对事件行为由初始和平状态转向为暴恐性质的程度性风险的研究相对较少。
针对上述问题,为了丰富群体性事件态势升级方面的研究,推理预测事件态势转向可能程度的量值,本文从定性与定量角度分析,建立对事件态势升级产生影响作用的指标体系。利用模糊理论与贝叶斯理论网络对不确定性事件处理的优势,根据其网络的层次结构链,解释各指标因素对事件发生暴恐转向的影响机理。同时为了避免模糊理论中专家经验知识带来的主观依赖弊端,利用词频-逆文档频率(Term Frequency-Inverse Document Frequency,TF-IDF)算法对事件影响因素进行客观赋权,基于博弈论思想均衡多角度赋权算法,获得最优组合权重。以国内某重大群体性事件作为模型研究案例,利用初始萌发至事件爆发前一天的数据预测该事件在当日发生暴恐转向的风险,为相关部门提供风险预警和及时制定针对性应急方案提供支撑依据。
2 暴恐转向风险预测模型 2.1 暴恐转向风险指标体系构建科学全面的指标评估体系是准确描述事件发生暴恐转向风险的重要前提。李倩倩等[3]在分析我国群体事件特征时,从时间、空间分布特征以及从网络大数据中获得事件形式、类型与涉及人群等因素,从理论角度对我国社会风险治理存在的问题提出针对性建议。Jia等[14]和Deb等[15]的研究表明事件演变趋向与引导者操纵有重要关联。Gustafson[9]发现,当高失业率和粮食价格高上涨率的社会矛盾突出时,发生事件态势升级的数量和程度更为明显。林焰等[23]在研究恐怖袭击的量化分析中讨论了事件发生时机和地区的影响。王朝等[24]从事件的袭击手段、事件组织者和事件影响范围等因素,建立突发事件分级量化标准。为全面考虑促使事件态势升级的影响因素,本文综合我国群体性事件的特点与已有研究贡献,依据指标构建原则[25]建立暴恐转向的指标评估体系,并依据德尔菲法[26]对指标进行多轮修改,最后确定暴恐转向风险指标体系,具体如表 1所示。其中一级指标为A事件时间、B事件地点、C事件主题、D事件规模、E组织人群、F活动方式、G国际因素、H自然因素和I社会矛盾,各二级指标为一级指标的具体指向内容。
| 一级指标 First grade index |
二级指标 Second grade index |
指标含义 Meaning of index |
| A: time | A1:key dates A2:duration time |
Due to historical factors, there is a high probability of significant events occurring on key dates |
| B: location | B1:transportation hub | Negative emotions are easily accumulated in high-density crowd locations and people′s emotions are easily influenced by others |
| B2:downtown area | ||
| B3:landmark building | ||
| C: theme | C1:legal factor C2:electoral factor C3:rights protection |
Mass incidents usually arise from dissatisfaction with feelings of loss of rights |
| D: scale | D1:geographical scope D2:number of participants |
Geographic scope involved and number of participants mark the scale of the event |
| E: organization people | E1:group organization E2:representative figure |
The words and actions of key groups or individuals guide the development of the activity |
| F: activity type | F1:behavior | The activity type can reflect the severity of events |
| G: international factors | G1:overseas public opinion | International public opinion will play a driving role in the development of events |
| H: nature factors | H1:weather | Weather conditions may affect participants′ moods |
| I: social conflicts | I1:economic level I2:local governance |
Social consciousness and organizational form are both the cause of events and the conditions for the evolution of events |
2.2 基于三角模糊数的主观赋权原理 2.2.1 三角模糊数原理
模糊数[27](Fuzzy number)是定义在μ内的模糊集合,对任意变量x,存在μ(x)∈[0, 1],μ为变量x的隶属度函数,又称μ为x的模糊数。其中,三角模糊数(Triangular Fuzzy Number, TFN)作为一种特殊的模糊集合,利用领域专家的经验知识,对描述不确定性、模糊性和部分真实性的信息作出模糊语言评价的一种量化方法,已被应用到决策中表示事件发生的概率程度,相较于定性分析方法,最大限度地减少了人为因素的影响[28]。当A=(a, m, b)的隶属函数μA满足公式(1)时,称A为三角模糊数。Nguyen[29]提出模糊集合的扩充形式,即对任意模糊集合μ,存在参数为λ∈[0, 1]的可信度,将A映射为一定可信度水平的区间数,称为λ-截集,说明A的隶属程度,如公式(2)所示。三角模糊数映射关系如表 2所示。
| $\left\{\begin{array}{c}\mu_A(x)=0, x \leqslant a \\ \mu_A(x)=\frac{x-a}{m-a}, a<x \leqslant m \\ \mu_A(x)=\frac{b-x}{b-m}, m<x \leqslant b \\ \mu_A(x)=0, x>b\end{array}\right., $ | (1) |
| $ A=\left[U_\lambda^l, U_\lambda^r\right]=[(m-a) \lambda+a, -(b-m) \lambda+b], $ | (2) |
| 三角模糊数A Triangular fuzzy number A |
λ-截集 λ-cut sets |
语言变量 Linguistic variables |
| (0.0,0.0,0.1) | [0.0, -0.1λ+0.1] | Very Low (VL) |
| (0.0,0.1,0.3) | [0.1λ+0.0, -0.2λ+0.3] | Low (L) |
| (0.1,0.3,0.5) | [0.2λ+0.1, -0.2λ+0.5] | Fairly Low (FL) |
| (0.3,0.5,0.7) | [0.2λ+0.3, -0.2λ+0.7] | Middle (M) |
| (0.5,0.7,0.9) | [0.2λ+0.5, -0.2λ+0.9] | Fairly High (FH) |
| (0.7,0.9,1.0) | [0.2λ+0.7, -0.1λ+1.0] | High (H) |
| (0.9,1.0,1.0) | [0.1λ+0.9, 1.0] | Very High (VH) |
其中,a和b分别表示模糊数的上界和下界,m表示可能性较大的值,λ表示集合μ的可信度。
2.2.2 语言变量的评价结果求解模糊数用于风险评估时,将语言变量作为专家分析各指标因素对事件影响的评价因子,由于领域专家的经验知识存在个体差异,为进一步克服主观意识的影响,利用全积分值法[30]对模糊数值解模糊化分析,解模糊原理如公式(3)所示。
| $I(A)=\alpha u_r(A)-(1-\alpha) u_l(A),$ | (3) |
其中,I表示解模糊化值,α表示乐观系数且α∈[0, 1]。当α取0或1时,表示A的上界或下界;α取0.5时,表示A解模糊化后的表示值。ul(A)和ur(A)分别表示A上下界隶属度函数的积分值,如公式(4)和公式(5)所示。
| $u_l(A)=\frac{1}{2}\left(\sum\limits_{\lambda=0.1}^1 A_l^\lambda \Delta \lambda+\sum\limits_{\lambda=0}^{0.9} A_l^\lambda \Delta \lambda\right),$ | (4) |
| $u_r(A)=\frac{1}{2}\left(\sum\limits_{\lambda=0.1}^1 A_r^\lambda \Delta \lambda+\sum\limits_{\lambda=0}^{0.9} A_r^\lambda \Delta \lambda\right),$ | (5) |
其中,λ=0, 0.1, 0.2, …, 1,且Δλ取值为0.1;Alλ和Arλ分别表示λ-截集的上下界。
2.3 基于词频-逆文档频率指标客观赋权原理TF-IDF算法是应用于搜索或在文本分类时关键词提取的一种技术[31],计算原理如公式(6)所示。当某个关键词在单个文档出现的频次越高,说明其区分文档内容特征的效果越好。相反,当该关键词所属语料库的文档数量越多时,其区分内容特征的能力越弱。
衡量群体性事件关键词引起暴恐转向风险的重要性时,关键词在单个文档的出现频次越高,并且其所属文档范围越广时,说明该关键词对群体性事件语料库的重要程度越高,同时表明内容对该关键词的依赖性越强。因此,将TF-IDF计算公式中的IDF加以改进,如公式(7)所示,将真数的分母改为文档总数D与关键词所在文档数之差,表达IDF值与关键词分布呈正比关系,并通过增加偏移量,避免差运算导致分母为0时引起结果异常,TF-IDF的计算方法如公式(8)所示。
| $t f_{i j} \_i d f_i=t f_{i j} \times i d f_i, t f_{i j}=\frac{N_{i j}}{\sum\nolimits_k^n N_{k j}},$ | (6) |
| $i d f_i^{\prime}=\log \left(\frac{|D|}{1+\left|D-\left\{j: i \in d_j\right\}\right|}\right),$ | (7) |
| $f_{i j}\_i d f_i^{\prime}=t f_{i j} \times i d f_i^{\prime},$ | (8) |
其中,tfij_idfi表示文档j中词i的词频-逆文档频值,tfij代表文档j中词i的词频,idfi表示词i的逆文档频率,Nij表示词i在文档j出现的次数,
博弈论是用于研究双方或多方在合作、冲突或决策场景下的理论方法,通过融合双方或多方分析结果来寻找问题的最优解,以满足彼此效益最大化目标[32]。因此,本文将博弈论思想应用于权衡群体性事件指标体系主、客观赋权法之间的差异,获得引发暴恐转向风险的最优指标权重。假设指标有k种赋权方法,存在不全为0的系数ε,将最终权重W表示为各计算方法求解权重的线性组合,如公式(9)所示,最小化目标函数如公式(10)所示。
| $W=\varepsilon_1 W_1+\varepsilon_2 W_2+\cdots+\varepsilon_k W_k,$ | (9) |
| $\min \left\|\sum\limits_{j=1}^k \varepsilon_j W_j^{\mathrm{T}}-W_j\right\|,$ | (10) |
其中,W表示组合权重,εj表示第j个赋权方法权重Wj的系数,j取1至k,且由于本次实验权重计算方法为2种,故k=2。
结合微分最优化求解性质,将目标函数转化为可以利用一阶导数求解的线性方程组合,如公式(11)所示,将求解出的系数εj利用公式(12)进行归一化处理,组合权重如公式(13)所示。
| $ {\left[\begin{array}{cccc}W_1 W_1^{\mathrm{T}} & W_1 W_2^{\mathrm{T}} & \cdots & W_1 W_k^{\mathrm{T}} \\ W_2 W_1^{\mathrm{T}} & W_2 W_2^{\mathrm{T}} & \cdots & W_2 W_k^{\mathrm{T}} \\ \vdots & \vdots & \vdots & \vdots \\ W_k W_1^{\mathrm{T}} & W_k W_2^{\mathrm{T}} & \cdots & W_k W_k^{\mathrm{T}}\end{array}\right] *\left[\begin{array}{c}\varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_k\end{array}\right]=} {\left[\begin{array}{c}W_1 W_1^{\mathrm{T}} \\ W_2 W_2^{\mathrm{T}} \\ \vdots \\ W_k W_k^{\mathrm{T}}\end{array}\right], }$ | (11) |
| $\varepsilon_j^{\prime}=\frac{\varepsilon_j}{\sum\nolimits_{j=1}^k \varepsilon_j},$ | (12) |
| $W^{\prime}=\sum\nolimits_{j=1}^k \varepsilon_j^{\prime} W_j^{\mathrm{T}},$ | (13) |
其中,W′表示k种赋权法的组合权重,εj′表示第j个赋权方法权重Wj的标准化系数,j取1至k,且k=2。
2.5 贝叶斯网络模型贝叶斯网络(BN)又称信念网络或有向无环图模型,用于描述数据表达不完全、模糊不确定场景的概率因果关系推理等[33]。如今群体性事件借助社交媒体迅速演变,利用基于概率的因果推理模型,可以增强发生预测暴恐转向风险的可解释性。BN基本单位称为父节点,输出结果称为目标节点,链接父节点和目标节点的称为中间节点,拓扑结构如图 1所示。

|
| 图 1 BN拓扑结构 Fig. 1 BN topology |
BN以贝叶斯理论为基础,利用先验概率和条件概率逐层推理目标节点概率的过程称为正向推理,而反向推理时则将目标节点发生状态值设置为100%,更新中间节点条件概率,利用父节点的输出概率对研究目标采取针对性优化措施。利用基于组合赋权计算的指标权重值,作为BN推理预测暴恐转向风险父节点的先验概率分布。对BN中任意随机变量v=(v1, v2, …, vn),联合概率密度分布如公式(14)所示,条件概率表达式如公式(15)所示。
| $P\left(v_1, v_2, \cdots, v_n\right)=\prod\limits_{i=1}^n P\left(v_i \mid v_1, v_2, \cdots, v_{i-1}\right),$ | (14) |
| $P\left(v_i \mid v_1, v_2, \cdots, v_{i-1}\right)=\frac{P\left(v_1, v_2, \cdots, v_i\right)}{P\left(v_1, v_2, \cdots, v_{i-1}\right)},$ | (15) |
其中,P(v1, v2, …, vn)表示联合概率密度分布,P(vi|v1, v2, …, vi-1)表示节点vi的条件概率,vi表示第i个节点,n为节点总数。
3 案例验证与结果分析 3.1 案例分析 3.1.1 背景描述2019年,中国香港部分群体因不满相关部门的某项决定,引发多起群体性事件,本文以其中的“7·21”事件为研究案例。事件组织者从2019年7月11日开始宣传造势,期间事件组织者通过社交媒体不断以推文、视频或直播的形式,持续推动群体情绪升温,煽动参与者以集会、游行和抗议的方式发泄不满。事件于2019年7月21日晚爆发,事件参与者行为逐渐转向极端的暴力化行动,当晚部分涉事者在地铁口手持武器袭击过往乘客,并对公共基础设施实行打砸破坏,情节极为恶劣,该起事件随即被相关部门列为恐怖主义性质的袭击事件。
3.1.2 数据采集本文以百度、微博、Twitter社交媒体平台以及问卷调查形式作为数据来源。百度指数是用于衡量和表征网民在线搜索行为的一种大数据指标,反映了网民在一定时间段内对事件的关注程度,通常将百度指数用于舆情趋势的研究[34]。Twitter是一种包含空间和时间信息的社交媒体平台,丰富的非结构化或半结构化数据构成了95%的社交大数据[35]。微博则与Twitter相似,汇集了大部分国内舆情数据。基于Python语言开发爬虫程序,获取事件期间至该起事件关注平息为止的搜索指数,从微博和Twitter平台爬取2019年7月11日至事件爆发前一天的数据,即截至2019年7月20日的总数量作为模型预测的数据集,共计149 327条文本信息,以小时划分区分文本数量,并对文本进行预处理工作。
利用Matlab软件绘制事件关注趋势曲线(图 2)。事件的关注趋势曲线显示,实际事件爆发后,网民对该事件仍存在一定程度的关注,甚至再次出现峰值点,说明该起群体性事件在第一次爆发后可能会引发衍生危害,如经济严重下滑或事件治理措施效果不佳等原因导致的二次事件。
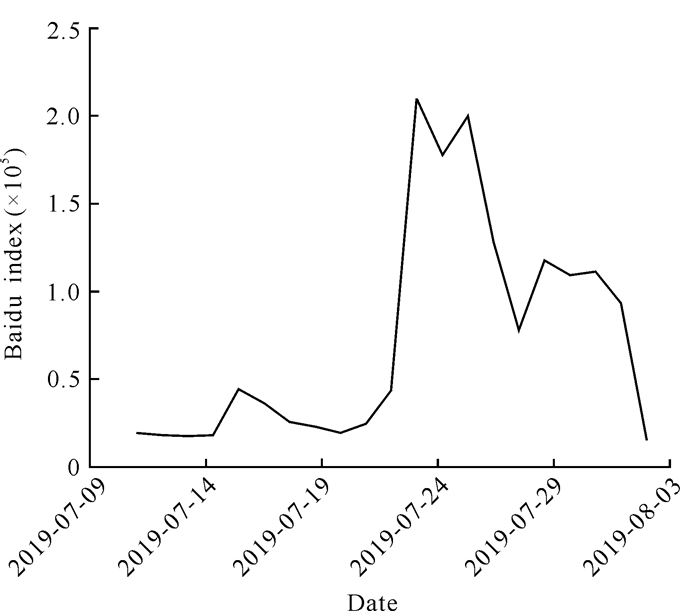
|
| 图 2 案例“7·21”事件的关注趋势 Fig. 2 Attention trend of case "7·21" |
为避免相关敏感信息引起误解,本实验展示的所有结果凡是涉及国外相关因素的均以“海外”代替,涉及相关部门信息的均以“部门”代替,出现的人员姓名均以“某”统一进行替换。
3.2 结果与分析 3.2.1 组合权重分析依据TF-IDF算法原理提取关键特征词的词频,并计算其权重。依据各类别特征词的词频大小由高到低排序,结合暴恐转向风险指标体系的二级指标划分特征词类别,分别截取出词频较高的代表性特征词,如表 3所示。根据表 3词频统计结果可知,对应指标B1交通枢纽、B2闹市区、C1法律因素和F1行为方式的相关词频明显较高。C1反映了触发事件活动的主题因素,F1显示事件爆发前存在集会、游行、罢工等活动,使用或将使用一些瓦斯、烟幕弹等工具,而且人员密集地出现频率最高,在一定程度上说明事件态势逐渐趋向暴力冲突。
| 二级指标 Secondary index |
特征词 Feature words |
特征词总数 Total number of feature words |
| A1:key dates | Anniversaries, weekends, memorial day | 5 046 |
| A2:duration time | All day, all night, morning | 2 482 |
| B1:transportation hub | School, railway station, subway station | 19 771 |
| B2:downtown area | Shopping malls, squares, blocks, sidewalks | 24 797 |
| B3:landmark building | Department | 4 692 |
| C1:legal factor | Regulations, laws, ordinances | 16 818 |
| C2:electoral factor | Take office | 10 195 |
| C3:rights protection | Human rights, freedom | 4 903 |
| D1:geographical scope | State, country | 3 210 |
| D2:number of participants | Hundreds, tens of thousands | 9 351 |
| E1:group organization | Network navy | 11 502 |
| E2:representative figure | Someone | 13 521 |
| F1:behavior | Protests, rallies, marches, gatherings | 21 851 |
| G1:overseas public opinion | Overseas | 2 705 |
| H1:weather | Cloudy | 467 |
| I1:economic level | Economy, fall, collapse | 12 396 |
| I2:local governance | Repression, control, tear gas, arrest | 10 095 |
主观权重计算中,选取54名公共安全研究领域人员组成专家评价小组,并说明此次调查问卷的目的和意义。随后对问卷结果进行收集、归纳整理,计算各指标主观权重,如A1指标权重,其中调查问卷中专家在A1关键日期对事件发生暴恐转向风险的影响评价结果分别为2VL、5L、3FL、13M、15FH、14H、2VH,将语言评价结果转化为表 2对应的λ-截集,根据公式(3)至(5)解模糊原理进行计算,计算过程如公式(16)所示。
| $\begin{array}{l} \qquad \mathrm{A} 1=\frac{1}{2} \times \frac{1}{54}((2 \times 0+0.1 \times 5+0.2 \times(3+ \\ 13+15+14)+0.1 \times 2+0.1 \times 3+0.3 \times 13+0.5 \times \\ 15+0.7 \times 14+0.9 \times 2)+(-0.1 \times(2+14)-0.2 \times \\ (5+3+13+15)+(0.1 \times 2+0.3 \times 5+0.5 \times 3+ \\ 0.7 \times 13+0.9 \times 15+14+2)))=0.61 。\end{array}$ | (16) |
基于博弈论原理公式(11)至(13)确定主、客观权重组合最优权值,组合指标权重结果如表 4所示。
| 二级指标 Secondary index |
主观权重 Subjective weight |
客观权重 Objective weight |
组合权重 Combined weight |
| A1:key dates | 0.61 | 0.37 | 0.48 |
| A2:duration | 0.60 | 0.18 | 0.36 |
| B1:transportation hub | 0.69 | 0.83 | 0.77 |
| B2:downtown area | 0.75 | 0.89 | 0.83 |
| B3:landmark building | 0.57 | 0.42 | 0.49 |
| C1:legal factor | 0.84 | 0.71 | 0.77 |
| C2:electoral factor | 0.69 | 0.56 | 0.62 |
| C3:rights protection | 0.74 | 0.32 | 0.51 |
| D1:geographical scope | 0.51 | 0.47 | 0.49 |
| D2:number of participants | 0.71 | 0.59 | 0.64 |
| E1:group organization | 0.73 | 0.84 | 0.79 |
| E2:representative figure | 0.72 | 0.79 | 0.76 |
| F1:behavior | 0.72 | 0.71 | 0.71 |
| G1:overseas public opinion | 0.26 | 0.77 | 0.55 |
| H1:weather | 0.66 | 0.81 | 0.74 |
| I1:economic level | 0.58 | 0.68 | 0.63 |
| I2:local governance | 0.54 | 0.74 | 0.65 |
3.2.2 暴恐转向风险预测结果分析
指标体系代表事件发生的可能诱导因素,在利用BN做因果分析时,将二级指标作为BN拓扑结构的父节点,一级指标作为中间节点,目标节点即为事件在演化过程中发生态势升级的暴恐转向概率。利用GENIE软件绘制BN拓扑结构模型,拓扑结构可视化界面中显示的State1状态表示该节点对事件发生起促进作用,State0状态则表示抑制作用。组合权重作为BN网络父节点的输入参数,结合BN原理预测目标节点的概率,结果如图 3所示。
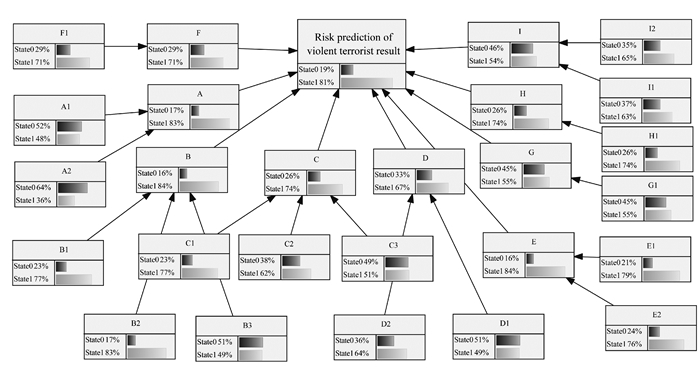
|
| 图 3 暴恐转向风险预测结果 Fig. 3 Risk prediction result of violent terrorist |
由暴恐转向风险预测结果可知,目标节点“暴恐转向风险”的预测概率高达81%,说明该事件在当时发生暴力化转向的风险程度非常高,且模型预测结果与2019年7月21日的真实情况总体一致,验证了基于组合赋权的暴恐转向风险预测模型对群体性事件态势预测的有效性,同时也体现了依据多角度分析事件影响因素构建的暴恐转向指标体系的可用性。
根据BN因果关系推理链,反向推理分析导致事件发生态势转变的形成原因与生成机理。反向推理过程即假设目标节点“暴恐转向风险”发生率为100%,逆向推出中间节点和父节点的后验概率,得到反向推理结果如图 4所示。
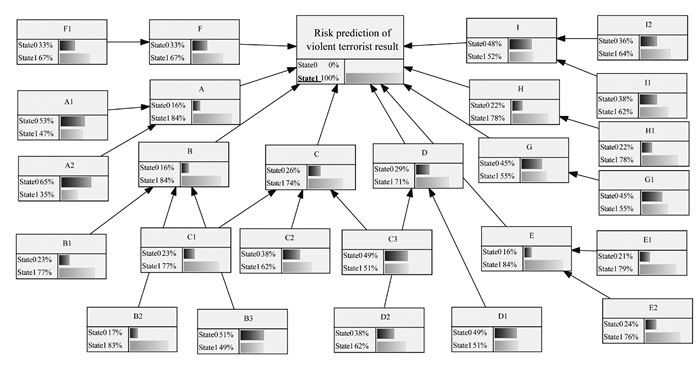
|
| 图 4 反向推理结果 Fig. 4 Result of reverse reasoning |
反向推理结果显示:①中间节点A事件时间、B事件地点、C事件主题、D事件规模的后验概率大于或等于70%,说明相应指标因素对事件发生暴恐转向的影响程度较深,相关部门在研究判断事件的风险时,需要重点关注上述影响因素。②父节点B1交通枢纽、B2闹市区、E1团体组织、E2代表人物和H1天气情况的后验概率均高于75%,充分表明在高密度人群活动场景下,如果同时伴随着社交媒体舆论的推动,事件更容易引发态势转变。而E1团体组织包含了涉事相关的媒体阵营和水军团体,媒体阵营利用网络平台宣传事件相关信息,带动话题热度,扩大事件传播范围。父节点E2代表人物在事件活动过程具有意见主导性作用,其通过社交媒体发文和直播等形式的煽动性更强,对事件趋势发生质变的影响作用更深。对于天气情况,如连续阴天或炎热天气可能会引起参与者出现不安、焦躁等情绪波动的现象,进一步推动事件态势演化。父节点G1的后验概率为55%,说明海外势力对诱发事件暴恐转向也具有一定程度的推动作用。③图 4中节点A1、A2、B3的State1状态值为30%-50%,表示该节点也是事件态势升级研究可依据的影响因素。
4 结论针对群体性事件在其态势演变过程中是否会发生暴恐转向,以及暴恐转向的发生风险程度预测问题,本文构建了基于组合赋权的暴恐转向风险预测模型。首先,通过考虑群体性事件自身的模糊性和不确定性,从多角度建立影响事件发生暴恐转向的指标体系,并阐述了各指标点的影响机理;其次,利用模糊理论对事件影响因素进行评估,将定性指标转化为确定量值,实现了指标评估由模糊到具体的过程;再次,考虑到定性分析存在的个体差异,采用积分值法与博弈论知识,在模糊量化过程中将主观意识进行多次模糊消解处理;然后,利用TF-IDF技术提取影响事件的高频词汇,从客观角度分析引发事件态势升级的主要因素;最后利用可解释性的贝叶斯网络模型实现因果推理,根据案例组合指标权重推理预测了事件发生暴恐转向风险的概率,其预测概率高达81%,与真实情况相比,预测结果表明了预测模型的有效性和合理性。
本文研究方法为群体性事件态势分析提供了一条新的研究思路,可为相关应急部门提前预警,争取提前布控或采取高效应急措施的时间,降低二次事件出现的可能,最大程度地减轻群众损失和降低社会危害。但本文研究方法仍存在一定的局限性:因果推理模型较为单一,数据处理过程相对较为复杂。因此,未来将在多类别数据集上采用多种模型推理预测进行对比研究分析,在充分挖掘数据信息的同时,简化数据处理过程,进一步提高模型的多场景适应性。
| [1] |
WANG X, WU C X. Design and implementation of virtual simulation platform for omni-media public opinion guidance[J]. Journal of Simulation, 2021, 9(1): 13-18. |
| [2] |
李鑫, 程静, 李慧波, 等. 基于大数据的典型社会安全事件预测预警技术研究[J]. 中国电子科学研究院学报, 2019, 14(5): 457-461. |
| [3] |
李倩倩, 王红兵, 刘怡君, 等. 我国群体性事件的典型特征、治理问题与对策建议[J]. 智库理论与实践, 2022, 7(2): 74-82. |
| [4] |
CHEN T G, SHI J W, YANG J J, et al. Modeling public opinion polarization in group behavior by integrating SIRS-based information diffusion process[J]. Complexity, 2020, 2020: 1-20. |
| [5] |
MA N, LIU Y J. SuperedgeRank algorithm and its application in identifying opinion leader of online public opinion supernetwork[J]. Expert Systems with Applications, 2014, 41(4): 1357-1368. DOI:10.1016/j.eswa.2013.08.033 |
| [6] |
BU F L, DANG H S, GAO M M. Study of individual's risk perception in collective violent events [C]//2014 IEEE International Conference on Progress in Informatics and Computing. Piscataway, NJ: IEEE, 2014: 139-143.
|
| [7] |
HUANG L D, CAI G, YUAN H Y, et al. From public gatherings to the burst of collective violence: an agent-based emotion contagion model [C]//2018 IEEE International Conference on Intelligence and Security Informatics. Piscataway, NJ: IEEE, 2018: 193-198.
|
| [8] |
丁雪枫. 情绪主导型群体事件的情绪演化模型与仿真[J]. 计算机工程与应用, 2018, 54(19): 230-236. |
| [9] |
GUSTAFSON D. Hunger to violence: explaining the violent escalation of nonviolent demonstrations[J]. Journal of Conflict Resolution, 2020, 64(6): 1121-1145. |
| [10] |
AN L, HAN Y X, YI X Y, et al. Prediction and evolution of the influence of microblog entries in the context of terrorist events[J]. Social Science Computer Review, 2021, 41(1): 1-19. |
| [11] |
许烨婧, 黄微, 郭苏琳, 等. 多媒体网络舆情话题衍进追踪态势及机理解析[J]. 情报理论与实践, 2020, 43(12): 156-162. |
| [12] |
安璐, 李倩. 基于热点主题识别的突发事件次生衍生事件探测[J]. 情报资料工作, 2020, 41(6): 26-35. |
| [13] |
李丽华, 韩思宁. 暴恐事件网络舆情传播机制及预防研究——英国典型案例的实证分析[J]. 情报杂志, 2019, 38(11): 102-111, 54. |
| [14] |
JIA M M, LI X Y, DU Y J, et al. An opinion evolution model based on the interaction behavior and influence of microblog users [C]//2019 2nd International Conference on Safety Produce Informatization. Piscataway, NJ: IEEE, 2019: 616-619.
|
| [15] |
DEB A, LUCERI L, BADAWY A, et al. Perils and challenges of social media and election manipulation analysis: the 2018 US midterms [C]//Companion Proceedings of the 2019 World Wide Web Conference. New York: ACM, 2019: 237-247.
|
| [16] |
CHEN Y Y, ZHENG W Z, LI W B, et al. Large group activity security risk assessment and risk early warning based on random forest algorithm[J]. Pattern Recognition Letters, 2021, 144: 1-5. |
| [17] |
WANG Q L. Research on security risk assessment mechanism of important event based on multi-source data[J]. Scientific Reports, 2022, 12(1): 4123. |
| [18] |
DUNCOMBE C. The politics of twitter: emotions and the power of social media[J]. International Political Sociology, 2019, 13(4): 409-429. |
| [19] |
陈磊, 陈世鸿, 刘宇, 等. 一种非常规突发事件演化的可计算模型[J]. 计算机工程与科学, 2011, 33(9): 63-69. |
| [20] |
WANG X F, WANG L, LI S J, et al. An event-driven plan recognition algorithm based on intuitionistic fuzzy theory[J]. The Journal of Supercomputing, 2018, 74(12): 6923-6938. |
| [21] |
WU J, OTA K, DONG M X, et al. Big data analysis-based security situational awareness for smart grid[J]. IEEE Transactions on Big Data, 2016, 4(3): 408-417. |
| [22] |
李锐. 风险评估研究方法综述[J]. 甘肃科技纵横, 2018, 47(9): 61-63. |
| [23] |
林焰, 杜锦涛, 黄紫林, 等. 基于多模块模糊贝叶斯网络的恐怖袭击事件量化分析[J]. 数学的实践与认识, 2019, 49(16): 157-172. |
| [24] |
王朝, 姚敏, 富展展. 基于模糊综合评价的突发事件分级研究[J]. 软件导刊, 2019, 18(4): 149-152. |
| [25] |
聂峰英, 张旸. 移动社交网络舆情预警指标体系构建[J]. 情报理论与实践, 2015, 38(12): 64-67. |
| [26] |
D'ETTORRE G, CAROLI A, PELLICANI V, et al. Preliminary risk assessment of workplace violence in hospital emergency departments[J]. Annali Di Igiene, 2020, 32(2): 99-108. |
| [27] |
ZADEH L A. The concept of a linguistic variable and its application to approximate reasoning-Ⅰ[J]. Information Sciences, 1975, 8(3): 199-249. |
| [28] |
WANG F. Preference degree of triangular fuzzy numbers and its application to multi-attribute group decision making[J]. Expert Systems with Applications, 2021, 178: 114982. |
| [29] |
NGUYEN H T. A note on the extension principle for fuzzy sets[J]. Journal of Mathematical Analysis and Applications, 1978, 64(2): 369-380. |
| [30] |
LIOU T S, WANG M J J. Ranking fuzzy numbers with integral value[J]. Fuzzy Sets and Systems, 1992, 50(3): 247-255. |
| [31] |
LIU C Z, SHENG Y X, WEI Z Q, et al. Research of text classification based on improved TF-IDF algorithm [C]//2018 IEEE International Conference of Intelligent Robotic and Control Engineering. Piscataway, NJ: IEEE, 2018: 218-222.
|
| [32] |
REN X M, JIANG Q H, JIANG J, et al. Evaluation of cabin energy consumption based on combination weighting and grey fuzzy comprehensive model[J]. EURASIP Journal on Advances in Signal Processing, 2022, 2022(1): 36. |
| [33] |
FENTON N, NEIL M. Risk assessment and decision analysis with Bayesian networks[M]. Boca Raton: CRC Press, 2018.
|
| [34] |
JI Q, YANG J, HE Q, et al. Understanding public attention towards the beautiful village initiative in China and exploring the influencing factors: an empirical analysis based on the Baidu index[J]. Land, 2021, 10(11): 1169. |
| [35] |
MARTÍN A, JULIÁN A B A, COS-GAYÓN F. Analysis of Twitter messages using big data tools to evaluate and locate the activity in the city of Valencia (Spain)[J]. Cities, 2019, 86: 37-50. |



