2. 广西医科大学, 广西南宁 530021
2. Guangxi Medical University, Nanning, Guangxi, 530021, China
当前社会经济有了巨大的发展,但人们出行时遇到的交通拥堵问题却日益严峻。政府、社会投入了大量资金,期望缓解交通拥堵,然而社会汽车保有量的增长速度远远快于道路建设速度,如何采用有效、科学的方案缓解交通拥堵,是当前人们面临的一个迫切问题[1]。在过去几十年里,研究者们从不同的角度提出了各种交通模型,如格子流体力学模型、元胞自动机模型、跟驰模型和耦合映射模型等[2-14]。在这些交通模型中,格子流体力学模型由于具有宏观离散性和计算的高效性,被人们广泛研究。1995年Bando等[15]提出了最优速度模型(OV模型),此后,许多学者对OV模型进行了改进研究,在原有模型中加入一些物理效应或交通因素等[3, 16]。Nagatani[17]在1998年首次提出了格子流体力学模型,该模型基于交通流流体动力学模型,从宏观上描述了连续车流之间的相互作用。运用非线性分析,得到在临界点附近的用mKdV方程描述的交通流拥堵和交通密度波的传播。1999年,Konishi等[18]在离散时间的OV模型的基础上,首次提出了耦合映射(CM)模型中的延迟反馈控制(DFC)方法,通过理论分析和数值模拟,说明上述方法对控制交通拥堵有抑制作用。基于Nagatani和Konishi等的工作,许多研究者考虑不同的重要交通情况和控制参数,提出了各种控制模型[19-25],如考虑向后看效应[26]、司机的延迟反应[27, 28]、密度差效应[29]、中断概率影响[11]、上坡和下坡道路[30]、基于非车道格子流体力学模型[31]等。此外,唐铁桥等[32]提出了改进的双车道格子流体力学模型。Ge等[27]考虑驾驶员的反应延迟,得到了格子流体力学模型中的依赖于时间的Ginzburg-Landau (TDGL)方程,揭示了交通拥挤与交通流相变之间的关系。Jin等[33]考虑延迟反馈控制,研究了OV模型中交通流的稳定性。此外,由于行人流和交通流具有许多共同的特征,Tian等[34]在Nagatani的二维交通流模型的基础上提出了一种二维双向行人流。Cen等[35]提出了考虑延迟时间连续累积效应的双向行人流的二维格子流体力学模型。2015年,Ge等[36]在格子流体力学模型中引入了t时刻格子位置j与j+1的流量差作为反馈增益。Redhu等[37]考虑向前看效应,提出了多相的格子流体力学模型。魏麒等[38]研究了斜坡道路考虑平均流量差预期效应的格子流体力学模型。本研究根据Nagatani的格子流体力学模型,考虑把下游平均优化车流量与当前延迟车流量之间的差作为抑制交通阻塞的反馈控制项,建立控制方程。利用线性稳定性分析和非线性分析,推导出稳定条件以及描述密度波的mKdV方程的解,通过数值模拟验证理论分析结果。通过加入反馈控制项,研究反馈增益大小与反应时间长短对交通流拥堵的抑制作用。
1 模型建立1998年Nagatani[17]首次提出了格子流体力学模型,方程描述如下。
连续性方程:
| $ \partial_t \rho_j+\rho_0\left(q_j-q_{j-1}\right)=0, $ | (1) |
动力学方程:
| $ \partial_t q_j=a \rho_0 V\left(\rho_{j+1}(t)\right)-a q_j, $ | (2) |
其中,下标j表示格子位置;qj=ρjvj代表j格子位置时的交通流量;ρj和vj分别表示t时刻在j格子位置处的交通密度和瞬时速度;ρ0为总的平均密度;参量a表示交通流敏感系数,是延迟时间τ的倒数;取交通流优化速度函数V(ρ)如下:
| $ V(\rho)=\frac{V_{\max }}{2}\left[\tanh \left(\frac{2}{\rho_0}-\frac{\rho}{\rho_0^2}-\frac{1}{\rho_c}\right)+\right.\left.\\ \tanh \left(\frac{1}{\rho_c}\right)\right],$ | (3) |
其中,Vmax和ρc分别表示最大速度和安全临界密度。该函数在ρ=ρc=ρ0处有一个上界和一个拐点。
在方程(2)中,j+1位置的最优流量与j位置的瞬时流量之差决定了j位置处交通流量的变化,表明交通流的流动变化由下游交通流量与当前位置流量来决定。所以,为了揭示下游车流对当前位置交通流演化的影响,在格子流体力学方程的基础上,把在反应时间内下游平均优化车流量与当前延迟车流量的差作为延迟反馈控制项,得到以下控制方程:
| $ \partial_t \rho_j+\rho_0\left(q_j-q_{j-1}\right)=0, $ | (4) |
| $ \begin{array}{r} \partial_t q_j(t)=a \rho_0 V\left(\rho_{j+1}(t)\right)-a q_j(t)+ \\ a \lambda\left[\frac{1}{t_d} \int t_{t-t_d} \rho_0 V\left(\rho_{j+1}(t)\right) d t-q_j\left(t-t_d\right)\right], \end{array} $ | (5) |
其中,td为反应时间,参数λ为延迟反馈增益。为了抑制交通拥堵的产生,在式(5)中考虑把下游最优车流量的平均累积效应与当前延迟车流量的差作为延迟反馈控制。当λ=0时,该模型与Nagatani的模型一致。
利用梯度积分公式对式(5)中的积分进行简化,并结合式(4)和式(5)消去瞬时速度,得到密度方程:
| $ \begin{array}{*{20}{l}} \;\;\;\;\;\;\;\;\partial_t^2 \rho_j(t)+a \partial_t \rho_j(t)+a \lambda \partial_t \rho_j\left(t-t_d\right)+ \\ a \rho_0^2 V\left[\rho_{j+1}(t)-\rho_j(t)\right]+\frac{1}{2} a \lambda \rho_0^2 V\left[\rho_{j+1}(t)-\rho_j(t)+\right. \\ \left.\rho_{j+1}\left(t-t_d\right)-\rho_j\left(t-t_d\right)\right]=0。\end{array} $ | (6) |
应用线性稳定性分析方法来研究稳态交通流在小扰动作用下的演化情况。在稳态时,交通流处于均匀的密度和流量,在小扰动[ρ*, q*]作用下,在均匀稳态附近增加一个微扰,即ρj=ρ*+ρj0; qj=q*+qj0,因此,方程(4)和(5)分别可改写为
| $ \partial_t \rho_{j+1}^0+\rho_0\left(q_{j+1}^0-q_j^0\right)=0 , $ | (7) |
| $ \begin{gathered} \partial_t q_j^0(t)=a \rho_0 V^{\prime} \rho_{j+1}^0(t)-a q_j^0(t)+ \\ \frac{1}{2} a \lambda \rho_0 V^{\prime}\left[\rho_{j+1}^0(t)-\rho_{j+1}^0\left(t-t_d\right)\right]-a \lambda q_j^0\left(t-t_d\right), \end{gathered} $ | (8) |
其中,
| $ s P_{j+1}(s)-\rho_{j+1}(0)+\rho_0\left(Q_{j+1}(s)-Q_j(s)\right)=0, $ | (9) |
| $ \begin{gathered} s Q_{j+1}(s)-q_j(s)=a \rho_0 V^{\prime} P_{j+1}(s)-a Q_j(s)+ \\ \frac{1}{2} a \lambda \rho_0 V^{\prime} P_{j+1}(s)\left(1+e^{-s t_d}\right)-a \lambda Q_j(s) e^{-s t_d}, \end{gathered} $ | (10) |
其中,L(ρj0)=P(s), L(qj0)=Q(s),
| $ \begin{array}{*{20}{l}} \;\;\;\;\;Q_j(s)=\left(\frac{-a \rho_0^2 V^{\prime}-\lambda a \rho_0^2 V^{\prime}+\frac{\lambda a \rho_0^2 V^{\prime} s t _d}{2}}{s^2-a \rho_0^2 V^{\prime}+a s-\frac{a \lambda \rho_0^2 V^{\prime}}{2}-\frac{\lambda a \rho_0^2 V^{\prime} e^{{-s t}_d}}{2}+a \lambda s e^{{-s t}_d}}\right) \\ Q_{j+1}(s)+\frac{a \rho_0^2 V^{\prime}+\frac{a \lambda \rho_0 V^{\prime}\left(2-s t_d\right)}{2}}{d s} \rho_{j+1}(0)+\frac{s}{d s} q_j(0) 。\end{array} $ | (11) |
因此,传递函数为
| $ G(s)=\frac{-a \rho_0^2 V^{\prime}-\lambda a \rho_0^2 V^{\prime}+\lambda a \rho_0^2 V^{\prime} s t_d / 2}{d s}, $ | (12) |
其中ds是特征多项式,
| $ \begin{aligned} & d s=s^2-a \rho_0^2 V^{\prime}+a s-a \lambda \rho_0^2 V^{\prime} / 2- \\ & \lambda a \rho_0^2 V^{\prime} e^{-s t_d} / 2+a \lambda s e^{-s t_d} 。\end{aligned} $ | (13) |
Konishi等[18, 39]基于控制理论得出关于交通拥堵的结论:如果满足以下两个条件,交通系统则不会发生拥堵, ①特征多项式ds是稳定的;②传递函数的H∞范数小于或等于1,即
根据Hurwitz稳定性准则,当ds大于零,特征多项式ds是稳定的[37]。对于方程(13),式中的每个系数都为正
| $ \begin{aligned} & |G(j w)|= \\ & \sqrt{\frac{\left(a \rho_0^2 V^{\prime}+a \lambda \rho_0^2 V^{\prime}\right)^2+\left(a \lambda \rho_0^2 V^{\prime} t_d w / 2\right)^2}{\left(w^2-a \lambda t_d w^2+a \rho_0^2 V^{\prime}+a \lambda \rho_0^2 V^{\prime}\right)^2+\left(a w+a \lambda w+a \lambda \rho_0^2 V^{\prime} t_d w / 2\right)^2}} \leqslant 1, \\ & w \in[0, \infty] 。\end{aligned} $ | (14) |
通过解方程(14),得稳定条件:
| $ a \geqslant-\frac{2 \rho_0^2 V^{\prime}}{1+\lambda-\lambda \rho_0^2 V^{\prime} t_d} 。$ | (15) |
显然,当λ=0,td=0,稳定条件与Nagatani模型的稳定条件(a≥-2ρ02V′)一致。
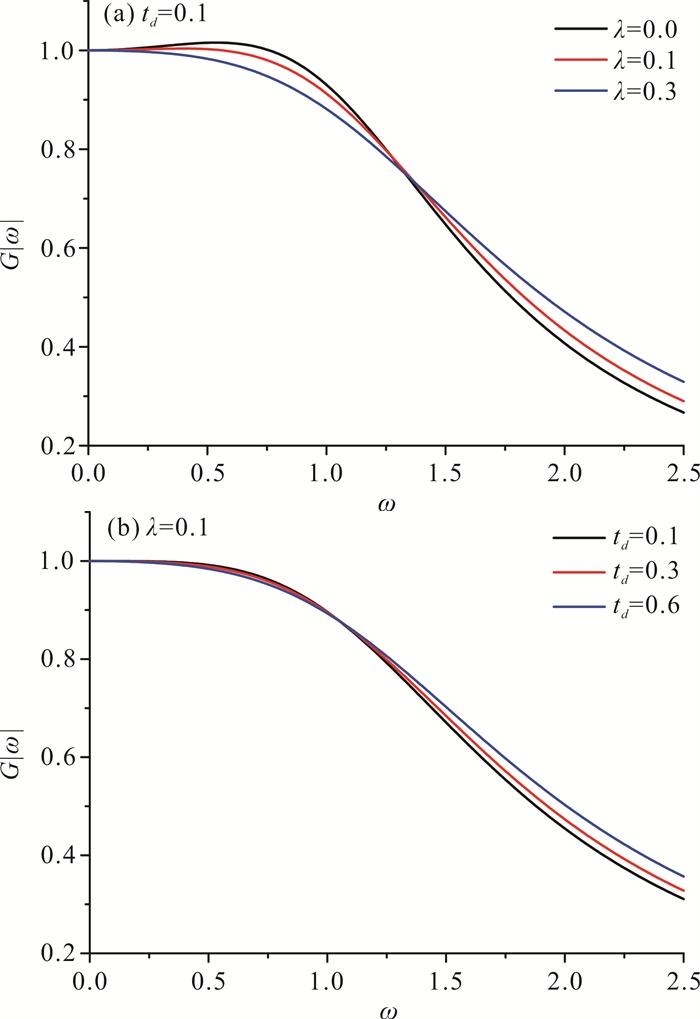
图 1反映了传递函数在不同反馈增益λ和反应时间td值的振幅变化。在图 1(a)中,反应时间td的值保持不变,改变反馈增益λ的值;而在图 1(b)中,反馈增益λ的值保持不变,改变反应时间td的值。从图 1可以看出,传递函数的幅值基本都小于1,说明增加反馈增益λ和反应时间td可以有效提高交通系统的稳定性。
|
| 图 1 不同反馈增益λ和反应时间td值的伯德图 Fig. 1 Bode-plot for different values of feedback gain λ and reaction time td |
3 非线性分析
为了研究在有限扰动作用下产生交通拥堵形成的密度波,采用非线性分析的约化摄动法研究在临界点附近交通密度波所满足的方程,并对方程进行求解。在临界点(ρc, ac)附近,对空间慢变量X和时间慢变量T作变换如下:
| $ X=\varepsilon(j+b t), T=\varepsilon^3 t, $ | (16) |
其中, j和t分别表示空间变量和时间变量;参数ε的取值范围为
| $ \rho_j(t)=\rho_c+\varepsilon R(X, T) 。$ | (17) |
将方程(16)和(17)代入密度方程(6)中,利用泰勒级数展开,展开到ε的五阶,得到非线性偏微分方程如下:
| $ \begin{aligned} & \quad \varepsilon^2\left\{a b(1+\lambda)+a \rho_c^2 V^{\prime}(1+\lambda)\right\} \partial_X R+\varepsilon^3\left\{b^2+\right. \\ & \left.\frac{1}{2} a \rho_c^2 V^{\prime}+\frac{1}{2} a \lambda \rho_c^2 V^{\prime}\left(1-b t_d\right)-a b^2 \lambda t_d\right\} \partial_X^2 R+ \\ & \varepsilon^4\left\{a(1+\lambda) \partial_T R+\frac{1}{6} a(1+\lambda) \rho_c^2 V^{\prime \prime \prime} \partial_X R^3+\left[\frac{1}{6} a(1+\right.\right. \\ & \left.\left.\lambda) \rho_c^2 V^{\prime}-\frac{1}{4} a \lambda \rho_c^2 V^{\prime} b t_d\right] \partial_X^3 R\right\}+\varepsilon^5\left\{\left[2 b-2 a \lambda b t_d-\right.\right. \\ & \left.\frac{1}{2} a \lambda \rho_c^2 V^{\prime} t_d\right] \partial_X \partial_T R+\left[\frac{1}{12} a(1+\lambda) \rho_c^2 V^{\prime \prime \prime}-\right. \\ & \left.\frac{1}{12} a \lambda \rho_c^2 V^{\prime \prime \prime} b t_d\right] \partial_X^2 R^3+\left[\frac{1}{24} a(1+\lambda) \rho_c^2 V^{\prime}-\right. \\ & \left.\left.\frac{1}{12} a \lambda \rho_c^2 V^{\prime} b t_d\right] \partial_X^4 R\right\}=0, \end{aligned} $ | (18) |
其中,
| $ \begin{aligned} & \;\;\;\;\varepsilon^4\left(\partial_T R-g_1 \partial_X^3 R+g_2 \partial_X R^3\right)+\varepsilon^5\left(g_3 \partial_X^2 R+\right. \\ & \left.g_4 \partial_X^4 R+g_5 \partial_X^2 R^3\right)=0, \end{aligned} $ | (19) |
| $ \begin{aligned} 其中, & g_1=-\frac{1}{1+\lambda}\left[\frac{1}{6}(1+\lambda) \rho_c^2 V^{\prime}-\frac{1}{4} \lambda \rho_c^2 V^{\prime} b t_d\right], \\ & g_2=\frac{1}{6} \rho_c^2 V^{\prime \prime \prime}, g_3=\frac{1}{a_c(1+\lambda)}\left(\rho_c^2 V^{\prime}\right)^2, \\ & g_4=\frac{1}{1+\lambda}\left[\frac{1}{24}(1+\lambda) \rho_c^2 V^{\prime}-\frac{1}{12} \lambda \rho_c^2 V^{\prime} b t_d\right], \\ & g_5=\frac{1}{1+\lambda}\left[\frac{1}{12}(1+\lambda) \rho_c^2 V-\frac{1}{12} \lambda \rho_c^2 V^{\prime \prime \prime} b t_d\right]。\end{aligned} $ |
为了得到标准的mKdV方程,采用以下变换:
| $ T^{\prime}=g_1 T, R=\sqrt{\frac{g_1}{g_2}} R^{\prime} 。$ | (20) |
因此,方程(19)可写为
| $ \partial_{T^{\prime}} R^{\prime}-\partial_X^3 R^{\prime}+\partial_X R^{\prime 3}+\varepsilon M\left[R^{\prime}\right]=0, $ | (21) |
其中,
| $ R_0^{\prime}\left(X, T^{\prime}\right)=\sqrt{c} \tanh \sqrt{\frac{c}{2}}\left(X-c T^{\prime}\right), $ | (22) |
其中R′0(X, T′)满足可解性条件:
| $ \begin{aligned} & \quad\left(R_0^{\prime}, M\left[R^{\prime}\right]\right)=\int_{-\infty}^{+\infty} \mathrm{d} X R_0^{\prime}\left(X, T^{\prime}\right) M[(X, \\ & \left.\left.T^{\prime}\right)\right] \text { 。} \end{aligned} $ | (23) |
通过积分化简,可得传播速度c的值:
| $ c=\frac{5 g_2 g_3}{2 g_2 g_4-3 g_1 g_5} 。$ | (24) |
因此,得到mKdV方程(20)的扭结-反扭结波的解为
| $ \rho_j=\rho_c+\varepsilon \sqrt{\frac{g_1 c}{g_2}} \tanh \left(\sqrt{\frac{c}{2}}\left(X-\operatorname{cg} g_1 T\right)\right) 。$ | (25) |
扭结-反扭结波的振幅A为
| $ A=\sqrt{\frac{g_1 c}{g_2}\left(\frac{a_c}{a}-1\right)} 。$ | (26) |
扭结-反扭结波的解代表低密度下的自由流和高密度下的堵塞相组成的共存相,其共存曲线可表示为
| $ \rho_j=\rho_c \pm A \text {, } $ | (27) |
其中, ρj=ρc-A表示交通阶段中的自由流;ρj=ρc+A表示交通阶段中的堵塞相。
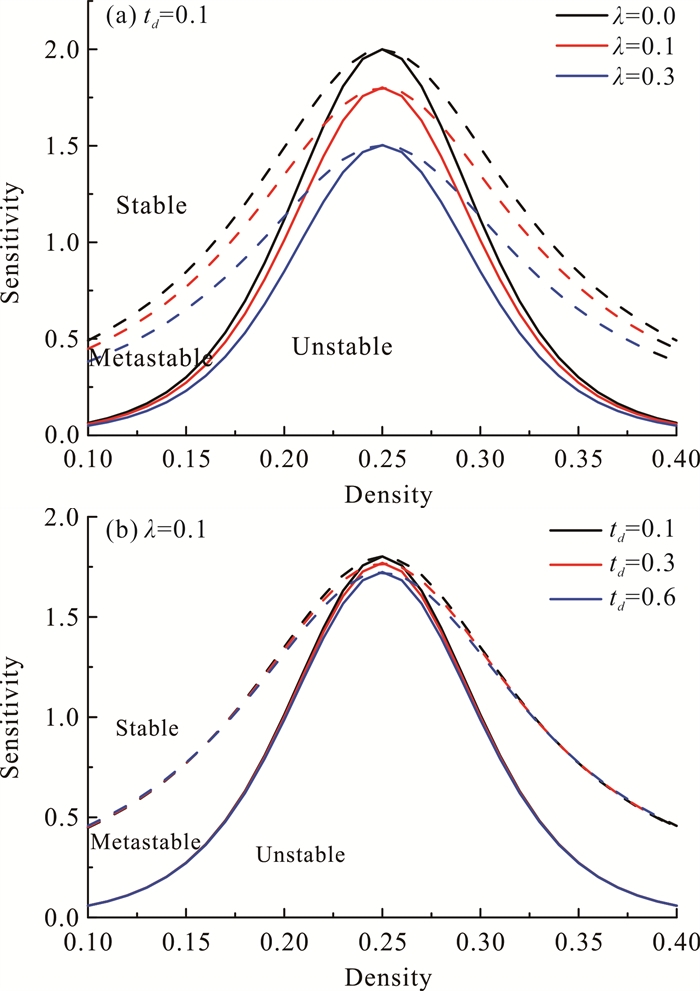
图 2为交通控制方程中密度敏感度(ρ, a)相图。每个图中都有3对曲线,实线为中性稳定线,虚线为共存曲线。根据交通流稳定性条件,将相图划分为3个区域:共存曲线以上的稳定区,中性稳定线以下的不稳定区,以及共存曲线与中性稳定线之间的亚稳定区。由图 2可以看出,中性稳定线和共存曲线随着反馈增益λ和反应时间td值的增加而下降,表明增加反馈增益λ和反应时间td可以有效地抑制交通拥堵产生。
|
| 图 2 密度敏感度(ρ, a)相图 Fig. 2 Phase diagrams of density sensitivity (ρ, a) |
4 数值模拟
采用周期边界条件进行数值模拟,验证线性稳定性分析和非线性分析的结论。为了便于模拟,对方程(6)应用差分方法进行离散,得到差分方程如下:
| $ \begin{array}{*{20}{l}} \;\;\;\;\;\rho_j(t+2 \Delta t)=2 \rho_j(t+\Delta t)-\rho_j(t)- \\ a \Delta t\left[\rho_j(t+\Delta t)-\rho_j(t)\right]-a \rho_0^2(\Delta t)^2\left[V\left(\rho_{j+1}(t)\right)-\right. \\ \left.V\left(\rho_j(t)\right)\right]-a \lambda \Delta t\left[\rho_j\left(t-t_d+\Delta t\right)-\rho_j\left(t-t_d\right)\right]- \\ \frac{1}{2} a \lambda \rho_0^2(\Delta t)^2\left[V\left(\rho_{j+1}(t)\right)-V\left(\rho_j(t)\right)+V\left(\rho_{j+1}(t-\right.\right. \\ \left.\left.\left.t_d\right)\right)-V\left(\rho_j\left(t-t_d\right)\right)\right] 。\end{array} $ | (28) |
数值模拟考虑道路离散格子单元数N=100,交通流初始状态均匀,密度为ρ0=ρc=0.25,敏感度系数a=1.65,最大速度Vmax=2,模拟的时间步长Δt=0.1,交通流的初始扰动设置为
| $ \rho_j(w)=\left\{\begin{array}{l} \rho_0 ; j \neq 50, 51 \\ \rho_0+0.1 ; j=50, \\ \rho_0-0.1 ; j=51 \end{array}\right. $ |
其中, w=1, 2, …, 5表示初始的5个时间步长。
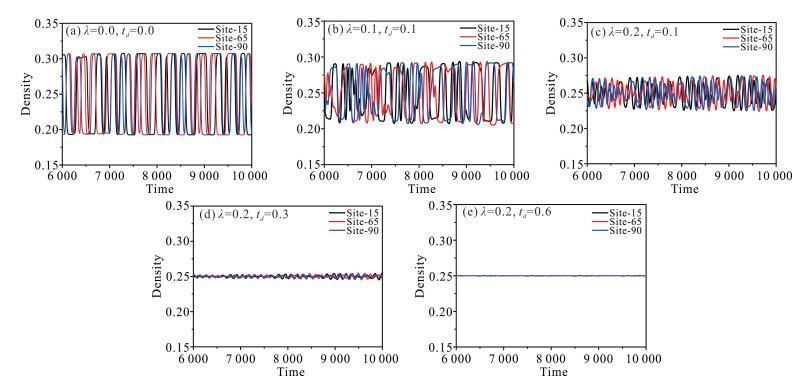
数值模拟结果如图 3、图 4和图 5所示。图 3显示了密度随时间变化的情况,从图中可以清楚地观察到扭结-反扭结密度波。在图 3(a)中,当反馈增益λ=0.0和反应时间td=0.0时,密度波的振幅急剧振荡。对比图 3(b)、(c)和对比图 3(c)、(d)、(e)可知,密度波振幅波动随反馈增益λ和反应时间td的增加而减小,有利于交通流的稳定。
|
| 图 3 不同反馈增益λ和反应时间td下的3个格点处的密度-时间图 Fig. 3 Density-time diagram at three lattice points under three feedback gain λ and reaction time td |
|
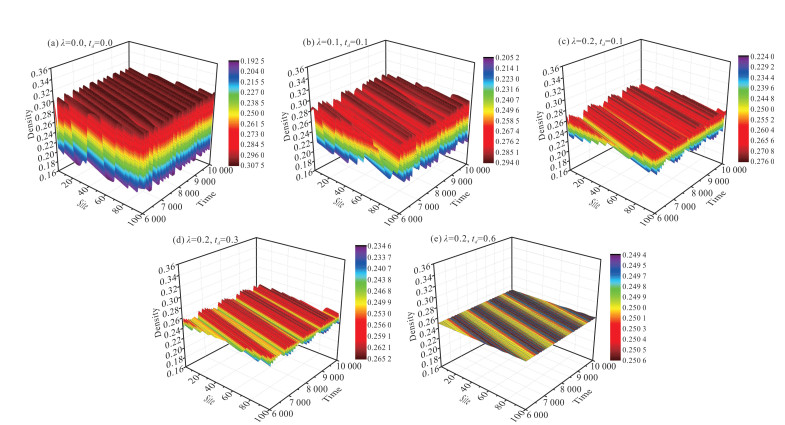
| 图 4 不同反馈增益λ和反应时间td下密度波的时空演化图 Fig. 4 Spatiotemporal evolution diagram of density wave under different feedback gain λ and reaction time td |
|
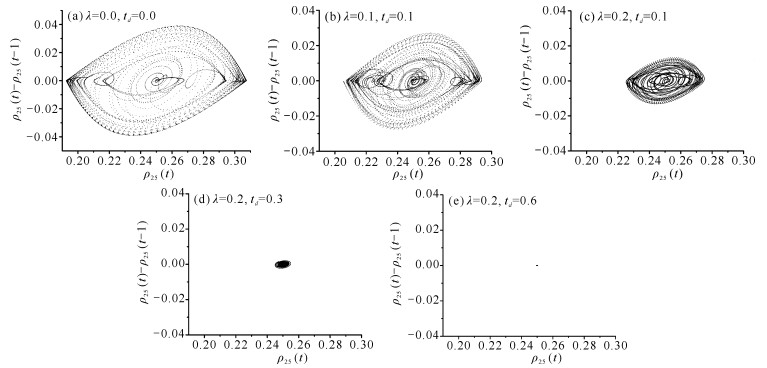
| 图 5 不同反馈增益λ和反应时间td在site-25处的散点图 Fig. 5 Scatter plot at site-25 under different feedback gain λ and reaction time td |
图 4为密度波的时空演化图。当不考虑反馈增益λ和反应时间td时,出现了扭结-反扭结的交通波现象,且波动幅度较大。当引入反馈增益λ和反应时间td时,密度波的波动减小。由于交通振荡的幅度与车辆系统的稳定性成正比,因此可知反馈增益λ和反应时间td的增加有利于车辆交通系统的稳定。
在不同反馈增益λ和反应时间td下,纵坐标为ρ25(t)-ρ25(t-1)与横坐标为ρ25(t)相空间密度差的散点图如图 5所示。在不考虑反馈增益λ和反应时间td的情况下,图 5(a)表现出明显的滞后现象和混沌行为,可以看出交通系统趋于不稳定。对比图 5(b)、(c)、(d)和(e)可知,随着反馈增益λ和反应时间td的增加,滞后曲线逐渐缩小。在图 5(e)中,滞后曲线缩小成一个点,说明交通拥堵得到了有效缓解。
5 结论本研究引入下游平均优化车流量与当前延迟车流量的差作为延迟反馈控制,提出了具有延迟反馈控制的交通流格子流体力学模型。通过线性稳定性分析,得到了传递函数和稳定条件;通过非线性分析得到了mKdV方程的扭结-反扭结密度波解。结果表明,反馈增益λ和反应时间td能有效缓解交通拥堵。为了验证理论分析,进行数值模拟,详细研究了在反馈控制作用下的密度-时间图和密度波的时空演化图。交通密度波的振荡减小表明反馈控制实现了抑制交通堵塞的控制策略。通过分析瞬时的交通密度差变化的散点图,发现在反馈增益λ=0时存在交通滞后和混沌现象。当加入反馈控制时,密度与密度差的空间散点图缩小为一个狭窄的有限区域,形成一个具有一定周期的极限环的稳态。交通滞后曲线的收缩表明交通系统的稳定性得到增强,有效地抑制了交通拥堵。仿真结果与理论分析结果一致,说明考虑下游平均优化车流量与当前延迟车流量的差作为反馈控制,有助于提高对交通系统的控制。
| [1] |
WANG T, ZANG R D, XU K Y, et al. Analysis of predictive effect on lattice hydrodynamic traffic flow model[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 526: 120711. DOI:10.1016/j.physa.2019.03.076 |
| [2] |
NAGATANI T. The physics of traffic jams[J]. Reports on Progress in Physics, 2002, 65: 1331-1386. DOI:10.1088/0034-4885/65/9/203 |
| [3] |
TANG T Q, LI C Y, HUANG H J. A new car-following model with the consideration of the driver's forecast effect[J]. Physics Letters A, 2010, 374: 3951-3956. DOI:10.1016/j.physleta.2010.07.062 |
| [4] |
JIANG C T, CHENG R J, GE H X. Mean-field flow difference model with consideration of on-ramp and off-ramp[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 513: 465-476. DOI:10.1016/j.physa.2018.09.026 |
| [5] |
TANG T Q, SHI W F, SHANG H Y, et al. An extended car-following model with consideration of the reliability of inter-vehicle communication[J]. Measurement, 2014, 58: 286-293. DOI:10.1016/j.measurement.2014.08.051 |
| [6] |
TANG T Q, HUANG H J, SHANG H Y. A new macro model for traffic flow with the consideration of the driver's forecast effect[J]. Physics Letters A, 2010, 374: 1668-1672. DOI:10.1016/j.physleta.2010.02.001 |
| [7] |
WANG Q Y, GE H X, CHENG R J. A new two-lane lattice hydrodynamic model considering the traffic interruption probability under honk environment[J]. Complexity, 2020, 2020: 1737318. |
| [8] |
TANG T Q, SHI W F, SHANG H Y, et al. A new car-following model with consideration of inter-vehicle communication[J]. Nonlinear Dynamics, 2014, 76: 2017-2023. DOI:10.1007/s11071-014-1265-9 |
| [9] |
JIANG R, HU M B, JIA B, et al. Spatiotemporal congested traffic patterns in macroscopic version of the Kerner-Klenov speed adaptation model[J]. Physics Letters A, 2007, 365: 6-9. DOI:10.1016/j.physleta.2006.12.058 |
| [10] |
GUPTA A K, REDHU P. Analyses of the driver's anticipation effect in a new lattice hydrodynamic traffic flow model with passing[J]. Nonlinear Dynamics, 2014, 76: 1001-1011. DOI:10.1007/s11071-013-1183-2 |
| [11] |
ZHANG Y, WANG S, PAN D B, et al. Stability analysis for a new lattice hydrodynamic model with time-varying delay in sensing traffic flux[J]. Physica A: Statistical Mechanics and Its Applications, 2021, 561: 125269. DOI:10.1016/j.physa.2020.125269 |
| [12] |
KAUR R, SHARMA S. Modeling and simulation of driver's anticipation effect in a two lane system on curved road with slope[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 499: 110-120. DOI:10.1016/j.physa.2017.12.101 |
| [13] |
REDHU P, GUPTA A K. Phase transition in a two-dimensional triangular flow with consideration of optimal current difference effect[J]. Nonlinear Dynamics, 2014, 78: 957-968. DOI:10.1007/s11071-014-1489-8 |
| [14] |
郭言, 施映, 章一才, 等. 考虑延迟效应的交通流宏观流体力学模型[J]. 广西科学, 2017, 24(4): 349-355. |
| [15] |
BANDO M, HASEBE K, NAKAYAMA A. Dynamical model of traffic congestion and numerical simulation[J]. Physical Review E, 1995, 51(2): 1035-1042. DOI:10.1103/PhysRevE.51.1035 |
| [16] |
TANG T Q, LI J G, YANG S C, et al. Effects of on-ramp on the fuel consumption of the vehicles on the main road under car-following model[J]. Physica A: Statistical Mechanics and Its Applications, 2015, 419: 293-300. DOI:10.1016/j.physa.2014.10.051 |
| [17] |
NAGATANI T. Modified KdV equation for jamming transition in the continuum models of traffic[J]. Physica A: Statistical Mechanics and Its Applications, 1998, 261: 599-607. DOI:10.1016/S0378-4371(98)00347-1 |
| [18] |
KONISHI K, KOKAME H, HIRATA K. Coupled map car-following model and its delay-feedback control[J]. Physical Review E, 1999, 60(4): 4000-4007. DOI:10.1103/PhysRevE.60.4000 |
| [19] |
WANG Y N, CHENG R J, GE H X. A lattice hydrodynamic model based on delayed feedback control considering the effect of flow rate difference[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 479: 478-484. DOI:10.1016/j.physa.2017.03.027 |
| [20] |
PENG G H, YANG S H, ZHAO H Z. New feedback control model in the lattice hydrodynamic model considering the historic optimal velocity difference effect[J]. Communications in Theoretical Physics, 2018, 70(6): 803-807. DOI:10.1088/0253-6102/70/6/803 |
| [21] |
ZHANG G, SUN D H, LIU H, et al. Stability analysis of a new lattice hydrodynamic model by considering lattice's self-anticipative density effect[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 486: 806-813. DOI:10.1016/j.physa.2017.05.050 |
| [22] |
PENG G H, KUANG H, QING L. Feedback control method in lattice hydrodynamic model under honk environment[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 509: 651-656. DOI:10.1016/j.physa.2018.06.080 |
| [23] |
PENG G H, YANG S H, ZHAO H Z. A delayed-feedback control method for the lattice hydrodynamic model caused by the historic density difference effect[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 509: 855-860. DOI:10.1016/j.physa.2018.06.097 |
| [24] |
CEN B L, XUE Y, ZHANG Y C, et al. A feedback control method with consideration of the next-nearest-neighbor interactions in a lattice hydrodynamic model[J]. Physica A: Statistical Mechanics and Its Applications, 2020, 559: 125055. DOI:10.1016/j.physa.2020.125055 |
| [25] |
TIAN J F, YUAN Z Z, JIA B, et al. The stabilization effect of the density difference in the modified lattice hydrodynamic model of traffic flow[J]. Physica A: Statistical Mechanics and Its Applications, 2012, 391(19): 4476-4482. DOI:10.1016/j.physa.2012.04.027 |
| [26] |
GE H X, CHENG R J. The "ackward looking" effect in the lattice hydrodynamic model[J]. Physica A: Statistical Mechanics and Its Applications, 2008, 387: 6952-6958. DOI:10.1016/j.physa.2008.05.060 |
| [27] |
GE H X, ZHENG P J, LO S M, et al. TDGL equation in lattice hydrodynamic model considering driver's physical delay[J]. Nonlinear Dynamics, 2014, 76: 441-445. DOI:10.1007/s11071-013-1137-8 |
| [28] |
KANG Y R, SUN D H. Lattice hydrodynamic traffic flow model with explicit drivers' physical delay[J]. Nonlinear Dynamics, 2013, 71: 531-537. DOI:10.1007/s11071-012-0679-5 |
| [29] |
WANG T, GAO Z Y, ZHANG J. Stabilization effect of multiple density difference in the lattice hydrodynamic model[J]. Nonlinear Dynamics, 2013, 73(4): 2197-2205. DOI:10.1007/s11071-013-0934-4 |
| [30] |
GUPTA A K, SHARMA S, REDHU P. Analyses of lattice traffic flow model on a gradient highway[J]. Communications in Theoretical Physics, 2014, 62(3): 393-404. DOI:10.1088/0253-6102/62/3/17 |
| [31] |
PENG G H, CAI X H, CAO B F, et al. Non-lane-based lattice hydrodynamic model of traffic flow considering the lateral effects of the lane width[J]. Physics Letters A, 2011, 375: 2823-2827. DOI:10.1016/j.physleta.2011.06.021 |
| [32] |
唐铁桥, 黄海军, 薛郁. 一种改进的两车道交通流格子模型[J]. 物理学报, 2006, 55(8): 4026-4031. |
| [33] |
JIN Y F, HU H Y. Stabilization of traffic flow in optimal velocity model via delayed-feedback control[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(4): 1027-1034. DOI:10.1016/j.cnsns.2012.08.031 |
| [34] |
TIAN H H, HE H D, WEI Y F, et al. Lattice hydrodynamic model with bidirectional pedestrian flow[J]. Physica A: Statistical Mechanics and Its Applications, 2009, 388(14): 2895-2902. DOI:10.1016/j.physa.2009.02.047 |
| [35] |
CEN B L, XUE Y, WANG X, et al. A lattice hydrodynamic model of bidirectional pedestrian traffic considering the cumulative effect of delay time[J]. IEEE Access, 2019(7): 168710-168719. |
| [36] |
GE H X, CUI Y, ZHU K Q, et al. The control method for the lattice hydrodynamic model[J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 22: 903-908. DOI:10.1016/j.cnsns.2014.09.014 |
| [37] |
REDHU P, GUPTA A K. Effect of forward looking sites on a multi-phase lattice hydrodynamic model[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 445: 150-160. |
| [38] |
魏麒, 常银银, 葛红霞, 等. 斜坡道路考虑平均流量差预期效应的格子流体力学模型[J]. 上海大学学报(自然科学版), 2020, 26(3): 367-381. |
| [39] |
KONISHI K, KOKAME H, HIRATA K. Decentralized delayed-feedback control of an optimal velocity traffic model[J]. The European Physical Journal B, 2000, 15(4): 715-722. |



