2. 南宁师范大学, 北部湾环境演变与资源利用教育部重点实验室,广西南宁 530001;
3. 中国科学院华南植物园,广东广州 510650
2. Key Laboratory of Environment Change and Resources Use in Beibu Gulf, Nanning Normal University, Ministry of Education, Nanning, Guangxi, 530001, China;
3. South China Botanical Garden, Chinese Academy of Sciences, Guangzhou, Guangdong, 510650, China
参考作物蒸散发(Reference Evapotranspiration,ET0)是水资源管理、灌溉制度设计以及水文模型的重要参数,反映了与下垫面(植被类型、地形及土壤水分等)无关的、在给定位置和时间的最大大气蒸发能力[1, 2]。联合国粮食及农业组织(FAO)推荐采用基于空气动力学及能量平衡原理建立的Penman-Monteith模型(FAO-56 P-M)作为ET0计算的标准方法,该模型还可用于校正其他ET0计算模型。然而FAO-56 P-M模型需要较完备的气象数据(太阳辐射、气温、风速和相对湿度),以及纬度和海拔高度,即使在发达国家,能同时测量这些气象数据的气象站点也很有限,而且FAO-56 P-M模型对数据质量有严格要求。如在全球范围内,大多数气象站均配备有气温传感器[3],但其他气象变量,特别是太阳辐射,仅有少数气象站点能够监测[3-5],所以FAO-56 P-M模型的应用受到一定的限制。另外,FAO-56 P-M模型在计算过程中需要计算很多中间参数,计算量大且烦琐[5, 6]。因此,使用气象因子较少、形式简单且具有足够精度的ET0计算模型(如Hargreaves、Priestley-Taylor、Ravazzani、Tralkovic、Makkink-Hansen、Oudin和Turc等经验模型)受到较多关注。学者们对这些经验模型在各地的适用性进行了检验及校正。如Gao等[4]评估了Hargreaves模型(需日平均气温、最高气温和最低气温)和McCloud模型(需平均气温)在贵州的适用性,并进行了校正,校正后的模型可替代FAO-56 P-M模型。Djaman等[7]分析了16个ET0计算模型在Senegal河谷的适用性,发现Hargreaves、修正的Hargreaves、Ravazzani和Tralkovic模型高估了ET0,而Makkink-Hansen、Oudin和Turc模型则低估了ET0,总体来看Valiantzas、Trabert、Romanenko、Schendel和Mahringer模型精度较高,在该地区可代替FAO-56 P-M模型。随着大数据时代的来临以及计算能力的进步,不少机器学习方法被用于ET0计算研究[1, 5, 6, 8],然而其得到的为黑箱模型,没有明确的算术表达式,不便于灌溉人员应用[9],且通用性较弱[1],也不能进行气象因子敏感性分析[10]。
与以上纯经验模型方法不同,Valiantzas[11]利用全球2 000个气象站点的气象数据,基于数值模拟及数理统计方法,将FAO-56 P-M模型中一系列中间参数用气象因子(输入变量)的算术表达式表示,从而建立了不同气象参数缺失下FAO-56 P-M的简化模型(下文简称Valiantzas模型)。相比于FAO-56 P-M模型,Valiantzas模型更直观、易用,计算更简便,且便于进行气象因子的敏感性分析,通用性更强,在一些地区发现其计算精度与FAO-56 P-M模型相当[12]。在Uganda湿润气候区的研究发现,缺少相对湿度数据的Valiantzas模型表现良好[13],而缺少风速数据的Valiantzas模型由于使用了世界平均风速值替代,导致估算的ET0误差较大。在伊朗的研究发现,Valiantzas模型最适用的气象条件为太阳净辐射大于24.2 MJ/(m2·d), 气温为16-18℃,相对湿度为40%-50%,风速为1.50-2.50 m/s[14]。
广西喀斯特地貌发育,因此,尽管该地区降雨充沛,但是由于特殊的地质背景(碳酸盐岩分布范围广),水文过程迅速[3],地表水缺乏。准确估算ET0是水资源合理分配与管理的基础。广西面临着气象站点稀疏及气象因子不完备等问题,且ET0在广西喀斯特与非喀斯特地区具有不同的年际变化特征和影响因子[15]。本研究通过检验Valiantzas模型在广西喀斯特与非喀斯特地区的适用性,并对相关模型进行校正,旨在为该地区农业水资源高效利用提供科学依据。
1 材料与方法 1.1 研究区概况与数据来源广西位于华南地区(104°26′-112°04′ E,20°54′-26°23′ N),地处中国地势第二阶梯中的云贵高原东南边缘,两广丘陵西部,地势西北高、东南低,呈现西北向东南倾斜趋势。陆地面积2.376×105 km2,碳酸盐岩面积约占广西陆地总面积的33.9%。广西属亚热带和热带季风气候,年平均气温为17.5-23.5℃,年平均降水量为841.2-3 387.5 mm。
本研究依据广西地形地貌,选取10个气象站点(5个为喀斯特站点,5个为非喀斯特站点[15]),共5年半(2010年1月-2015年6月)的逐日气象数据(来源于中国气象数据网http://data.cma.cn/),包括日照时数n(h)、最高气温Tmax(℃)、最低气温Tmin(℃)、平均气温T(℃)、平均相对湿度RH、距地面2 m高处风速u2(m/s)。各站点位置及气象因子平均值如表 1所示。
| 地貌类型 Geomorphic type |
站点 Stations |
纬度(°) Latitude (°) |
经度(°) Longitude (°) |
海拔(m) Altidude (m) |
降水量(mm) Rainfall (mm) |
气温(℃) Temperature (℃) |
风速(m/s) Wind speed (m/s) |
相对湿度(%) Relative humidity (%) |
日照时数(h) Sunshine duration (h) |
| Karst | Liuzhou | 24.35 | 109.40 | 96.8 | 1 528.5 | 21.6 | 1.1 | 71.5 | 1 315.5 |
| Du′an | 23.93 | 108.10 | 170.8 | 1 784.8 | 21.6 | 2.6 | 75.8 | 1 380.0 | |
| Fengshan | 24.55 | 107.03 | 484.6 | 1 564.0 | 20.3 | 0.9 | 77.4 | 1 203.2 | |
| Rong′an | 25.22 | 109.40 | 121.3 | 1 942.5 | 20.2 | 0.9 | 76.8 | 1 335.0 | |
| Guilin | 25.32 | 110.30 | 164.4 | 1 900.0 | 20.1 | 1.5 | 71.6 | 1 372.2 | |
| Non-karst | Mengshan | 24.20 | 110.52 | 145.7 | 1 738.0 | 20.8 | 1.2 | 76.9 | 1 373.1 |
| Hexian | 24.42 | 111.53 | 108.8 | 1 550.3 | 20.8 | 1.4 | 74.8 | 1 417.3 | |
| Baise | 23.90 | 106.60 | 173.5 | 1 066.8 | 22.1 | 1.5 | 72.5 | 1 543.1 | |
| Nanning | 22.63 | 108.22 | 121.6 | 1 304.2 | 22.2 | 1.2 | 79.2 | 1 667.1 | |
| Beihai | 21.45 | 109.13 | 12.8 | 1 670.0 | 23.5 | 2.1 | 79.0 | 1 750.0 |
1.2 ET0计算模型
采用表 2中的模型对ET0进行模拟计算。其中,太阳净辐射值由日照时数、地理纬度及日序数按经验公式求得。Valiantzas-M1-Valiantzas-M5为不同气象因子缺失下的Valiantzas简化模型[11, 12],Turk[16]、Makkink[5]、Priestley-Taylor和Irmark-Allen为常用的经验模型。
| 模型 Model |
表达式 Equations |
所需气象因子 The required meteorological factors |
| FAO-56 P-M | Tmax,Tmin,n,RH,u2 | |
| Valiantzas-M1 | Tmax,Tmin,n,RH,u2 | |
| Valiantzas-M2 | Tmax,Tmin,n,RH | |
| Valiantzas-M2- modify | Tmax,Tmin,n,RH | |
| Valiantzas-M3 | Tmax,Tmin,RH | |
| Valiantzas-M4 | Tmax,Tmin,n,RH | |
| Valiantzas-M5 | Tmax,Tmin,n | |
| Turk | Tmax,Tmin,n,RH | |
| Makkink | Tmax,Tmin,n | |
| Priestley-Taylor | Tmax,Tmin,n | |
| Irmark-Allen | ET0=0.480+0.289Rn+0.023 | Tmax,Tmin,n |
表 2中,Δ为饱和水汽压-气温关系曲线在平均气温T处切线的斜率(kPa/℃),γ为干湿计常数(kPa/℃),λ为水的汽化潜热(MJ/kg),G为土壤热通量[MJ/(m2·d)],Tmax、Tmin和T分别为最高、最低和平均气温(℃),TR=Tmax-Tmin(℃),Tdew为露点温度(℃),α为常数0.23,RS为太阳辐射[MJ/(m2·d)],Ra为大气顶层辐射[MJ/(m2·d)],Rn为太阳净辐射[MJ/(m2·d)],RH为平均相对湿度(%),u2为距地面2 m高度处风速(m/s),Z为气象站海拔高度(m),φ为纬度(rad)。Valiantzas-M4中,RH>50%时,Cu=0.076-0.0119(RH-50)0.2;RH≤50%时,Cu=0.076+0.0084(50-RH)0.2。Turk模型中,RH≤50%时,WRH取1;RH>50%时,WRH取0。
1.3 评价指标本研究采用5种常用的统计指标:Kling-Gupta Efficiency系数(KGE)、Nash效率系数(NSE)、决定系数(R2)、均方根误差(RMSE)以及平均偏差(PBIAS),计算公式如下:
| $ \mathrm{KGE}=1-\sqrt{(r-1)^2+(\alpha-1)^2+(\beta-1)^2}, $ | (1) |
| $ \mathrm{NSE}=1-\frac{\sum\nolimits_{i=1}^N\left(P_i-Q_i\right)^2}{\sum\nolimits_{i=1}^N\left(\bar{P}-Q_i\right)^2}, $ | (2) |
| $ R^2=\left[\frac{\sum\nolimits_{i=1}^N\left(O_i-\bar{O}\right) \sum\nolimits_{i=1}^N\left(P_i-\bar{P}\right)}{\sqrt{\sum\nolimits_{i=1}^N\left(O_i-\bar{O}\right)^2 \sum\nolimits_{i=1}^N\left(P_i-\bar{P}\right)^2}}\right]^2, $ | (3) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\nolimits_{i=1}^N\left(O_i-P_i\right)^2}, $ | (4) |
| $ \text { PBIAS }=100 \frac{\sum\nolimits_{i=1}^N\left(O_i-P_i\right)}{\sum\nolimits_{i=1}^N O_i} \times 100 \%, $ | (5) |
式中:N为样本数;Oi为FAO-56 P-M模型计算的标准值,O为其平均值;Pi为模型的模拟值,P为模型的平均值;r、α和β分别为标准值和模拟值的线性相关系数、方差之比和均值之比。NSE为(-∞, 1],用于评价模型模拟的好坏;KGE为(-∞, 1],作为NSE的补充,能弥补NSE对峰值敏感,对低值反应迟钝的缺陷[17];R2为(0, 1];RMSE越小,表明模型模拟误差越小;PBIAS为正,表明模型低估了目标值,反之亦然。KGE和NSE用R语言mbr包计算。
2 结果与分析 2.1 Valiantzas模型在喀斯特地区的适用性表 3给出了喀斯特5个站点在不同气象因子缺失情况下,5个Valiantzas模型(含1个修正的模型)与FAO-56 P-M模型模拟ET0精度对比情况。Valiantzas-M1模型与FAO-56 P-M模型所需气象因子相同,使用了所有的气象数据,具有较高的KGE(0.735)、NSE (0.841)和R2(0.969),以及最小的误差(RMSE和PBIAS分别为0.557 mm/d和-40.785%),因此其能更稳健地模拟ET0。
| Valiantzas模型 Valiantzas models |
输入气象因子 Input meteorological factors |
缺失气象因子 Missing meteorological factors |
KGE | NSE | R2 | RMSE (mm/d) | PBIAS (%) |
| Valiantzas-M1 | Tmax,Tmin,n,RH,u2 | — | 0.735 | 0.841 | 0.969 | 0.557 | -40.785 |
| Valiantzas-M2 | Tmax,Tmin,n,RH | u2 | 0.667 | 0.718 | 0.977 | 0.776 | -65.119 |
| Valiantzas-M2-modify | Tmax,Tmin,n,RH | u2 | 0.733 | 0.837 | 0.978 | 0.563 | -43.460 |
| Valiantzas-M3 | Tmax,Tmin,RH | n,u2 | 0.673 | 0.454 | 0.858 | 0.991 | -83.805 |
| Valiantzas-M4 | Tmax,Tmin,n,RH | u2 | 0.665 | 0.732 | 0.978 | 0.765 | -62.921 |
| Valiantzas-M5 | Tmax,Tmin,n | RH,u2 | 0.701 | 0.814 | 0.952 | 0.632 | -42.211 |
| Note: "-" represents no missing date | |||||||
Valiantzas-M2模型为原始缺失风速的模型(用2.00 m/s的世界平均风速来代替),Valiantzas-M2-modify模型为基于广西10个站点的平均风速(1.34 m/s)修正的Valiantzas-M2模型。由表 3可见,基于Valiantzas-M2-modify得到的ET0精度得到了提高,R2变化较小,KGE和NSE分别提高了9.9%和16.6%,RMSE和PBIAS分别降低了27.4%和33.3%。表明广西平均风速小于世界平均风速(2.00 m/s),用广西平均风速对Valiantzas-M2模型校正后能显著提高ET0模拟效果。
Valiantzas-M3模型为缺失太阳辐射和风速的模型,其模拟精度最低。这可能是因为太阳辐射和风速是该区域ET0最主要的两个影响因素[1],同时缺失这两个气象因子导致ET0模拟出现较大误差。
Valiantzas-M4模型也是缺失风速情况下的ET0计算模型,主要适用于湿润地区[12],其假定相对湿度较高时,空气动力项对ET0的影响较小,反之亦然。据此引入依赖于相对湿度的调节系数waero,应用于风速缺失情况。从NSE、RMSE和PBIAS来看,Valiantzas-M4模型优于Valiantzas-M2模型,NSE提高了1.9%,RMSE和PBIAS分别降低了1.4%和3.4%,表明在湿润地区缺失风速情况下,Valiantzas-M4模型比Valiantzas-M2模型更适用。
Valiantzas-M5模型是相对湿度和风速缺失下的FAO-56 P-M简化模型,通过建立相对湿度与气温的回归关系并结合Valiantzas-M1模型得到,具有足够高的精度。
由图 1可见,FAO-56 P-M模型与Valiantzas系列模型计算的ET0值在年内的变化趋势较一致,均呈“几”字形分布。各个模型计算的ET0值均在8月最大,分别为114.9 mm、136.8 mm、147.1 mm、139.2 mm、145.0 mm、146.6 mm和142.3 mm;在1月最小,分别为41.9 mm、43.7 mm、49.4 mm、44.2 mm、52.4 mm、49.2 mm和42.1 mm。Valiantzas系列模型均高估了各个月的ET0值,Valiantzas-M1、Valiantzas-M2、Valiantzas-M2-modify、Valiantzas-M3、Valiantzas-M4和Valiantzas-M5分别高估了16.8%、26.8%、17.9%、33.8%、25.9%和17.6%,可见Valiantzas-M1和Valiantzas-M5模型模拟的ET0值与FAO-56 P-M最接近。
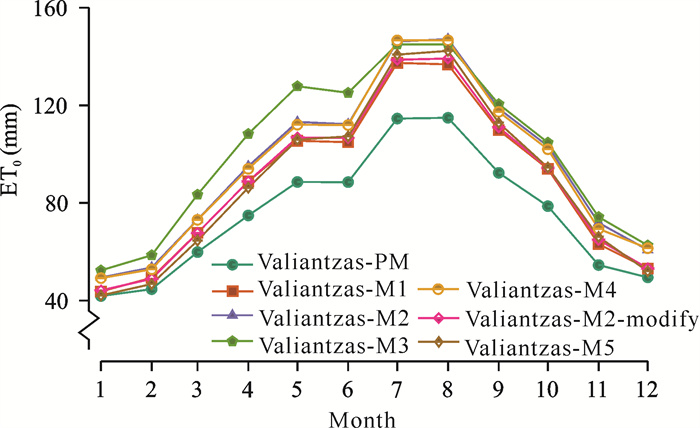
|
| 图 1 2010/1-2015/6喀斯特地区FAO-56 P-M模型与Valiantzas模型模拟ET0的各月均值 Fig. 1 Monthly average value of ET0 stimulated by FAO-56 P-M model and Valiantzas models in karst area during Jan, 2010 to Jun, 2015 |
2.2 Valiantzas模型在非喀斯特地区的适用性
表 4为不同气象因子缺失下Valiantzas模型在非喀斯特地区的计算精度。Valiantzas-M1模型使用了所有的气象数据,因此KGE (0.722)、NSE (0.796)和R2 (0.964)均较高,而误差(RMSE和PBIAS分别为0.641 mm/d和-50.264%)较低,因此Valiantzas-M1可靠性较高。
| Valiantzas模型 Valiantzas models |
输入气象因子 Input meteorological factors |
缺失气象因子 Missing meteorological factors |
KGE | NSE | R2 | RMSE (mm/d) | PBIAS (%) |
| Valiantzas-M1 | Tmax,Tmin,n,RH,u2 | — | 0.722 | 0.796 | 0.964 | 0.641 | -50.264 |
| Valiantzas-M2 | Tmax,Tmin,n,RH | u2 | 0.667 | 0.691 | 0.980 | 0.820 | -70.675 |
| Valiantzas-M2-modify | Tmax,Tmin,n,RH | u2 | 0.725 | 0.811 | 0.980 | 0.616 | -49.939 |
| Valiantzas-M3 | Tmax,Tmin,RH | n,u2 | 0.702 | 0.411 | 0.827 | 0.988 | -82.747 |
| Valiantzas-M4 | Tmax,Tmin,n,RH | u2 | 0.661 | 0.703 | 0.980 | 0.916 | -68.980 |
| Valiantzas-M5 | Tmax,Tmin,n | RH,u2 | 0.672 | 0.753 | 0.953 | 0.753 | -56.245 |
Valiantzas-M2、Valiantzas-M2-modify和Valiantzas-M4模型均为风速缺失情况下的ET0计算模型。基于广西气象站点风速修正后的Valiantzas-M2-modify模型能更好地模拟ET0,相比于Valiantzas-M2模型,其KGE和NSE分别提高了8.7%和17.4%,RMSE和PBIAS分别降低了24.9%和29.3%。Valiantzas-M4模型的模拟精度与Valiantzas-M2相当。综合来看,缺失风速时,Valiantzas-M2-modify模型在非喀斯特地区较为适用。
同时缺失太阳辐射和风速、仅使用气温和相对湿度的Valiantzas-M3模拟精度较低,NSE最低(仅为0.411)且误差较大(RMSE为0.988 mm/d,PBIAS为-82.747%)。
Valiantzas-M5模型仅使用气温和日照时数(相对湿度和风速缺失),具有足够的精度,NSE和R2分别达到0.753和0.953。
由图 2可见,FAO-56 P-M模型与Valiantzas系列模型计算的ET0值在年内的变化趋势较一致,均呈“几”字形分布。各个模型计算的ET0值均在7月最大,分别为116.3 mm、142.2 mm、149.2 mm、142.2 mm、143.3 mm、150.0 mm和146.9 mm;在1月最小,分别为44.1 mm、48.5 mm、52.7 mm、47.8 mm、56.5 mm、52.0 mm和48.1 mm。Valiantzas系列模型均高估了各个月的ET0值,Valiantzas-M1、Valiantzas-M2、Valiantzas-M2-modify、Valiantzas- M3、Valiantzas-M4和Valiantzas-M5分别高估了19.5%、27.6%、19.5%、31.8%、26.9%和22.1%,可见Valiantzas-M1和Valiantzas-M2-modify模型模拟的ET0值与FAO-56 P-M模型最接近。
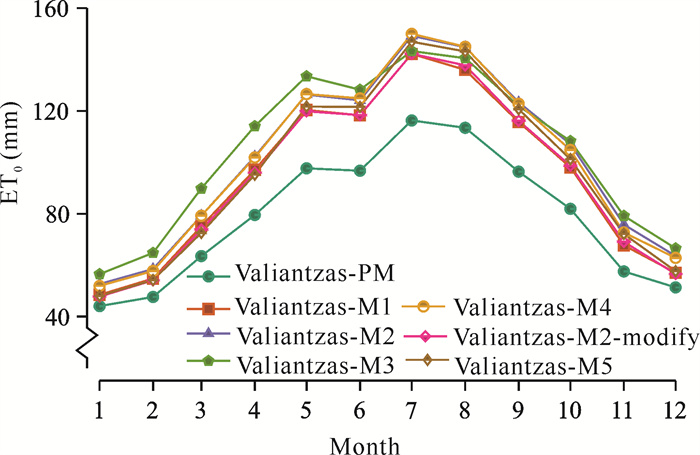
|
| 图 2 2010/1-2015/6非喀斯特地区FAO-56 P-M模型与Valiantzas模型模拟ET0的各月均值 Fig. 2 Monthly average value of ET0 stimulated by FAO-56 P-M model and Valiantzas models in non-karst area during Jan, 2010 to Jun, 2015 |
2.3 Valiantzas模型与其他经验模型模拟精度比较
4个经验模型在喀斯特站点的精度如表 5所示。其中Turk模型与Valiantzas-M2、Valiantzas-M2-modify及Valiantzas-M4模型具有相同的输入变量(Tmax,Tmin,n,RH),其KGE和NSE均高于这3个Valiantzas简化模型,且RMSE和PBIAS的绝对值均低于这3个Valiantzas简化模型,说明在喀斯特地区缺失风速的情况下,Turk模型模拟ET0的可靠性高于相同输入下的Valiantzas简化模型。Makkink模型、Priestley-Taylor模型、Irmark-Allen与Valiantzas-M5模型具有相同的输入变量(Tmax,Tmin,n),可见Makkink精度最高,其次为Valiantzas-M5模型、Priestley-Taylor模型和Irmark-Allen模型,表明只有温度和日照时数时,Makkink模型适用于喀斯特地区的ET0估算。
| 经验模型 Empirical models |
输入气象因子 Input meteorological factors |
缺失气象因子 Missing meteorological factors |
KGE | NSE | R2 | RMSE (mm/d) | PBIAS (%) |
| Turk | Tmax,Tmin,n,RH | u2 | 0.746 | 0.852 | 0.941 | 0.537 | -31.606 |
| Makkink | Tmax,Tmin,n | RH,u2 | 0.841 | 0.905 | 0.948 | 0.380 | 22.941 |
| Priestley-Taylor | Tmax,Tmin,n | RH,u2 | 0.615 | 0.694 | 0.925 | 0.890 | -61.976 |
| Irmark-Allen | Tmax,Tmin,n | RH,u2 | 0.712 | 0.315 | 0.927 | 0.979 | -92.402 |
4个经验模型在非喀斯特站点的精度如表 6所示。其中Turk模型与Valiantzas-M2模型、Valiantzas-M2-modify模型、Valiantzas-M4模型具有相同的输入变量(Tmax,Tmin,n,RH),根据NSE、RMSE,Valiantzas-M2-modify模型精度最高,其次为Turk模型,说明在缺失风速的情况下,Valiantzas-M2-modify模型更适用于非喀斯特地区的ET0模拟。同理可见,Makkink模型、Priestley-Taylor模型、Irmark-Allen模型与Valiantzas-M5模型具有相同的输入变量(Tmax,Tmin,n),Makkink模型精度最高(具有最高的KGE、NSE和绝对值最低的RMSE、PBIAS),其次为Valiantzas-M5模型、Priestley-Taylor模型和Irmark-Allen,表明只有温度和日照时数时,Makkink模型是非喀斯特地区ET0的最佳估算模型。
| 经验模型 Empirical models |
输入气象因子 Input meteorological factors |
缺失气象因子 Missing meteorological factors |
KGE | NSE | R2 | RMSE (mm/d) | PBIAS (%) |
| Turk | Tmax,Tmin,n,RH | u2 | 0.726 | 0.808 | 0.944 | 0.626 | -44.101 |
| Makkink | Tmax,Tmin,n | RH,u2 | 0.848 | 0.922 | 0.947 | 0.356 | 14.696 |
| Priestley-Taylor | Tmax,Tmin,n | RH,u2 | 0.579 | 0.623 | 0.933 | 1.039 | -77.679 |
| Irmark-Allen | Tmax,Tmin,n | RH,u2 | 0.696 | 0.255 | 0.934 | 1.066 | -101.348 |
3 讨论
桂西北以喀斯特峰丛洼地为基本景观单元,该地貌水源涵养能力低、易旱、易涝,且“十里不同天”,气象因子(降水量、温度、湿度和光照等)时空变异大,这使得ET0经验模型的使用受到限制。Valiantzas等[11, 12]根据气象因子之间存在一定的统计关系这一事实,对FAO-56 P-M模型进行了具有物理意义的简化,因此与其他经验模型相比具有较强的普适性。例如,从表 3-表 6可见,Valiantzas系列模型在喀斯特与非喀斯特地区表现较为稳定,而Turk模型在喀斯特地区的表现优于非喀斯特地区。这可能是由于Turk模型具有调节因子WRH(RH≤50%时,WRH取1;RH>50%时,WRH取0),而RH在广西喀斯特地区(桂西北)通常小于非喀斯特地区(桂东南)[1],这使得该模型在喀斯特地区引入相对湿度的概率更大,从而在该地区具有更高的精度。
Wang等[3]统计了2010-2014年广西24个气象站点的多年平均气象数据,结果显示大多数站点(都安、凤山、北海和涠洲岛)的平均风速均小于世界平均风速(2.00 m/s)。本研究使用广西喀斯特和非喀斯特10个站点的平均风速来代替风速缺失值,而非使用世界平均风速,发现能够提高ET0的预测精度。Djaman等[18]也发现,在缺失风速数据的Sahelian地区,使用2.00 m/s的世界平均风速作为代替值时,Valiantzas模型高估了该地区的ET0 4%-35%,其RMSE为0.59-2.11 mm/d,误差较大;使用该地区平均风速校正后,ET0模拟精度显著提高,特别是对于较低的ET0值(ET0<6 mm/d)。下一步拟使用喀斯特和非喀斯特地区更多气象站点和更长时间序列的风速值来进一步降低预测误差。
基于5个模型评价指标,如喀斯特地区Valiantzas-M1模型、Valiantzas-M2模型和Valiantzas-M2-modify模型,R2分别为0.969,0.977和0.978,而RMSE值分别为0.557 mm/d、0.776 mm/d和0.563 mm/d,PBIAS分别为-40.785%、-65.119%和-43.460%;且Valiantzas-M2-modify模型和Valiantzas-M4模型的R2值(均为0.978)相同,但RMSE(分别为0.563 mm/d和0.765 mm/d)和PBIAS(分别为-43.460%和-62.921%)相差较大,可见R2对ET0模拟敏感性较差,不适合单独用于ET0预测模型的评价,须结合NSE、KGE、RMSE和PBIAS等指标综合评价。与喀斯特地区类似,在非喀斯特地区,Valiantzas-M2模型、Valiantzas-M2-modify模型和Valiantzas-M4模型的R2值均相同(0.980),而NSE(0.691,0.811和0.703)、KGE(0.667,0.725和0.661)、RMSE(0.820 mm/d、0.616 mm/d和0.916 mm/d)和PBIAS(-70.675%、-49.939%和-68.980%)则相差较大,同样说明R2值不适合单独用于ET0预测模型的评价,这主要是由于R2值忽略了模型在低值区的表现[19]。因此,在评价ET0预测模型时,除了R2,还应结合其他评价指标,如NSE、KGE等。
从PBIAS值以及图 1、图 2可见,所有的Valiantzas模型(包括Valiantzas-M2的修正模型)均高估了ET0值。Valiantzas系列模型是基于全球2 000个气象站点数据,并通过数值模拟方法简化FAO-56 P-M模型得到的[11, 12],因此其ET0计算值与FAO-56 P-M模型的计算结果相比具有一定的误差,表现为高估了ET0值。而在Senegal河流域的研究发现,Valiantzas系列模型低估了ET0值[20],这可能是由于在不同气候区,ET0的敏感性气象要素不同。
4 结论使用完备气象要素的Valiantzas-M1模型在喀斯特和非喀斯特地区均表现最好,且其形式简单,便于进行ET0对气象因子的敏感性分析,可代替FAO-56 P-M模型。缺失风速时,在喀斯特地区,Turk模型较适用(RMSE为0.537 mm/d);在非喀斯特地区,Valiantzas-M2-modify模型较适用(RMSE为0.616 mm/d)。同时缺失太阳辐射和风速时,Valiantzas-M3可用于ET0估算,在喀斯特和非喀斯特地区其RMSE分别为0.991 mm/d和0.988 mm/d。同时缺失相对湿度和风速时,Makkink模型最佳。此外,由于Valiantzas系列模型是基于全球气象站点数据简化FAO-56 P-M模型而来的,因此高估了广西地区的ET0值,在应用时需进行校正。
| [1] |
WANG S, LIAN J J, PENG Y Z, et al. Generalized reference evapotranspiration models with limited climatic data based on random forest and gene expression programming in Guangxi, China[J]. Agricultural Water Management, 2019, 221: 220-230. DOI:10.1016/j.agwat.2019.03.027 |
| [2] |
TABARI H, GRISMER M E, TRAJKOVIC S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions[J]. Irrigation Science, 2013, 31(2): 107-117. DOI:10.1007/s00271-011-0295-z |
| [3] |
WANG S, FU Z Y, CHEN H S, et al. Mechanisms of surface and subsurface runoff generation in subtropical soil-epikarst systems: Implications of rainfall simulation experiments on karst slope[J]. Journal of Hydrology, 2019, 580: 124370. DOI:10.1016/j.jhydrol.2019.124370 |
| [4] |
GAO X L, PENG S Z, XU J Z, et al. Proper methods and its calibration for estimating reference evapotranspiration using limited climatic data in Southwestern China[J]. Archives of Agronomy & Soil Science, 2015, 61(3): 415-426. |
| [5] |
冯禹, 崔宁博, 龚道枝, 等. 基于极限学习机的参考作物蒸散量预测模型[J]. 农业工程学报, 2015, 31(S1): 153-160. |
| [6] |
TRAORE S, GUVEN A. New algebraic formulations of evapotranspiration extracted from gene-expression programming in the tropical seasonally dry regions of West Africa[J]. Irrigation Science, 2013, 31(1): 1-10. DOI:10.1007/s00271-011-0288-y |
| [7] |
DJAMAN K, BALDE A B, SOW A. Evaluation of sixteen reference evapotranspiration methods under sahelian conditions in the Senegal River Valley[J]. Journal of Hydrology: Regional Studies, 2015, 3: 139-159. DOI:10.1016/j.ejrh.2015.02.002 |
| [8] |
王升, 付智勇, 陈洪松, 等. 基于随机森林算法的参考作物蒸发蒸腾量模拟计算[J]. 农业机械学报, 2017, 48(3): 302-309. |
| [9] |
YASSIN M A, ALAZBA A A, MATTAR M A. Artificial neural networks versus gene expression programming for estimating reference evapotranspiration in arid climate[J]. Agricultural Water Management, 2016, 163: 110-124. DOI:10.1016/j.agwat.2015.09.009 |
| [10] |
YIN Y H, WU S H, CHEN G, et al. Attribution analyses of potential evapotranspiration changes in China since the 1960s[J]. Theoretical & Applied Climatology, 2010, 101(1/2): 19-28. |
| [11] |
VALIANTZAS J D. Simplified forms for the standardized FAO-56 Penman-Monteith reference evapotranspiration using limited weather data[J]. Journal of Hydrology, 2013, 505: 13-23. DOI:10.1016/j.jhydrol.2013.09.005 |
| [12] |
VALIANTZAS J D. Simplified limited data Penman's ET0 formulas adapted for humid locations[J]. Journal of Hydrology, 2015, 524: 701-707. DOI:10.1016/j.jhydrol.2015.03.021 |
| [13] |
DJAMAN K, RUDNICK D, MEL V, et al. Evaluation of Valiantzas' simplified forms of the FAO-56 Penman-Monteith reference evapotranspiration model in a humid climate[J]. Journal of Irrigation & Drainage Engineering, 2017, 143(8): 06017005. DOI:10.1061/(ASCE)IR.1943-4774.0001191 |
| [14] |
VALIPOUR M. Investigation of Valiantzas' evapo-transpiration equation in Iran[J]. Theoretical and Applied Climatology, 2015, 121(1/2): 267-278. |
| [15] |
吴丽萍, 陈洪松, 连晋姣, 等. 喀斯特与非喀斯特地区参考作物蒸散量时空变化分析——以广西壮族自治区为例[J]. 中国生态农业学报, 2017, 25(10): 1508-1517. |
| [16] |
VALIANTZAS J D. Simple ET0 forms of Penman's equation without wind and/or humidity data.Ⅱ: Comparisons with reduced Set-FAO and other methodologies[J]. Journal of Irrigation & Drainage Engineering, 2013, 139(1): 9-19. |
| [17] |
张荣, 庞博, 徐宗学, 等. 基于多准则的城市雨洪模型不确定性分析方法[J]. 水力发电学报, 2018, 37(6): 62-73. |
| [18] |
DJAMAN K, IRMAK S, KABENGE I, et al. Evaluation of FAO-56 penman-monteith model with limited data and the valiantzas models for estimating grass-reference evapotranspiration in Sahelian conditions[J]. Journal of Irrigation and Drainage Engineering, 2016, 142(11): 04016044. DOI:10.1061/(ASCE)IR.1943-4774.0001070 |
| [19] |
ASCHONITIS V G, LEKAKIS E, TZIACHRIS P, et al. A ranking system for comparing models' performance combining multiple statistical criteria and scenarios: The case of reference evapotranspiration models[J]. Environmental Modelling and Software, 2019, 114(APR.): 98-111. |
| [20] |
NDIAYE P M, BODIAN A, DIOP L, et al. Evaluation and calibration of alternative methods for estimating reference evapotranspiration in the Senegal River Basin[J]. Hydrology, 2020, 7(2): 24. DOI:10.3390/hydrology7020024 |



