2. 广西混杂计算与集成电路设计分析重点实验室,广西南宁 530006;
3. 广西高校复杂系统与智能计算重点实验室,广西南宁 530006
2. Guangxi Key Laboratory of Hybrid Computation & IC Design Analysis, Nanning, Guangxi, 530006, China;
3. Key Laboratory of Guangxi High Schools Complex System & Computational Intelligence, Nanning, Guangxi, 530006, China
群智能优化算法是人们通过对自然界中某些生物体的功能、特点和作用机理的观察和理解,或者对自然界中某些自然或物理现象的分析和研究,从中挖掘出其中蕴含的运行规律或机制,并基于对其运行规律或机制的模拟而构建的随机搜索算法。迄今,国内外学者先后提出了诸如遗传算法(GA)[1]、粒子群算法(PSO)[2]、蚁群算法(ACO)[3, 4]、人工蜂群算法(ABC)[5]、蝗虫优化算法(Grasshopper Optimization Algorithm, GOA)[6]、正弦余弦算法(SCA)[7]、鲸鱼算法(WOA)[8]、蝴蝶优化算法(BOA)[9]等群智能优化算法。这些群智能优化算法的提出为解决工程等的优化问题提供了新的技术支持。
GOA是Saremi等[6]基于对蝗虫觅食行为的模拟而提出的一种新的群智能随机优化算法。GOA分为勘探和开发两个步骤,局部搜索能力较强,但全局搜索能力偏弱,故该算法规避陷入局部最优的能力不强。针对GOA的不足,Yildiz等[10]提出一种改进GOA,通过与精英对立学习机制杂交来提高算法的全局搜索能力,并利用工程中的具体优化实例来验证该算法的优化性能。Reddy等[11]利用遗传算子来改善勘探和开发之间的平衡,利用差分进化策略来指导算法搜索,以提高算法搜索效率。与标准GOA相比较,其改进的GOA在一定程度上提升了优化精度和收敛速度,然而提升的程度比较有限,仍有待进一步提高。尹德鑫等[12]利用Fuch初始化种群,通过引入正余弦因子和非线性惯性权重来提高算法的全局搜索能力,但在一定程度上增加了算法的时间复杂度。刘奇等[13]利用反向学习机制与混沌映射来加快算法的收敛速度,以增强算法的搜索能力,并利用红细胞供应预测实例来验证其改进算法的有效性。李洋州等[14]利用曲线自适应和模拟退火算法来提高算法的优化性能,其改进GOA的优化性能相较于标准GOA有一定的提高,但在收敛精度和优化精度方面仍有待进一步提升。何庆等[15]采用分段位置更新方式和利用柯西变异算子与反向学习策略对当前最优位置进行变异更新,提高算法跳出局部最优能力,将均匀分布函数引入非线性控制参数,平衡算法全局探索与局部开发,但对当前最优位置进行变异更新会增加算法的迭代次数,从而增加算法的时间复杂度。Luo等[16]通过引入高斯变异、列维飞行策略和反向学习策略来提高算法的收敛速度,但这样处理会增加算法的时间复杂度。林杰等[17]根据概率转换采用不同的位置更新方式,利用正弦余弦来平衡全局探索和局部开发,通过变异选择对最优解进行变异,提高算法的优化精度。然而采用变异选择对最优解进行变异会增加算法的迭代次数,从而增加算法的时间复杂度。杨文珍等[18]利用非线性曲线函数去平衡算法的局部开发和全局探索,引入扰动因子并利用高斯分布增加种群多样性,提高算法的收敛速度,但采用扰动因子和高斯分布增加种群多样性策略会增加算法的时间复杂度。上述文献[10-18]提出的各种版本的改进GOA相较于标准GOA,虽然在优化精度方面有一定的改善,但是仍存在早熟收敛问题,跳出局部极值的能力仍有待提高。本研究针对这些问题,提出一种基于4-乙烯基苯甲醚(4-vinylanisole, 4VA)信息素的蝗虫优化算法(Grasshopper Optimization Algorithm Based on 4-vinylanisole Pheromone, VAGOA)。根据蝗虫生活习性和行为特征的最新研究发现[19, 20],结合标准GOA模型,基于4VA是蝗虫聚集信息素,设计4VA信息素表达式,对于不同蝗虫群体(群居型蝗虫和散居型蝗虫)分别采用不同的搜索策略,以平衡全局探索和局部开发,使算法的全局探索能力和局部开发能力均得到提升,并通过数值实例仿真验证本研究算法的优化性能。
1 蝗虫优化算法蝗虫优化算法(GOA)[6]的基本思想:将蝗虫的生命周期分为幼虫和成虫两个阶段。在幼虫阶段,蝗虫具有跳跃步幅小、移动缓慢、小范围觅食活动的特征,倾向于局部搜索;在成虫阶段,蝗虫具有跳跃步幅大、移动快速、大范围觅食活动的特征,倾向于全局搜索。
GOA模型及步骤如下。
Input:蝗虫种群规模N,搜索空间维数dim,最大迭代次数Tmax,参数cmax和cmin。
① 初始化种群Xi,i=1,…,N。
② 评估每一个体的适应度值, 将最优位置存于
③ 依公式(1)更新参数c:
| $ c=c_{\max }-t\left(c_{\max }-c_{\min }\right) / T_{\max }, $ | (1) |
其中,cmax和cmin分别表示参数c的最大值和最小值,t为当前迭代次数。
④ 蝗虫个体依公式(4)更新位置:
| $ S_i=\sum\limits_{j=1, j \neq i}^N s\left(d_{i j}\right) \hat{d}_{i j}, $ | (2) |
| $ s(r)=f e^{\frac{-r}{l}}-e^{-r}, $ | (3) |
| $ \begin{aligned} X_i^d & =c\left[\sum\limits_{j=1, j \neq i}^N c \frac{u b_d-l b_d}{2} s\left(\left|x_j^d-x_i^d\right|\right)\right. \\ \left.\frac{x_j-x_i}{d_{i j}}\right] & +\hat{T}_d, \end{aligned} $ | (4) |
其中:s(r)表示种群社交影响强度,f为吸引力强度,l为吸引力范围(GOA在仿真实验中取f=0.5,l=1.5);ubd和lbd分别表示第d维度的上下界,dij=
|xjd-xid|为第i个个体与第j个个体在第d维的距离,Si表示种群间的社交作用,xid为第i个个体在第d维的位置。
⑤ 评估每一个体的适应度值,择优更新
⑥ 判断是否满足终止条件,如果是,则转步骤⑦;否则, 重复步骤③-⑤。
⑦ 算法停止,并输出最优位置
根据Guo等[19]和Chen等[20]的最新研究,蝗虫除具有前面已提及的特征外,还具有以下活动习性和生物行为特征:①4VA是蝗虫的聚集信息素。②3′-磷酸腺苷-5′-磷酰硫酸(PAPS)生物合成过程能有效诱导蝗虫的行为转变。抑制PAPS的合成可以促使蝗虫行为从群居状态转变为独居状态。③根据活动行为状态,蝗虫分为群居型蝗虫和散居型蝗虫两种。④群居型蝗虫行为的亢奋是源于4VA信息素的分泌,4VA信息素专门由群居蝗虫释放,4-5只孤立蝗虫的聚集就会触发4VA信息素的产生,而且4VA信息素对蝗虫的吸引力极强。⑤释放4VA信息素的浓度与群居蝗虫发育密度有关,4VA信息素生物合成对于调节迁徙蝗虫的嗅觉吸引力和移动性至关重要。⑥4VA信息素对群居型蝗虫和散居型蝗虫的不同发育阶段都有很强的吸引力,能够响应蝗虫种群密度的变化,随着种群密度增加而增加。⑦根据种群密度显示出两个不同的行为阶段,即独居阶段和蜂拥而至的群居阶段,低密度发育的独居期蝗虫(散居型蝗虫)具有嗜睡和同种排斥的特征,而高密度发育的群居期蝗虫(群居型蝗虫)具有高流动性和同种吸引的特征。⑧散居蝗虫背部是绿色的,蝗虫从散居变成群居一段时间后,背部就会从绿色转换为黑色,行为也会变得亢奋起来。此时的蝗虫胃口很大,所过之处食物全被一扫而空。
本研究基于以上蝗虫活动习性和生物行为特征,设计一种新的采用4VA信息素的蝗虫优化算法。
2.2 构建算法模型 2.2.1 4VA信息素表达式的设计4VA是蝗虫聚集信息素,能够响应蝗虫种群密度的变化,其浓度随着种群密度的增加而增加。因此,某处(蝗虫爱吃的)食物越丰富,该处引来的蝗虫就越多,从而该处蝗虫释放出的4VA信息素浓度也就越高。即哪里的食物越丰富,哪里的4VA信息素浓度就越高。基于此,设群体于t时刻找到最优位置,即食物最丰富、4VA信息素浓度最大位置是xbest(t),i个体于t时刻位于xi(t)。由于i个体嗅觉受体在t时刻闻到4VA信息素的强弱与位置xbest(t)的4VA信息素浓度、距离有关,也与其嗅觉受体感应能力有关,故设计4VA信息素表达式如下:
| $ \mathrm{VA}=\beta_0 \exp \left(-q_i h_i \cdot\left(\frac{t}{T_{\max }}\right)^2\right), $ | (5) |
其中,β0=2,qi=|f(xbest(t))-f(xi(t))|,
f(xbest(t))表示位置xbest(t)的适应度值(即此处4VA信息素浓度),f(xi(t))表示i个体的嗅觉受体感应能力(以适应度值表示);hi=‖xbest(t)-xi(t)‖为xbest(t)与xi(t)的距离,Tmax为最大迭代次数,t为当前迭代次数。
公式(5)说明i个体嗅觉感应到4VA信息素的强弱,不仅跟其与xbest(t)的距离、与其嗅觉受体感应能力和位置xbest(t)的4VA信息素浓度有关,还跟时间有关,4VA信息素随时间的增加而逐渐变弱。
2.2.2 不同蝗虫群体搜索方法的设计① 群居型蝗虫搜索方法设计。由于4VA信息素由群居型蝗虫释放,群居型蝗虫具有同种吸引特征,故群居型蝗虫释放的4VA信息素会诱惑其他蝗虫前来聚集(图 1)。因此,本研究结合GOA的公式(4),将4VA信息素与高斯分布相结合,设计群居型蝗虫搜索方法如下。
首先利用正态分布选取数a:
| $ a \sim N\left(0, \sigma^2\right)。$ | (6) |
在仿真实验中,取σ=t/Tmax。然后按公式(7)更新位置。
| $ \begin{aligned} & x_i^d(t+1)=a\left(\sum\limits_{j=1, j \neq i}^N \operatorname{VA} \cdot \frac{u b_d-l b_d}{2} \cdot\right. \\ &\left.\frac{x_j^d(t)-x_i^d(t)}{d_{i j}}\right)+\hat{T}_d, \end{aligned} $ | (7) |
本研究称公式(7)为聚集搜索方法。xid(t)为xi(t)的第d维,d=1,…,D,D为搜索空间的维数。本研究算法利用a来调整蝗虫个体的位置更新,进一步提升算法的局部开发能力。
设xbest(t)=[xbest, 1(t), …,xbest, D(t)]为群体于t时刻找到的最优位置,此时xbest(t)的4VA信息素浓度最大,故有一部分群居型蝗虫被诱惑到xbest(t)的周围觅食。针对这部分蝗虫,本研究设计其位置更新公式如下:
| $ x_{i, j}(t+1)=\xi_{i, j}, $ | (8) |
其中,ξi, j为[xbest, j(t)-ε, xbest, j(t)+ε]中的随机数,0 < ε≪1,j=1, …, D。在仿真实验中,取ε=1/t2。
② 散居型蝗虫搜索方法设计。尽管处于独居状态的蝗虫的觅食活动具有随意性,但4VA信息素对散居型蝗虫的不同发育阶段都有很强的吸引力。因此,当散居型蝗虫闻到其他蝗虫释放的4VA气味时,就会朝4VA散发地进发。针对散居型蝗虫,本研究设计其位置更新公式如下:
| $ \begin{gathered} x_i^d(t+1)=x_i^d(t)+\mathrm{VA} \cdot\left[r _ { 1 } \cdot \left(x_k^d(t)-\right.\right. \\ \left.\left.x_i^d(t)\right)+r_2 \cdot\left(x_p^d(t)-x_i^d(t)\right)\right], \end{gathered} $ | (9) |
本研究称公式(9)为分散搜索方法。其中r1和r2均为[0, 1]中的随机数,xk(t)和xp(t)为从散居型蝗虫当中随机选取的两只蝗虫,xkd(t)和xpd(t)分别为xk(t)和xp(t)的第d维。
2.3 群居型蝗虫与散居型蝗虫的区分方法由于“群居型蝗虫胃口大,所过之处食物全被一扫而空”,故认为群居型蝗虫的搜索(觅食)能力相对较强;“散居型蝗虫具有嗜睡和同种排斥特征”,故认为散居型蝗虫的搜索(觅食)能力相对较弱。因此,本研究根据蝗虫个体觅食能力强弱来区分其是群居型蝗虫还是散居型蝗虫。
区分方法如下:设至t时刻群体找到的最优位置为xbest(t),相应的适应度值为f(xbest(t))。首先给定阈值ρ>1(本研究在实验中取ρ=1.4)。
Rule 1:若f(xi(t))≤2f(xbest(t)),则认为i蝗虫为群居蝗虫。此时,若ρ·f(xbest(t))<f(xi(t))≤2f(xbest(t)),则其按公式(6)、(7)更新位置;否则按公式(8)更新位置。
Rule 2:若2f(xbest(t))≤f(xi(t)),则认为i蝗虫为散居蝗虫,并按公式(9)更新位置。
2.4 算法实现步骤本研究算法步骤和流程如下。
输入:种群规模N,搜索空间维数D,最大迭代次数Tmax。
步骤1:初始化种群Xi,i=1,…,N。
步骤2:评价每一个体的适应度值,将最优个体位置存储于
步骤3:按群居蝗虫与散居蝗虫的区分方法将种群分为群居蝗虫与散居蝗虫两个子群。
步骤4:群居蝗虫按“Rule 1”选择公式(6)、(7)或公式(8)更新位置;散居蝗虫按公式(9)更新位置。
步骤5:评价每一个体的适应度值,择优更新
步骤6:判断是否满足停止条件,若满足,则转Step 7;否则重复Step 3-Step 5。
步骤7:算法停止,输出最优位置
为了测试本研究算法(VAGOA)的优化性能,将VAGOA与标准GOA[6]、PSO[2],以及从各种改进版本GOA当中选择的比较有代表性的SA_CAGOA[14]和HCUGOA[15]进行算法数值实验对比分析。选取12个典型的基准测试函数(表 1)作为本次算法性能测试分析(均为求最小值问题)。
| 函数 Function |
类型 Type |
维数 Dimension |
搜索区间 Search interval |
最优值 Optimal value |
| Unimodal | 30/100/200 | [-100, 100] | 0 | |
| Unimodal | 30/100/200 | [-100, 100] | 0 | |
| Multimodal | 30/100/200 | [-100, 100] | 0 | |
| Multimodal | 30/100/200 | [-100, 100] | 0 | |
| Multimodal | 30/100/200 | [-5.12, 5.12] | 0 | |
| Multimodal | 30/100/200 | [-10, 10] | 0 | |
| Unimodal | 30/100/200 | [-100, 100] | 0 | |
| Unimodal | 30/100/200 | [-10, 10] | 0 | |
| Multimodal | 30/100/200 | [0.25, 10] | -1 | |
| Multimodal | 30/100/200 | [-100, 100] | 0 | |
| Unimodal | 2 | [-10, 10] | 0 | |
| F12(x)=0.26(x12+x22)-0.48x1x2 | Unimodal | 2 | [-10, 10] | 0 |
3.2 结果与分析
为保证实验结果的对照与比较的客观和公平,5种算法统一设置群体规模为30,最大迭代次数为200。对于GOA、HCUGOA、SA_CAGOA 3种算法,其参数设置与相应的文献保持一致,即cmax=0.1,cmin=0.000 04。对于SA_CAGOA,设置初始温度T0=100,结束温度T=1,退火系数r=0.95。
为了验证本研究算法(VAGOA)的性能,对表 1中的12个基准测试函数进行求解。表 1中既有单峰函数,也有多峰函数。单峰函数主要用来测试算法的收敛速度,多峰函数主要用来测试算法的全局搜索能力(探索和开发能力)和规避陷入局部最优的能力。本研究以最优值、最差值、平均值和标准差作为算法性能评价指标,这些评价指标总体上反映了算法优化能力的强弱和算法稳定性的优劣。为了避免随机性对实验结果的影响,本研究在数值实验中将5种算法对每个测试函数均独立进行30次实验,并记录最优值、最差值、平均值、标准差等实验数据。高维测试函数(F1-F10)实验结果比较数据见表 2,低维测试函数(F11-F12)实验结果比较数据见表 3。
| 函数 Function |
算法 Algorithm |
D=30 | D=100 | D=200 | |||||||||||
| 最优值 Optimal value |
最差值 Worst value |
平均值 Mean value |
标准差 Std. |
最优值 Optimal value |
最差值 Worst value |
平均值 Mean value |
标准差 Std. |
最优值 Optimal value |
最差值 Worst value |
平均值 Mean value |
标准差 Std. |
||||
| F1 | VAGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| GOA | 1.23E+05 | 1.70E+05 | 1.54E+05 | 1.12E+04 | 1.23E+05 | 1.70E+05 | 1.54E+05 | 1.12E+04 | 1.60E+24 | 3.14E+44 | 1.28E+43 | 5.80E+43 | |||
| PSO | 4.80E+04 | 1.73E+05 | 1.03E+05 | 3.64E+04 | 4.80E+04 | 1.73E+05 | 1.03E+05 | 3.64E+04 | 1.63E+02 | 3.95E+33 | 1.35E+32 | 7.21E+32 | |||
| HCUGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |||
| SA_CAGOA | 2.38E-12 | 1.04E-09 | 1.88E-10 | 2.54E-10 | 2.38E-12 | 1.04E-09 | 1.88E-10 | 2.54E-10 | 4.27E-08 | 1.16E-03 | 3.47E-04 | 3.49E-04 | |||
| F2 | VAGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| GOA | 1.50E+02 | 1.10E+03 | 4.68E+02 | 2.15E+02 | 3.29E+01 | 4.34E+01 | 3.92E+01 | 2.21E+00 | 6.00E+04 | 7.51E+04 | 6.96E+04 | 3.43E+03 | |||
| PSO | 4.45E+01 | 1.77E+03 | 6.54E+02 | 7.17E+02 | 1.30E+01 | 4.20E+01 | 2.32E+01 | 7.34E+00 | 2.85E+04 | 4.41E+04 | 3.69E+04 | 4.39E+03 | |||
| HCUGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |||
| SA_CAGOA | 6.98E-15 | 1.65E-07 | 5.50E-09 | 3.01E-08 | 5.11E-15 | 8.45E-11 | 8.78E-12 | 1.82E-11 | 1.82E-13 | 6.02E-10 | 1.31E-10 | 1.82E-10 | |||
| F3 | VAGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| GOA | 1.25E+00 | 2.68E+00 | 1.89E+00 | 3.27E-01 | 3.44E+01 | 4.32E+01 | 3.94E+01 | 2.19E+00 | 1.05E+02 | 1.20E+02 | 1.13E+02 | 4.35E+00 | |||
| PSO | 1.04E+00 | 4.14E+00 | 1.65E+00 | 8.86E-01 | 1.31E+01 | 3.99E+01 | 2.37E+01 | 7.51E+00 | 3.95E+01 | 7.33E+01 | 5.87E+01 | 7.88E+00 | |||
| HCUGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |||
| SA_CAGOA | 2.11E-15 | 1.40E-07 | 7.64E-09 | 2.98E-08 | 2.22E-16 | 1.17E-10 | 1.09E-11 | 2.20E-11 | 7.77E-16 | 7.37E-11 | 6.89E-12 | 1.48E-11 | |||
| F4 | VAGOA | 0.000E+00 | 0.000E+00 | 0.000E+00 | 0.000E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| GOA | 1.892E+04 | 9.956E+04 | 4.520E+04 | 1.813E+04 | 5.69E+06 | 8.26E+06 | 7.29E+06 | 5.85E+05 | 3.95E+07 | 4.73E+07 | 4.35E+07 | 1.98E+06 | |||
| PSO | 1.075E+04 | 2.352E+05 | 9.899E+04 | 5.824E+04 | 1.29E+06 | 7.93E+06 | 3.90E+06 | 1.62E+06 | 1.28E+07 | 4.73E+07 | 2.38E+07 | 7.21E+06 | |||
| HCUGOA | 0.000E+00 | 0.000E+00 | 0.000E+00 | 0.000E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |||
| SA_CAGOA | 5.163E-13 | 2.128E-05 | 1.276E-06 | 4.874E-06 | 8.91E-12 | 3.95E-05 | 1.33E-06 | 7.20E-06 | 3.91E-14 | 5.48E-07 | 5.82E-08 | 1.19E-07 | |||
| F5 | VAGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| GOA | 1.52E+02 | 2.76E+02 | 2.18E+02 | 3.11E+01 | 1.05E+03 | 1.29E+03 | 1.17E+03 | 5.22E+01 | 2.79E+03 | 3.08E+03 | 2.96E+03 | 6.66E+01 | |||
| PSO | 1.66E+02 | 3.05E+02 | 2.47E+02 | 3.96E+01 | 8.46E+02 | 1.52E+03 | 1.24E+03 | 1.59E+02 | 2.01E+03 | 3.20E+03 | 2.59E+03 | 3.45E+02 | |||
| HCUGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |||
| SA_CAGOA | 0.00E+00 | 3.30E-07 | 3.16E-08 | 8.57E-08 | 1.14E-13 | 4.54E-09 | 3.97E-10 | 8.76E-10 | 2.27E-13 | 1.99E-07 | 6.93E-09 | 3.62E-08 | |||
| F6 | VAGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| GOA | 6.39E+00 | 2.31E+01 | 1.42E+01 | 3.84E+00 | 1.33E+02 | 2.09E+02 | 1.65E+02 | 1.57E+01 | 4.18E+02 | 4.76E+02 | 4.50E+02 | 1.44E+01 | |||
| PSO | 2.80E+00 | 3.87E+01 | 1.97E+01 | 8.86E+00 | 9.80E+01 | 2.08E+02 | 1.55E+02 | 2.64E+01 | 2.66E+02 | 4.75E+02 | 3.95E+02 | 4.48E+01 | |||
| HCUGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |||
| SA_CAGOA | 7.93E-09 | 4.09E-05 | 3.29E-06 | 9.29E-06 | 1.21E-08 | 1.17E-04 | 1.84E-05 | 3.55E-05 | 2.49E-08 | 2.18E-04 | 4.19E-05 | 5.96E-05 | |||
| F7 | VAGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| GOA | 3.06E+03 | 2.05E+04 | 9.85E+03 | 4.86E+03 | 1.05E+03 | 1.29E+03 | 1.17E+03 | 5.22E+01 | 1.66E+06 | 6.84E+06 | 3.40E+06 | 1.34E+06 | |||
| PSO | 1.94E+04 | 6.69E+04 | 4.71E+04 | 1.15E+04 | 8.46E+02 | 1.52E+03 | 1.24E+03 | 1.59E+02 | 6.00E+05 | 2.74E+06 | 1.60E+06 | 3.66E+05 | |||
| HCUGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |||
| SA_CAGOA | 4.01E-11 | 1.96E-04 | 3.56E-05 | 5.08E-05 | 1.14E-13 | 4.54E-09 | 3.97E-10 | 8.76E-10 | 3.32E-10 | 2.54E-02 | 2.13E-03 | 4.97E-03 | |||
| F8 | VAGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| GOA | 8.42E+01 | 3.80E+06 | 2.24E+05 | 7.59E+05 | 1.60E+24 | 3.14E+44 | 1.28E+43 | 5.80E+43 | 1.60E+24 | 3.14E+44 | 1.28E+43 | 5.80E+43 | |||
| PSO | 1.34E+01 | 1.28E+02 | 7.44E+01 | 2.90E+01 | 1.63E+02 | 3.95E+33 | 1.35E+32 | 7.21E+32 | 1.63E+02 | 3.95E+33 | 1.35E+32 | 7.21E+32 | |||
| HCUGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |||
| SA_CAGOA | 4.23E-08 | 6.82E-04 | 7.84E-05 | 1.52E-04 | 4.27E-08 | 1.16E-03 | 3.47E-04 | 3.49E-04 | 4.27E-08 | 1.16E-03 | 3.47E-04 | 3.49E-04 | |||
| F9 | VAGOA | -1.00E+00 | -1.00E+00 | -1.00E+00 | -1.00E+00 | -1.00E+00 | -1.00E+00 | -1.00E+00 | -1.00E+00 | -1.00E+00 | -1.00E+00 | -1.00E+00 | -1.00E+00 | ||
| GOA | -9.40E-01 | -4.03E-01 | -6.50E-01 | 1.30E-01 | -4.57E-01 | -1.57E-01 | -2.45E-01 | 6.37E-02 | -2.40E-01 | -6.03E-02 | -1.39E-01 | 3.52E-02 | |||
| PSO | -9.27E-01 | -8.35E-01 | -8.94E-01 | 2.45E-02 | -5.05E-01 | -1.46E-01 | -3.49E-01 | 7.26E-02 | -4.55E-01 | -8.74E-02 | -2.69E-01 | 7.91E-02 | |||
| HCUGOA | -3.71E-01 | -1.21E-01 | -2.23E-01 | 6.11E-02 | -2.20E-01 | -2.61E-02 | -1.02E-01 | 4.70E-02 | -1.03E-01 | -1.76E-02 | -6.23E-02 | 2.29E-02 | |||
| SA_CAGOA | -3.27E-01 | -1.04E-01 | -2.23E-01 | 6.02E-02 | -1.46E-01 | -4.50E-02 | -1.01E-01 | 2.71E-02 | -1.27E-01 | -1.56E-02 | -5.70E-02 | 2.42E-02 | |||
| F10 | VAGOA | 8.88E-16 | 8.88E-16 | 8.88E-16 | 0.00E+00 | 8.88E-16 | 8.88E-16 | 8.88E-16 | 0.00E+00 | 8.88E-16 | 8.88E-16 | 8.88E-16 | 0.00E+00 | ||
| GOA | 2.00E+01 | 2.03E+01 | 2.01E+01 | 7.33E-02 | 2.08E+01 | 2.10E+01 | 2.09E+01 | 6.56E-02 | 2.11E+01 | 2.13E+01 | 2.12E+01 | 4.59E-02 | |||
| PSO | 2.00E+01 | 2.00E+01 | 2.00E+01 | 3.30E-09 | 2.00E+01 | 2.00E+01 | 2.00E+01 | 0.00E+00 | 2.00E+01 | 2.00E+01 | 2.00E+01 | 0.00E+00 | |||
| HCUGOA | 8.88E-16 | 8.88E-16 | 8.88E-16 | 0.00E+00 | 8.88E-16 | 8.88E-16 | 8.88E-16 | 0.00E+00 | 8.88E-16 | 8.88E-16 | 8.88E-16 | 0.00E+00 | |||
| SA_CAGOA | 2.23E-07 | 1.00E-03 | 2.04E-04 | 3.29E-04 | 1.19E-08 | 5.19E-04 | 6.18E-05 | 1.52E-04 | 2.57E-07 | 1.77E-04 | 9.84E-06 | 3.16E-05 | |||
| Note: Bold type in the table is the test result of the algorithm in this study | |||||||||||||||
| 函数 Function |
算法 Algorithm |
D=2 | |||
| 最优值 Optimal value |
最差值 Worst value |
平均值 Mean value |
标准差 Std. |
||
| F11 | VAGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| GOA | 4.58E-13 | 2.48E-11 | 9.03E-12 | 6.55E-12 | |
| PSO | 9.36E-21 | 9.86E-16 | 4.57E-17 | 1.86E-16 | |
| HCUGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| SA_CAGOA | 1.97E-17 | 5.84E-13 | 1.07E-13 | 1.50E-13 | |
| F12 | VAGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| GOA | 4.65E-14 | 1.01E-11 | 1.61E-12 | 2.07E-12 | |
| PSO | 2.97E-20 | 4.01E-14 | 3.26E-15 | 8.57E-15 | |
| HCUGOA | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | |
| SA_CAGOA | 1.95E-18 | 8.31E-15 | 9.60E-16 | 1.99E-15 |
|
| Note: Bold type in the table is the test result of the algorithm in this study | |||||
针对30,100和200维,本研究算法(VAGOA)找到F1-F9的最优值、最差值、平均值、标准差均与理论最优值相同,HCUGOA找到F1-F8的最优值、最差值、平均值、标准差也与理论最优值相同。VAGOA与HCUGOA找到F10的最优值、最差值、平均值、标准差相同,其他3种算法均没有找到这10个测试函数的理论最优值(表 2)。基于以上分析,不论是求解单峰还是多峰优化问题,相较于其他4种算法,VAGOA全局寻优能力和规避陷入局部最优能力最强、优化精度最高、稳定性更好。
本研究算法(VAGOA)与HCUGOA找到F11和F12的最优值、最差值、平均值、标准差均与理论最优值相等,但VAGOA至41次迭代就已经找到理论最优解,而HCUGOA至175次迭代才找到理论最优解,其他3种算法均没有找到理论最优解(表 3)。基于此,针对低维度优化问题,说明VAGOA相较于4种对比算法具有更快的全局收敛速度,收敛精度更高,稳定性更好。
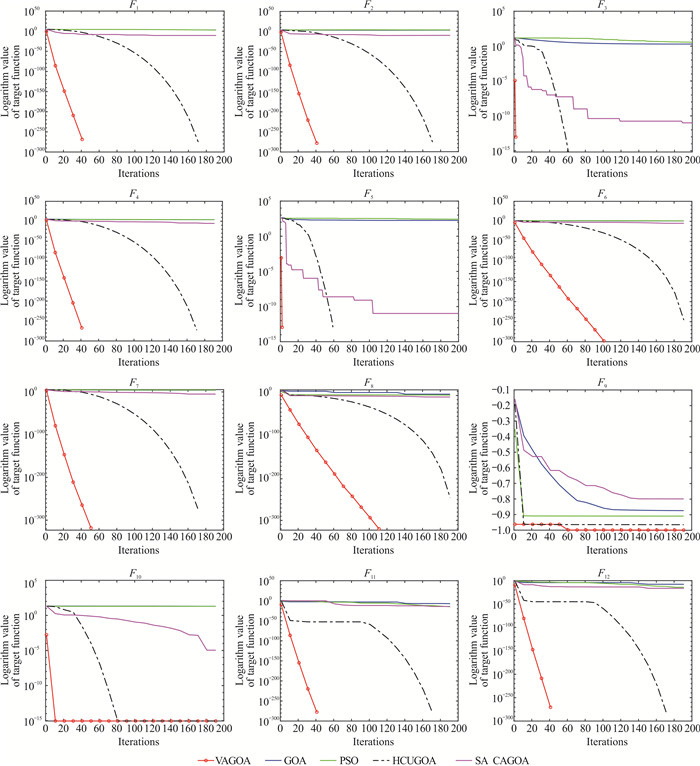
为了更直观地对比本研究算法(VAGOA)、GOA、PSO、HCUGOA和SA_CAGOA 5种算法各自的全局收敛速度和全局搜索能力,给出5种算法求解以上12个基准测试函数的适应度进化曲线对比图(图 2)。相较于GOA、PSO、HCUGOA、SA_CAGOA 4种算法,VAGOA的进化曲线均位于最下方位置,且下降趋势为5种算法中最快,没有出现停滞状态;VAGOA的F1-F9收敛曲线均到达理论最优位置,F10收敛曲线非常接近理论最优位置(图 2)。说明本研究算法(VAGOA)在搜索后期没有陷入局部最优。基于以上分析,相较于GOA、PSO、HCUGOA、SA_CAGOA 4种算法,VAGOA的全局收敛速度明显更快,规避陷入局部最优的能力更强。
|
| 图 2 5种算法进化曲线对比 Fig. 2 Comparison of evolution curves of five algorithms |
4 结论
本研究从以下方面对GOA进行了优化:①根据确定的搜索方法规则,群体中位置较优者采用聚集搜索方法,而位置较劣者则采用分散搜索方法。②从确定的搜索方法规则上看,蝗虫个体可根据自身当前位置的优劣来确定下一步的搜索方法,使其能更快地搜寻到食物源,以增强个体的搜索能力。③对群居型蝗虫和散居型蝗虫分别采用不同的搜索方法,使得算法能基于群体信息反馈,及时分配群居型蝗虫个体数和散居型蝗虫个体数,使群体中从事探索活动的个体数与从事开发活动的个体数得到适当分配,也使种群的多样性得到有效保持,从而提升算法的全局搜索能力。④利用4VA信息素随时间增加而逐渐变弱这一特征,确保群体中时刻都有部分个体开展随机游走(搜索)活动,在保持种群多样性的同时,又增强算法规避陷入局部最优的能力。
本研究针对GOA存在的不足,基于蝗虫活动习性和生物行为特征,提出基于4VA信息素的蝗虫优化算法(VAGOA)。对不同蝗虫群体(群居型蝗虫和散居型蝗虫)分别采用不同的搜索策略,以平衡全局探索和局部开发,使算法全局探索能力和局部开发能力均得到有效提升, 增强了算法的全局寻优能力和规避陷入局部最优的能力。通过求解12个基准测试函数,验证了VAGOA明显比GOA、PSO、HCUGOA、SA_CAGOA 4种算法具有更快的全局收敛速度、更强的规避陷入局部最优的能力、更好的全局搜索能力和稳定性。在后续研究中,将考虑把VAGOA应用于求解TSP优化问题, 进一步验证VAGOA的性能。
| [1] |
HOLLAND J H. Genetic algorithms and the optimal allocation of trials[J]. SIAM Journal on Computing, 1973, 2(2): 88-105. DOI:10.1137/0202009 |
| [2] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Washington, USA: IEEE, 1995, 4: 1942-1948.
|
| [3] |
DORIGO M, MANIEZZO V, COLORNI A. The ant system: Optimization by a colony of cooperating agents[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 1996, 26(1): 29-41. DOI:10.1109/3477.484436 |
| [4] |
SILVA B N, HAN K J. Mutation operator integrated ant colony optimization based domestic appliance scheduling for lucrative demand side management[J]. Future Generation Computer Systems, 2019, 100: 557-568. DOI:10.1016/j.future.2019.05.052 |
| [5] |
KARABOGA D, BASTURK B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459-471. DOI:10.1007/s10898-007-9149-x |
| [6] |
SAREMI S, MIRJALILI S, LEWIS A. Grasshopper optimization algorithm: Theory and application[J]. Advances in Engineering Software, 2017, 105: 30-47. DOI:10.1016/j.advengsoft.2017.01.004 |
| [7] |
GUPTA S, DEEP K. A hybrid self-adaptive sine cosine algorithm with opposition based learning[J]. Expert Systems with Application, 2019, 119: 210-230. DOI:10.1016/j.eswa.2018.10.050 |
| [8] |
MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008 |
| [9] |
ARORA S, SINGH S. Butterfly optimization algorithm: A novel approach for global optimization[J]. Soft Computing, 2019, 23(3): 715-734. DOI:10.1007/s00500-018-3102-4 |
| [10] |
YILDIZ B S, PHOLDEE N, BUREERAT S, et al. Enhanced grasshopper optimization algorithm using elite opposition-based learning for solving real-world engineering problems[J/OL]. Engineering with Computers, 2021[2021-12-13]. https://doi.org/10.1007/s00366-021-01368-w.
|
| [11] |
REDDY K N, BOJJA P. A novel method to solve visual tracking problem: Hybrid algorithm of grasshopper optimization algorithm and differential evolution[J]. Evolutionary Intelligence, 2022, 15: 785-822. DOI:10.1007/s12065-021-00567-0 |
| [12] |
尹德鑫, 张达敏, 蔡朋宸, 等. 基于鸽群算法的Fuch混沌蝗虫算法[J]. 计算机应用研究, 2021, 38(7): 2013-2017. |
| [13] |
刘奇, 陈红梅, 罗川. 基于改进的蝗虫优化算法的红细胞供应预测方法[J]. 计算机科学, 2021, 48(2): 224-230. |
| [14] |
李洋州, 顾磊. 基于曲线自适应和模拟退火的蝗虫优化算法[J]. 计算机应用研究, 2019, 36(12): 3637-3643. |
| [15] |
何庆, 林杰, 徐航. 混合柯西变异和均匀分布的蝗虫优化算法[J]. 控制与决策, 2021, 36(7): 1558-1568. |
| [16] |
LUO J, CHEN H L, ZHANG Q, et al. An improved grasshopper optimization algorithm with application to financial stress prediction[J]. Applied Mathematical Modelling, 2018, 64: 654-668. DOI:10.1016/j.apm.2018.07.044 |
| [17] |
林杰, 何庆. 融合正弦余弦和变异选择的蝗虫优化算法[J]. 小型微型计算机系统, 2021, 42(4): 706-713. DOI:10.3969/j.issn.1000-1220.2021.04.006 |
| [18] |
杨文珍, 何庆, 杜逆索. 具有扰动机制和强化莱维飞行的蝗虫优化算法[J]. 小型微型计算机系统, 2022, 43(2): 247-253. |
| [19] |
GUO X J, YU Q Q, CHEN D F, et al. 4-Vinylanisole is an aggregation pheromone in locusts[J]. Nature, 2020, 584(7822): 584-588. |
| [20] |
CHEN B, TONG X W, ZHANG X, et al. Sulfation modification of dopamine in brain regulates aggregative behavior of animals[J]. National Science Review, 2021, 9(4): nwab163. |




