聚类分析利用数据的内在结构将数据划分为互不相交的子集,是数据分析中的重要课题,长期以来受到机器学习和统计分析领域学者的广泛关注。真实数据中存在一些先验知识,这些先验知识由少量标记数据或专家给出的成对约束表示,但纯粹的无监督聚类算法没有考虑数据中可能存在的先验约束关系或者监督信息,使得学习难度增大。半监督聚类算法[1-4]在大量的无监督数据中仅引入少量的先验信息即可显著提高聚类性能,从而成为近年来的重要研究方向。
半监督聚类算法大体可以分为两类。第一类半监督聚类可同时利用未标记的、足够多的数据和一些先验的知识改进聚类性能。例如,Hong等[5]提出了一种半监督的深度学习框架,可以从小规模的图像中学习更多的判别信息,并将其转移到大规模数据的分类任务中。第二类半监督聚类以强监督的方式使用先验知识,使用标签信息直接指导聚类中心的学习,并以数据驱动的方式对样本进行聚类以学习聚类中心,并得到对聚类有效的表示。例如,Chen等[6]提出一种新的半监督联合学习框架,通过在联合优化损失函数中集成少量标签信息来学习特征嵌入空间和集群分配。
传统的半监督聚类大多通过对谱聚类、非负矩阵分解和典型相关分析等浅层聚类模型进行改进,或将K-means和线性判别分析(Linear Discriminant Analysis, LDA)等算法进行结合以引入监督信息[7]。但这些方法都属于浅层模型,无法有效表达高维数据间的高层语义信息,如近年来出现的基因信息挖掘,即属于典型的高维数据分析问题。近年来,深度聚类引起了广泛关注,研究者通过学习数据的低维表示,有效缓解传统聚类算法在面对高维输入数据时的退化问题。例如,Yang等[8]提出的深度聚类网络(Deep Clustering Network,DCN)将自动编码器与K-means算法相结合;Peng等[9]提出的深度子空间聚类(Deep Subspace Clustering,DSC)引入一种新颖的自动编码器架构,学习有利于子空间聚类的非线性映射[10]。为了进一步提高高维数据的聚类性能,有研究者提出了一些端到端的深度聚类方法,将深度神经网络(Deep Neural Networks, DNN)融合到聚类中。例如,Xie等[11]在2016年提出的深度嵌入聚类(Deep Embedding Clustering,DEC),可学习数据的聚类特征并以自学习的方式划分数据。Li等[12]在2018年提出的判别提升聚类(Discriminatively Boosted Image Clustering,DBIC)算法使用卷积自动编码器改进DEC,由于该算法使用卷积网络,因此其在图像数据集上的聚类性能优于DEC。
此外,深度聚类算法之所以取得成功有两个重要的因素。首先是深度神经网络强大的特征表示能力以及计算能力,其次是不同的算法在特征学习过程中对特征施加的约束,使得深度神经网络模型在训练过程中学习到更适应于聚类任务的深度特征。尽管深度聚类算法取得了很大的突破,但是很多深度聚类算法在特征学习过程中没有保持特征之间的局部连接结构,导致从原始数据空间到低维特征空间的转换过程中破坏了数据的特征结构,从而产生没有表示意义的特征,在一定程度上影响聚类的性能。
Peng等[13]在基于稀疏先验的深度子空间聚类算法中指出,欠完备自动编码学习样本在嵌入空间中特征表达的同时,保持其在原始空间中的局部结构。受此启发,本文提出基于局部结构保持的改进半监督深度嵌入聚类(Improved Semi-supervised Deep Embedded Clustering, ISDEC)算法。首先,使用欠完备自动编码器建立输入样本及其潜在表示之间的映射关系,从而剔除样本中的不利因素,以及保留数据生成分布的局部结构。其次,将欠完备自动编码器纳入半监督深度嵌入聚类(Semi-supervised Deep Embedded Clustering, SDEC)框架,使该框架可以在保持局部结构的情况下,联合进行聚类和特征表达学习的同步优化。最后,本文采用小批量随机梯度下降(Stochastic Gradient Descent, SGD)和反向传播算法对所提出的ISDEC算法进行优化。
1 半监督深度嵌入聚类半监督深度嵌入聚类(SDEC) [14]从预处理自动编码器开始,然后移除解码器。其余编码器通过优化以下目标进行微调:
| $ \begin{gathered} L=\operatorname{KL}(P \| Q)+\lambda \frac{1}{n} \sum\limits_{i=1}^n \sum\limits_{k=1}^n a_{i k}\left\|z_i-z_k\right\|^2= \\ \underbrace{\sum\limits_{i=1}^n \sum\limits_{j=1}^K p_{i j} \log \frac{p_{i j}}{q_{i j}}}_{L_u}+\underbrace{\lambda \frac{1}{n} \sum\limits_{i=1}^n \sum\limits_{k=1}^n a_{i k}\left\|z_i-z_k\right\|^2}_{L_s}, \end{gathered} $ | (1) |
其中,qij是嵌入点zi和聚类中心μj之间的相似性,由学生t-SNE分布函数测量:
| $ q_{i j}=\frac{\left(1+\left\|z_i-\mu_j\right\|_2^2\right)^{-1}}{\sum\limits_{j' \neq i}\left(1+\left\|z_i-\mu_j^{\prime}\right\|_2^2\right)^{-1}}。$ | (2) |
并且式(1)中的pij是目标分布,定义为
| $ p_{i j}=\frac{q_{i j}^2 / \sum_i q_{i j}}{\sum\limits_{j' \neq i}\left(q_{i j'}^2 / \sum_i q_{i j'}\right)}, $ | (3) |
其中, 矩阵A用来描述成对约束中必须链接约束(Must-Link, ML)和不能链接约束(Cannot-Link, CL),j和j′表示k个聚类中心u的索引, aik是矩阵A的第i行k列的元素。当xi和xk被分配给同一簇时,aik=1。如果xi和xk满足不能链接的约束,aik=-1。此矩阵中的其他元素均为零。
假设f是编码器映射,即zi=f(xi),其中xi是来自数据集X的输入样本。预处理后,可以使用f提取所有嵌入点{zi};然后在{zi}上使用K-means得到初始聚类中心{μj};最后,可以根据式(1)、式(2)和式(3)计算损失L。样本xi的预测标签为
在反向传播期间,梯度∂L/∂zi向下传递,以更新深度神经网络的参数θ。梯度∂L/∂μi用于通过SGD更新聚类中心{μj}j=1K。
2 改进的半监督深度嵌入聚类假设数据集X有n个样本,每个样本xi∈Rn,其中n是维数。初始必须链接约束的集合由ML={(xi, xj):xi和xj属于同一簇}来表示,而不能链接约束的集合是CL={(xi, xj):xi和xj属于不同的簇},1≤i, j≤N。簇数K是先验知识,第j个簇中心由μj∈Rd表示。设si∈{1, 2, …, K}表示分配给样本xi的聚类索引。Z={z1, …, zn}表示它们相应的潜在表示,其中zi=f(xi; θe)∈Rd由编码器学习,编码器的参数由θe定义,d为特征维数。
本文的目标是找到一个好的f,使嵌入点{zi}i=1n更适合于聚类任务。为此,自动编码器是必不可少的。自动编码器用于在无监督的情况下学习表示,学习的特征可以保留数据中固有的局部结构。借用SDEC的聚类损失和成对约束损失负责操纵嵌入空间,以分散嵌入点。整个网络结构如图 1所示。目标定义为
| $ L=L_u+\lambda L_s+\gamma L_r, $ | (4) |
其中, Lr、Lu、Ls分别为重构损失、聚类损失、成对约束损失,λ是由用户定义的权衡参数,γ>0为控制重构程度的参数。当γ=0时,式(4)降为SDEC的目标。
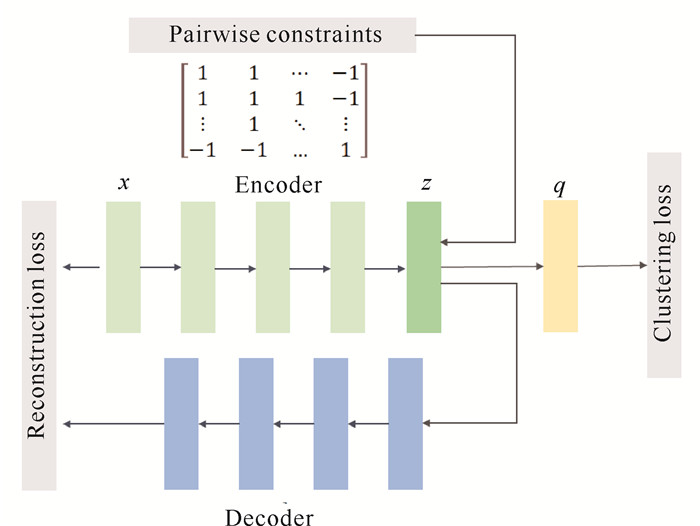
本算法的总体框架如图 1所示,使用预先训练的堆叠自动编码器(Stacked AutoEncoder, SAE)的编码层来初始化DNN结构。将成对约束添加到嵌入层z,以指导特征表示的学习。用重构损失保证嵌入空间保持数据生成分布的局部结构。q表示每个数据点的软分配,并用于计算Kullback-Leibler (KL)发散损失。
|
| 图 1 ISDEC算法框架 Fig. 1 Framework of ISDEC algorithm |
2.1 聚类损失和参数初始化
P和Q之间的KL散度被定义为聚类损失,其中Q为软标签分布, 是通过学生t-SNE分布测量得出,P是从Q推导出来的目标分布。也就是说,聚类损失被定义为
| $ L_u=\operatorname{KL}(P \| Q)=\sum\limits_i \sum\limits_j p_{i j} \log \frac{p_{i j}}{q_{i j}} $ | (5) |
其中, KL用于测量两个概率分布之间的非对称差的散度,通过式(3)和式(2)定义P和Q。
矩阵A设计的思想在于,训练时施加一个约束:将相同类别的点在潜在特征空间中彼此接近,而不同类别的点之间彼此远离。为此,成对约束损失定义为
| $ L_s=\frac{1}{n} \sum\limits_{i=1}^n \sum\limits_{k=1}^n a_{i k}\left\|z_i-z_k\right\|^2 \text { 。} $ | (6) |
按照SDEC中的建议,本文在执行聚类之前对深度编码器进行了预处理。经过预处理后,潜在表示就是原始输入样本在嵌入空间中的有效特征表示。然后采用K-means算法在潜在特征表示上进行聚类中心{μj}j=1K的初始化。
2.2 局部结构保护SDEC获得的嵌入点不一定适用于聚类任务。因为SDEC放弃了解码器,并使用聚类损失Lu和成对约束损失Ls对编码器进行微调。然而,这种微调可能会扭曲嵌入空间,削弱嵌入特征的代表性,从而影响聚类性能。因此,考虑到预训练的潜在特征数据之间的局部连接关系,本节提出在深度特征学习中加入一个局部保持损失函数,用于在网络微调训练的过程中保持预训练特征邻域之间的相似关系。所以,本文利用解码器的输出
| $ L_r=\sum\limits_{i=1}^n\left\|x_i-\widetilde{x}_{z_i}\right\|_2^2, $ | (7) |
其中,zi=f(xi; θe),
为了保证聚类的有效性,用于预处理的堆叠式去噪自动编码器不再适用。因为聚类应该在干净数据的特征上执行,而不是在去噪自动编码器中使用噪声数据,所以本文直接去除噪声,堆叠式去噪自动编码器退化为欠完备自动编码器。
至此,ISDEC算法的总损失函数如下:
| $ \begin{gathered} L=\underbrace{\sum\limits_{i=1}^n \sum\limits_{j=1}^K p_{i j} \log \frac{p_{i j}}{q_{i j}}}_{L_n}+ \\ \lambda \underbrace{\frac{1}{n} \sum\limits_{i=1}^n \sum\limits_{k=1}^n a_{i k}\left\|_{z_i}-z_k\right\|^2}_{L_s}+\gamma \underbrace{\sum\limits_{i=1}^n\left\|x_i-\widetilde{x}_{z_i}\right\|_2^2}_{L_r}, \end{gathered} $ | (8) |
其中,Lu和Ls联合成为SDEC的总体损失函数Lc,用以实现特征数据与聚类中心改进的分配结果,Lr用于保持特征数据从预训练特征空间到微调特征空间的局部结构,使得学习到的特征保持固有本征结构,从而进一步提升特征学习和聚类任务的性能。λ是由用户定义的权衡参数,γ为控制嵌入空间失真程度的系数。
2.3 优化利用小批量梯度下降算法结合反向传播算法最小化目标函数(8),同时对聚类中心μj,以及深度编码器参数θe和θd进行优化。
由于局部保持损失只对特征数据进行约束,而没有涉及聚类中心的计算,因此总体损失函数L对聚类中心μj具有梯度:
| $ \begin{aligned} & \frac{\partial L}{\partial \mu_j}=-2 \sum\limits_{i=1}^n\left(1+\left\|z_i-\mu_j\right\|^2\right)^{-1} \times \\ & \left(p_{i j}-q_{i j}\right)\left(z_i-\mu_j\right)。\end{aligned} $ | (9) |
L损失函数对于特征zi的梯度计算如下:
| $ \begin{gathered} \frac{\partial L}{\partial z_i}=2 \sum\limits_{j=1}^K\left(1+\left\|z_i-\mu_j\right\|^2\right)^{-1} \times \\ \left(p_{i j}-q_{i j}\right)\left(z_i-\mu_j\right)+\frac{2 \lambda}{n} \sum\limits_{k=1}^n a_{i k}\left(z_i-z_k\right)。\end{gathered} $ | (10) |
注意,上述推导来自SDEC。然后给定一个具有m个样本和学习率η的小批量,μj被更新为
| $ \mu_j=\mu_j-\frac{\eta}{m} \sum\limits_{i=1}^m \frac{\partial L}{\partial \mu_j}。$ | (11) |
解码器的权重W′通过以下方式更新:
| $ W^{\prime}=W^{\prime}-\frac{\eta}{m} \gamma \sum\limits_{i=1}^m \frac{\partial L_r}{\partial W^{\prime} }。$ | (12) |
编码器的权重W通过以下方式更新:
| $ W=W-\frac{\eta}{m} \sum\limits_{i=1}^m \frac{\partial L}{\partial W} \text { 。} $ | (13) |
更新目标分布,目标分布P用作“基本事实”软标签,但也依赖于预测的软标签。因此,为避免不稳定,不应仅使用一批数据在每次迭代中更新P。在实践中,本文在每T次迭代中使用所有嵌入点更新目标分布。更新规则见式(2)和式(3)。更新目标分布时,以最大概率的qij为xi的标签计算如下:
| $ s_i=\arg \max\limits_j q_{i j},$ | (14) |
其中, qij由式(2)计算。如果目标分布的两次连续更新之间的标签分配变化(百分比)小于阈值ε,将停止训练。以下算法1总结了整个算法。
算法1:基于局部结构保持的改进半监督深度嵌入聚类
输入:输入数据: X; 聚类数: K; 目标分布更新间隔: T; 停止阈值: δ; 最大迭代: MaxIter。
输出:双自动编码器的权重W和W′;聚类中心μ和标签s。
① 根据3.1节初始化μ、W和W′
② for iter∈{0, 1, …, MaxIter} do
③ if iter%T == 0 then
④ 计算所有嵌入点{zi=fW(xi)}i=1n
⑤ 使用式(2)、式(3)和{zi}i=1n更新P
⑥ 保存上次标签分配: sold=s
⑦ 通过式(14)计算新标签分配s
⑧ if sum(sold≠s)/n < ε then
⑨ 停止训练
⑩ 选择一批样本S∈X
⑪ 通过式(11)、式(12)和式(13)更新S上的μ、W和W′。
3 验证实验 3.1 数据集为了验证所提方法的聚类性能,本文在4个大规模数据集(MNIST、USPS、REUTERS-10K和Fashion-MNIST)和2个基因数据集(LUNG和GLIOMA)上进行实验。MNIST由70 000个28×28像素大小的手写数字组成;USPS包含9 298张灰度图像;REUTERS-10K包含大约810 000个用分类树标注的英语新闻故事[15],本文使用4个根类别:公司/工业、政府/社会、市场和经济作为标签,排除了所有带有多个标签的文档,随机抽样10 000个例子的子集,并计算2 000个最常见单词的tf-idf特征;Fashion-MNIST包含60 000个训练图像和10 000个测试图像,每张图片都以28×28像素的灰度显示。LUNG包含5类共203个样本,每个样本有12 600个基因,去除标准差小于50个表达单元的基因,得到203个样本3 312个基因的数据集;GLIOMA包含4类共50个样本,每个样本有12 625个基因,经过预处理得到了一个包含50个样本和4 434个基因的数据集。
本文以与SDEC相同的方式对除基因数据以外的数据集进行预处理,即对除基因数据以外的所有数据集进行归一化,使得
| 数据集 Dataset |
样本数 Examples |
类别数 Classes |
维数(d) Dimension (d) |
| MNIST | 70 000 | 10 | 784 |
| USPS | 9 298 | 10 | 256 |
| REUTERS-10K | 10 000 | 4 | 2 000 |
| Fashion-MNIST | 70 000 | 10 | 784 |
| LUNG | 203 | 5 | 3 312 |
| GLIOMA | 50 | 4 | 4 434 |
3.2 实验设置
将编码器网络设置为一个全连接的多层感知器(MLP),除基因数据以外的数据集的维数为d-500-500-2 000-10,基因数据由于样本少而特征多,故采用维数为d-1 000-100,其中d为输入数据(特征)的维数。解码器网络的数据集维数与编码器网络的数据集维数是颠倒的,即相应的解码器网络的数据集维数分别为10-2 000-500-500-d和100-1 000-d。深度编码器的所有内层除了输入层、输出层和嵌入层外,所使用的激活函数都是ReLU非线性函数[16]。使用与SDEC相同的参数设置对自动编码器进行预训练和微调,最大限度地减少参数调整的影响,以确保实验结果的改进是本文提出方法的贡献。
对于每个数据集,根据真实标签随机生成成对约束矩阵A。本文从数据集中随机选择两个数据点: 如果两个数据点共享同一个标签,将生成一个必须链接约束;否则,将生成一个不可链接的约束。SGD的学习率为0.01。收敛阈值tol%设置为0.1%。对于所有算法,本文将聚类的数量K设为真实标签类别的数量。参数λ设置为10-5。为了评价聚类结果,本文采用两个标准评价指标: 准确度(ACC)和归一化互信息(NMI)。
本文算法与K-means[1]、深度嵌入聚类(DEC) [5]、成对约束K-means (KM-CST) [17]、改进的深度嵌入聚类(IDEC)[18]、自加权多核学习(SMKL)[10]、半监督深度嵌入聚类(SDEC)[14]算法作聚类性能对比,以此证明本文算法在聚类方面的有效性。
3.3 结果与分析对比方法的结果分别来自对应的论文公开发布的代码,如果某个算法不适用于特定数据集,聚类结果就用N/A代替。由表 2和表 3可以看出,本文所提出的方法优于其他6种先进方法。
| 方法Methods | MNIST | USPS | REUTERS-10K | Fashion-MNIST | LUNG | GLIOMA |
| K-means | 52.98 | 65.67 | 51.62 | N/A | N/A | N/A |
| DEC | 84.35 | 74.08 | 73.68 | 54.75 | 67.98 | 64.00 |
| KM-CST | 54.27 | 68.18 | N/A | N/A | N/A | N/A |
| IDEC | 88.06 | 76.05 | 75.64 | 55.14 | 79.31 | 48.00 |
| SMLK | 78.3 | 68.19 | 72.03 | N/A | N/A | N/A |
| SDEC | 86.11 | 76.39 | 69.37 | 56.85 | 73.39 | 62.00 |
| ISDEC | 94.95 | 78.27 | 74.02 | 65.14 | 81.28 | 70.00 |
| 方法Methods | MNIST | USPS | REUTERS-10K | Fashion-MNIST | LUNG | GLIOMA |
| K-means | 49.74 | 61.5 | 49.32 | N/A | N/A | N/A |
| DEC | 83.72 | 75.29 | 49.76 | 58.21 | 57.64 | 54.82 |
| KM-CST | 50.47 | 63.94 | N/A | N/A | N/A | N/A |
| IDEC | 86.72 | 78.46 | 49.81 | 60.15 | 53.91 | 26.85 |
| SMLK | 68.42 | 71.05 | 40.76 | N/A | N/A | N/A |
| SDEC | 82.89 | 77.68 | 47.62 | 62.76 | 59.77 | 45.56 |
| ISDEC | 88.63 | 80.50 | 57.63 | 63.83 | 63.08 | 51.23 |
具体而言,KM-CST的性能优于K-means,表明结合成对信息提高了聚类性能。与传统的K-means和SMKL相比,深度网络可以学习更具表示能力的特征。虽然DEC和IDEC也利用了数据的深层特征,但它们忽略了隐藏在少量标签数据中的信息。SDEC使用成对约束来指导聚类过程,但没在特征学习过程中保持特征之间的局部连接结构。以上结果表明本算法的局部结构保持与成对约束相结合对聚类的效果有更好的改进作用。
为了进一步说明所提方法的优越性,在图 2中清晰地显示了ISDEC和SDEC在MNIST数据集上训练过程中的准确性,可见ISDEC优于SDEC。

|
| 图 2 ISDEC和SDEC在MNIST训练期间的准确性 Fig. 2 Accuracy of ISDEC and SDEC during MNIST training |
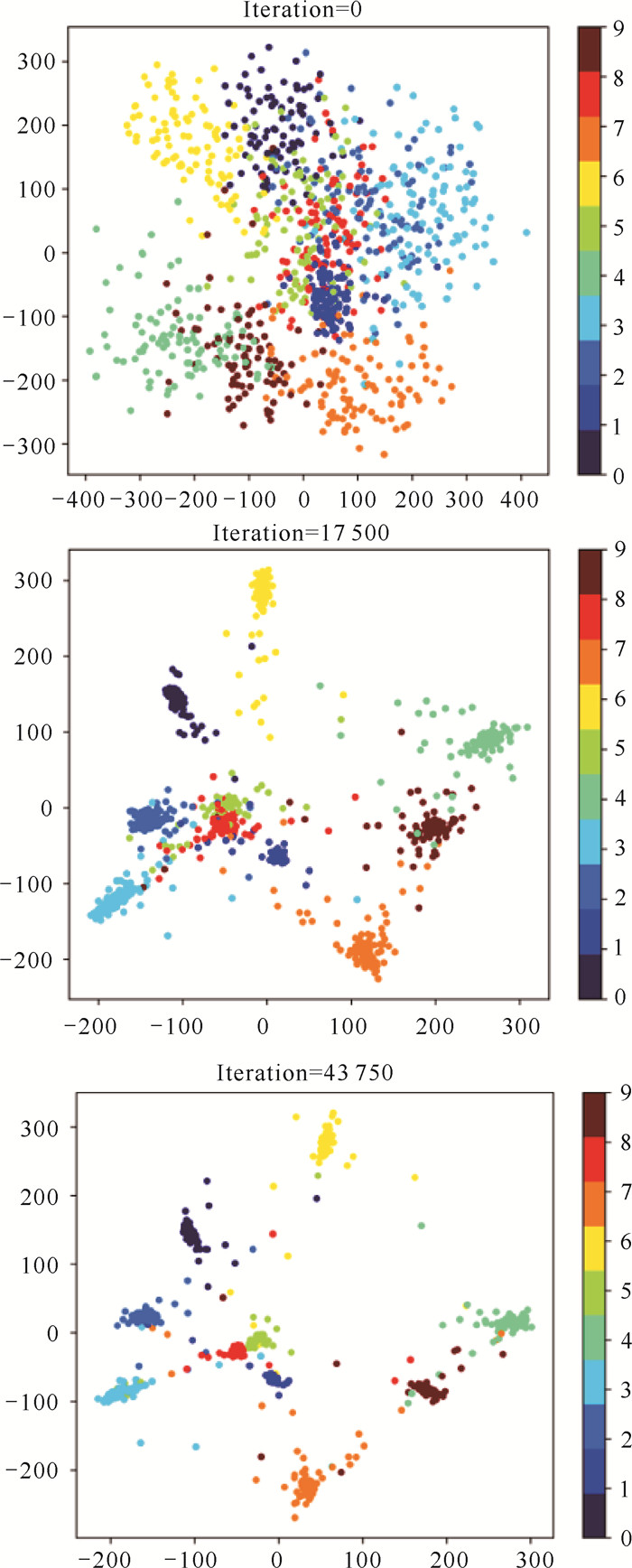
通过在训练过程中对嵌入的特征空间进行可视化,可进一步显示本算法在特征学习过程中的局部保持效果。图 3显示了从MNIST数据集中随机选择1 000个样本的学生t-SNE可视化,并将潜在表示z映射到2D空间。从聚类结果的变化趋势可以看出,随着训练次数的增加,不同簇中的样本更容易区分,同一簇中的样本也更接近,这表明学习到的特征空间更适合聚类任务。
|
| The differences between clusters are shown in different colors 图 3 训练过程中MNIST子集聚类结果的可视化 Fig. 3 Visualization of MNIST sub-cluster class results during training |
4 结论
针对高维数据的半监督聚类问题,本文提出了一种改进半监督深度嵌入聚类(ISDEC)算法,即在现有算法的基础上,着重考虑了高维数据的内在局部保持问题。ISDEC首先通过优化基于KL散度的聚类损失和半监督的成对约束损失来实现数据从原始高维空间到特征空间的映射,并通过引入一个基于自编码的局部保持损失来保持深度特征学习过程中数据表达之间的局部结构。然后,将深度聚类网络融合到一个统一的框架中,对潜在空间的特征进行聚类,从而有效利用样本之间的关系。本文在包括基因数据在内的若干高维数据集上进行了大量的实验研究,定性分析和定量指标都表明,本算法在学习数据的深层特征表达的同时,能有效保持数据的局部结构,从而取得较好的半监督聚类性能。
| [1] |
ANAND S, MITTAL S, TUZEL O, et al. Semi-supervised kernel mean shift clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(6): 1201-1215. DOI:10.1109/TPAMI.2013.190 |
| [2] |
LI H R, ZHANG J S, SHI G, et al. Graph-based discriminative nonnegative matrix factorization with label information[J]. Neurocomputing, 2017, 266: 91-100. DOI:10.1016/j.neucom.2017.04.067 |
| [3] |
杨帆, 王俊斌, 白亮. 基于安全性的成对约束扩充算法[J]. 计算机科学, 2020, 47(9): 324-329. |
| [4] |
李晁铭, 徐圣兵, 郝志峰. 基于成对约束的交叉熵半监督聚类算法[J]. 模式识别与人工智能, 2017, 30(7): 598-608. |
| [5] |
HONG D F, YOKOYA N, XIA G S, et al. X-ModalNet: A semi-supervised deep cross-modal network for classification of remote sensing data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, 167: 12-23. DOI:10.1016/j.isprsjprs.2020.06.014 |
| [6] |
CHEN Z K, LI C J, GAO J, et al. Semisupervised deep embedded clustering with adaptive labels[J]. Scientific Programming, 2021, 2021: 6613452. DOI:10.1155/2021/6613452 |
| [7] |
LV Z H, SONG H B, BASANTA-VAL P, et al. Next-generation big data analytics: State of the art, challenges, and future research topics[J]. IEEE Transactions on Industrial Informatics, 2017, 13(4): 1891-1899. DOI:10.1109/TII.2017.2650204 |
| [8] |
YANG B, FU X, SIDIROPOULOS N D, et al. Towards k-means-friendly spaces: Simultaneous deep learning and clustering[C]// Proceedings of the 34th International Conference on Machine Learning. Sydney, Australia: JMLR, 2017: 3861-3870.
|
| [9] |
PENG X, FENG J S, ZHOU J T, et al. Deep subspace clustering[J]. IEEE Transactions on Neural Networks and Learning Systems, 2020, 31(12): 5509-5521. DOI:10.1109/TNNLS.2020.2968848 |
| [10] |
VIDAL R. Subspace clustering[J]. IEEE Signal Pro- cessing Magazine, 2011, 28(2): 52-68. DOI:10.1109/MSP.2010.939739 |
| [11] |
XIE J Y, GIRSHICK R, FARHADI A. Unsupervised deep embedding for clustering analysis[C]// Proceedings of the 33rd International Conference on Machine Learning. New York, USA: JMLR, 2016: 478-487.
|
| [12] |
LI F F, QIAO H, ZHANG B. Discriminatively boosted image clustering with fully convolutional auto-encoders[J]. Pattern Recognition, 2018, 83: 161-173. DOI:10.1016/j.patcog.2018.05.019 |
| [13] |
PENG X, XIAO S J, FENG J S, et al. Deep subspace clustering with sparsity prior[C]// Proceedings of the 25th International Joint Conference on Artificial Intelligence. New York, USA: AAAI Press, 2016: 1925-1931.
|
| [14] |
REN Y Z, HU K R, DAI X Y, et al. Semi-supervised deep embedded clustering[J]. Neurocomputing, 2019, 325: 121-130. DOI:10.1016/j.neucom.2018.10.016 |
| [15] |
LEWIS D D, YANG Y M, ROSE T G, et al. RCV1:A new benchmark collection for text categorization research[J]. Journal of Machine Learning Research, 2004, 5: 361-397. |
| [16] |
GLOROT X, BORDES A, BENGIO Y. Deep sparse rectifier neural networks[C]// Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. Fort Lauderdale, USA: JMLR, 2011: 315-323.
|
| [17] |
BASU S, BANERJEE A, MOONEY R J. Active semi-supervision for pairwise constrained clustering[C]// Proceedings of the 2004 SIAM International Conference on Data Mining. Lake Buena Vista, Florida, USA: [S. n. ], 2004: 333-344.
|
| [18] |
GUO X F, GAO L, LIU X W, et al. Improved deep embedded clustering with local structure preservation[C]// Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne, Australia: IJCAI, 2017: 1753-1759.
|



