随着软件工程、智能计算机、通讯技术及观测仪器设备的迅猛发展,海洋观测系统建设取得了很大的进展,显著提高了海滨观测自动化水平。海洋观测系统最重要的特征是通过网络技术连接不同地理位置的智能传感器设备,从而实现观测数据实时监测和海洋资源共享。海洋观测设施包括水文气象自动观测、测波雷达、海啸预警装置及在线监测浮标等,要素涵盖潮汐、海温、盐度、风、气压、气温、相对湿度、海面有效能见度、降水量、GPS高程、pH值、溶解氧及叶绿素等[1]。由于海洋数据具有海量性、多样性、不可重复观测等特点,仅凭观测值班员人工校对往往不能及时发现数据质量问题。因此,利用计算机对实时数据流进行自动监控和异常报警十分重要。
近年来,围绕海洋数据质量监控问题,国外开展了一系列研究。例如,Koziana等[2]基于美国浮标系统,通过阈值准则判断数据质量,实现观测数据异常检测自动化;Morello等[3]在延时模式下,从时间、空间、阈值、变化率等多个角度出发,对澳大利亚海洋观测系统原始数据进行质量监控;Gurgel等[4]利用最小乘法多项式拟合算法,对德国湾沿岸观测系统的雷达电流场数据进行质量检查,并在此基础上合成二维电流图;Kim等[5]通过比较样本组间/组内余弦相似性、曼哈顿距离、欧氏距离、余弦相似角距离等10余种指标,分析数据一致性,进而确定高维数组中的异常值;Mohammadi等[6]从大数据和流数据两个角度出发,探讨深度神经网络在物联网中的应用。
放眼国内,相关研究成果也层出不穷。例如,史静涛[7]对比极值算法、3σ检验法、格拉布斯算法、Dixon算法等异常检测算法,以散点图、曲线图的形式展现异常数据剔除后的效果,得到不同异常检测算法的适用条件,并应用于海洋观测系统;温玉波[8]从数据管理的角度研究数据质量监控方法,利用计算机程序对观测数据记录的相符性、合理性、相关性以及分布拟合性进行检验,提升质量监控效率;丁君生等[9]基于183个测点近十年的全球卫星导航系统(GNSS)观测数据,综合考虑数据量、网格分辨率、模型稳定性等因素进行异常检测,实现对流层天顶总延迟的精细建模。然而,纵观国内外相关文献资料和产品应用可以发现,诸多研究主要围绕延时数据(月报、年报等)的异常检测,针对海洋观测实时数据的异常检测问题研究较少。而立体监测网建立后,巨量观测数据已使得人工观测校对难以实现[10],应用实时大数据质量监控算法,精细化海洋观测数据质量管理迫在眉睫。
鉴于以上讨论,为了在复杂的海洋环境下进行异常检测,本文使用无监督学习算法进行异常检测:基于层级实时记忆(Hierarchical Temporal Memory,HTM)网络[11],将复杂的非马尔可夫环境下的观测数据异常检测问题转化为模式匹配与预测,对单源传感器数据进行异常检测;利用分布于不同测点、相同观测要素传感器之间的数据相关性,构建基于多源传感器数据的异常检测模块,提高算法异常检测能力;应用沿海岸段水文气象观测站点实测数据进行异常检测实验,通过漏报率与误报率两个指标,验证本算法的有效性和实时性;利用贝叶斯在线变点检测、相对熵、高斯滑动窗口算法进行异常检测实验,比较和分析各类算法异常检测结果。
1 海洋观测系统海洋测点分布于不同地理位置,每个测点部署一套智能传感器组,用于采集各类海洋要素的观测值,常用的海洋观测传感器包括温度计、盐度计、水位计、气压表、能见度仪、雨量筒和风速风向仪等,数据采集模块汇总各类传感器信号并转化成数字量,通过无线网络、光纤、卫星等方式发往数据中心进行数据处理及存储。定义实时数据矩阵为Yt={ytn, m},ytn, m表示在当前t时刻下由测点n的m类传感器采样得到的实时观测数据。
数据中心接收到各测点传感器采集的实时观测值Yt后再做数据预处理,然后利用算法进行异常检测,将不符合观测要素时空特征和站点间相关性的数据标记为异常,海洋观测网框架如图 1所示。
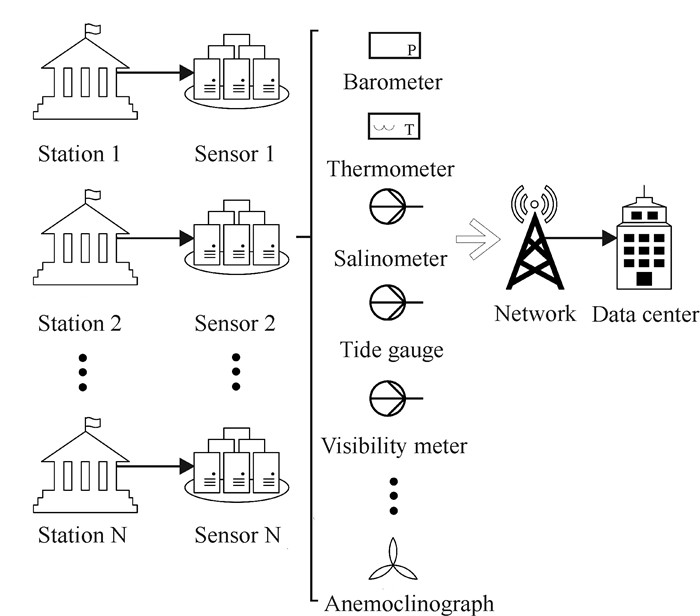
|
| 图 1 海洋观测网框架图 Fig. 1 Frame diagram of marine observation network |
常见的观测数据异常现象如图 2所示。其中图 2(a)的异常现象表示潮位数据长时间不变,该现象通常由验潮井淤积、连通管被生物附着或泥沙堵塞引起,需要及时清理运维;图 2(b)的异常现象表示由温度计故障引起的温度值异常和突变。
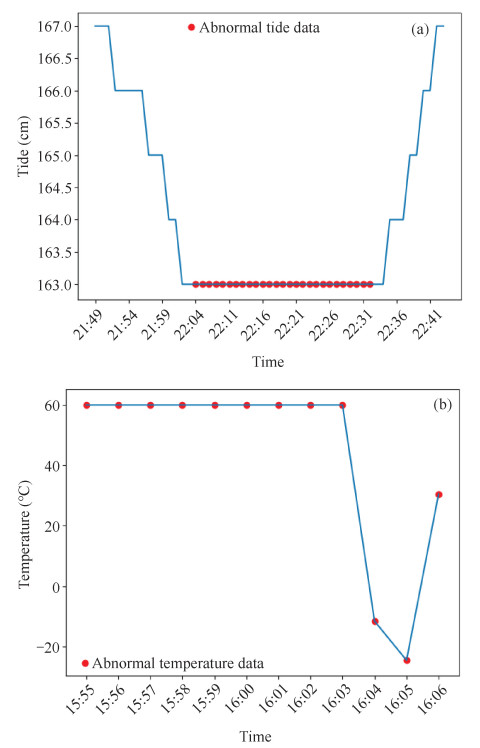
|
| 图 2 潮位和温度数据异常 Fig. 2 Abnormal of tide and temperature data |
本文考虑到海洋观测网中数据的丢包和缺测现象,故设计符合实际应用需求的异常检测算法,对接收到的实时观测数据进行异常检测,发现数据空间相关性、时间相关性、多源相关性等异常并进行标记,进而定位故障传感器。
2 异常检测算法HTM网络是模拟新大脑皮质层神经活动的一种新型机器学习算法,能够处理流式时间序列。该算法的优点体现在无须调整参数、在线学习和鲁棒性强。在此基础上,利用多源传感器数据,基于距离相关性对离群点进行检测,进一步减少异常值的漏报率。
2.1 数据预处理由于网络传输数据存在丢包[12]、时延[13]等通信约束,并且传感器采集数据存在缺测问题,因此异常检测之前需要对数据进行预处理,将超时未收到实测数据的传感器标记为异常,并且根据《海洋观测规范:第2部分海滨观测》(GB/T 14914.2-2019)[14]标记缺测数据为异常,标记为异常的数据不进行后续的HTM网络学习识别和距离检测。接着,将处理好的高质量数据输入到HTM网络模块进行计算分析。
2.2 单源数据异常检测 2.2.1 HTM架构HTM网络每一层都有大量的神经元,通过学习不断更新突触连通值,建立符合观测数据时间和空间特征的模型,HTM网络架构如图 3所示。
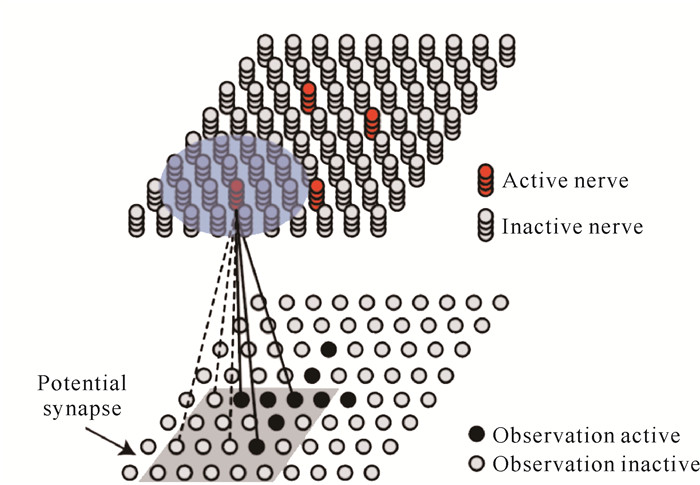
|
| 图 3 HTM网络架构图 Fig. 3 Network architecture diagram of HTM |
HTM网络的主要组成部分如下。①神经元。神经元是负责传输信息的细胞,由观测输入激活进入活跃状态,由横向输入(其他神经元输入)刺激进入预测状态。②神经柱。多个神经元堆叠成一个神经柱,同一个神经柱的神经元共享观测输入的激活信号。③前馈树突。每个神经元有一个前馈树突,产生动作电位进而激活神经元进入活跃状态。④末端树突。每个神经元有多个末端树突,刺激神经元去极化进入预测状态。⑤突触。前馈树突和末端树突上分布着大量突触,前馈突触由观测输入的稀疏离散表征激活,末端突触由其他神经元输入激活。当突触连通值小于阈值时,处于非连通状态,称为潜在突触。反之,当突触连通值大于阈值时,处于连通状态,称为连通突触。
2.2.2 神经元学习步骤① 初始化。初始化HTM网络,设置神经柱数量、神经柱内所含神经元数量、树突激活阈值、突触连通阈值等参数,随机初始化突触连通值。
② 计算神经柱激活状态。根据当前观测输入得到神经柱激活状态,具体计算公式如下:
| $ a_t^i= \\ \left\{\begin{array}{l} 1, b^i \tilde{V}^i Z^i \geqslant \operatorname{sort}\left(\left\{b^o \tilde{V}^o Z^o\right\}, k\right) \text { 且 } b^i \tilde{V}^i Z^i>\theta_a, \\ 0, \text { 其他 } \end{array}\right. $ | (1) |
其中,ati表示在当前时刻t下第i个神经柱的活跃状态,0表示非活跃,1表示活跃;o表示抑制域半径φ内的神经元;Ṽi表示第i个神经柱的前馈突触状态,0表示非活跃,1表示活跃;Zi表示第i个神经柱接收到的观测输入ytm, n的稀疏离散表征[15];θa表示神经柱激活阈值;bi表示第i个神经柱的连通增益;sort({·}, k)表示{·}中元素从大到小排序后的第k个值。
式(1)表示,一个神经柱被激活,不仅要满足由当前输入激活的突触数量乘以增益bi大于阈值θa,还需满足在当前抑制域半径φ内数值排名大于k,这样可以避免琐碎和多余的表征,同时保证活跃神经柱的稀疏性。
连通增益bi和活跃状态神经柱上的前馈突触连通值Vi更新公式如下:
| $ b^i=\exp \left(-\beta\left(\frac{(T-1) * \bar{a}_{t-1}^i+\bar{a}_t^i}{T}\right)\right), $ | (2) |
| $ V^i=q^{+}\left(V^{i, j} \odot A_{t-1}\right)-q^{-}\left(V^{i, j} \odot\left(I-A_{t-1}\right)\right), $ | (3) |
其中,T表示设置的平均周期;At-1={at-1i}表示神经柱活跃矩阵;ati表示第i个神经柱从当前时刻t到t-T+1时刻的活跃状态均值;at-1i表示第i个神经柱从上一时刻t-1到t-T时刻的活跃状态均值;参数q+表示对激活神经柱突触对应连通性的提升,参数q-表示对非激活神经柱突触对应连通性的抑制;⊙表示矩阵点乘运算。
③ 计算神经元激活状态。当神经元处于激活神经柱中,且在前一时刻下处于预测状态,则激活该神经元;或者所处激活神经柱中所有神经元都不处于预测状态,则神经柱上的所有神经元均被激活,具体计算公式如下:
| $ a_t^{i, j}=\left\{\begin{array}{l} 1, j \in A_t \text { 且 } \pi_{t-1}^{i, j}=1 \\ 1, j \in A_t \text { 且 } \sum _i \pi_{t-1}^{i, j}=0, \\ 0, \text { 其他 } \end{array}\right. $ | (4) |
其中,πt-1i, j表示上一时刻t-1下第i个神经柱中的第j个神经元的预测状态,0表示不处于预测状态,1表示处于预测状态;ati, j表示在当前t时刻下第i个神经柱中的第j个神经元的活跃状态,0表示非活跃,1表示活跃。
④ 计算神经元预测状态。根据当前神经元激活状态及突触活跃状态,更新神经元预测状态,具体计算公式如下:
| $ \pi_t^{i, j}=\left\{\begin{array}{l} 1, \exists_u\left\|\tilde{U}_u^{i, j} \odot A_t\right\|_1>\theta_p, \\ 0, \text { 其他 } \end{array}\right. $ | (5) |
其中,θp表示预测状态激活阈值;At={ati, j}为神经元活跃矩阵,Ũui, j表示第i个神经柱中的第j个神经元的第u个末端树突上的突触状态,0表示非活跃,1表示活跃。
⑤ 更新末端突触连通度。获取上一时刻预测正确的神经元,具体计算公式如下:
| $ U_1=\left\{U_u^{i, j} \mid \pi_{t-1}^{i, j}=1 \text { 且 } a_t^{i, j}=1\right\} \text {, } $ | (6) |
其中,U1表示预测成功(上一时刻t-1下处于预测状态的神经元在当前时刻t下被成功激活)的神经元。
当输入激活的神经柱中不存在处于预测状态的神经元,则需要选择其中一个神经元来替代,这里选择末端树突上突触活跃数目最大的神经元:
| $ \begin{aligned} & U_2=\left\{\tilde{U}_u^{i, j} \mid \underset{i, j}{\operatorname{argmax}}\left(\left\|\quad \tilde{U}_u^{i, j} \odot A_t\right\|\right)\right. \text { 且 } \\ & \left.\forall_{i \in A_t}\left(\sum \pi_{t-1}^{i, j}=0\right)\right\}。\end{aligned} $ | (7) |
HTM网络只更新处于活跃状态的神经元突触连通度,因此得到需要更新的突触集合为
| $ U=U_1+U_2 \text { 。} $ | (8) |
突触连通值更新依据赫布法则:奖励激活神经元突触,抑制非激活神经元突触。
| $ U_u^{i, j}=U_u^{i, j}+\Delta U_u^{i, j}, $ | (9) |
上式为连通度变化公式,其中变化量ΔUui, j为
| $ \Delta U_u^{i, j}= \\ \left\{\begin{array}{l} p^{+}\left(U_u^{i, j} \odot A_t\right)-p^{-}\left(U_u^{i, j} \odot\left(I-A_t\right)\right), a_t^{i, j}=1 \\ p^{--} U_u^{i, j}, a_t^{i, j}=0 \text { 且 } \pi_t^{i, j}=1 \end{array}, \right. $ | (10) |
其中,参数p+表示对激活神经元突触对应连通性的提升,参数p-表示对非激活神经元突触对应连通性的抑制。另外,引入参数p- -来模拟抑制域,且p- -<< p-。
⑥ 异常判断。比较HTM网络预测与观测输入的差异程度:
| $ f_t=\frac{\left|A_t-\left(\Pi_{t-1} \cap A_t\right)\right|}{\left|A_t\right|},$ | (11) |
其中,ft为当前时刻t下的异常分数,At表示当前时刻t下的活跃神经元,Πt-1表示在前一时刻t-1下处于预测状态的神经元。
定义当前时刻t下由HTM网络检测得到的异常标签集合Ht={htn, m},其中htn, m表示当前时刻t下测点n中的m类传感器异常标签,0代表数据正常,1代表数据异常,判断方法为
| $ h_t^{n, m}=\left\{\begin{array}{l} 1, f_t>\varepsilon \\ 0, \text { 其他 } \end{array}, \right. $ | (12) |
其中,ε为设置的异常阈值,大小介于0和1之间。
2.3 多源数据异常检测由于HTM网络是无监督学习过程,可以有效检测出未曾出现过的增减趋势、变化频率和数据点等异常。但当某类异常持续时间和发生频率趋于常态化后,HTM网络将适应异常规律,将异常现象判断为正常。为了提高算法异常检测的准确率,本文在HTM网络的基础上,利用不同测点同类观测要素测量值之间的数据相关性进行异常检测,具体步骤如下。
① 设置距离阈值。各测点观测时序数据可以看成是某空间下的点,在同一空间下进行多源数据异常检测时,需要找到一个距离度量,即给出空间下两点之间的距离。定义实时观测数据ytn, m与其他测点同类传感数据之间的距离Dtn, m={dtη, n, m},dtη, n, m表示测点n的m类传感器测量值与测点η的m类传感器测量值之间的距离,则
| $ d_t^{\eta, n, m}=\left\|y_t^{\eta, m}-y_t^{n, m}\right\|, $ | (13) |
该距离测度须满足以下条件[8]:dtη, n, m>0(非负性);dtη, n, m=dtn, η, m(对称性);dtη, n, m≤dtμ, n, m+dtμ, η, m(三角不等式)。根据历史观测数据,可得测点n的m类传感器观测值与其他各个测点m类传感器观测值的距离阈值为Λn, m={Δη, n, m|∀η≠n }。其中,Δη, n, m表示测点n中的m类传感器测量值与测点η的m类传感器测量值之间的距离阈值。
② 异常判断。定义异常标签为Rtn, m={rtη, n, m},rtη, n, m表示当前时刻t下测点n中的m类传感器测量值与测点η的m类传感器测量值之间距离的异常标签,1表示异常,0表示正常,判断方法为
| $ r_t^{\eta, n, m}=\left\{\begin{array}{l} 1, d_t^{\eta, n, m}>\Delta^{\eta, n, m} \\ 0, \text { 其他 } \end{array}\right. \text { 。} $ | (14) |
传感器异常的判断方法如下:
| $ R_t^{n, m}=\left\{\begin{array}{l} 1, \sum _\eta r_t^{\eta, n, m}>\operatorname{ceil}(N / 2), \\ 0, \text { 其他 } \end{array}, \right. $ | (15) |
上式表示,在当前时刻t下某个传感器与其他测点同类传感器数据相关性的异常标签数量超过传感器总数N的一半时,判断该传感器数据ytn, m异常。
③ 融合算法。结合2.2小节中HTM网络得到的异常标签htn, m,计算最终异常标签St={stn, m}为
| $ s_t^{n, m}=\left\{\begin{array}{l} 1, h_t^{n, m}=1 \text { 或 } R_t^{n, m}=1 \\ 0, \text { 其他 } \end{array}\right. \text {, } $ | (16) |
上式表示, HTM网络的异常标签与距离检测的异常标签取并集,综合单源数据时空异常和多元数据相关性异常,基于HTM网络的多源实时数据异常检测算法流程如图 4所示。
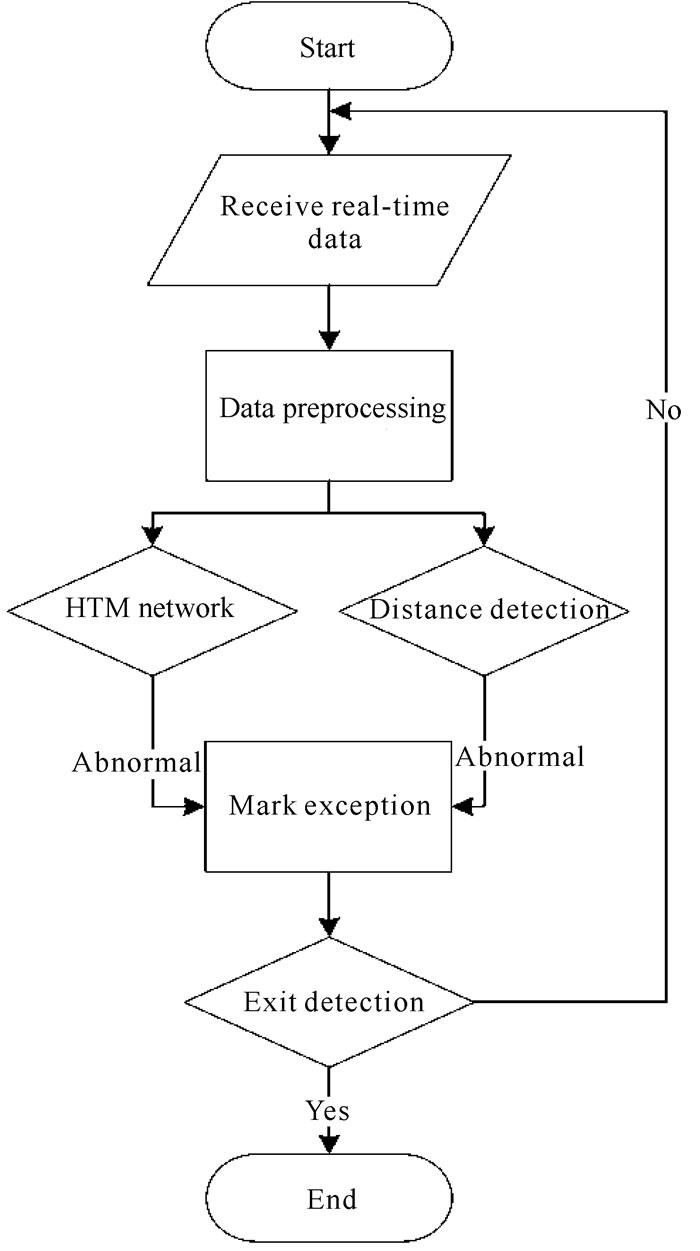
|
| 图 4 算法流程图 Fig. 4 Flow chart of algorithm |
3 实验与结果分析 3.1 实验环境
硬件环境:联想计算机,Inter Core i7-9700处理器,8 GB内存,1 T硬盘。软件环境:Windows10 64位操作系统,Python2.7程序语言,PyCharm开发平台,nupic算法库。实验数据:沿海岸段3个海洋测点实测潮位及温度数据,潮位数据由SCALL-3A浮子式水位计采集,温度数据由HMP155温度计采集,数据时间跨度为2个月,采集频率均为每分钟1个,数据概况如表 1所示。
| 位置 Location |
传感器 Sensor |
条数 Number |
丢包 Packet loss |
缺测 Data miss |
| Location 1 | Tide gauge | 86 652 | 1 188 | 11 |
| Location 2 | Tide gauge | 87 212 | 628 | 2 |
| Location 3 | Tide gauge | 87 590 | 250 | 8 |
| Location 3 | Thermometer | 87 795 | 45 | 77 |
3.2 算法参数
HTM网络参数:神经柱数量为2 048个, 神经柱内神经元数量为32个, 周期T为1 000, 激活状态阈值θa为13, 抑制域半径φ为64, 抑制域内活跃神经柱数量约束k为40, 前馈突触连通阈值为0.2, 前馈突触连通增益q+为0.003, 前馈突触连通抑制q-为0.000 5, 预测状态阈值θp为10, 末端突触连通阈值为0.5, 末端突触连通增益p+为0.1, 末端突触连通抑制p-为0.1, 异常阈值ε为0.9。
距离检测模块参数:测点1,2,3的水位计测量值与其他测点水位计测量值的正常距离阈值分别为Λ1, 1={342, 321}、Λ2,1={342, 344}和Λ3,1={321, 344},测点3中的温度计测量值与测点1、测点2温度计测量值的正常距离阈值为Λ3, 2={10.8, 11.5}。
3.3 结果与分析异常检测结果评价指标:①漏报(False Positive, FP),实际为异常但算法检测为正常的数量;②误报(False Negatives, FN),实际为正常但算法检测为异常的数量。
本文算法与未预处理数据的HTM网络(没有清理缺测数据)、HTM网络(没有进行多源数据检测)的异常检测结果如表 2所示。从结果可以看出,未进行数据预处理的异常检测结果最差,由于未清理缺测数据999.8,9 998[14],导致HTM网络将缺测数据附近的正常数据标记为异常,误报数目较大。未进行距离检测的异常结果由于没有考虑多源数据距离相关性,只能检测出单源数据异常,因此漏报数目较大。而本文算法综合考虑了单源观测数据时空特征及多源观测数据的距离相关性,其中误报多数是在HTM网络识别学习初期产生的,后期产生的误报数很少。
| 位置 Location |
传感器 Sensor |
本文算法 Algorithm of this paper |
未预处理数据的HTM网络 HTM network without preprocessing data |
HTM网络 HTM network |
|||||
| 漏报FP | 误报FN | 漏报FP | 误报FN | 漏报FP | 误报FN | ||||
| Location 1 | Tide gauge | 0 | 3 | 77 | 6 | 75 | 3 | ||
| Location 2 | Tide gauge | 2 | 3 | 35 | 4 | 34 | 3 | ||
| Location 3 | Tide gauge | 0 | 3 | 1 | 6 | 0 | 3 | ||
| Location 3 | Thermometer | 2 | 5 | 107 | 5 | 19 | 5 | ||
为验证本文算法的有效性,将本文算法与贝叶斯在线变点检测[16]、相对熵[17]、高斯滑动窗口算法实时观测数据异常检测结果进行比较,结果如表 3所示。结果表明,基于HTM网络的多源异常检测算法具有较低的漏报数目,整体异常检测效果更佳。
| 位置 Location |
传感器 Sensor |
贝叶斯在线变点检测 Bayes online changepoint detection |
相对熵 Relative entropy |
高斯滑动窗口 Gaussian slide window |
|||||
| 漏报FP | 误报FN | 漏报FP | 误报FN | 漏报FP | 误报FN | ||||
| Location 1 | Tide gauge | 105 | 9 | 112 | 0 | 102 | 1 | ||
| Location 2 | Tide gauge | 34 | 2 | 35 | 0 | 34 | 1 | ||
| Location 3 | Tide gauge | 3 | 0 | 7 | 0 | 0 | 1 | ||
| Location 3 | Thermometer | 118 | 56 | 117 | 2 | 31 | 51 | ||
基于本文算法、未预处理数据的HTM网络、HTM网络、贝叶斯在线变点检测、相对熵、高斯滑动窗口对异常温度数据段的检测结果如图 5所示。从图中可以看出,未预处理数据的HTM网络不能识别出异常点,而HTM网络识别出1个异常点,贝叶斯在线变点检测出1个异常点,相对熵检测出1个异常点,高斯滑动窗口检测出6个异常点,而本文算法检测出11个(全部)异常点,在实际应用中具有较高的异常检测性能。从异常检测的效率来看,本文算法识别一条数据的时间约为4 ms,观测传感器采集周期一般为1 min,能满足海洋观测网中异常检测的实时性需求。
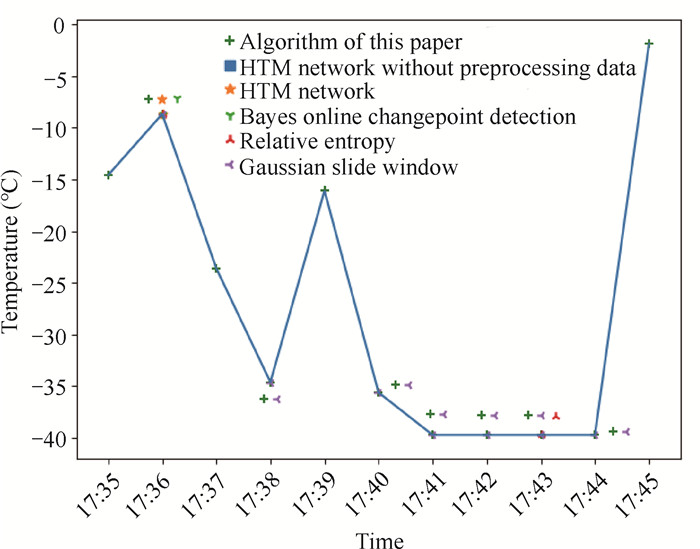
|
| 图 5 异常检测结果 Fig. 5 Abnormal detection results |
4 结论
本文聚焦海洋实时观测数据的异常检测问题,考虑数据缺测和丢包现象,应用HTM网络对观测数据时序序列的内在关系进行模拟,实现基于单源数据的质量监控,同时利用不同地理位置的同类传感器数据,进行基于距离的多源数据异常检测。测点实测数据结果表明,本文设计的算法有良好的异常检测表现,并且能适应网络丢包、数据缺测等现象,具有较强的鲁棒性。目前,HTM网络的异常检测对象为单变量,对于传感器数量较多的网络需要并行部署多台计算机,以满足异常检测的实时性需求,如何将检测对象转化为多变量进行学习识别是未来的研究方向之一。此外,结合其他数据相关性(站点内传感器数据相关性的异常检测)是另一个重要的研究方向。
| [1] |
刘岩, 王昭正. 海洋环境监测技术综述[J]. 山东科学, 2001, 14(3): 30-35. |
| [2] |
KOZIANA J V, OLSON J, ANSELMO T, et al. Automated data quality assurance for marine observations[C]//OCEANS 2008 Conference. Quebec, Canada: IEEE, 2008: 700-705.
|
| [3] |
MORELLO E B, LYNCH T P, SLAWINSKI D, et al. Quantitative quality control (QC) procedures for the Australian national reference stations: Sensor data[C]//Oceans'11 MTS/IEEE KONA. Waikoloa, Hawaii, USA: IEEE, 2011: 19-22.
|
| [4] |
GURGEL K W, SCHLICK T, VOULGARIS G, et al. HF radar observations in the German bight: Measurements and quality control[C]//2011 IEEE/OES 10th Current, Waves and Turbulence Measurement, Monterey. California, USA: IEEE, 2011: 51-56.
|
| [5] |
KIM G T, KIM Y K, KWON M S, et al. Quality control plot for high dimensional omics data[C]// 2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). Shenzhen, China: IEEE, 2016: 15-18.
|
| [6] |
MOHAMMADI M, AL-FUQAHA A, SOROUR S, et al. Deep learning for IoT big data and streaming analytics: A survey[J]. IEEE Communications Surveys and Tutorials, 2018, 20(4): 2923-2960. DOI:10.1109/COMST.2018.2844341 |
| [7] |
史静涛. 海洋环境实时观测数据质量控制方法研究与软件实现[D]. 天津: 国家海洋技术中心, 2010.
|
| [8] |
温玉波. 海洋环境观测数据的质量控制研究[J]. 农业网络信息, 2014(2): 35-38. |
| [9] |
丁君生, 陈俊平, 王君刚. GNSS观测数据ZTD建模的质量控制方法[J]. 宇航学报, 2020, 41(9): 1195-1203. |
| [10] |
邹国良, 韩金菊, 屠正飞, 等. 基于BP神经网络的海洋监测数据等级划分[J]. 海洋通报, 2016, 35(2): 187-193. |
| [11] |
AHMAD S, LAVIN A, PURDY S, et al. Unsupervised real-time anomaly detection for streaming data[J]. Neurocomputing, 2017, 262(1): 134-147. |
| [12] |
FENG Y, CHEN X, GU G X. Output feedback stabilization for discrete-time systems under limited communication[J]. IEEE Transactions on Automatic Control, 2017, 62(4): 1927-1932. |
| [13] |
黄凌云, 洪卫星, 谢可心, 等. 具有两类时延的离散时间多智能体系统一致性跟踪[J]. 广西科学, 2017, 24(6): 573-577. |
| [14] |
国家市场监督管理总局, 中国国家标准化管理委员会. 海洋观测规范: 第2部分海滨观测: GB/T 14914.2-2019[S]. 北京: 中国标准出版社, 2019.
|
| [15] |
曾惟如, 吴佳, 闫飞. 基于层级实时记忆算法的时间序列异常检测算法[J]. 电子学报, 2018, 46(2): 325-332. |
| [16] |
PAN Y J, ZHENG Z Y. Bayesian online change point detection method for process monitoring[C]//Proceedings of 2020 Chinese Control and Decision Conference (CCDC). Hefei, China: IEEE, 2020: 3389-3393.
|
| [17] |
WANG C W, VISWANATHAN K, CHOUDUR L, et al. Statistical techniques for online anomaly detection in data centers[C]//IFIP/IEEE International Symposium on Integrated Network Management. Dublin, Ireland: IEEE, 2011: 385-392.
|



