2. 南宁学院,广西中国-东盟综合交通国际联合重点实验室,广西南宁 530200
2. Guangxi Key Laboratory of International Join for China-ASEAN Comprehensive Transportation, Nanning University, Nanning, Guangxi, 530200, China
随着无线通信技术的快速发展,越来越多的移动设备有了无线网络访问需求。虽然将计算密集型应用卸载到云端可以克服移动设备资源受限的弊端,但是对于时延敏感型应用而言,移动设备与云端的无线网络连接带来的较长延时却并不能使用户满意[1]。移动边缘计算(Mobie Edge Computing, MEC)将计算节点布置到网络边缘,可以满足用户低时延的需求。当前MEC中的计算卸载技术主要包括卸载决策、资源分配和卸载系统实现等3个方面,其中卸载决策主要解决的是移动终端决定如何卸载、卸载多少以及卸载什么的问题[2]。该类研究主要集中于考虑多用户环境和多服务器环境下的卸载决策问题[3, 4]。
目前,一些研究人员利用粒子群优化(Particle Swarm Optimization, PSO) 算法来解决计算卸载问题。Wei等[5]采用基于贪心策略的PSO算法和动态PSO算法,提出了基于动态PSO算法的单用户多边云设备任务分配策略,考虑了任务的相互依赖性。Bi等[6]使用基于遗传模拟退火和PSO的启发式算法来解决非线性约束优化问题,联合优化了每个移动设备的任务卸载比、CPU速度和传输功率,以及可用通道的带宽,进而实现更低能耗。Li等[7]建立了时延、能耗和多目标优化模型,增加了平衡延迟和能量消耗的惩罚函数,提出了改进PSO算法的卸载策略(Improved Optimization Algorithm based on Particle Swarm, EIPSO)。Al-Habob等[8]则考虑了一组需要调度到服务器的相互依赖的子任务,并基于遗传算法和冲突图模型解决了调度问题,使卸载延迟和失效概率最小化。罗斌等[9]对边缘云的MEC服务器进行编码,最后通过PSO算法确定每个任务对应的服务器编号,实验结果表明,该算法使系统总成本降低了20%。缪裕青等[10]引入压缩因子,并运用模拟退火算法思想改进PSO算法,以此实现任务卸载,其中粒子的编码对应车辆任务分配方案,仿真结果表明其代价是传统PSO算法的53.8%。
也有研究人员在计算卸载时采用缓存技术来提高优化效果,如利用移动边缘缓存将内容放置在用户边缘,这样可以有效降低用户请求延迟和能耗,并且避免数据通过回程链路传输,从而降低回程流量[11]。郭煜[1]将任务缓存与卸载决策最优化问题分为两个子优化问题,任务卸载策略可转变为凸最优化问题,通过内点法求解;任务缓存可转变为0-1整数规划问题,使用分支限界法获取最优解,仿真实验表明该策略在动态异构的任务执行环境下可以实现更好的能效优化。Nath等[12]开发了一种基于深度学习的动态调度策略,该策略将流行任务缓存到MEC服务器中避免重复卸载,以此最小化代价函数的长期平均值。Lan等[13]利用随机理论提出了一个任务缓存优化问题,并采用基于遗传算法的任务缓存算法进行求解。
分析以上的研究工作可以发现,对于MEC场景中基于PSO算法的计算卸载问题,现有的工作大多集中在粒子编码或融合其他算法的研究上,从时延或能效优化的角度对算法优劣进行评估。此外,与其他算法结合的PSO算法的优化结果优于传统算法,且加入任务缓存策略的卸载比无缓存的卸载时延的优化更胜一筹。基于此,本文提出一个基于遗传-粒子群优化算法(Genetic-Particle Swarm Optimization Algorithm, GA-PSO)和缓存机制的卸载策略,在边缘云上进行缓存,以便有效降低移动边缘计算的时延。最后通过仿真实验,证明所提算法的收敛性和有效性。
1 系统模型本文研究的目标是在边缘云缓存能力受限且存在移动设备能耗约束的情况下,实现最优的任务缓存和卸载,最小化系统时延。为此主要解决两个问题,即哪些任务需要缓存在边缘云上,以及多少比例的任务需要卸载到边缘云上执行。本文的系统模型如图 1所示。
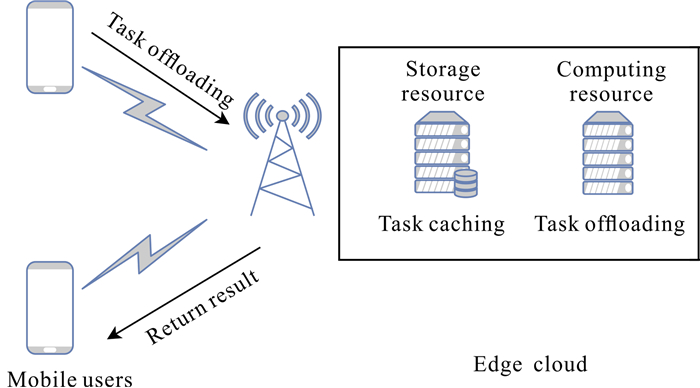
|
| 图 1 多设备系统模型 Fig. 1 Multi-equipment system model |
1.1 场景描述
如图 1所示,本文的MEC场景由多个移动设备和一个MEC边缘云组成。假设移动设备(用户)数量为N={1, 2, …, n},计算任务数量为I={1, 2, …, i},用户发出任务请求后,移动设备可通过无线信道与其边缘云连接。对于移动设备的任务Un, i,用二元组对其定义,即Un, i={Ci, di},其中Ci是完成任务i所需要的计算资源数,也就是CPU周期总数;di是任务i的数据量大小,以bit为单位。
1.2 时延模型不同的设备运行任务会导致时延有所不同。本文考虑两种情况,即当前任务在本地执行的情况以及卸载至边缘云的情况。这两种情况涉及的时延有本地计算时延、移动设备上传数据时延、MEC服务器计算时延、反馈时延。因为反馈时延远小于上传时延,故可忽略不计。
① 本地计算时延。
本地计算时延Tilocal可用下式计算:
| $ T_i^{ {local }}=\frac{C_i}{f_n^{ {local }}}=\frac{d_i \times f_i}{f_n^{ {local }}}, $ | (1) |
其中,fnlocal为移动设备n的本地CPU的计算能力,fi为处理每bit数据量需要的时钟周期数。
② 传输时延。
在计算移动设备上传数据所耗费的时延之前,需要先计算出上传速率Rn。根据香农公式可得:
| $R_n=B \times \log _2\left(1+\frac{P_n \times H_n}{\sigma^2}\right), $ | (2) |
其中,B为移动设备与边缘云之间的无线信道带宽,Pn为移动设备n的发射功率,Hn为无线信道增益,σ2为噪声功率消耗。
由此可得传输时延Titrans为
| $ T_i^{ {trans }}=\frac{d_i}{R_n} \text { 。} $ | (3) |
③ MEC计算时延。
MEC计算时延Tis可用下式计算:
| $ T_i^s=\frac{C_i}{f^s}=\frac{d_i \times f_i}{f^s}, $ | (4) |
其中,fs为MEC服务器的CPU计算能力。
综上可知,将任务卸载到MEC服务器执行的总延迟Tie为
| $T_i^e=T_i^{ {trans }}+T_i^s。$ | (5) |
① 本地计算能耗。
CPU的计算能力与其固有的芯片架构有着密切关系[9],单个CPU计算周期的能耗可表示为ε=κu×f2,κu指的是能量因子,取决于CPU芯片工艺[14],故在本地执行任务的能耗Eilocal为
| $ E_i^{ {local }}=\kappa_u \times\left(f_n^{ {local }}\right)^2 \times C_i。$ | (6) |
② 传输能耗。
移动设备上传数据到边缘云所消耗的能量Enitrans如下:
| $ E_{n, i}^{ {trans }}=P_n \times T_i^{ {trans }}。$ | (7) |
对于任务缓存问题,可定义一个决策变量X1i∈{0, 1}。当X1i=1时,表示任务i缓存到边缘云执行;该值为0则表示不缓存,且任务缓存至边缘云这种情况只需要考虑边缘云执行任务的时延。此处存在边缘云缓存资源约束,即缓存的任务数据总量需小于边缘云的缓存大小。对于任务卸载问题,可定义卸载比例为X2i∈[0, 1]。当X2i=0表示在本地执行任务;当X2i=1则表示全部卸载到边缘云执行;X2i∈(0, 1)时表示卸载X2i的部分任务到边缘云执行;剩余1-X2i部分的任务在本地执行。
综上所述,总时延Ti为
| $ \begin{aligned} & T_i=X 1_i \times T_i^s+\left(1-X 1_i\right) \times\left[X 2_i \times T_i^e+\right. \\ & \left.\left(1-X 2_i\right) \times T_i^{ {local }}\right]=X 1_i \times \frac{C_i}{f^s}+\left(1-X 1_i\right) \times \\ & {\left[X 2_i \times\left(\frac{d_i}{R_n}+\frac{C_i}{f^s}\right)+\left(1-X 2_i\right) \times \frac{C_i}{f_n^{ {local }}}\right] 。} \end{aligned} $ | (8) |
移动设备总能耗Ei为
| $ \begin{gathered} E_i=\left(1-X 1_i\right) \times\left[X 2_i \times E_i^{ {local }}+\left(1-X 2_i\right) \times\right. \\ \left.E_{n, i}^{ {trans }}\right]=\left(1-X 1_i\right) \times\left[X 2_i \times \kappa_u \times\left(f_n^{ {local }}\right)^2 \times C_i+\right.\\ \left.\left(1-X 2_i\right) \times \frac{P_n \times d_i}{R_n}\right]。\end{gathered} $ | (9) |
本算法的优化目标是在边缘云资源与移动设备最大能耗约束的限制下,找到系统时延最小的卸载比例以及缓存决策,因此优化问题可以形式化为
| $\begin{aligned} & \min _{X 1, X 2} \sum\limits_{n=1}^N \sum\limits_{i=1}^I\left\{X 1_i \times \frac{C_i}{f^s}+\left(1-X 1_i\right) \times\left[X 2_i \times\right.\right. \\ &\left(\frac{d_i}{R_n}+\frac{C_i}{f^s}\right)\left.\left.+\left(1-X 2_i\right) \times \frac{C_i}{f_n^{ {local }}}\right]\right\}, \\ & { s.t. } \quad C 1: \sum\limits_{i=1}^I X 1_i d_i \leqslant E_c \\ & C 2: X 1_i \in\{0, 1\}, \forall i \in I \\ & C 3: X 2_i \in[0, 1], \forall i \in I \\ & C 4: E_i \leqslant E_{\max }, \forall i \in I, \end{aligned} $ | (10) |
其中,Ec表示边缘云缓存容量,Emax表示最大能耗约束,约束C1表明缓存任务的数据总量不能大于边缘云的缓存能力;约束C2表明任务缓存决策变量为二进制变量,1与0分别代表缓存与否;约束C3表明可分割部分任务在本地执行,而其余部分在边缘云上执行;约束C4表明移动设备能耗需不超过最大能耗约束。显然,目标函数表示通过任务缓存与对卸载比例的决策,使得系统时延代价最小化。
2 卸载策略基于式(10)的优化目标,本文提出带有缓存机制的GA-PSO卸载策略。该策略将遗传算法和PSO算法融合起来,以便求取边缘计算卸载中的最优卸载比例和缓存决策。策略的核心思想与PSO算法一致,即将待优化问题的搜索空间类比为鸟类的飞行空间,将每一只鸟抽象为一个粒子,每个粒子表征问题的一个可行解,优化问题所要搜索到的最优解等同于鸟类寻找的食物源。其中每个粒子的特征都由适应度、位置和速度来表示,而适应度的好坏决定了粒子的优劣[9]。
基于本文策略实现的算法是在PSO算法的基础上引进生物学的进化思想,加入遗传、突变、自然选择以及杂交等操作,利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,在状态空间中对每一个粒子的位置进行搜索评估,得到局部最优位置(本文中的粒子位置代表卸载比例和缓存决策);然后再从该位置进行搜索,重复以上过程直到得到全局最优位置。此时,适应度也达到收敛状态,该适应度值即为系统时延代价。因为遗传算法收敛速度慢但全局搜索能力强,PSO算法局部搜索能力强但容易陷入早熟,故两者的融合恰好可以弥补彼此的缺陷与局限性。
本文策略算法的设计思路如下:先对粒子进行编码,粒子元素值代表卸载比例与缓存决策;接下来设置需要优化的目标为适应度函数,由于本文主要是针对时延敏感型的任务,所以选取的是系统总时延为适应度值,而总时延的求解公式已在上一节的式(8)中给出。该策略算法实现时,通过进化迭代直至适应度值收敛,从而获得其全局最优解。算法使用罚函数将有约束最优化问题转化为求解无约束最优化问题,在不满足线性约束时让适应度函数值无穷大即可,并采用双循环变量法对最优卸载比例与缓存决策进行求解,再根据适应度函数计算出系统时延代价。下面介绍算法的具体实现。
2.1 粒子编码粒子个体采用浮点数编码,每一个粒子元素可以取0到1.000 1之间的任意浮点数,粒子编码维度与任务总数相同。如若粒子元素值pop=1.000 1时,表明任务缓存到边缘云,而pop∈[0, 1]则表示该值为卸载比例。粒子的速度表示任务部分卸载到边缘云趋势的快慢,记作V={v1, v2, …, vi},粒子速度初始化为-0.1到0.1的随机浮点数,粒子速度编码的维度也应该与任务总数相同。每一个粒子在进化迭代过程中最优位置为Gbest,而所有粒子中出现的最优位置为Zbest,是使得系统代价最小的分配方式。
2.2 适应度函数粒子适应度函数设置为待优化的目标值。由于本文主要是针对时延敏感型任务,优化的对象是该卸载决策与缓存决策时系统的时延总代价,故适应度函数设置如下:
| $\begin{aligned} & \text { Fitness }(p o p)=\sum\limits_{n=1}^N \sum\limits_{i=1}^I T_i=\sum\limits_{n=1}^N \sum\limits_{i=1}^I\left\{X 1_i \times \frac{C_i}{f^s}+\right. \\ & \left(1-X 1_i\right) \times\left[X 2_i \times\left(\frac{d_i}{R_n}+\frac{C_i}{f^s}\right)+\left(1-X 2_i\right) \times\right. \\ & \left.\left.\frac{C_i}{f_n^{ {local }}}\right]\right\}, \end{aligned} $ | (11) |
其中,函数包含了需要求解的两个变量,X1即缓存决策,X2即卸载决策。
2.3 算法流程基于GA-PSO和缓存机制的卸载策略的算法可以描述为以下7个步骤。
步骤1:设置交叉概率、变异概率、学习因子、惯性权重、最大迭代次数、粒子群规模数、粒子的最大速度、位置边界等算法控制参数,在速度区间和搜索空间上随机初始化粒子的速度和位置;
步骤2:定义适应度函数,根据初始值计算公式(8)所求的时延,再通过公式(11)的累加计算出初始适应度值;
步骤3:循环开始,根据所求出的粒子位置计算出个体极值与全局极值。个体极值为每个粒子找到的最优解,再从这些最优解可找到全局最优解;
步骤4:使用粒子群公式更新每个粒子的位置与速度,并依据交叉、变异概率进行相应的染色体操作,得到新的种群;
步骤5:如若新种群符合约束条件就求更新后的适应度值,不符合约束条件则将适应度值设为无穷大,使其自然淘汰;
步骤6:将全局最优方案代入公式(8),累加后计算出新的适应度值。如果新求出的适应度值比历史值小,则返回步骤3并更新个体和全局最优分配方案;
步骤7:判断循环结束的条件是目标函数的适应度达到期望值或者进化到预先设定的代数,算法结束的判定是进化到预先设定的代数即可终止,算法结束时输出全局最优解与适应度值,前者表示最优卸载比例与缓存决策,后者则表示该方案下的时延。
该算法的伪代码如下。
输入:
① 本地任务集合:I={1, 2, …, i};
② 算法控制参数:粒子群规模par_num=100,迭代次数maxgen=100,位置边界popmin与popmax分别为粒子编码的最小值与最大值,学习因子c1=c2=1.5,惯性权重w=0.5,交叉概率pc=0.7,变异概率pm=0.3。
输出:最优卸载比例与缓存决策,以及最小时延
算法的主要过程:
① 初始化: popsize, maxgen, popmin, popmax, c1, c2, w, oc, pm, V, pop
② for i =1 to maxgen do
③ for j =1 to popsize do
④ V(j, :)=V(j, :)+c1*rand*(gbest(j, :)-pop(j, :))+c2*rand*(zbest- pop(j, :));
⑤ pop(j, :)=pop(j, :)+w*V(j, :);
⑥ repeat
⑦ mpick, cpick ← rand
⑧ if mpick>pm then
⑨ Randomly select where to mutate
⑩ Mutation operation
⑪ end if
⑫ if cpick > pc then
⑬ Randomly select where to cross
⑭ Cross operation
⑮ end if
⑯ until Both chromosomes are available after mutating and crossing
⑰ if The constraints of cache and power consumption are not met then
⑱ Fitness(pop) ← Inf
⑲ else
⑳ Update Fitness(pop) based on Equation(11)
㉑ if Fitnessgbest, Fitnesszbest>Fitness(pop) then
㉒ Update Fitnessgbest, Fitnesszbest, Gbest, Zbest
㉓ end if
㉔ end if
㉕ end for
㉖ end for
3 仿真实验与结果分析 3.1 仿真环境及参数设置仿真实验环境是通过Matlab语言构造一个由边缘云和移动设备组成的边缘计算系统,在该实验系统上实现本文提出的基于GA-PSO和缓存机制的卸载策略,并具体评估了该策略的性能。假设移动设备与边缘云之间的无线信道带宽B=1 GHz,移动设备的发射功率Pn=0.5 W,对应的噪声功耗σ2=1×10-9,无线信道增益Hn=2×10-10-2×10-6。任务i的数据量大小di=7-40 Mbit,处理每bit数据量需要的时钟周期数fi=800-1 000 cycles/bit,移动设备n的本地CPU周期频率fnlocal=2-4 GHz,MEC服务器的CPU周期频率fs=5-8 GHz,边缘云缓存大小Ec =500 Mbit,移动设备的CPU固有系数κu=5×10-27。
3.2 实验结果与性能分析本文实验的目的有二:一是验证本算法的有效性和收敛性,二是通过一些仿真实验从多角度比较和评估在不同参数下本文提出的卸载策略的性能。实验中,假设本地设备也可处理高计算量的任务,且任务到达即可执行,不考虑任务排队导致的时延增长。
首先对本文的GA-PSO卸载策略的收敛性进行评估,设置设备数I=100,其余参数设置如3.1节所示。图 2给出了GA-PSO卸载策略收敛性的实验结果。从图 2可以观察到,本算法在前25次进化迭代过程中收敛速度较快,而后其适应度值保持不变,说明已找到全局最优解。
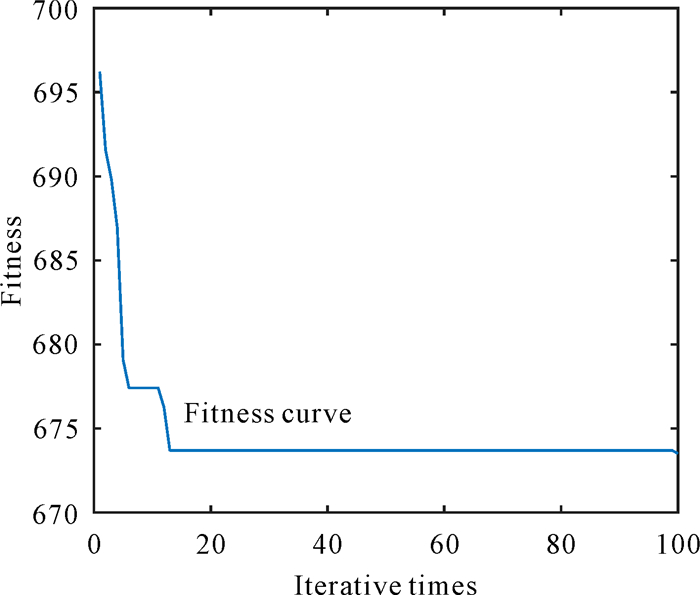
|
| 图 2 收敛性分析图 Fig. 2 Graph of convergence analysis |
接着比较本文带缓存机制的GA-PSO卸载算法、不带缓存机制的GA-PSO卸载算法、本地计算和将所有任务卸载到MEC服务器这4种方案的系统时延,实验对比结果如图 3所示。从图 3可以看出,当设备数为25,50,75,100,125时,这4种策略的系统总延迟均随着设备数增长呈增加趋势,而本文策略的系统时延小于其他3种方案的时延。由于设备数越多,任务量也会随之增加,从而导致时延上升。但是,本文策略加入了缓存机制并使用改进的算法,使得缓存的任务只需要考虑边缘云执行任务的时延,不存在上传时延,所以耗费时间比需要卸载的非缓存任务的执行时间短,从而使得系统时延达到最小化。

|
| 图 3 设备数对系统时延的影响 Fig. 3 Impact of device number on system delay |
第3个实验是测试分析边缘云缓存容量与设备能耗、时延之间的关系,实验的目的是分析缓存与否以及缓存容量的大小对设备总能耗与系统时延产生的影响。图 4给出了使用本文的GA-PSO卸载策略、本地计算和将所有任务卸载到MEC服务器这3种方案后边缘云缓存容量与系统能耗、时延之间的关系。图 4使用了双坐标轴图,左边的纵坐标是系统能耗,右边的纵坐标为时延。从图 4可以看出,随着缓存资源的增加,能耗有降低的趋势,也就是边缘云可以缓存的任务数据越多,移动设备的耗能就越低;此外,本地计算的能耗明显比本文的GA-PSO卸载策略的能耗高,表明本文卸载策略在一定程度上降低了移动设备的能耗。这是因为部分任务的相关数据已经缓存到边缘云,执行此类任务移动设备不产生能量消耗。从图 4还可以看出,边缘云缓存容量越大,系统时延就越小,说明缓存对时延有较大影响。这是因为缓存容量越大,可缓存任务的数量越多,而缓存任务的执行时间比需要卸载的非缓存任务的执行时间短。
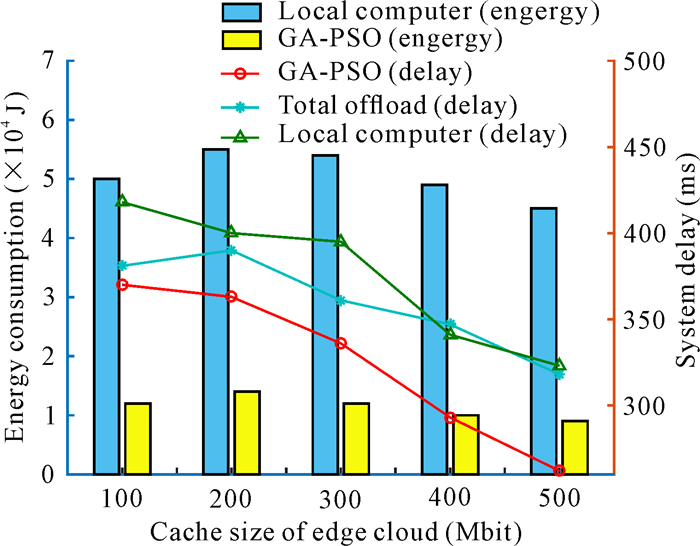
|
| 图 4 边缘云缓存能力对系统时延及能耗的影响 Fig. 4 Impact of edge cloud caching capability on system delay and energy consumption |
4 结束语
本文提出了一个基于GA-PSO和缓存机制的卸载策略,该策略兼具遗传算法的全局搜索优势与PSO算法的局部搜索优势,搜索速度快,可以得到最优的卸载比例与缓存决策。仿真实验结果分析表明,与本地计算、全部卸载以及无缓存的卸载策略相比,本文的GA-PSO卸载策略使得本地设备与边缘云协作计算,可以降低移动边缘计算的时延代价。未来还可将PSO算法与其他优化算法结合,寻求一个可靠性更高的卸载策略。
| [1] |
郭煜. 移动边缘计算中带有缓存机制的任务卸载策略[J]. 计算机应用与软件, 2019, 36(6): 114-119. |
| [2] |
谢人超, 廉晓飞, 贾庆民. 移动边缘计算卸载技术综述[J]. 通信学报, 2018, 39(11): 138-155. |
| [3] |
CHEN X, JIAO L, LI W Z, et al. Efficient multi-user computation offloading for mobile-edge cloud computing[J]. IEEE/ACM Transactions on Networking, 2015, 24(5): 2795-2808. |
| [4] |
MIN C, HAO Y X, QIU M K, et al. Mobility-aware caching and computation offloading in 5G ultra-dense cellular net-works[J]. Sensors, 2016, 16(7): 974. DOI:10.3390/s16070974 |
| [5] |
WEI Q Y, LIU L A, WEI F S, et al. Computational offloading strategy based on dynamic particle swarm for multi-user mobile edge computing[C]// 2019 IEEE Symposium Series on Computational Intelligence (SSCI). Xiamen, China: IEEE, 2019: 2890-2896.
|
| [6] |
BI J, YUAN H T, DUANMU S, et al. Energy-optimized partial computation offloading in mobile-edge computing with genetic simulated-annealing-based particle swarm optimization[J]. IEEE Internet of Things Journal, 2021, 8(5): 3774-3785. DOI:10.1109/JIOT.2020.3024223 |
| [7] |
LI S, GE H B, CHEN X T, et al. Computation offloading strategy for improved particle swarm optimization in mobile edge computing[C]//2021 IEEE 6th International Conference on Cloud Computing and Big Data Analytics (ICCCBDA). Chengdu, China: IEEE Press, 2021: 375-381.
|
| [8] |
AL-HABOB A A, DOBRE O A, ARMADA A G, et al. Task scheduling for mobile edge computing using genetic algorithm and conflict graphs[J]. IEEE Transactions on Vehicular Technology, 2020, 69(8): 8805-8819. DOI:10.1109/TVT.2020.2995146 |
| [9] |
罗斌, 于波. 移动边缘计算中基于粒子群优化的计算卸载策略[J]. 计算机应用, 2020, 40(8): 2293-2298. |
| [10] |
缪裕青, 徐伊, 张万桢, 等. 车联网中改进粒子群算法的任务卸载策略[J]. 计算机应用研究, 2021, 38(7): 2050-2055. |
| [11] |
刘炎培, 陈宁宁, 朱运静, 等. 面向5G/Beyond 5G的移动边缘缓存优化技术综述[J]. 计算机应用, 2022, 42(8): 2487-2500. |
| [12] |
NATH S, WU J X. Deep reinforcement learning for dynamic computation offloading and resource allocation in cache-assisted mobile edge computing systems[J]. Intelligent and Converged Networks, 2020, 1(2): 181-198. |
| [13] |
LAN Y W, WANG X X, WANG D Y, et al. Task caching offloading and resource allocation in D2D-aided fog computing networks[J]. IEEE Access, 2019, 7: 104876-104891. |
| [14] |
LI M L, ZHOU X B, QIU T, et al. Multi-relay assisted computation offloading for multi-access edge computing systems with energy harvesting[J]. IEEE Transactions on Vehicular Technology, 2021, 70(10): 10941-10956. |



