2. 同济大学测绘与地理信息学院,上海 200092
2. College of Surveying and Geographic Informatics, Tongji University, Shanghai, 200092, China
近年来,国内的大地学者提出将陆地-岛礁-海面基准向海底基准传递,逐步建设健全海底大地基准网[1-4],以期为海洋安全、海洋经济开发、海洋科学研究、海洋环境监测等提供综合定位、导航、授时服务[5]。1985年美国斯克利普斯海洋研究所Spiess教授[6]首次提出采用全球导航卫星/声学定位(Global Navigation Satellite System-Acoustic,GNSS-A)相结合的方式建立海底大地基准,GNSS-A技术是GNSS动态定位和水声测距的一种组合技术,集卫星定位、水声定位和水声通讯于一体,可实现由卫星向水下或海底目标的实时高精度定位[7-9]。21世纪以来,美国、加拿大、日本、俄罗斯等国家基于GNSS-A技术,通过周期性测量和标校实现长期维持高精度的海洋大地测量基准[10-13]。我国的海底大地基准建设起步较晚,但已取得了比较大的突破,2019年7月在水深3 000 m海域进行了海底大地基准网布设及观测实验,通过GNSS-A技术对5个海底基准点开展圆走航加十字型的对称观测,获取了高精度的定位结果[14]。
在水下定位技术中,安装于船底的声学换能器可实时测量与目标之间的传播时间,乘以声速就是两点之间的距离。该种模式结构简单、操作便利,大大提高了海底目标定位的精度和效率[15, 16]。为了提高水下定位精度,国内外研究学者致力于削弱各类误差。Xu等[17]提出了基于对称航迹的水下差分定位技术,使用差分算子削弱系统误差,可以提高GNSS-A技术的定位精度。一些学者将未建模的系统误差设成未知参数或者建模后估计,以消除对定位的影响[18, 19]。Zhao等[20]从随机模型出发,建立了基于声线入射角的水下定位随机模型,实验证明其优于传统的等权随机模型定位结果。邝英才等[21]和Zhao等[22]提出了一种GNSS-A整体解算方法,不同类型观测值纳入统一模型,提升了海底控制点的定位精度和稳定性。这些研究为我国海底控制网的建设打下了理论基础,也为本文提供了参考和借鉴。
基于GNSS-A技术在垂直方向上存在固有的几何缺陷,使得海底大地基阵网垂直方向的定位精度受以声速为主的误差影响明显[23]。此外,受涌浪影响,船体姿态对水面GNSS定位精度的影响可由运动传感器实时改正,水下测距的精度主要受声速误差和噪声的影响。水平观测结构对称的测线可以减弱系统误差对观测精度的影响,同时抵消部分粗差,从而提高海底目标在水平方向的精度[24, 25];利用实测声速剖面开展声线跟踪可以进一步削弱声速误差的影响,最终提高海底目标的定位精度[26, 27]。
本文基于GNSS-A绝对标校技术,研究提高海底目标垂直定位精度的解算方案。针对双程传播时延问题,给出一种基于动态观测的海底目标定位算法;针对声学测距易受声速误差影响的特性,结合实测声速剖面开展声线跟踪并构造迭代。通过现场实验,验证本文所提出的海底目标定位算法的精度与可靠性。
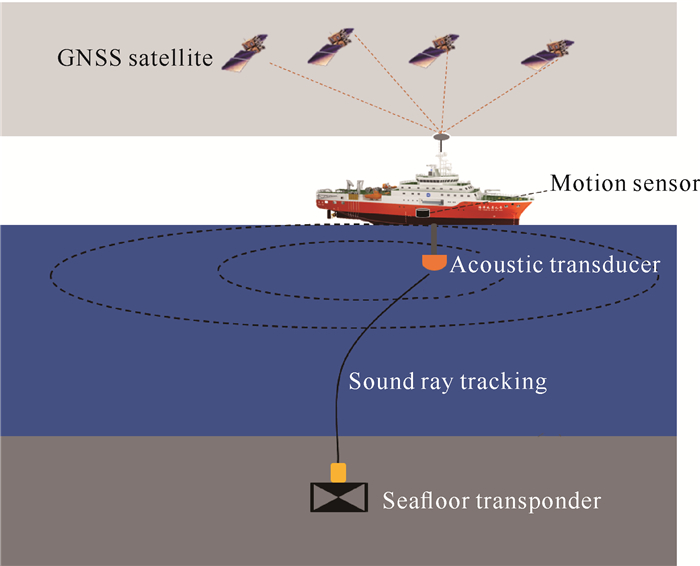
1 GNSS-A海底目标定位原理 1.1 GNSS-A技术原理GNSS-A技术是综合利用GNSS、声波传播时间和声速剖面测量等方法计算海底目标的位置,主要分为两个部分:一是通过建立严密的站心地平坐标系,确定声学换能器在大地坐标系下的实时位置;二是通过声线追踪并构造迭代计算声学换能器与海底应答器之间的距离[28]。如图 1所示,测量船上安装有GNSS接收机(可接收GNSS卫星信号)、运动传感器和安装于船底的声学换能器。测量船绕海底应答器航行时,声学换能器向海底发射声学信号,换能器接收到海底应答器的反馈信号并记录声波的传播时间,结合实测的声速剖面数据,计算声学换能器与海底应答器之间的距离[29, 30]。GNSS接收机可实时获取测量船的位置信息,运动传感器可同步测量船体姿态信息。在船体坐标系中,GNSS天线与传感器之间的位置关系在安装前经过精确标定以及运动姿态传感器数据的补偿就可确定声学换能器的位置。
|
| 图 1 GNSS-A海底目标定位原理示意图 Fig. 1 Diagram of GNSS-A seafloor target positioning principle |
1.2 声学换能器实时动态定位
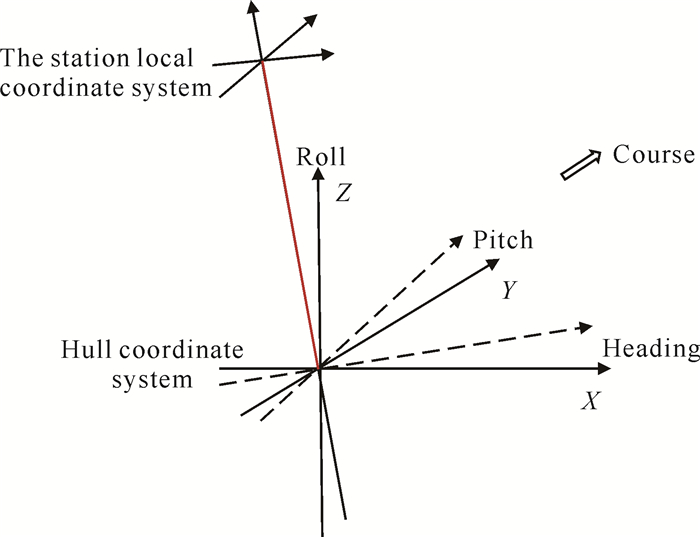
GNSS接收机可实时获取测量船的位置,确定船底换能器和GNSS接收机的相对位置关系,通过坐标改正就可以计算声学换能器的位置。由于GNSS接收机得到的是天线相位中心在WGS-84坐标系下的坐标,需将GNSS的坐标改化到声学换能器中心。船体坐标系与以GNSS接收机相位中心为原点的站心地平坐标系的位置关系如图 2(红线代表GNSS天线相位中心与船体坐标系中心的连线)所示[31]。
|
| 图 2 船体坐标系与站心地平坐标系位置关系示意图 Fig. 2 Diagram of position relation between hull coordinate system and station local coordinate system |
计算声学换能器在以GNSS接收机相位中心为原点的站心地平坐标系的坐标改正数的计算方法如公式(1)所示。
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \left(\begin{array}{l} \triangle X \\ \triangle Y \\ \triangle Z \end{array}\right)_{\text {站心地平坐标系 }}=H_{\text {heading }} \cdot H_{\text {pitch }} \cdot H_{\text {roll }} \cdot\\ \left(\begin{array}{l} x \\ y \\ z \end{array}\right)_{船体坐标系}, \end{array} $ | (1) |
其中,Hheading、Hpitch、Hroll分别为
| $ \begin{aligned} &\ \ \ \ \ \ \ \ \ \ H_{\text {heading}}=\\ &\left(\begin{array}{ccc} \cos (\text {heading}) & -\sin (\text {heading}) & 0 \\ \sin (\text {heading}) & \cos (\text {heading}) & 0 \\ 0 & 0 & 1 \end{array}\right), \end{aligned} $ | (2) |
| $ \begin{aligned} &\ \ \ \ \ \ \ \ \ \ H_{\text {pitch}}=\\ &\left(\begin{array}{ccc} \cos (\text {pitch}) & 0 & -\sin (\text {pitch}) \\ 0 & 1 & 0 \\ \sin (\text {pitch}) & 0 & \cos (\text {pitch}) \end{array}\right), \end{aligned} $ | (3) |
| $ \begin{aligned} &\ \ \ \ \ \ \ \ \ \ H_{\text {roll}}= \\ &\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos (\text {roll}) & -\sin (\text {roll}) \\ 0 & \sin (\text {roll}) & \cos (\text {roll}) \end{array}\right), \end{aligned} $ | (4) |
式中,heading为偏航角,船右舷为正、左舷为负;pitch为纵摇角,船头向上为正、向下为负;roll为横摇角,船右舷为正、左舷为负;(x y z)船体坐标系T是GNSS接收机与声学换能器在船体坐标系下的基线向量。
2 GNSS-A海底目标定位算法 2.1 基于动态观测的海底目标定位算法基于海面浮标方式的海底声学定位,其声学换能器在一次测量的发射与接收过程中,因浮标的移动速度通常较小,一次测量中双程传播时延造成的位置变动可忽略,因此可将发射与接收当作单次观测;而在船载走航动态观测中,忽略双程传播时延,则会引入新的误差,即测量船在换能器发射信号到接收信号时处在不同位置,本文针对这种影响,将声学换能器动态观测中的发射与接收信号的过程分别考虑[32]。
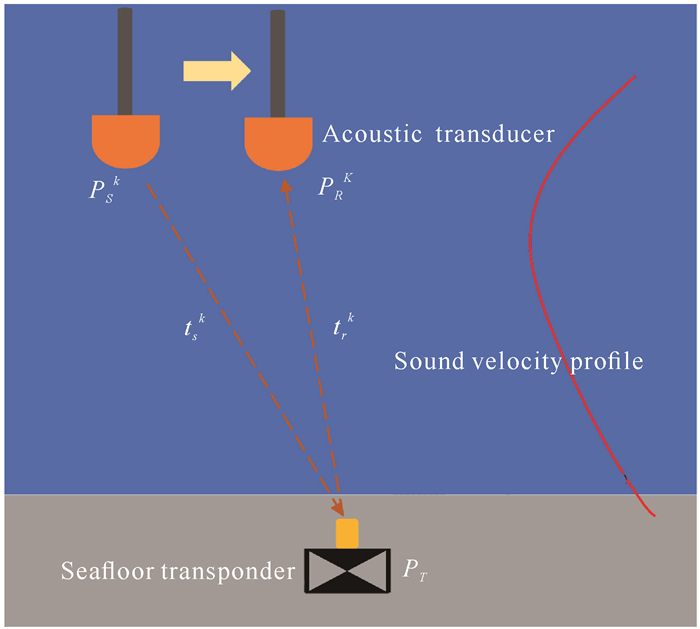
如图 3所示,海底应答器坐标为PT,设在第k次观测中,声学换能器向海底应答器发射信号时位置为PSk,海底应答器接收到声信号并作出响应,此时声学换能器至海底应答器的距离为ρSk,声学换能器接收到海底应答器返回信号时的位置为PRk,此时海底应答器至声学换能器的距离为ρRk,则观测方程为
| $ \rho_S^k+\rho_R^k=f\left(P_S^k, P_T^k\right)+f\left(P_R^k, P_T^k\right)+\varepsilon_u^k+\varepsilon^k, $ | (5) |
| $ \begin{array}{l} \ \ \ \ \ \ \ \ f\left(P_S^k, P_T^k\right)= \\ \sqrt{\left(x_t^k-x_s^k\right)^2+\left(y_t^k-y_s^k\right)^2+\left(z_t^k-z_s^k\right)^2}, \end{array} $ | (6) |
| $ \begin{array}{l} \ \ \ \ \ \ \ \ f\left(P_R^k, P_T^k\right)= \\ \sqrt{\left(x_t^k-x_r^k\right)^2+\left(y_t^k-y_r^k\right)^2+\left(z_t^k-z_r^k\right)^2}, \end{array} $ | (7) |
|
| 图 3 动态定位示意图 Fig. 3 Dynamic positioning diagram |
式中,f(PSk, PTk),f(PRk, PTk)分别为换能器在发射和接收信号时与海底应答器的距离,εuk为与声学换能器的测距误差,εk为其他噪声引起的测距随机误差[33]。
利用声速剖面仪实时获取的声速剖面结合公式(8)计算Harmonic平均声速:
| $ C_H=\left(z-z_0\right)\left[\int_{z_0}^z \frac{\mathrm{d} z}{C(z)}\right]^{-1}。$ | (8) |
根据泰勒级数公式在PT0处展开,式(5)可线性化为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \rho_{S_0}^k+\rho_{R_0}^k-f_S^0-f_R^0=a_s^k \mathrm{~d} X+a_r^k \mathrm{~d} X+\varepsilon_u^k+\\ \varepsilon^k, \end{array} $ | (9) |
式中,ρkS0和ρkR0分别代表声学换能器发射和接收声信号时至海底应答器的欧式距离,且
| $ \left\{\begin{array}{l} \rho_{S_0}^k=C_H \cdot t_s^k \\ \rho_{R_0}^k=C_H \cdot t_r^k \end{array}, \right. $ | (10) |
式中,CH为平均声速,tsk和trk分别为换能器至应答器和应答器至换能器的单程传播时间。ask和ark为雅各比矩阵,系数为
| $ \left\{\begin{array}{l} a_s^k=\left[\begin{array}{lll} \frac{\partial f_s^k}{\partial x_0} & \frac{\partial f_s^k}{\partial y_0} & \frac{\partial f_s^k}{\partial z_0} \end{array}\right] \\ a_r^k=\left[\begin{array}{lll} \frac{\partial f_r^k}{\partial x_0} & \frac{\partial f_r^k}{\partial y_0} & \frac{\partial f_r^k}{\partial z_0} \end{array}\right] \end{array}\right., $ | (11) |
| $ \begin{aligned} &\left\{\begin{array}{c} \frac{\partial f_i^k}{\partial x_0}=\frac{x_{t_0}^k-x_i^k}{f_i^0} \\ \frac{\partial f_i^k}{\partial y_0}=\frac{y_{t_0}^k-y_i^k}{f_i^0} \\ \frac{\partial f_i^k}{\partial z_0}=\frac{z_{t_0}^k-z_i^k}{f_i^0} \\ f_i^0=\sqrt{\left(x_{t_0}^k-x_i^k\right)^2+\left(y_{t_0}^k-y_i^k\right)^2+\left(z_{t_0}^k-z_i^k\right)^2} \end{array}\right., \\ &i=s, r, \end{aligned} $ | (12) |
式中,(xkt0, ykt0, zkt0)为海底应答器的初始坐标值。根据式(9)得距离的残差v: v=εuk+εk,利用最小二乘vTv=min解算海底应答器的位置。
2.2 基于声线跟踪的距离迭代算法水平对称结构的观测可削弱系统误差在水平方向的影响,对于改善水平方向的定位精度具有较好的效果。但在垂直方向上,由于声速误差等系统误差的影响,精度改善并不明显[34, 35]。为了研究该问题,本文给出基于实测声速剖面的距离迭代计算方法,通过提高声学测距精度,改善海底应答器垂直方向定位精度。
首先根据水深、换能器吃水深度和实测的声速剖面将换能器至应答器的距离划分为n层,利用计算得到的目标初始深度和测量船与海底应答器的平距计算初始入射角θ,基于层内常梯度声线跟踪方法计算水平、垂向分量和传播时间[36, 37]:
| $ \left\{\begin{array}{l} y_T=\sum\limits_{i=1}^n y_i, z_T=\sum\limits_{i=1}^n z_i \\ y_i=\frac{\sqrt{1-\left(p c_i\right)^2}-\sqrt{1-p^2\left(c_i+g_i \Delta z_i\right)^2}}{p g_i} \\ t_i=\frac{1}{\left|g_i\right|} \ln \left[\frac{c_i+g_i \Delta z_i}{c_i} \frac{1+\sqrt{1-\left(p c_i\right)^2}}{1+\sqrt{1-p^2\left(c_i+g_i \Delta z_i\right)^2}}\right] \end{array}\right., $ | (13) |
式中,yi和ti分别为经历水层厚度Δzi的水平位移量和传播时间,p为snell常数;ci、θi分别为波束经历第i层上界面的声速和入射角,ci+1、θi+1分别为波束经历第i层下界面的声速和入射角,声速在层内以常梯度gi=(ci+1-ci)/(zi+1-zi)变化,入射角可以根据以下公式计算:
| $ \theta=-\arctan \left(y_T / z_T\right) 。$ | (14) |
利用解算后的坐标根据(14)式重新计算入射角,再结合观测时间开展声线跟踪更新应答器的坐标。重复上述过程,直到相邻两次确定的坐标小于给定的限差ε。
| $ \left\{\begin{array}{l} y_T^{i+1}-y_T^i \leqslant \varepsilon_y \\ \left|z_T^{i+1}-z_T^i\right| \leqslant \varepsilon_z \end{array}\right., $ | (15) |
式中,(y, z)Ti和(y, z)Ti+1分别为第i次和第i+1次信标点的定位结果,εy和εz为迭代终止坐标阈值。
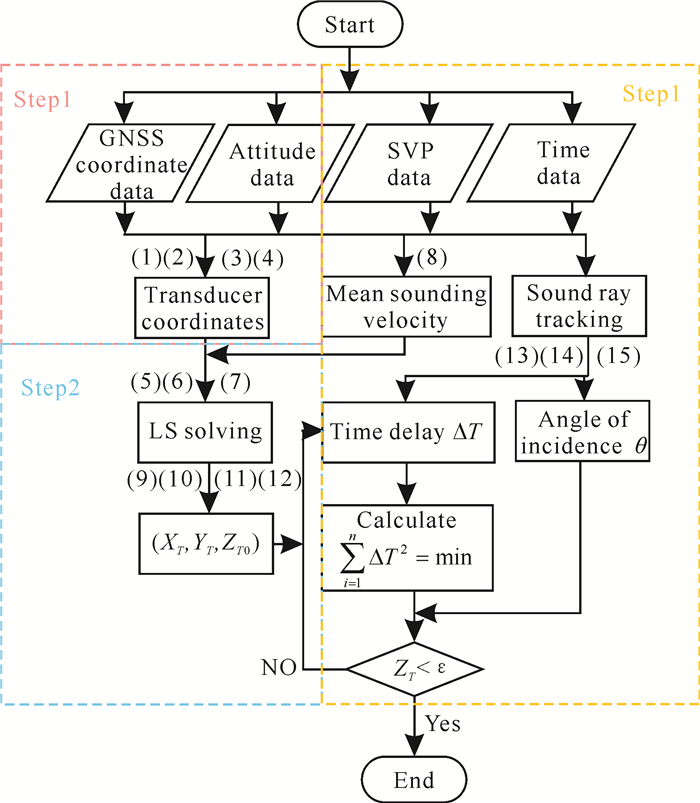
本文提出的基于GNSS-A的海底目标定位算法如图 4所示,过程大致分3步。
|
| 图 4 GNSS-A海底目标定位算法流程图 Fig. 4 Flow chart of GNSS-A seafloor target positioning algorithm |
第一步:根据GNSS接收机和声学换能器基阵之间的向量关系与实时获取的姿态数据,结合式(1)计算声学换能器在以GNSS接收机相位中心为原点的站心地平坐标系下的坐标改正数,进而求得声学换能器的实时位置PS(XS, YS, ZS)和PR(XR, YR, ZR)。
第二步:根据声学换能器测得的与海底应答器的传播时间tS和tR,结合声速剖面计算的平均声速CH,计算声学换能器与海底应答器之间的距离ρS和ρR;采用换能器的平面坐标平均值作为海底应答器的平面坐标初始值(XT0, YT0)、水深和换能器吃水深度的差值作为海底应答器初始垂直坐标ZT0,采用最小二乘(Least Squares, LS)法并结合式(9)进行平差,计算海底应答器的坐标改正数(Δx, Δy, Δz)和残差向量V1,得到平面坐标较准确的海底应答器坐标(XT, YT, ZT1)。
第三步:根据解算得到的海底应答器坐标(XT, YT, ZT1)和声速剖面数据开展声线跟踪,利用式(14)、式(15)迭代出更为准确的传播时间t和入射角θ,计算观测时间tS和tR与传播时间t的时间延迟ΔT,并依据
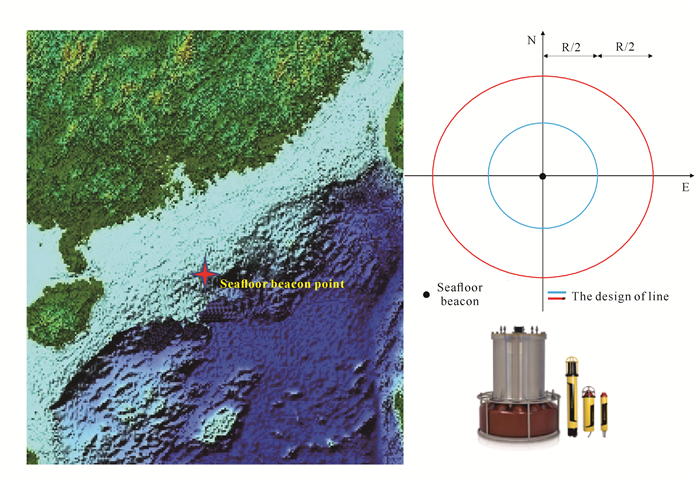
为验证本文定位算法的精度和可靠性,海洋地质九号船于2021年4月3日在中国南海进行了GNSS-A海底目标定位实验。实验涉及的仪器有GNSS星站差分定位仪Veripos LD5,水平和垂向定位精度分别为10 cm和20 cm;运动传感器Kongsberg MRU5,角速率动态精度和加速度精度分别为0.02°和0.01 m/s2;超短基线定位系统Kongsberg HiPap 102P,其声学换能器水下测距精度为0.02 m;移动船载声速测量系统AML MVP300,最大测量深度为3 350 m,声速测量精度为0.05 m/s,其搭载的四电极电导率传感器精度为0.001 S/m,精密热敏电阻温度传感器精度为0.005℃,应变片式压力传感器精度为测量水深的0.05%。实验开始前将声学信标绑定到可回收的装置中投入海底,并以此位置为圆心,分别设计两个不同半径的圆形对称实验测线。图 5所示的是实验区域及设计的测线和部分仪器。
|
| 图 5 南海实验区域及设计测线和HiPap 102P声学换能器及信标 Fig. 5 South China Sea test area and design survey line and HiPap 102P′s transducer and transponder |
实验区水深约1 750 m,为确保测量实验的精度和几何结构,设计以约0.6倍水深和1.2倍水深为半径的圆形测线,设计半径分别为1 000 m和2 000 m,可以保证声波入射角在合理范围内。
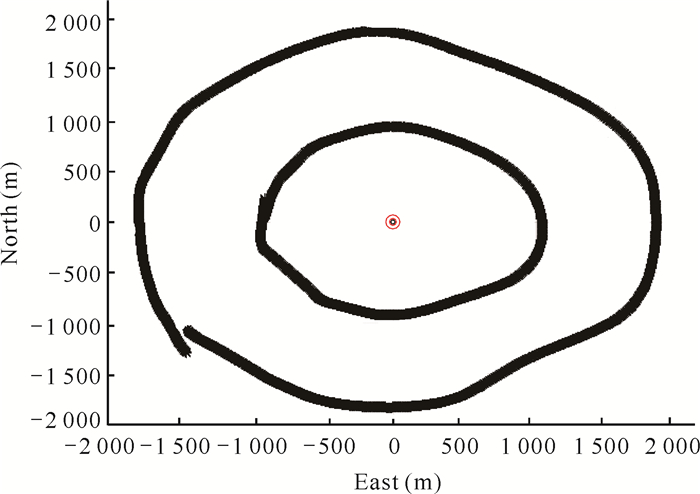
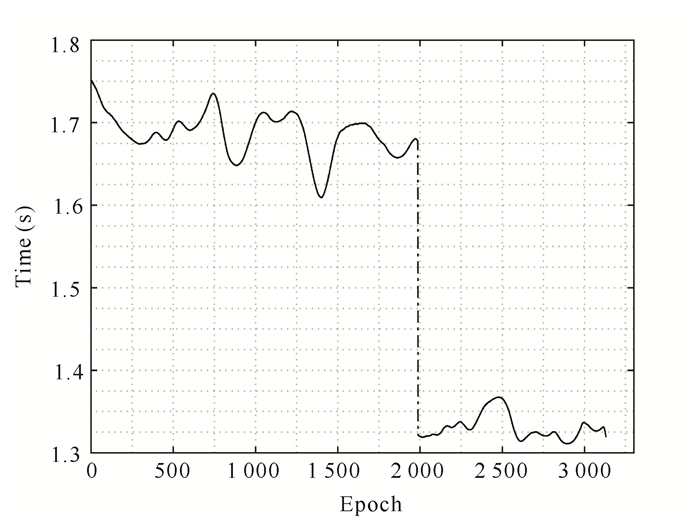
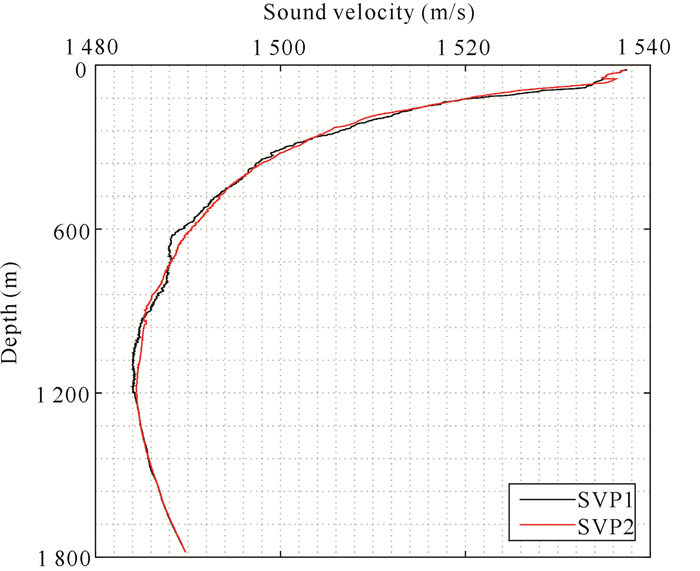
实验期间测量船以4节船速匀速行驶,顺序是测量船先沿大圆测线航行后沿小圆测线航行,图 6中红色圆圈是海底信标的位置,黑色圆圈是测量船在实验期间的实际航迹图,图 7为实验中声学换能器发射声波至海底信标的旅行时间的统计,大圆平均每次测距时间约为1.68 s(单程),小圆平均每次测距时间约为1.33 s(单程)。移动船载声速测量系统获取的实验时间期间两次测量的声速剖面数据如图 8所示,两个声速剖面的平均声速约为1 492 m/s。
|
| 图 6 测量船实际航迹图 Fig. 6 Actual track chart of survey ship |
|
| 图 7 声学换能器观测时间统计 Fig. 7 Statistics of acoustic transducer observation time |
|
| 图 8 两次测量的声速剖面图 Fig. 8 Sound velocity profile of two measurements |
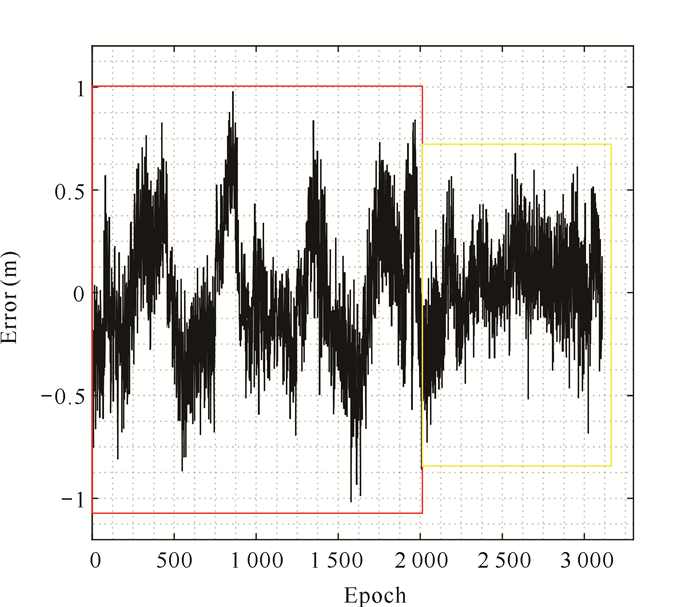
采用观测数据的平均值作为海底信标的初始坐标,结合观测数据代入观测式(9)中解算海底信标的位置,图 9为利用LS法计算的声学换能器与海底信标的距离残差。声学换能器历元间测量是独立同精度观测,因此对残差进行统计,并采用以下单位权中误差对测量结果精度评定[38]:
| $ \sigma=\sqrt{\frac{V^{\mathrm{T}} V}{n-t}}, $ | (16) |
|
| 图 9 LS法解算的海底信标距离残差 Fig. 9 Distance deviation of seafloor beacon calculated by LS method |
式中,V为测量残差向量,t为必要观测的个数,本文t=3。
如图 9所示,红色框内是大圆测线解算的残差,黄色框内是小圆测线解算的残差,残差均匀分布在零轴附近,且小圆的残差小于大圆的残差。残差最大为0.98 m,最小为-1.09 m,在水深1 750 m的情况下,单位权中误差为0.29 m,说明观测结果具有较好的测量精度。对于海底信标的位置解算结果,采用北东天(North East Up,NEU)3个方向坐标分量和相对点位中误差对平差结果精度评定。平差参数中误差是评价观测数据内符合精度的指标,其值越小代表内符合精度越好,采用LS法解算的海底信标点的相对点位中误差为0.91 cm,北方向、东方向和垂直方向的误差分量分别为0.58 cm、0.60 cm和0.35 cm。
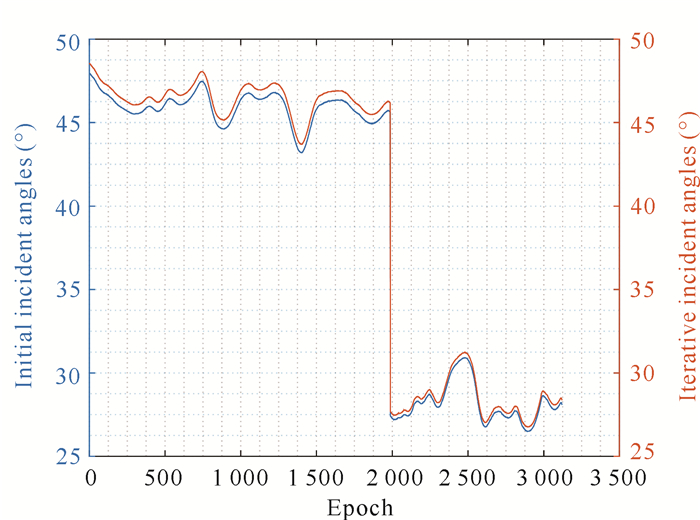
实验中垂直方向上的定位精度主要受声速误差的影响,因垂直方向上观测结构不对称,无法抵消垂直方向上的误差,采用声线跟踪可以减弱声速误差对观测距离的影响,提高海底信标在垂直方向上的定位精度。利用LS法解算的结果结合常梯度声线跟踪进行观测距离的迭代计算,图 10给出了初始入射角和迭代入射角的对比。
|
| 图 10 初始入射角和迭代入射角对比图 Fig. 10 Comparison of initial and iterative incident angles |
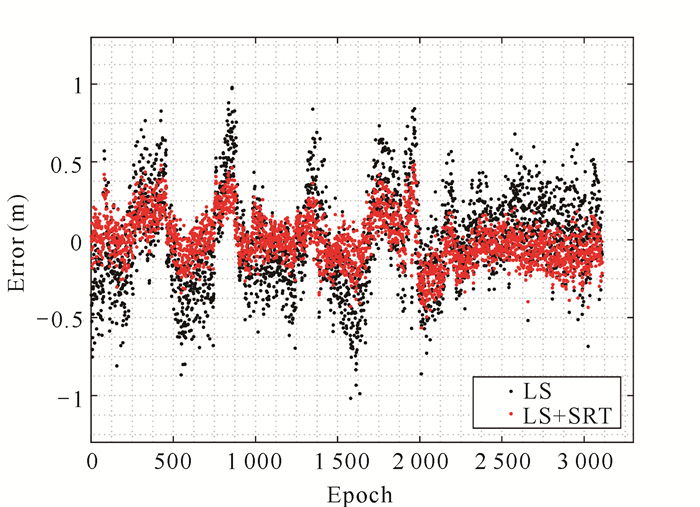
声线跟踪采用初始入射角进行迭代计算,利用迭代后的位置信息更新入射角,直至迭代出更准确的海底信标的位置。通过初始入射角和迭代后入射角的对比可以看出,大圆入射角为43-47°,小圆入射角为26-31°,迭代后入射角均略大于初始入射角,证明声线跟踪有效追踪声线在水中的实际传播路径,提高了观测距离的精度。图 11给出了本文方法和LS法解算观测距离的残差对比结果,表 1统计了两种方法的精度信息。
|
| 图 11 两种方法的距离残差对比图 Fig. 11 Comparison of distance residual between the two methods |
| 方法 Method |
最大残差(m) Max residual(m) |
最小残差(m) Min residual(m) |
单位权中误差σ(m) Unit weight median error σ(m) |
| LS | 0.98 | -1.09 | 0.29 |
| LS+SRT | 0.42 | -0.62 | 0.20 |
从对比结果可以看出,采用本文方法解算结果的残差分布更密集,残差的极值也均小于LS法的解算结果;在观测距离为2 600 m的情况下,单位权中误差从0.29 m减小到了0.20 m,说明本文方法可以有效减弱声速误差对测距精度的影响,提高观测的精度,进而提高海底信标在垂直方向的定位精度。
4 结论针对声速误差对海底目标定位精度的影响,本文研究了GNSS-A海底目标高精度定位的算法,通过南海实测的深海实验数据验证了本文算法的有效性。实验结果表明:基于动态观测的海底目标定位算法能综合利用发射和接收过程中的观测数据,解决双程传播时延引起的位移误差问题,提高了海底目标的水平定位精度,获得了点位中误差优于1 cm的平差结果;基于声线跟踪的距离迭代算法可有效减弱声速误差对测距精度的影响,距离残差的单位权中误差从0.29 m减小到了0.20 m。本文算法可为提高海底目标垂直方向的定位精度提供参考。
| [1] |
刘经南, 陈冠旭, 赵建虎, 等. 海洋时空基准网的进展与趋势[J]. 武汉大学学报(信息科学版), 2019, 44(1): 17-37. |
| [2] |
李林阳, 柴洪洲, 李姗姗, 等. 海洋立体观测网建设与发展综述[J]. 测绘通报, 2021(5): 30-37. DOI:10.13474/j.cnki.11-2246.2021.0137 |
| [3] |
周兴华, 付延光, 许军. 海洋垂直基准研究进展与展望[J]. 测绘学报, 2017, 46(10): 1770-1777. DOI:10.11947/j.AGCS.2017.20170322 |
| [4] |
杨元喜, 徐天河, 薛树强. 我国海洋大地测量基准与海洋导航技术研究进展与展望[J]. 测绘学报, 2017, 46(1): 1-8. |
| [5] |
杨元喜. 综合PNT体系及其关键技术[J]. 测绘学报, 2016, 45(5): 505-510. |
| [6] |
SPIESS F N. Analysis of a possible sea floor strain measurement system[J]. Marine Geodesy, 1985, 9(4): 385-398. DOI:10.1080/15210608509379536 |
| [7] |
李林阳, 吕志平, 崔阳. 海底大地测量控制网研究进展综述[J]. 测绘通报, 2018(1): 8-13. DOI:10.13474/j.cnki.11-2246.2018.0002 |
| [8] |
辛明真. 基于GNSS-A浮标的水下非差定位关键技术研究[D]. 青岛: 山东科技大学, 2016.
|
| [9] |
赵建虎, 梁文彪. 海底控制网测量和解算中的几个关键问题[J]. 测绘学报, 2019, 48(9): 1197-1202. |
| [10] |
HONSHO C, KIDO M, TOMITA F, et al. Offshore postseismic deformation of the 2011 Tohoku Earthquake Revisited: Application of an improved GPS-acoustic positioning method considering horizontal gradient of sound speed structure[J]. Journal of Geophysical Research: Solid Earth, 2019, 124(6): 5990-6009. DOI:10.1029/2018JB017135 |
| [11] |
CHADWELL C D, SPIESS F N. Plate motion at the ridge-transform boundary of the south Cleft segment of the Juan de Fuca Ridge from GPS-acoustic data[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B4): B04415. DOI:10.1029/2007JB004936 |
| [12] |
IKUTA R, TADOKORO K, ANDO M. A new GPS-acoustic method for measuring ocean floor crustal deformation: Application to the Nankai Trough[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B2): B02401. DOI:10.1029/2006JB004875 |
| [13] |
BALLU V, BOUIN M N, CALMANT S, et al. Absolute seafloor vertical positioning using combined pressure gauge and kinematic GPS data[J]. Journal of Geodesy, 2010, 84(1): 65-77. DOI:10.1007/s00190-009-0345-y |
| [14] |
杨元喜, 刘焱雄, 孙大军, 等. 海底大地基准网建设及其关键技术[J]. 中国科学(地球科学), 2020, 50(7): 936-945. |
| [15] |
KINUGASA N, TADOKORO K, KATO T, et al. Estimation of temporal and spatial variation of sound speed in ocean from GNSS-A measurements for observation using moored buoy[J]. Progress in Earth and Planetary Science, 2020, 7(1): 21. DOI:10.1186/s40645-020-00331-5 |
| [16] |
单瑞, 董凌宇, 杜凯, 等. 超短基线定位系统在深拖探测中的应用[J]. 海洋地质前沿, 2019, 35(9): 29-35. |
| [17] |
XU P L, ANDO M, TADOKORO K. Precise three-dimensional seafloor geodetic deformation measurements using difference techniques[J]. Earth Planets and Space, 2005, 57(9): 795-808. DOI:10.1186/BF03351859 |
| [18] |
孙文舟, 殷晓冬, 暴景阳, 等. 海底控制点定位的半参数平差模型法[J]. 测绘学报, 2019, 48(1): 117-123. |
| [19] |
FUJITA M, ISHIKAWA T, MOCHIZUKI M, et al. GPS/Acoustic seafloor geodetic observation: Method of data analysis and its application[J]. Earth, Planets and Space, 2006, 58(3): 265-275. DOI:10.1186/BF03351923 |
| [20] |
ZHAO S, WANG Z J, HE K F, et al. Investigation on underwater positioning stochastic model based on acoustic ray incidence angle[J]. Applied Ocean Research, 2018, 77: 69-77. DOI:10.1016/j.apor.2018.05.011 |
| [21] |
邝英才, 吕志平, 王方超, 等. GNSS/声学联合定位的自适应滤波算法[J]. 测绘学报, 2020, 49(7): 854-864. |
| [22] |
ZHAO S, WANG Z J, NIE Z X, et al. Investigation on total adjustment of the transducer and seafloor transponder for GNSS/Acoustic precise underwater point positioning[J]. Ocean Engineering, 2021, 221: 108533. DOI:10.1016/j.oceaneng.2020.108533 |
| [23] |
赵建虎, 邹亚靖, 吴永亭, 等. 深度约束的海底控制网点坐标确定方法[J]. 哈尔滨工业大学学报, 2016, 48(10): 137-141. DOI:10.11918/j.issn.0367-6234.2016.10.020 |
| [24] |
孙大军, 郑翠娥, 张居成, 等. 水声定位导航技术的发展与展望[J]. 中国科学院院刊, 2019, 34(3): 331-338. |
| [25] |
CHEN G X, LIU Y, LIU Y X, et al. Improving GNSS-acoustic positioning by optimizing the ship's track lines and observation combinations[J]. Journal of Geodesy, 2020, 94(6): 61. DOI:10.1007/s00190-020-01389-1 |
| [26] |
ZHANG T, CHEN L P, LI Y. AUV underwater positioning algorithm based on interactive assistance of SINS and LBL[J]. Sensors, 2015, 16(1): 42. DOI:10.3390/s16010042 |
| [27] |
王振杰, 刘慧敏, 单瑞, 等. 顾及系统噪声和观测噪声的分级自适应信息滤波算法[J]. 武汉大学学报(信息科学版), 2021, 46(1): 88-95. |
| [28] |
SATO M, FUJITA M, MATSUMOTO Y, et al. Improvement of GPS/acoustic seafloor positioning precision through controlling the ship's track line[J]. Journal of Geodesy, 2013, 87(9): 825-842. |
| [29] |
TOMITA F, KIDO M, HONSHO C, et al. Development of a kinematic GNSS-Acoustic positioning method based on a state-space model[J]. Earth, Planets and Space, 2019, 71(1): 102. DOI:10.1186/s40623-019-1082-y |
| [30] |
CHEN H H, WANG C C. Optimal localization of a seafloor transponder in shallow water using acoustic ranging and GPS observations[J]. Ocean Engineering, 2007, 34(17/18): 2385-2399. |
| [31] |
刘慧敏, 王振杰, 赵爽. 深度约束的浅海多目标声学定位方法[J]. 石油地球物理勘探, 2019, 54(6): 1181-1187. |
| [32] |
CHEN H H, WANG C C. Accuracy assessment of GPS/Acoustic positioning using a Seafloor Acoustic Transponder System[J]. Ocean Engineering, 2011, 38(13): 1472-1479. |
| [33] |
刘慧敏, 王振杰, 吴绍玉, 等. 顾及声线弯曲的浅海多目标水声定位算法[J]. 石油地球物理勘探, 2019, 54(1): 9-15. |
| [34] |
王振杰, 刘慧敏, 杨慧良, 等. 基于垂直约束的深海拖曳系统USBL/DVL组合导航算法[J]. 中国惯性技术学报, 2019, 27(5): 670-676. |
| [35] |
BATISTA P, SILVESTRE C, OLIVEIRA P. A sensor-based Long Baseline position and velocity navigation filter for underwater vehicles[J]. IFAC Proceedings Volumes, 2010, 43(14): 302-307. |
| [36] |
陆秀平, 边少锋, 黄谟涛, 等. 常梯度声线跟踪中平均声速的改进算法[J]. 武汉大学学报(信息科学版), 2012, 37(5): 590-593. |
| [37] |
SAKIC P, BALLU V, CRAWFORD W C, et al. Acoustic ray tracing comparisons in the context of geodetic precise off-shore positioning experiments[J]. Marine Geodesy, 2018, 41(4): 315-330. |
| [38] |
赵建虎, 陈鑫华, 吴永亭, 等. 顾及波浪影响和深度约束的水下控制网点绝对坐标的精确确定[J]. 测绘学报, 2018, 47(3): 413-421. |



